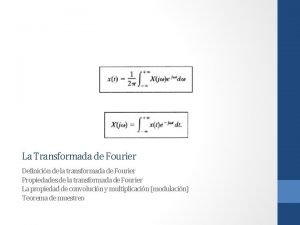
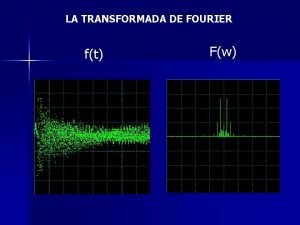
Transformada de Fourier TF Aula Terica Semana 15

Transformada de Fourier (TF) Aula Teórica – Semana 15 PC - Prof. RCBetini 1

Transformada de Fourier • Os sinais podem ser divididos em categorias diferentes conforme mostra a tabela abaixo. • Dependendo do tipo de sinal pode-se utilizar a Série ou a Transformada de Fourier para fins de análise espectral. Tipos de Sinais PC - Prof. RCBetini 2

Série de Fourier • Utilizada na análise de sinais periódicos. • A Série de Fourier é subdividida com base na teoria dos números complexos, em trigonométrica ou exponencial. • A trigonométrica fornece um espectro unilateral (só frequências positivas). • A Série Exponencial fornece um espectro bilateral (frequências positivas e negativas) PC - Prof. RCBetini 3

Série de Fourier Trigonométrica (Espectro Unilateral) • Um sinal periódico x(t) pode ser definido por uma soma de funções senoidais e cosenoidais, como mostrado abaixo. PC - Prof. RCBetini 4

Série de Fourier Trigonométrica (Espectro Unilateral) • Para sinais pares, ou seja, quando x(t)=x(-t), a série pode ser reduzida para. • E quando o sinal é ímpar, com x(t)=-x(-t), a série pode ser reduzida a PC - Prof. RCBetini 5

Série de Fourier Exponencial (Espectro Bilateral) • Apresenta como grande vantagem o cálculo de apenas uma integral. PC - Prof. RCBetini 6

Série de Fourier Exponencial (Espectro Bilateral) • Como visto anteriormente, a função exponencial pode ser decomposta em “cos + jsen”. • Para funções pares, a integral pode ser feita exclusivamente em função do co-seno enquanto que, para funções ímpares, pode ser feita em função do seno. • Antes de demonstrar o cálculo de algumas séries, vamos definir a função “sinc” PC - Prof. RCBetini 7

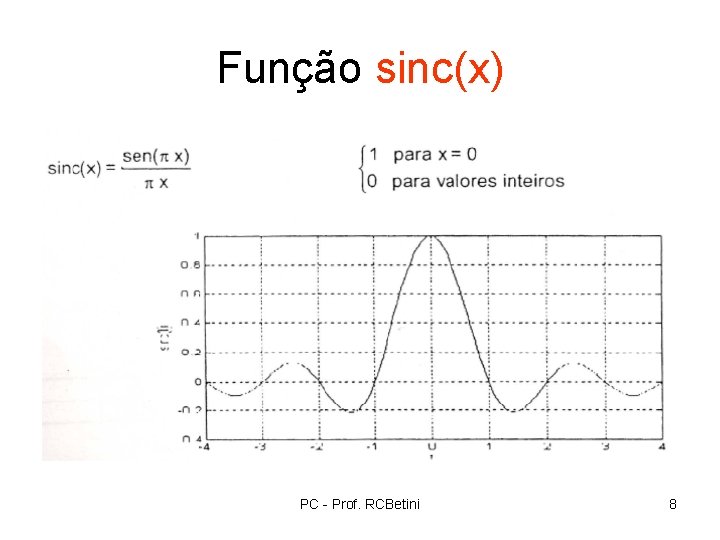
Função sinc(x) PC - Prof. RCBetini 8

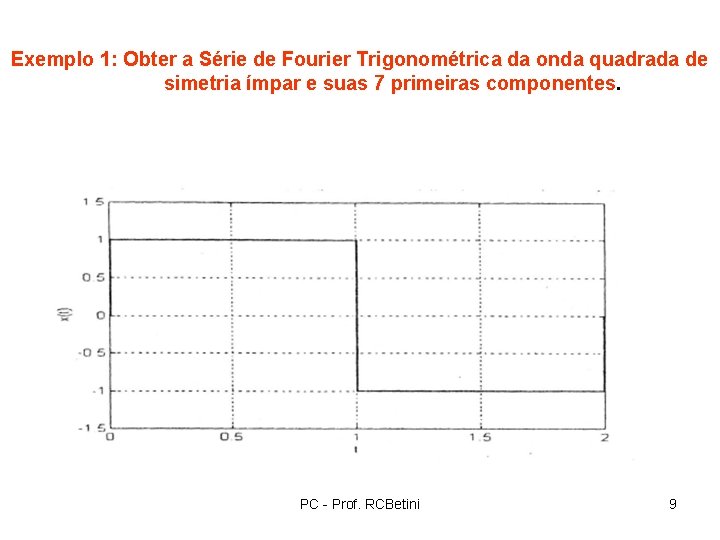
Exemplo 1: Obter a Série de Fourier Trigonométrica da onda quadrada de simetria ímpar e suas 7 primeiras componentes. PC - Prof. RCBetini 9

PC - Prof. RCBetini 10

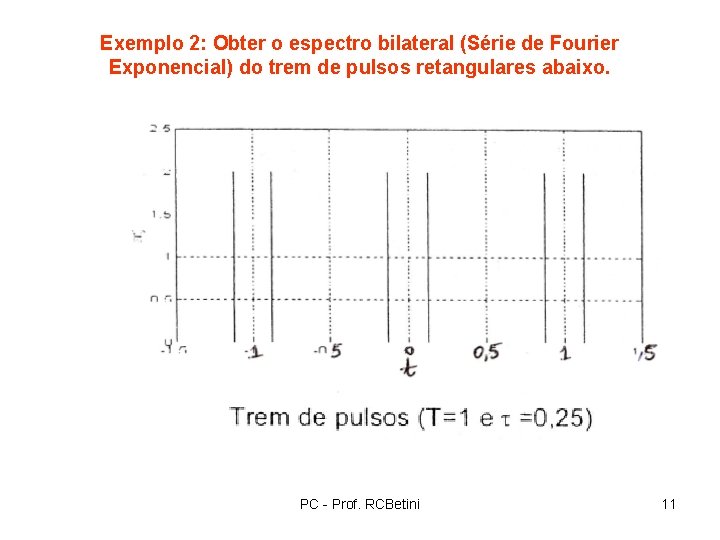
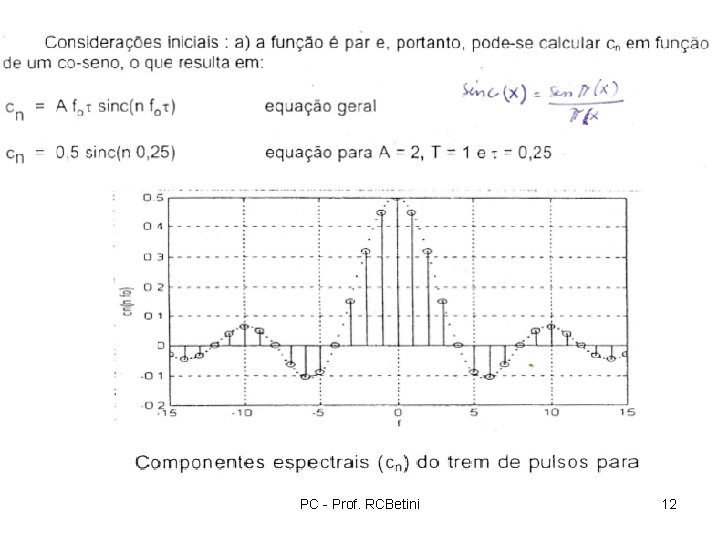
Exemplo 2: Obter o espectro bilateral (Série de Fourier Exponencial) do trem de pulsos retangulares abaixo. PC - Prof. RCBetini 11

PC - Prof. RCBetini 12

Exemplo 3: • Neste exemplo é demonstrado a aplicação da Série de Fourier a um circuito RL, o qual causará variações de amplitude e fase nas componentes, filtrando assim o sinal de entrada. • Para isto, considere-se um circuito RL tipo série, onde R=1 e L=0, 5 H, sobre o qual é aplicado um sinal v(t) tipo triangular, que é definido por uma série infinita. • Determinar i(t) e ambas as formas de onda, considerando-se apenas as 7 primeiras componentes (“n” variando de 1 a 7). PC - Prof. RCBetini 13

PC - Prof. RCBetini 14

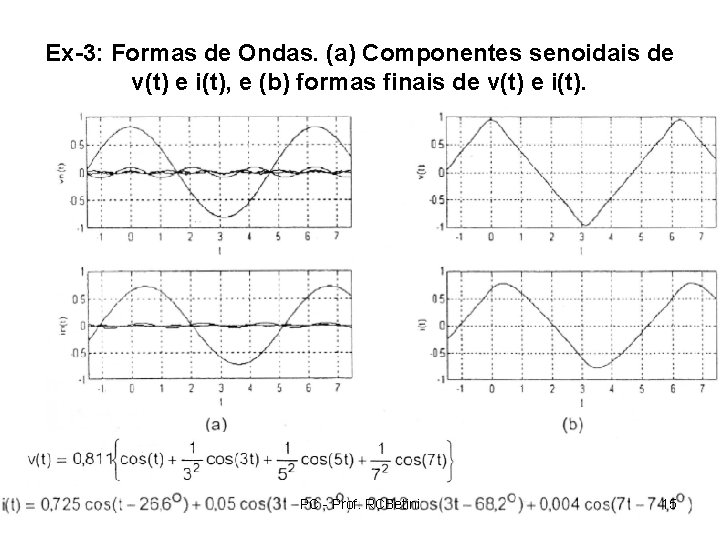
Ex-3: Formas de Ondas. (a) Componentes senoidais de v(t) e i(t), e (b) formas finais de v(t) e i(t). PC - Prof. RCBetini 15

Exercício-3: Considerações. • A corrente i(t) está atrasada em relação a tensão v(t), confirmando que o indutor se opõe a variações de corrente. • A corrente i(t) tem uma forma de onda mais suave, o que implica que, se a tensão de saída for obtida sobre o resistor, obter-se á um sinal com a mesma forma de onda. Neste caso o sinal de entrada terá passado por um filtro passabaixas, enquanto que, se for obtida sobre o indutor, terá passado por um filtro passa-altas. PC - Prof. RCBetini 16

Transformada de Fourier PC - Prof. RCBetini 17

Transformada de Fourier PC - Prof. RCBetini 18

Transformada de Fourier • Obter as respectivas TF das funções retângulo, triângulo e impulso. PC - Prof. RCBetini 19

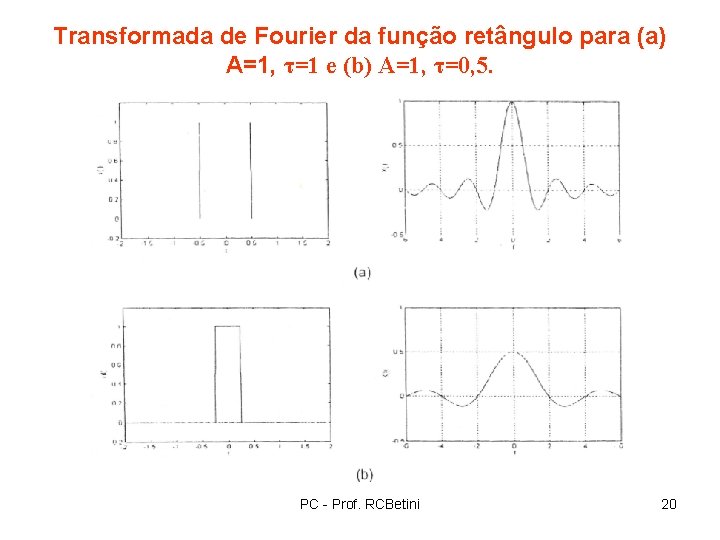
Transformada de Fourier da função retângulo para (a) A=1, τ=1 e (b) A=1, τ=0, 5. PC - Prof. RCBetini 20

PC - Prof. RCBetini 21

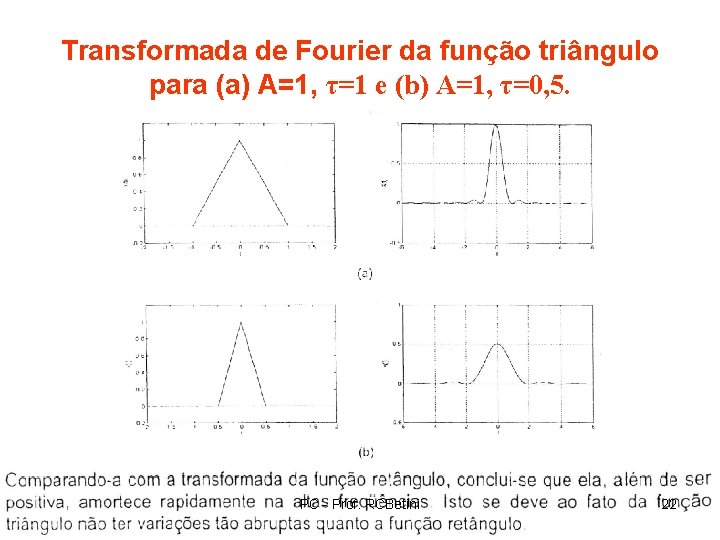
Transformada de Fourier da função triângulo para (a) A=1, τ=1 e (b) A=1, τ=0, 5. PC - Prof. RCBetini 22

PC - Prof. RCBetini 23

PC - Prof. RCBetini 24