Transferring Instances for ModelBased Reinforcement Learning Matthew E

Transferring Instances for Model-Based Reinforcement Learning Matthew E. Taylor Teamcore Department of Computer Science University of Southern California Joint work with Nicholas K. Jong, and Peter Stone Learning Agents Research Group Department of Computer Sciences University of Texas at Austin

Inter-Task Transfer • Learning tabula rasa can be unnecessarily slow • Humans can use past information – – • Soccer with different numbers of players Different state variables and actions Agents: leverage learned knowledge in novel/modified tasks 1. 2. Learn faster Larger and more complex problems become tractable Matthew E. Taylor 2

Model-Based RL vs. Model-Free RL • Model Free 140 Visited State Distribution 120 – Q-Learning, Sarsa, etc. – Learn values of actions – In example: ~256 actions 100 80 Random Exploration With Planning 60 40 20 20 00 00 Start • Model-Based 22 44 State Number 66 88 Goal Action 1: Return to Start Action 2: Move to Right Reward: +1 at Goal, 0 otherwise – Dyna-Q, R-Max, etc. – Learn effects of actions (“what is the next state? ” → planning) – In example: ~36 actions Matthew E. Taylor 3

TIMBREL Transferring Instances for Model Based REinforcement Learning • Transfer between – Model-learning RL algorithms – Different state variables and actions – Continuous state spaces n. An ancient percussion instrument similar to a tambourine. • In this paper, we use: – Fitted R-Max [Jong and Stone, 2007] – Generalized mountain car domain Matthew E. Taylor 4

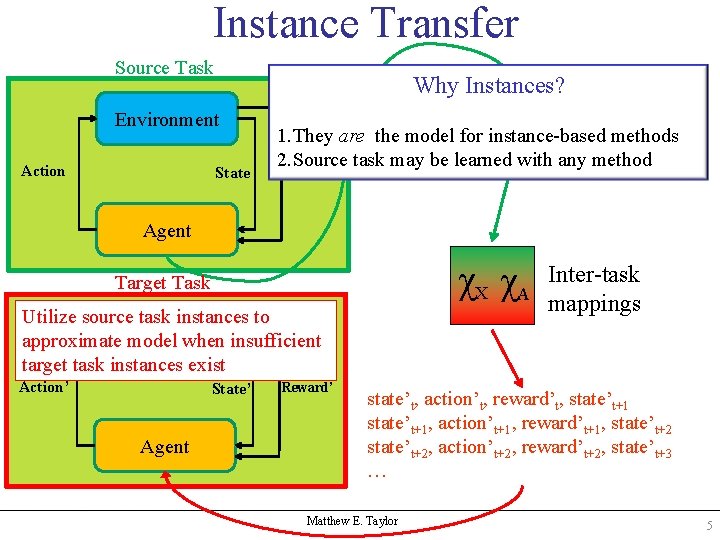
Instance Transfer Source Task Environment Action State statet, Why action. Instances? t, rewardt, statet+1, actiont+1, rewardt+1, statet+2 1. They are state the model for instance-based methods t+2, actiont+2, rewardt+2, statet+3 2. Source task … may be learned with any method Reward Agent χX χA Target Task Utilize source task instances to approximate. Environment model when insufficient target task instances exist Action’ State’ Agent Reward’ Inter-task mappings state’t, action’t, reward’t, state’t+1, action’t+1, reward’t+1, state’t+2, action’t+2, reward’t+2, state’t+3 … Matthew E. Taylor 5

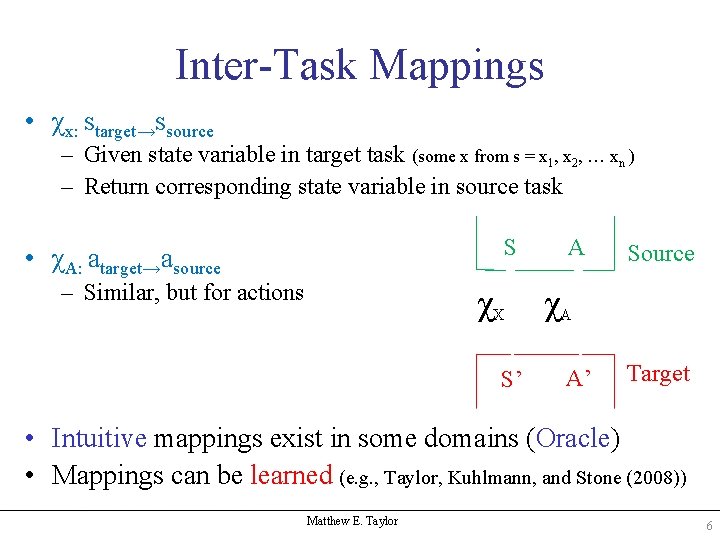
Inter-Task Mappings • χx: starget→ssource – Given state variable in target task (some x from s = x 1, x 2, … xn ) – Return corresponding state variable in source task S • χA: atarget→asource – Similar, but for actions χX S’ A Source χA A’ Target • Intuitive mappings exist in some domains (Oracle) • Mappings can be learned (e. g. , Taylor, Kuhlmann, and Stone (2008)) Matthew E. Taylor 6

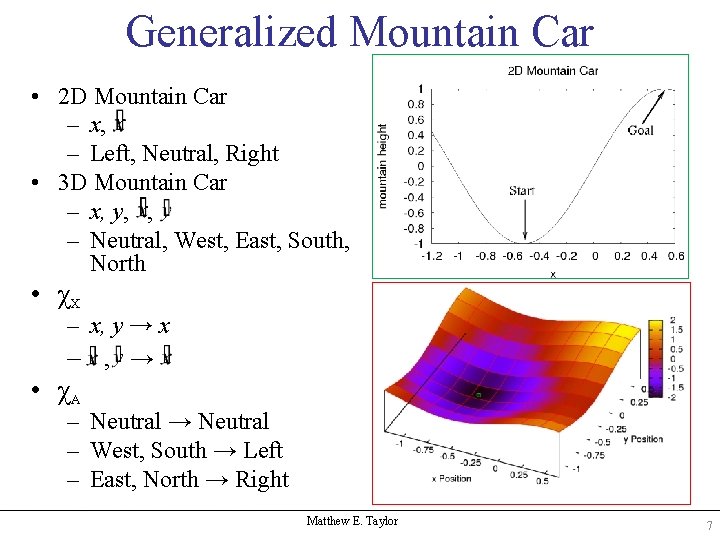
Generalized Mountain Car • 2 D Mountain Car – x, – Left, Neutral, Right • 3 D Mountain Car – x, y, , – Neutral, West, East, South, North • χX – x, y → x – , → • χA – Neutral → Neutral – West, South → Left – East, North → Right Matthew E. Taylor 7

Fitted R-Max [Jong and Stone, 2007] • • Instance-based RL method [Ormoneit & Sen, 2002] Handles continuous state spaces Weights recorded transitions by distances Plans over discrete, abstract MDP Example: 2 state variables, 1 action y ? x Matthew E. Taylor 8

Fitted R-Max [Jong and Stone, 2007] • • Instance-based RL method [Ormoneit & Sen, 2002] Handles continuous state spaces Weights recorded transitions by distances Plans over discrete, abstract MDP Example: 2 state variables, 1 action y x Matthew E. Taylor 9

Fitted R-Max [Jong and Stone, 2007] • • Instance-based RL method [Ormoneit & Sen, 2002] Handles continuous state spaces Weights recorded transitions by distances Plans over discrete, abstract MDP Example: 2 state variables, 1 action y x Matthew E. Taylor 10

Fitted R-Max [Jong and Stone, 2007] • • Instance-based RL method [Ormoneit & Sen, 2002] Handles continuous state spaces Weights recorded transitions by distances Plans over discrete, abstract MDP Example: 2 state variables, 1 action y Utilize source task instances to approximate model when insufficient target task instances exist x Matthew E. Taylor 11

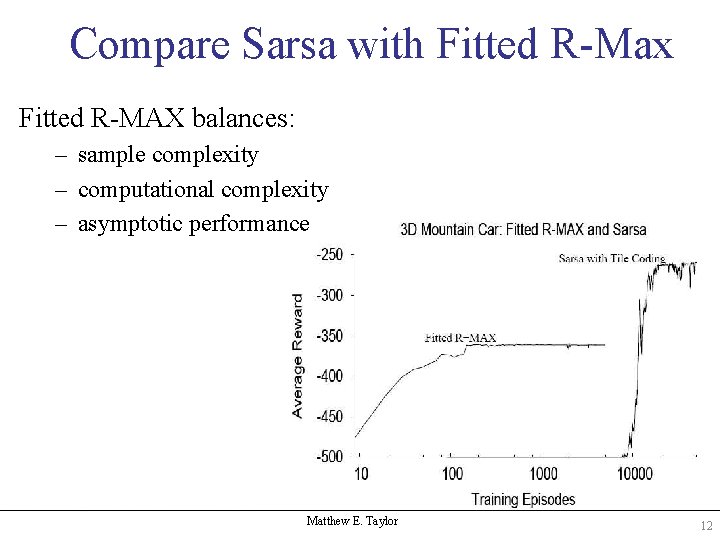
Compare Sarsa with Fitted R-Max Fitted R-MAX balances: – sample complexity – computational complexity – asymptotic performance Matthew E. Taylor 12

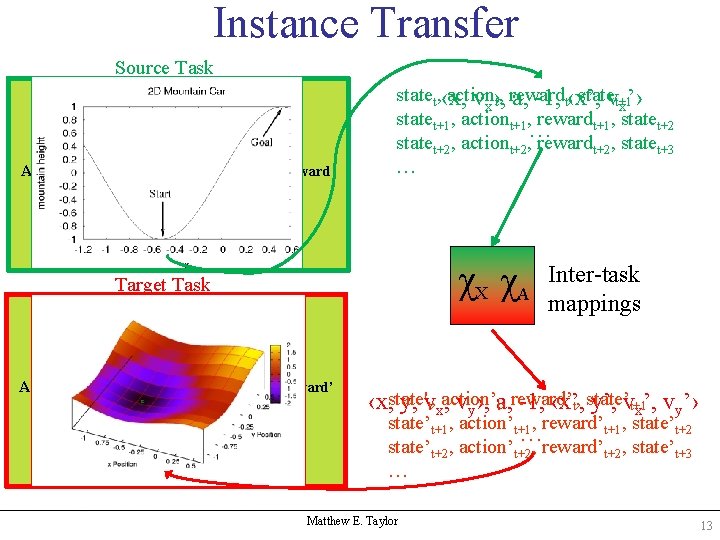
Instance Transfer Source Task Environment Action State Reward statet, ‹x, action , statevt+1 vx›, t, reward a, -1, t‹x’, x’› statet+1, actiont+1, rewardt+1, statet+2 … statet+2, actiont+2, rewardt+2, statet+3 … Agent χX χA Target Task Inter-task mappings Environment Action’ State’ Agent Reward’ ‹x, state' y, vt, xaction’ , vy›, a, -1, ‹x’, t, state’ y’, vt+1 t, reward’ x’, vy’› state’t+1, action’t+1, reward’t+1, state’t+2 … state’t+2, action’t+2, reward’t+2, state’t+3 … Matthew E. Taylor 13

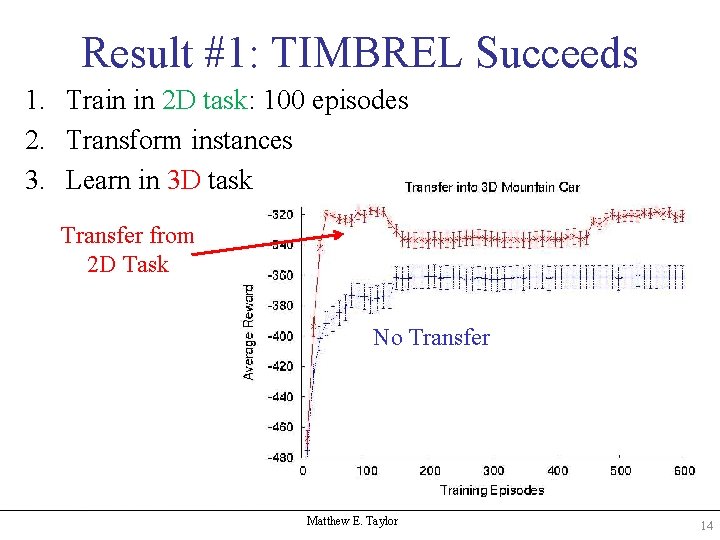
Result #1: TIMBREL Succeeds 1. Train in 2 D task: 100 episodes 2. Transform instances 3. Learn in 3 D task Transfer from 2 D Task No Transfer Matthew E. Taylor 14

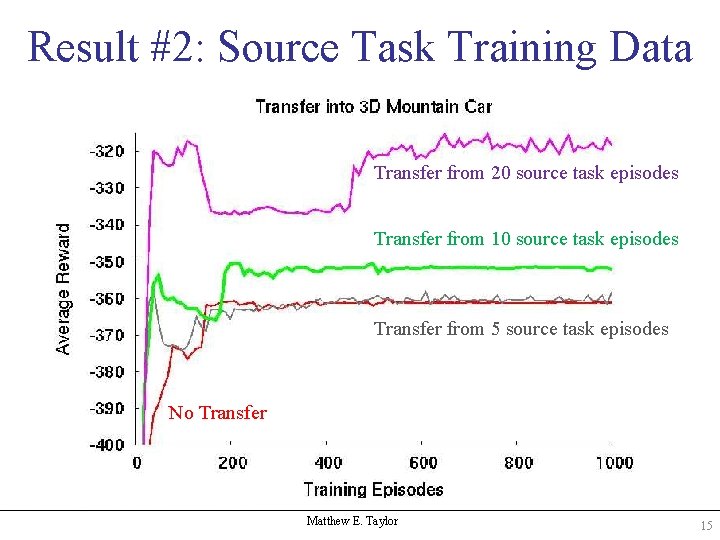
Result #2: Source Task Training Data Transfer from 20 source task episodes Transfer from 10 source task episodes Transfer from 5 source task episodes No Transfer Matthew E. Taylor 15

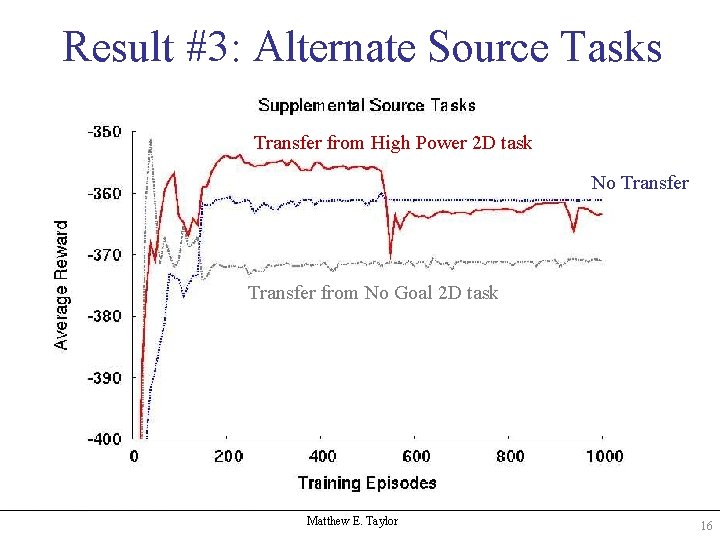
Result #3: Alternate Source Tasks Transfer from High Power 2 D task No Transfer from No Goal 2 D task Matthew E. Taylor 16

Selected Related Work • Instance Transfer in Fitted Q Iteration – • Lazaric et. al, 2008 Transferring Regression Model of Transition Function – • Atkeson and Santamaria, 1997 Ordering Prioritized Sweeping via Transfer – • Sunmola and Wyatt, 2006 Bayesian Model Transfer – – Tanaka and Yamamura, 2003 Wilson et. al, 2007 Matthew E. Taylor 17

Future Work • Implement with other model-learning methods – Dyna-Q Discrete tasks only – R-Max – Fitted Q Iteration • Guard against U-shaped curve in Fitted R-Max? • Examine more complex tasks – Can TIMBREL improve performance of real world problems? Matthew E. Taylor 18

TIMBREL Conclusions • • Significantly increases speed of learning Results suggest less data needed to learn than – – – • Model-based RL without transfer Model-free RL with transfer Transfer performances depends on: – – Source task and target task similarity Amount of source task data collected Matthew E. Taylor 19