Transfer Matrix Method In Solving EM Yaoxuan Li

Transfer Matrix Method In Solving EM Yaoxuan Li , Weijia Wang , Shaojie Ma Problem Produced by Presented by Y. X. Li

OUTLINE 1 Introducing Transfer Matrix in Solving Laplace Equation 2 General Properties for TMM in Multi-layer Shell 3 General use in EM Wave Propagating in Multi-layer

1 Introducing Transfer Matrix in Solving Laplace Equation 2 General Properties for TMM in Multi-layer Shell 3 General use in EM Wave Propagating in Multi-layer

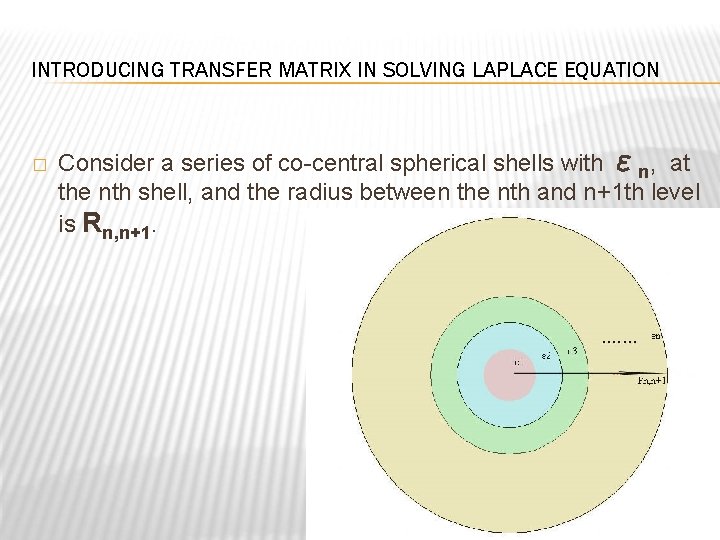
INTRODUCING TRANSFER MATRIX IN SOLVING LAPLACE EQUATION � Consider a series of co-central spherical shells with εn, at the nth shell, and the radius between the nth and n+1 th level is Rn, n+1.

INTRODUCING TRANSFER MATRIX IN SOLVING LAPLACE EQUATION � We see a simple example first. We apply a uniform field E=E 0 ex , and then solve the Laplace equation in the spherical coordinate, we got solutions for the 1 st order inducing field and boundary conditions , at r = Rn 1, n

INTRODUCING TRANSFER MATRIX IN SOLVING LAPLACE EQUATION � Then we would easily manifest An and Bn in terms of An-1 and Bn-1 as

INTRODUCING TRANSFER MATRIX IN SOLVING LAPLACE EQUATION � and further in matrix form where

INTRODUCING TRANSFER MATRIX IN SOLVING LAPLACE EQUATION � The matrix the is called the transfer matrix for n-1, n th level. If at the 1 st level there is A 1 and B 1=0( to ensure converge) and at the infinite space there is An= -E 0 and Bn, multiply the transfer matrix again and again we will get And surly we got the solution of A 1 and Bn, then whichever Ak and Bk you want could be solved by using transfer matrix.

1 Introducing Transfer Matrix in Solving Laplace Equation 2 General Properties for TMM in Multi-layer Shell 3 General use in EM Wave Propagating in Multi-layer

GENERAL PROPERTIES FOR TMM IN MULTI-LAYER SHELL � We now start some general solution for general conditions, solutions to be we apply the same B. C and trick in calculation

GENERAL PROPERTIES FOR TMM IN MULTI-LAYER SHELL � the TMM notation will be and elements when l=1, the results would automatically turn to the same results in the previous story.

GENERAL PROPERTIES FOR TMM IN MULTI-LAYER SHELL � Furthermore, when adding up free boundary charge, the boundary condition will turn to be we will soon get a solution no more complex than before where But the additional term, called charge term, is not that neat.

GENERAL PROPERTIES FOR TMM IN MULTI-LAYER SHELL � Though tough, but physics For a metal layer, the potential is constant, therefore only , otherwise is 0. If in the boundary for n, n+1 th layer there is a l order charge , we would directly got It means, the surface charge density is just like other external conditions such as E field, would only induce the same order term, as a uniform E inducing only a term.

1 Introducing Transfer Matrix in Solving Laplace Equation 2 General Properties for TMM in Multi-layer Shell 3 General use in EM Wave Propagating in Multi-layer

GENERAL USE IN EM WAVE PROPAGATING IN MULTI-LAYER � Consider a multi-layer withεn in the nth layer, and position of the boundary between nth and n+1 th is dn, n+1 along z direction. Assume the wave propagates along z direction, perpendicular to the layer, with the expression of field, where Solve , we got As we have assumed there is not any surface current, so the boundary conditions are

GENERAL USE IN EM WAVE PROPAGATING IN MULTI-LAYER � Then got the solution Simply we can change the expression into matrix

GENERAL USE IN EM WAVE PROPAGATING IN MULTI-LAYER � and in it, we define If there are n layer (noticing that outside the layers are air, so the 0 th and n+1 th layer are absolutely air terms), the final solution can be written as

GENERAL USE IN EM WAVE PROPAGATING IN MULTI-LAYER � Further if we define the starting terms as , the solution could be simplified to the transfer matrix By using this method we could quickly get the answer of t and r And from this we could use transfer method to get the propagating properties in any layers.

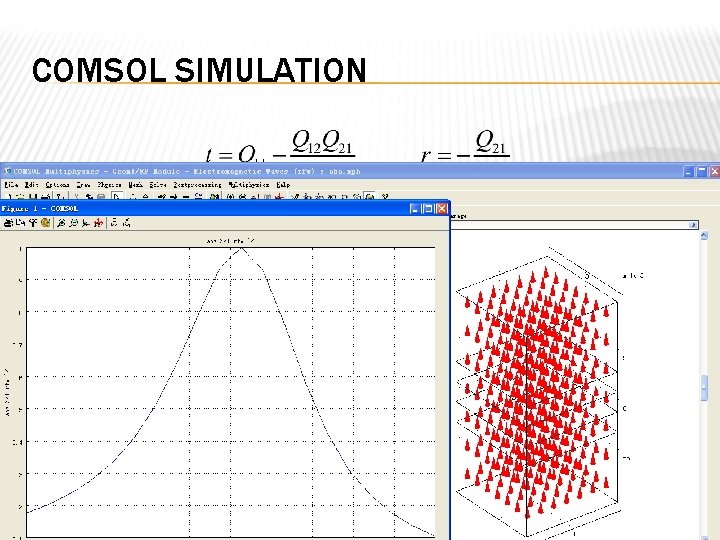
COMSOL SIMULATION � � Interestingly, from the result above, one could think that, if Q 21= 0, the reflective terms would be 0, and further if Q 11= 1, meaning no absorption, t=1 , the transmittance behavior would be perfect. Specifically, we could input some data asε 1=1000, ε 2= 2000, d 1=d 2= 2 mm, then we get ω= 2π*0. 850 GHz, there is a perfect transmission. From a COMSOL simulation we can see the S 21 is near to 1.