Transfer Learning Algorithms for Image Classification Ariadna Quattoni

Transfer Learning Algorithms for Image Classification Ariadna Quattoni MIT, CSAIL Advisors: Michael Collins Trevor Darrell 1

Motivation Goal: q We want to be able to build classifiers for thousands of visual categories. q We want to exploit rich and complex feature representations. Problem: q We might only have a few labeled samples per category. Solution: q Transfer Learning, leverage labeled data from multiple related tasks. 2 / 46

Thesis Contributions We study efficient transfer algorithms for image classification which can exploit supervised training data from a set of related tasks: q Learn an image representation using supervised data from auxiliary tasks automatically derived from unlabeled images + meta-data. q A transfer learning model based on joint regularization and an efficient optimization algorithm for training jointly sparse classifiers in high dimensional feature spaces. 3 / 46

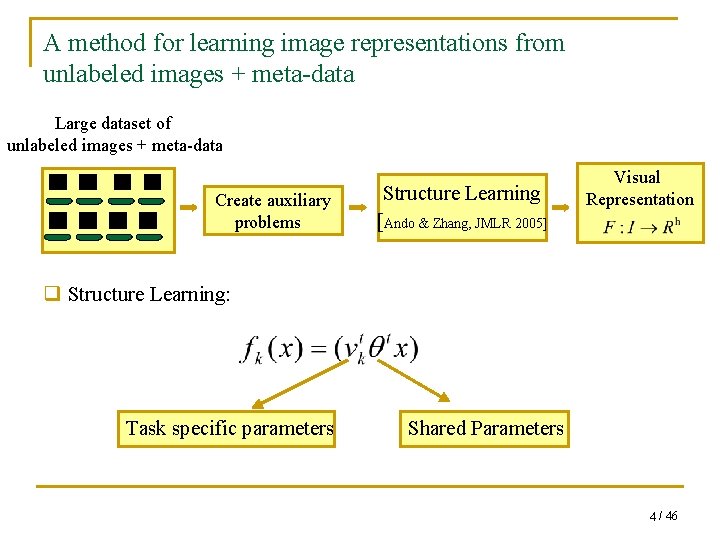
A method for learning image representations from unlabeled images + meta-data Large dataset of unlabeled images + meta-data Create auxiliary problems Structure Learning [Ando & Zhang, JMLR 2005] Visual Representation q Structure Learning: Task specific parameters Shared Parameters 4 / 46

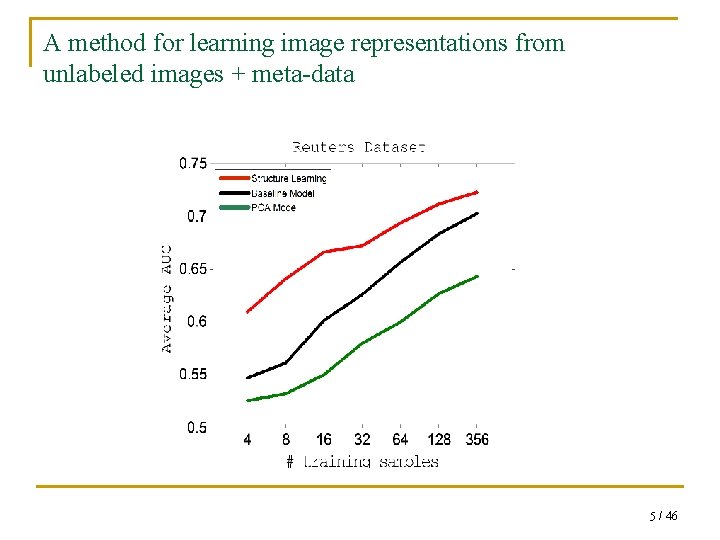
A method for learning image representations from unlabeled images + meta-data 5 / 46

Outline q An overview of transfer learning methods. q. A joint sparse approximation model for transfer learning. q. Asymmetric transfer experiments. q. An efficient training algorithm. q. Symmetric transfer image annotation experiments. 6 / 46

Transfer Learning: A brief overview q The goal of transfer learning is to use labeled data from related tasks to make learning easier. Two settings: § Asymmetric transfer: Resource: Large amounts of supervised data for a set of related tasks. Goal: Improve performance on a target task for which training data is scarce. § Symmetric transfer: Resource: Small amount of training data for a large number of related tasks. Goal: Improve average performance over all classifiers. 7 / 46

Transfer Learning: A brief overview q Three main approaches: q Learning intermediate latent representations: [Thrun 1996, Baxter 1997, Caruana 1997, Argyriou 2006, Amit 2007] q Learning priors over parameters: [Raina 2006, Lawrence et al. 2004 ] q Learning relevant shared features [Torralba 2004, Obozinsky 2006] 8 / 46

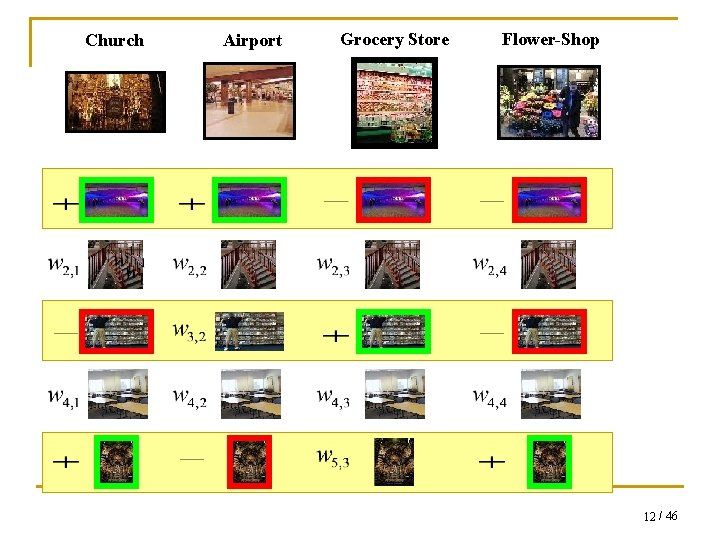
Feature Sharing Framework: q Work with a rich representation: q Complex features, high dimensional space q Some of them will be very discriminative (hopefully) q Most will be irrelevant q Related problems may share relevant features. q If we knew the relevant features we could: q Learn from fewer examples q Build more efficient classifiers q We can train classifiers from related problems together using a regularization penalty designed to promote joint sparsity. 9 / 46

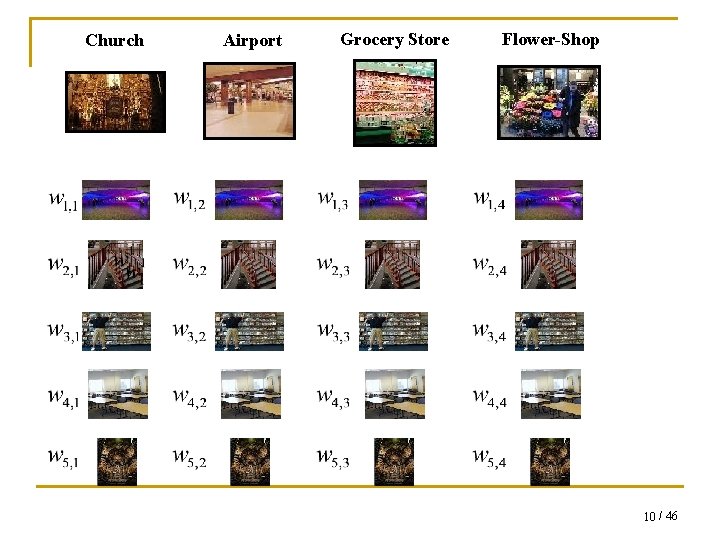
Church Airport Grocery Store Flower-Shop 10 / 46

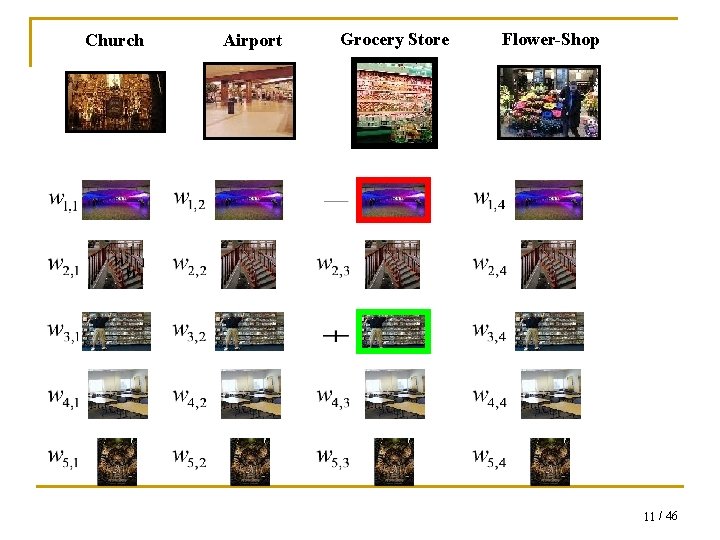
Church Airport Grocery Store Flower-Shop 11 / 46

Church Airport Grocery Store Flower-Shop 12 / 46

Related Formulations of Joint Sparse Approximation q Torralba et al. [2004] developed a joint boosting algorithm based on the idea of learning additive models for each class that share weak learners. q Obozinski et al. [2006] proposed L 1 -2 joint penalty and developed a blockwise boosting scheme based on Boosted-Lasso. 13 / 46

Our Contribution A new model and optimization algorithm for training jointly sparse classifiers: q Previous approaches to joint sparse approximation have relied on greedy coordinate descent methods. q We propose a simple an efficient global optimization algorithm with guaranteed convergence rates. q Our algorithm can scale to large problems involving hundreds of problems and thousands of examples and features. q We test our model on real image classification tasks where we observe improvements in both asymmetric and symmetric transfer settings. 14 / 46

Outline q An overview of transfer learning methods. q A joint sparse approximation model for transfer learning. q Asymmetric transfer experiments. q An efficient training algorithm. q Symmetric transfer image annotation experiments. 15 / 46

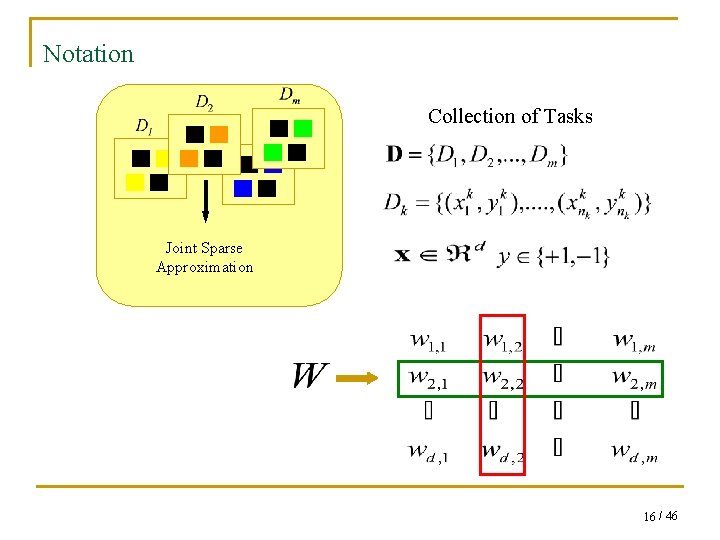
Notation Collection of Tasks Joint Sparse Approximation 16 / 46

Single Task Sparse Approximation q Consider learning a single sparse linear classifier of the form: q We want a few features with non-zero coefficients q Recent work suggests to use L 1 regularization: Classification error L 1 penalizes non-sparse solutions q Donoho [2004] proved (in a regression setting) that the solution with smallest L 1 norm is also the sparsest solution. 17 / 46

Joint Sparse Approximation q Setting : Joint Sparse Approximation Average Loss on Collection D Penalizes solutions that utilize too many features 18 / 46

Joint Regularization Penalty q How do we penalize solutions that use too many features? Coefficients for feature 2 Coefficients for classifier 2 q Would lead to a hard combinatorial problem. 19 / 46

Joint Regularization Penalty q We will use a L 1 -∞ norm [Tropp 2006] q This norm combines: The L∞ norm on each row promotes nonsparsity on each row. An L 1 norm on the maximum absolute values of the coefficients across tasks promotes sparsity. Share features Use few features q The combination of the two norms results in a solution where only a few features are used but the features used will contribute in solving many classification problems. 20 / 46

Joint Sparse Approximation q Using the L 1 -∞ norm we can rewrite our objective function as: q For any convex loss this is a convex objective. q For the hinge loss: the optimization problem can be expressed as a linear program. 21 / 46

Joint Sparse Approximation q Linear program formulation (hinge loss): q Objective: q Max value constraints: and q Slack variables constraints: and 22 / 46

Outline q An overview of transfer learning methods. q A joint sparse approximation model for transfer learning. q Asymmetric transfer experiments. q An efficient training algorithm. q Symmetric transfer image annotation experiments. 23 / 46

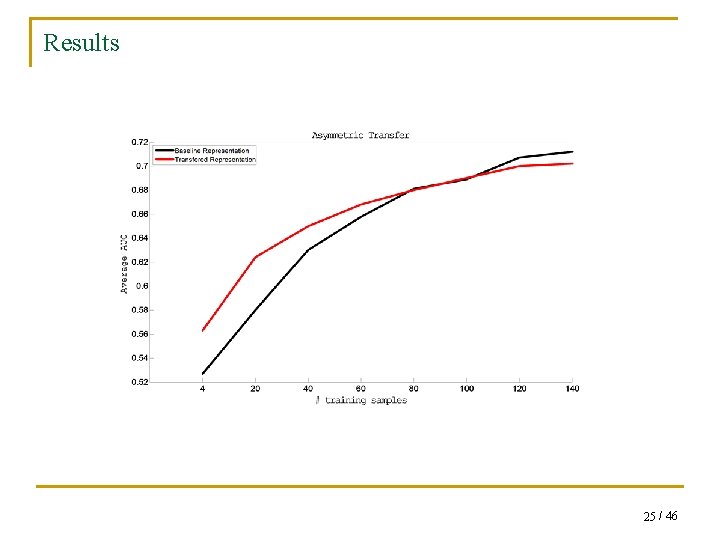
Setting: Asymmetric Transfer Super. Bowl Sharon Danish Cartoons Academy Awards Australian Open Grammys Trapped Miners Figure Skating Golden globes Iraq q Train a classifier for the 10 th held out topic using the relevant features R only. q Learn a representation using labeled data from 9 topics. q Learn the matrix W using our transfer algorithm. q Define the set of relevant features to be: 24 / 46

Results 25 / 46

Outline q An overview of transfer learning methods. q A joint sparse approximation model for transfer learning. q Asymmetric transfer experiments. q An efficient training algorithm. q Symmetric transfer image annotation experiments. 26 / 46

Limitations of the LP formulation q The LP formulation can be optimized using standard LP solvers. q The LP formulation is feasible for small problems but becomes intractable for larger data-sets with thousands of examples and dimensions. q We might want a more general optimization algorithm that can handle arbitrary convex losses. 27 / 46

L 1 -∞ Regularization: Constrained Convex Optimization Formulation A convex function Convex constraints q We will use a Projected Sub. Gradient method. Main advantages: simple, scalable, guaranteed convergence rates. q Projected Sub. Gradient methods have been recently proposed: q L 2 regularization, i. e. SVM [Shalev-Shwartz et al. 2007] q L 1 regularization [Duchi et al. 2008] 28 / 46

Euclidean Projection into the L 1 -∞ ball 29 / 46

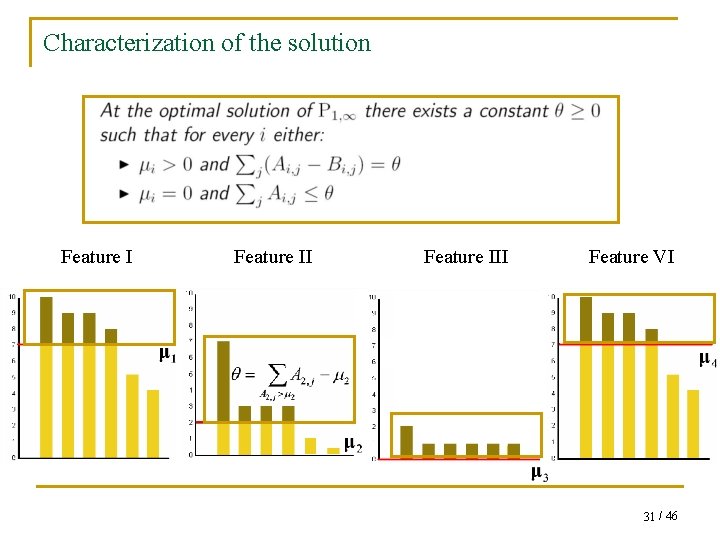
Characterization of the solution 1 30 / 46

Characterization of the solution Feature III Feature VI 31 / 46

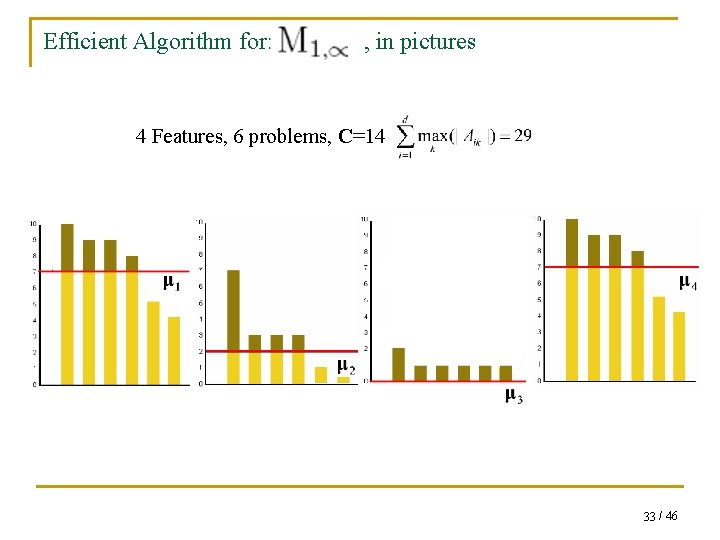
Mapping to a simpler problem q We can map the projection problem to the following problem which finds the optimal maximums μ: 32 / 46

Efficient Algorithm for: , in pictures 4 Features, 6 problems, C=14 33 / 46

Complexity q The total cost of the algorithm is dominated by a sort of the entries of A. q The total cost is in the order of: 34 / 46

Outline q An overview of transfer learning methods. q A joint sparse approximation model for transfer learning. q Asymmetric transfer experiments. q An efficient training algorithm. q Symmetric transfer image annotation experiments. 35 / 46

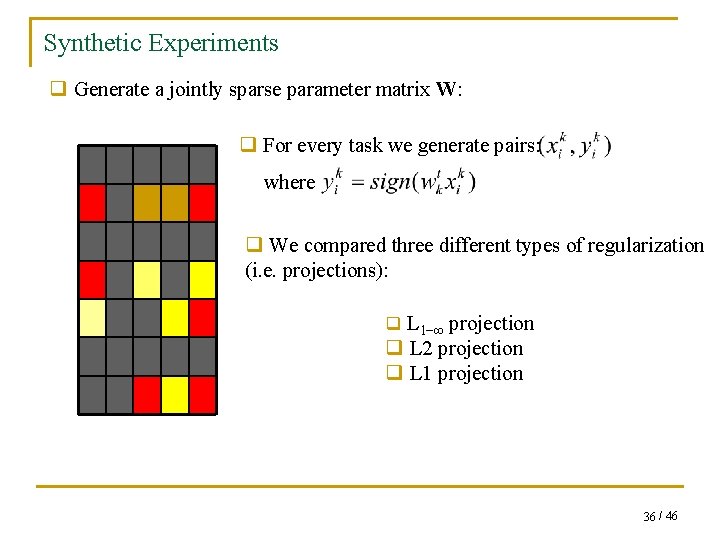
Synthetic Experiments q Generate a jointly sparse parameter matrix W: q For every task we generate pairs: where q We compared three different types of regularization (i. e. projections): q L 1−∞ projection q L 2 projection q L 1 projection 36 / 46

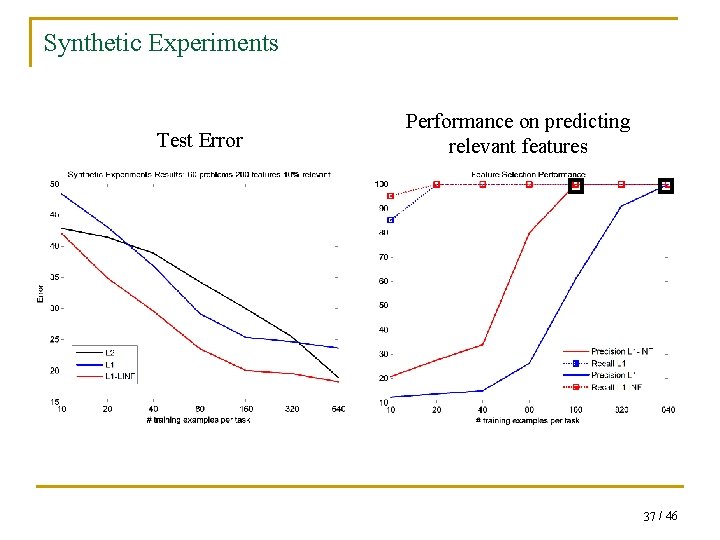
Synthetic Experiments Test Error Performance on predicting relevant features 37 / 46

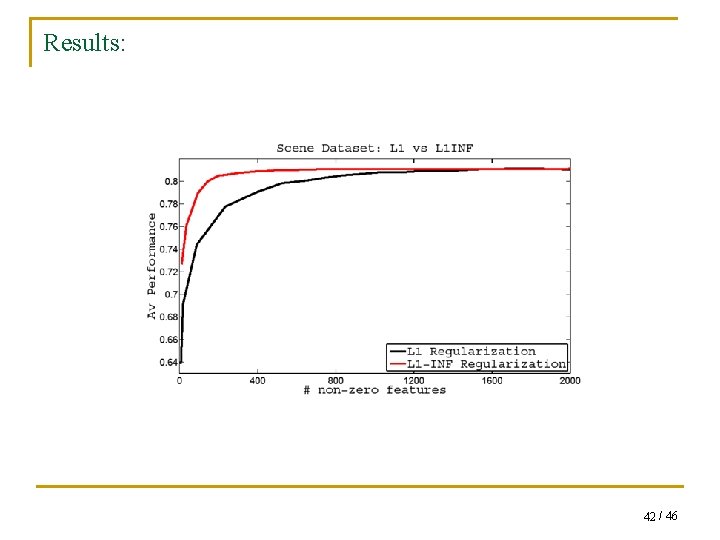
Dataset: Image Annotation president actress team q 40 top content words q Raw image representation: Vocabulary Tree (Grauman and Darrell 2005, Nister and Stewenius 2006) q 11000 dimensions 38 / 46

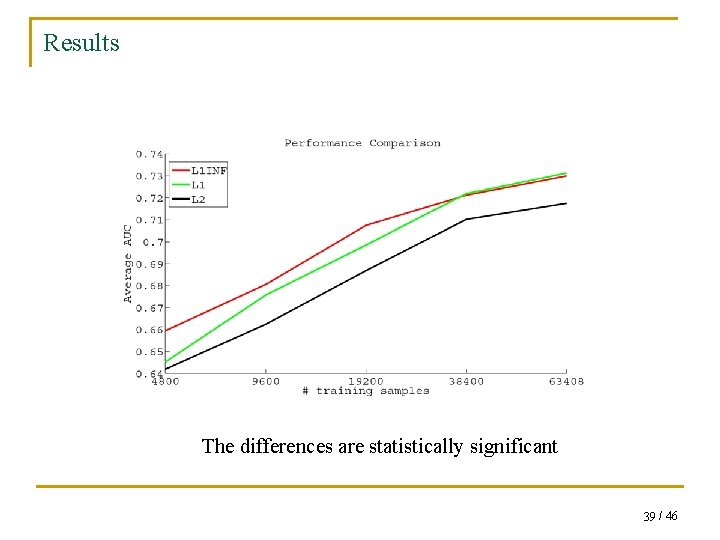
Results The differences are statistically significant 39 / 46

Results 40 / 46

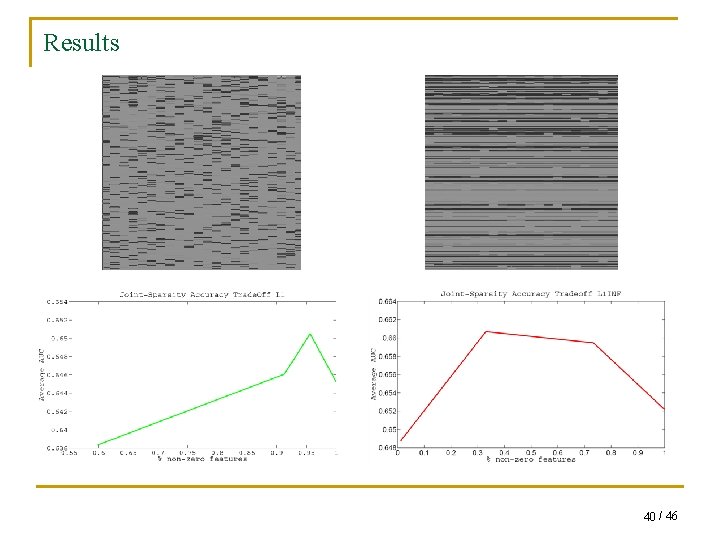
Dataset: Indoor Scene Recognition bakery bar Train station q 67 indoor scenes. q Raw image representation: similarities to a set of unlabeled images. q 2000 dimensions. 41 / 46

Results: 42 / 46

43

Summary of Thesis Contributions q A method that learns image representations using unlabeled images + meta-data. q A transfer model based on performing a joint loss minimization over the training sets of related tasks with a shared regularization. q Previous approaches used greedy coordinate descent methods. We propose an efficient global optimization algorithm for learning jointly sparse models. q A tool that makes implementing an L 1−∞ penalty as easy and almost as efficient as implementing the standard L 1 and L 2 penalties. q We presented experiments on real image classification tasks for both an asymmetric and symmetric transfer setting. 44 / 46

Future Work q Online Optimization. q Task Clustering. q Combining feature representations. q Generalization properties of L 1−∞ regularized models. 45 / 46

Thanks! 46 / 46