Transactions or Concurrency Control Definitions Schedule The order

Transactions or Concurrency Control

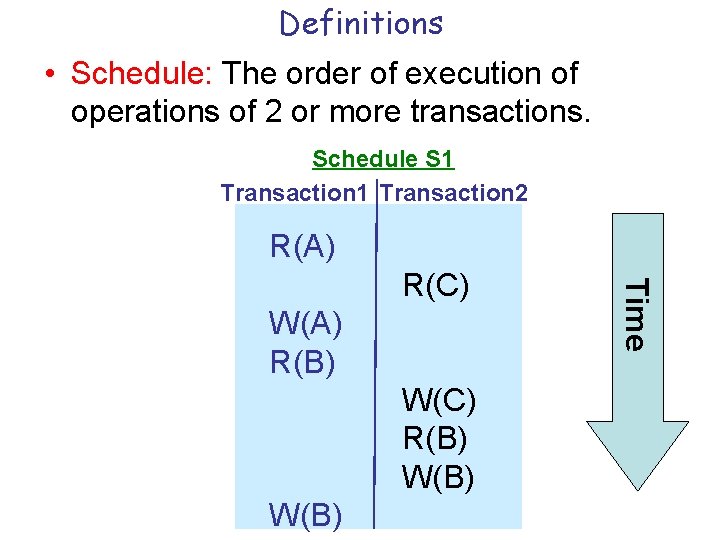
Definitions • Schedule: The order of execution of operations of 2 or more transactions. Schedule S 1 Transaction 2 R(A) W(A) R(B) W(C) R(B) W(B) Time R(C)

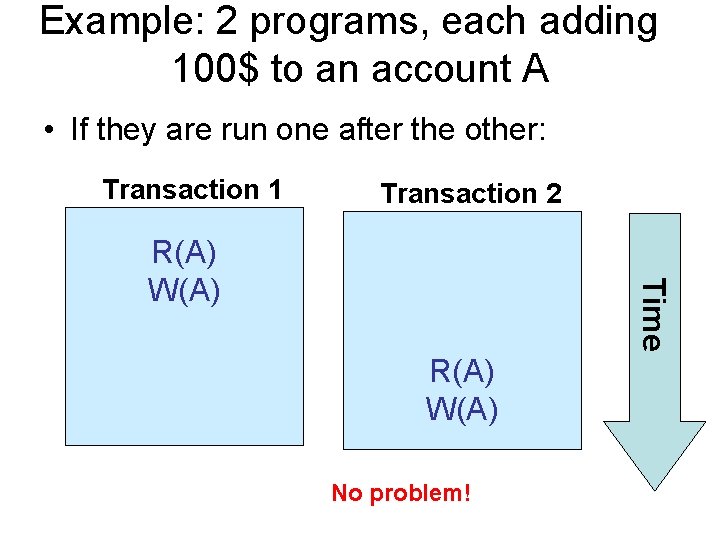
Example: 2 programs, each adding 100$ to an account A • If they are run one after the other: Transaction 1 Transaction 2 Time R(A) W(A) No problem!

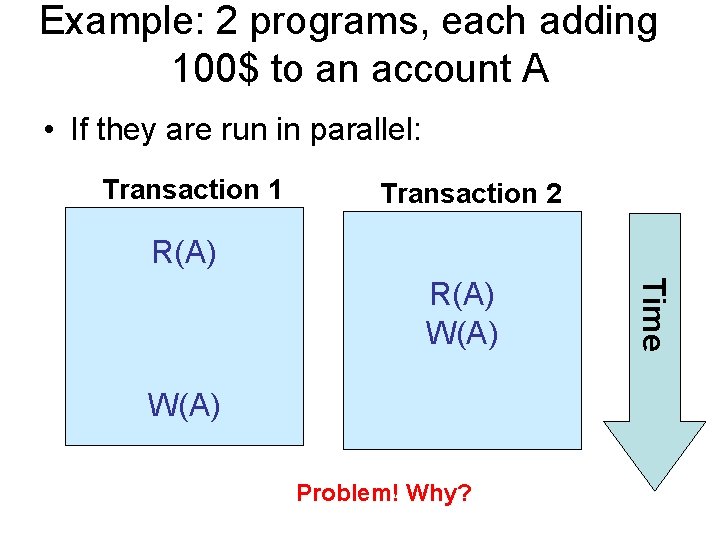
Example: 2 programs, each adding 100$ to an account A • If they are run in parallel: Transaction 1 Transaction 2 R(A) W(A) Problem! Why? Time R(A) W(A)

Definitions • Serial Schedule: A schedule in which the transactions are performed one after the other in a serial manner. Read(A) Write(A) Read(B) Write(B) Read(C) Write(C) Read(B) Write(B)

Schedules • A schedule is “correct” if it gives the same result as a serial schedule for any calculation. • Which of these “look” ok? Read(A) Write(A) Read(B) Write(B) Read(A) Write(A) Read(B) Write(B) Read(B) Write(B)

Schedules • Example for a “correct” schedule: Read(A) Write(A) Read(B) Write(B) Will always give the same result as Read(B) Write(B) Read(A) Write(A) Read(B) Write(B) And this will never cause an interleaving problem

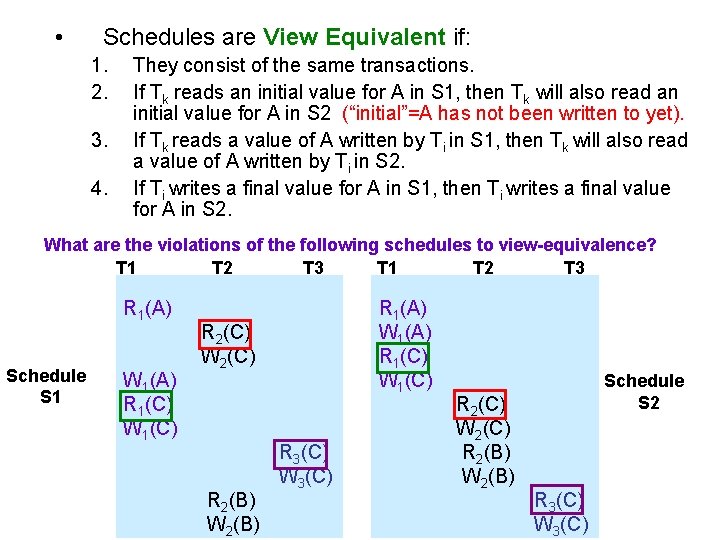
Schedules are View Equivalent if: 1. They consist of the same transactions. 2. If Tk reads an initial value for A in S 1, then Tk will also read an initial value for A in S 2 (“initial”=A has not been written to yet). 3. If Tk reads a value of A written by Ti in S 1, then Tk will also read a value of A written by Ti in S 2. 4. If Ti writes a final value for A in S 1, then Ti writes a final value for A in S 2.

• Schedules are View Equivalent if: 1. 2. 3. 4. They consist of the same transactions. If Tk reads an initial value for A in S 1, then Tk will also read an initial value for A in S 2 (“initial”=A has not been written to yet). If Tk reads a value of A written by Ti in S 1, then Tk will also read a value of A written by Ti in S 2. If Ti writes a final value for A in S 1, then Ti writes a final value for A in S 2. What are the violations of the following schedules to view-equivalence? T 1 T 2 T 3 R 1(A) Schedule S 1 W 1(A) R 1(C) W 1(C) R 1(A) W 1(A) R 1(C) W 1(C) R 2(C) W 2(C) R 2(B) W 2(B) R 3(C) W 3(C) R 2(C) W 2(C) R 2(B) W 2(B) Schedule S 2 R 3(C) W 3(C)

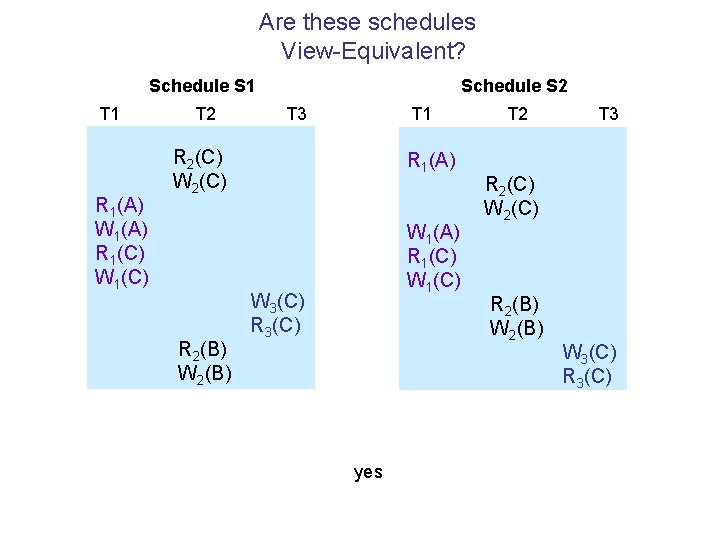
Are these schedules View-Equivalent? Schedule S 1 T 1 R 1(A) W 1(A) R 1(C) W 1(C) T 2 Schedule S 2 T 3 R 1(A) R 2(C) W 2(C) R 2(B) W 2(B) T 1 R 3(C) W 1(A) R 1(C) W 1(C) T 2 T 3 R 2(C) W 2(C) R 2(B) W 2(B) No, violation of first condition W 3(C) R 3(C)

Are these schedules View-Equivalent? Schedule S 1 T 1 R 1(A) W 1(A) R 1(C) W 1(C) T 2 Schedule S 2 T 3 T 1 R 2(C) W 2(C) R 2(B) W 2(B) R 1(A) W 1(A) R 1(C) W 3(C) R 3(C) yes T 2 T 3 R 2(C) W 2(C) R 2(B) W 3(C) R 3(C)

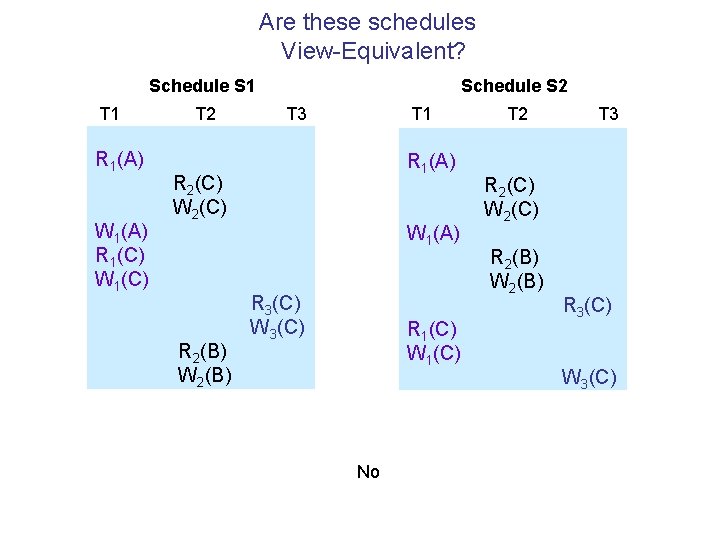
Are these schedules View-Equivalent? Schedule S 1 T 1 R 1(A) W 1(A) R 1(C) W 1(C) T 2 Schedule S 2 T 3 T 1 R 1(A) R 2(C) W 2(C) R 2(B) W 1(A) R 3(C) W 3(C) R 1(C) W 1(C) No T 2 T 3 R 2(C) W 2(C) R 2(B) W 2(B) R 3(C) W 3(C)

View-Equivalence • If 2 schedules are view-equivalent: – The same transactions will read the same values in both schedules – Therefore, they will also write the same values – This is true for any calculation

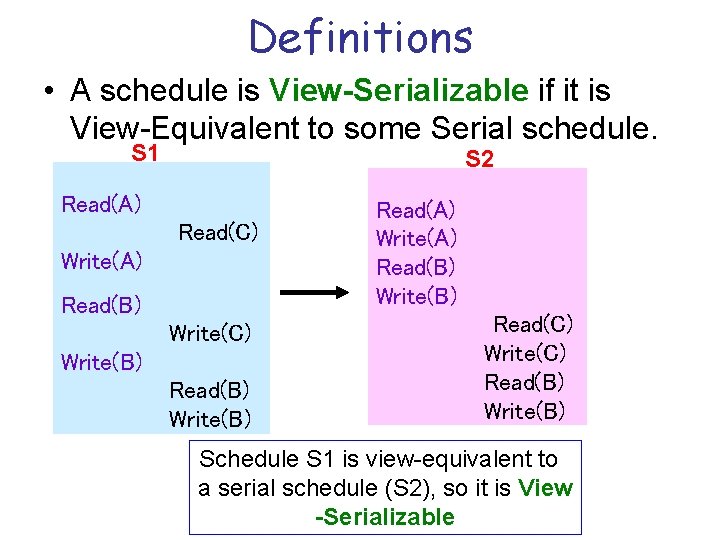
Definitions • A schedule is View-Serializable if it is View-Equivalent to some Serial schedule. S 1 S 2 Read(A) Read(C) Write(A) Read(B) Write(C) Write(B) Read(B) Write(B) Read(A) Write(A) Read(B) Write(B) Read(C) Write(C) Read(B) Write(B) Schedule S 1 is view-equivalent to a serial schedule (S 2), so it is View -Serializable

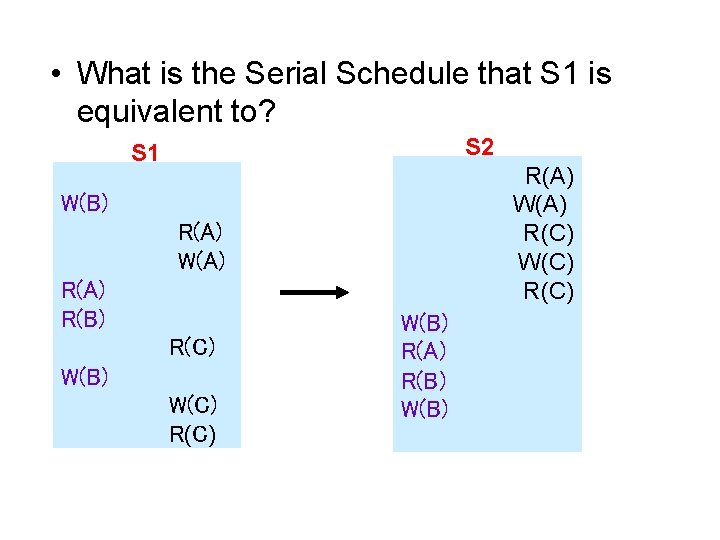
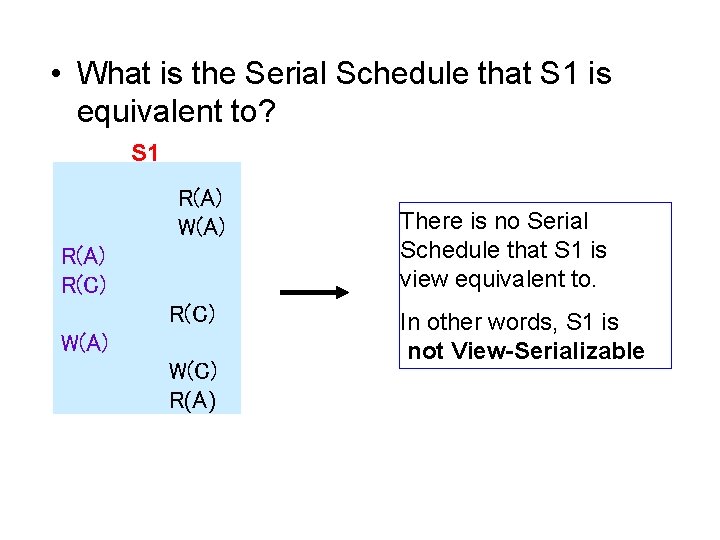
• What is the Serial Schedule that S 1 is equivalent to? S 2 S 1 R(A) W(A) R(C) W(C) R(C) W(B) R(A) W(A) R(B) R(C) W(B) W(C) R(C) W(B) R(A) R(B) W(B)

• What is the Serial Schedule that S 1 is equivalent to? S 1 R(A) W(A) R(C) W(A) W(C) R(A) There is no Serial Schedule that S 1 is view equivalent to. In other words, S 1 is not View-Serializable

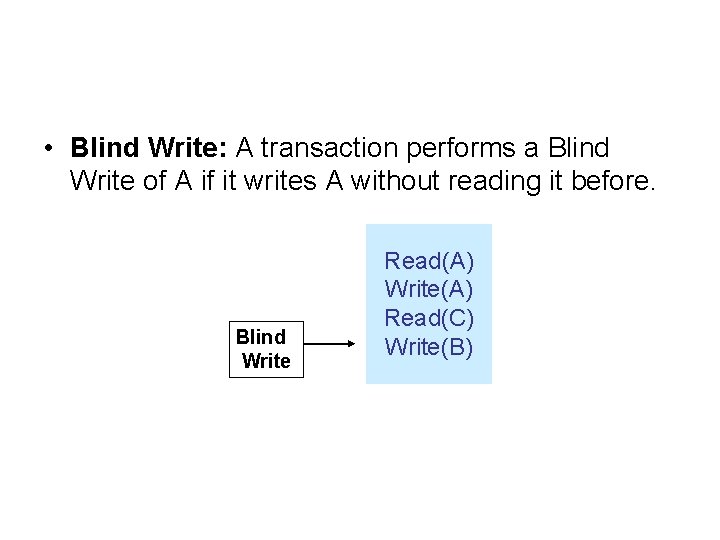
• Blind Write: A transaction performs a Blind Write of A if it writes A without reading it before. Blind Write Read(A) Write(A) Read(C) Write(B)

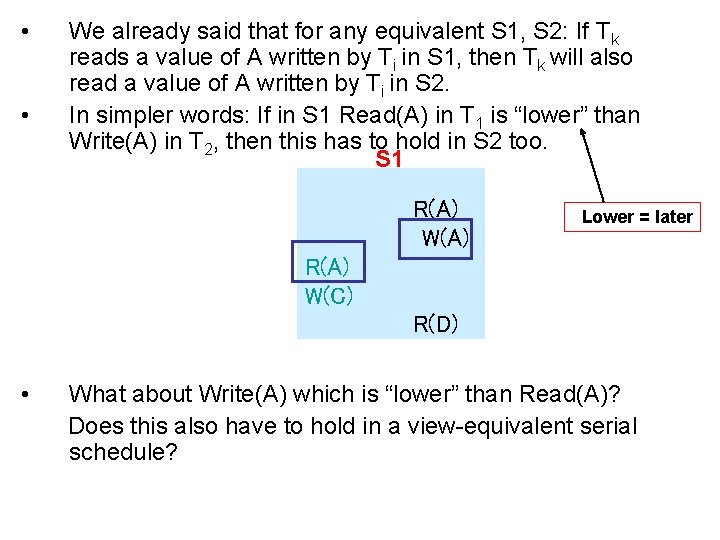
• • We already said that for any equivalent S 1, S 2: If Tk reads a value of A written by Ti in S 1, then Tk will also read a value of A written by Ti in S 2. In simpler words: If in S 1 Read(A) in T 1 is “lower” than Write(A) in T 2, then this has to hold in S 2 too. S 1 R(A) W(A) Lower = later R(A) W(C) R(D) • What about Write(A) which is “lower” than Read(A)? Does this also have to hold in a view-equivalent serial schedule?

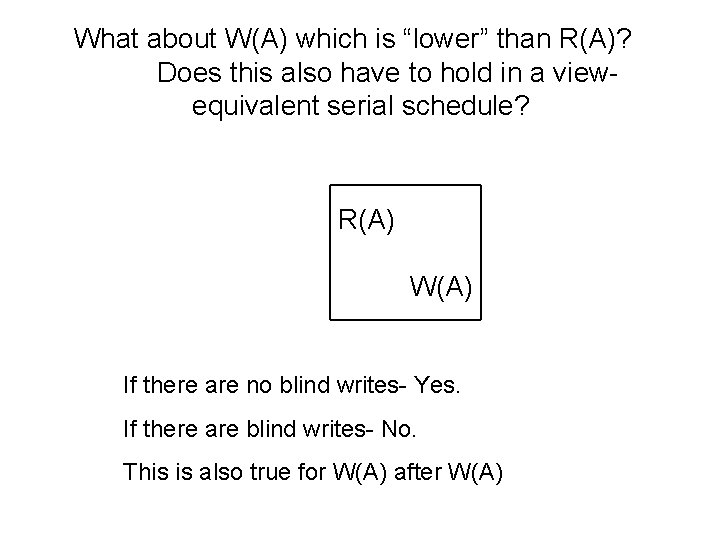
What about W(A) which is “lower” than R(A)? Does this also have to hold in a viewequivalent serial schedule? R(A) W(A) If there are no blind writes- Yes. If there are blind writes- No. This is also true for W(A) after W(A)

Formally: • Assuming there are no Blind Writes, and S 2 is an equivalent serial schedule : 1. If Tk writes a value of A which was previously read by Ti in S 1, then this will happen in S 2 too. 2. If Tk writes a value of A which was previously written by Ti in S 1, then this will happen in S 2 too.

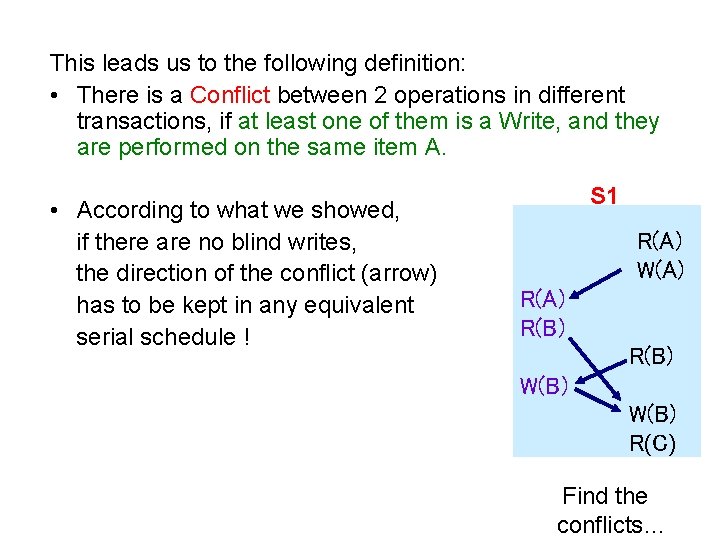
This leads us to the following definition: • There is a Conflict between 2 operations in different transactions, if at least one of them is a Write, and they are performed on the same item A. • According to what we showed, if there are no blind writes, the direction of the conflict (arrow) has to be kept in any equivalent serial schedule ! S 1 R(A) W(A) R(B) W(B) R(C) Find the conflicts…

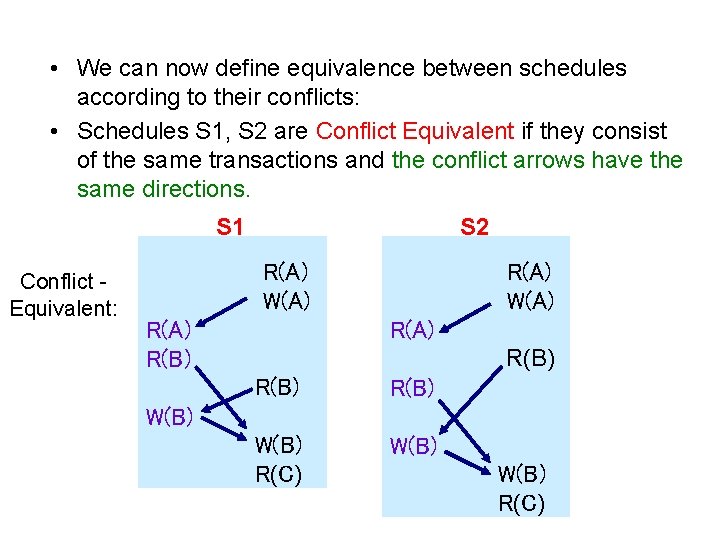
• We can now define equivalence between schedules according to their conflicts: • Schedules S 1, S 2 are Conflict Equivalent if they consist of the same transactions and the conflict arrows have the same directions. S 1 Conflict Equivalent: S 2 R(A) W(A) R(A) R(B) W(B) R(C) W(B) R(C)

• Lemma: Conflict Equivalence => View Equivalence (this is true even if there are Blind Writes!) Schedules are Conflict Equivalent if: 1. 2. They consist of the same transactions. The conflict arrows have the same directions. Schedules are View Equivalent if: 1. 2. 3. 4. They consist of the same transactions. If Tk reads an initial value for A in S 1, then Tk will also read an initial value for A in S 2 If Tk reads a value of A written by Ti in S 1, then Tk will also read a value of A written by Ti in S 2. If Ti writes a final value for A in S 1, then Ti writes a final value for A in S 2. Proof: We assume S 1 and S 2 are Conflict Equivalent. We need to prove 1 -4 from above.

• Schedule S 1 is Conflict Serializable if it is Conflict. Equivalent to some serial schedule S 2. • Conflict Serializable => View Serializable (directly from the Lemma). • The other direction is not necessarily true if there are Blind Writes: T 1 T 2 T 3 There is no serial R(A) schedule which is W(A) S 1 conflict. W(A) equivalent to s 1 W(A) S 2 T 1 R(A) W(A) T 2 T 3 W(A) But S 2 is serial and is viewequivalent to S 1

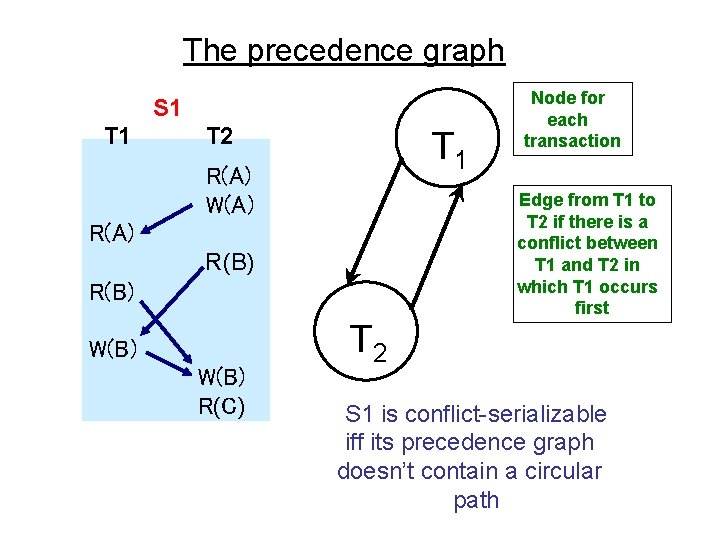
The precedence graph S 1 T 2 T 1 R(A) W(A) R(B) W(B) R(C) T 2 Node for each transaction Edge from T 1 to T 2 if there is a conflict between T 1 and T 2 in which T 1 occurs first S 1 is conflict-serializable iff its precedence graph doesn’t contain a circular path

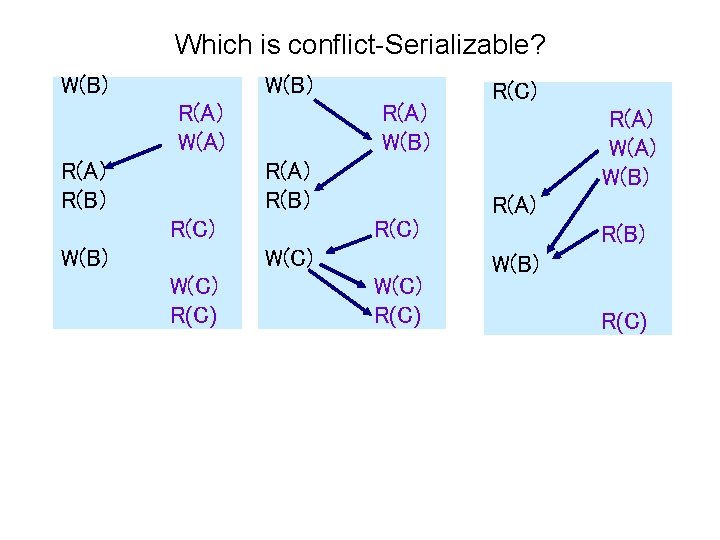
Which is conflict-Serializable? W(B) R(A) W(A) R(B) R(A) W(B) R(A) R(B) R(C) W(C) R(C) R(A) W(B) R(A) R(B) W(B) R(C)