Traffic Flow in Networks Scaling Conjectures Physical Evidence

Traffic Flow in Networks: Scaling Conjectures, Physical Evidence, and Control Applications Carlos F. Daganzo U. C. Berkeley Center for Future Urban Transport www. its. berkeley. edu/volvocenter/ Luminy, October 2007

References 1. Daganzo, C. F. (1996) “The nature of freeway gridlock and how to prevent it" in Transportation and Traffic Theory, Proc. 13 th Int. Symp. Trans. Traffic Theory (J. B. Lesort, ed) pp. 629 646, Pergamon Elsevier, Tarrytown, N. Y. 2. Daganzo, C. F. (2007) “Urban gridlock: macroscopic modeling and mitigation approaches” Transportation Research B 41, 49 -62; “corrigendum” Transportation Research B 41, 379. 3. Daganzo, C. F. and Geroliminis, N. (2007) “How to predict the macroscopic fundamental diagram of urban traffic” Working paper, Volvo Center of Excellence on Future Urban Transport, Univ. of California, Berkeley, CA (submitted). 4. Geroliminis N. , Daganzo C. F. (2007 a) “Macroscopic modeling of traffic in cities” 86 th Annual Meeting Transportation Research Board, Washington D. C. 5. Geroliminis, N. and Daganzo, C. F. (2007 b) “Existence of urban-scale macroscopic fundamental diagrams: some experimental findings” Working paper, Volvo Center of Excellence on Future Urban Transport, Univ. of California, Berkeley, CA (submitted). 2

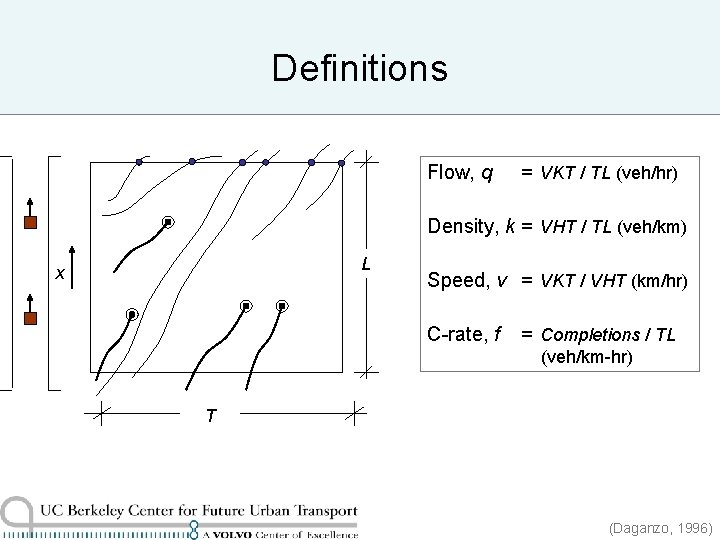
Definitions Flow, q = VKT / TL (veh/hr) Density, k = VHT / TL (veh/km) L x Speed, v = VKT / VHT (km/hr) C-rate, f = Completions / TL (veh/km-hr) T (Daganzo, 1996)

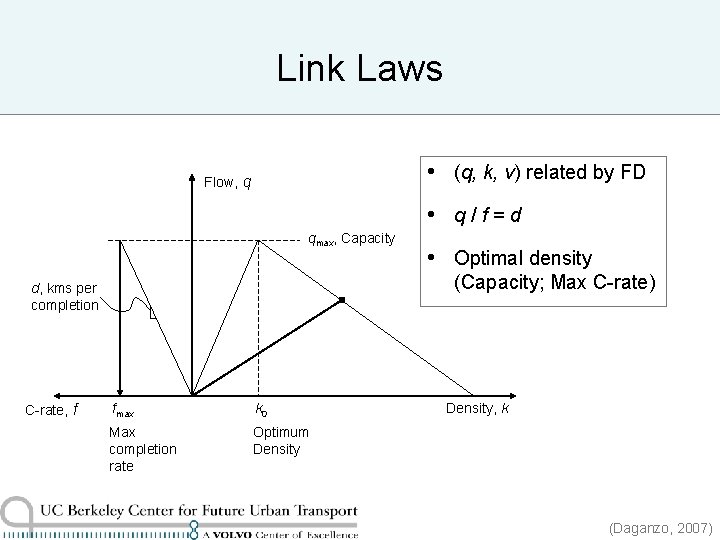
Link Laws • (q, k, v) related by FD Flow, q • q/f=d qmax, Capacity (Capacity; Max C-rate) d, kms per completion C-rate, f • Optimal density fmax k 0 Max completion rate Optimum Density, k (Daganzo, 2007)

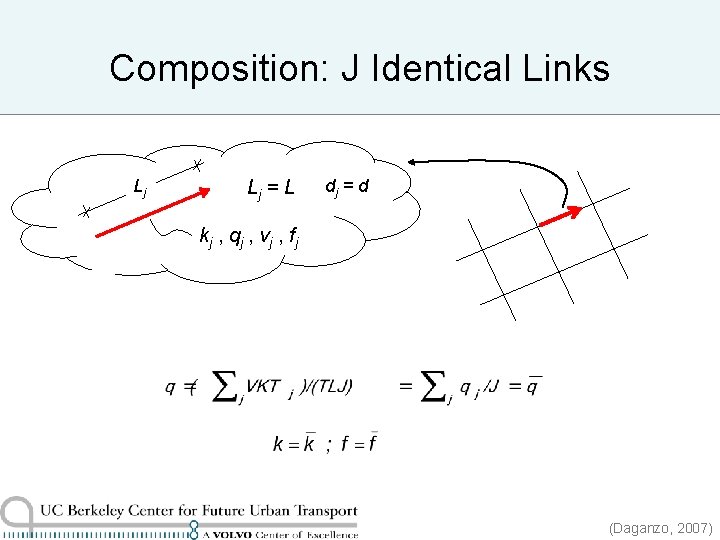
Composition: J Identical Links Lj Lj = L dj = d kj , qj , vj , fj (Daganzo, 2007)

Conjectures Network of identical links: Flow Real Networks: Jensen’s inequality: q ≤ Q(k) ( ki , qi ) q q ~ Q(k) • An MFD exists • If vi ~ constant: / ( ki , qi )Network Tripd completions f ~ Q(k) / d flow ~ Constant f C-rate Density (Daganzo, 2007)

Outflow San Francisco Simulation: No Control Vehicle Accumulation (Geroliminis & Daganzo, 2007 a)

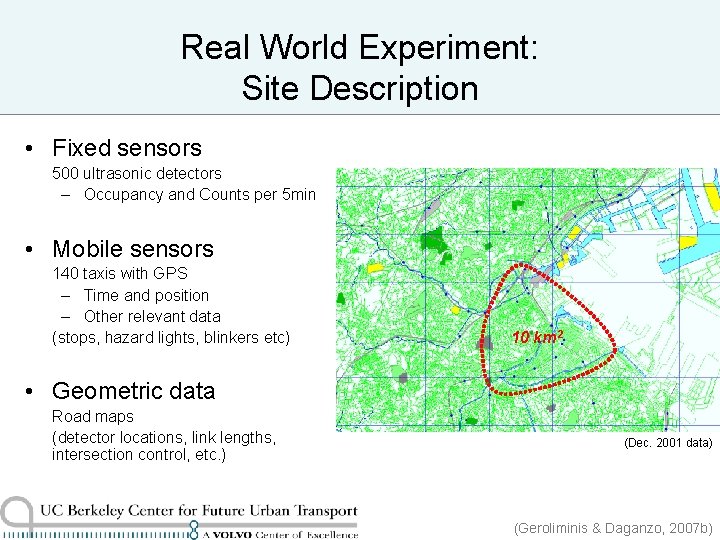
Real World Experiment: Site Description • Fixed sensors 500 ultrasonic detectors – Occupancy and Counts per 5 min • Mobile sensors 140 taxis with GPS – Time and position – Other relevant data (stops, hazard lights, blinkers etc) 10 km 2 • Geometric data Road maps (detector locations, link lengths, intersection control, etc. ) (Dec. 2001 data) (Geroliminis & Daganzo, 2007 b)

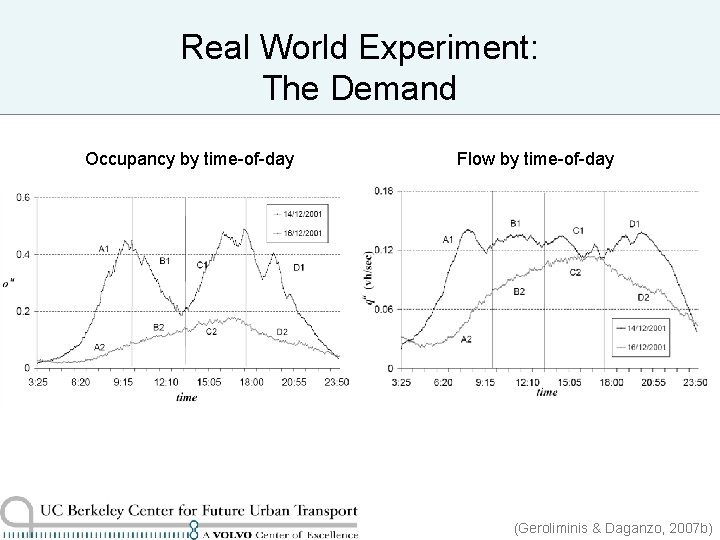
Real World Experiment: The Demand Occupancy by time-of-day Flow by time-of-day (Geroliminis & Daganzo, 2007 b)

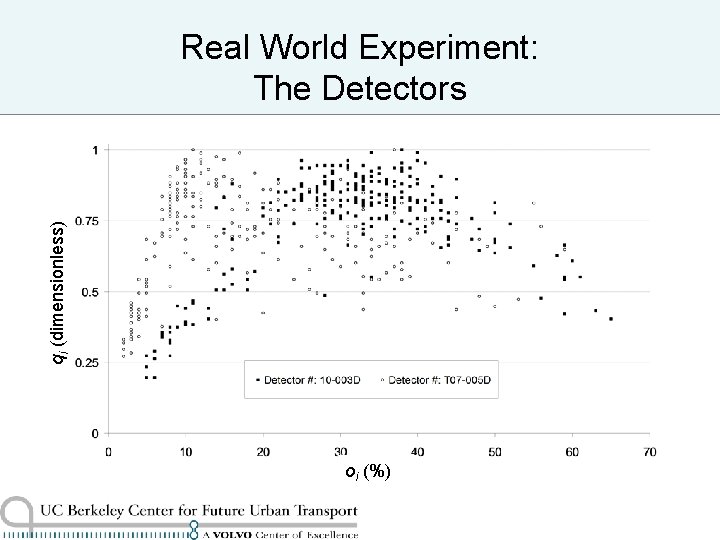
qi (dimensionless) Real World Experiment: The Detectors oi (%)

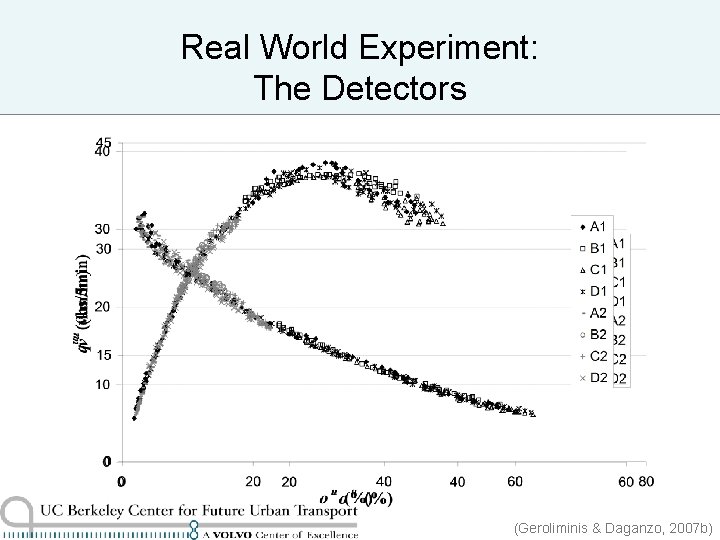
Real World Experiment: The Detectors (Geroliminis & Daganzo, 2007 b)

Real World Experiment: Taxis Conjecture: Passenger carrying taxis use the same parts of the network as cars Then: (Geroliminis & Daganzo, 2007 b)

Filters to determine full vs. empty taxis A stop is a passenger move, if: • • hazard lights are ON or parking brake is used or left blinker is ON and taxi stops > 45 sec or speed < 3 km/hr for >60 sec A trip is valid if: • trip duration > 5 min and length > 1. 5 km • trip distance < 2 × “Euclidean distance” and (Geroliminis & Daganzo, 2007 b)

Illustration of Filter Results (Geroliminis & Daganzo, 2007 b)

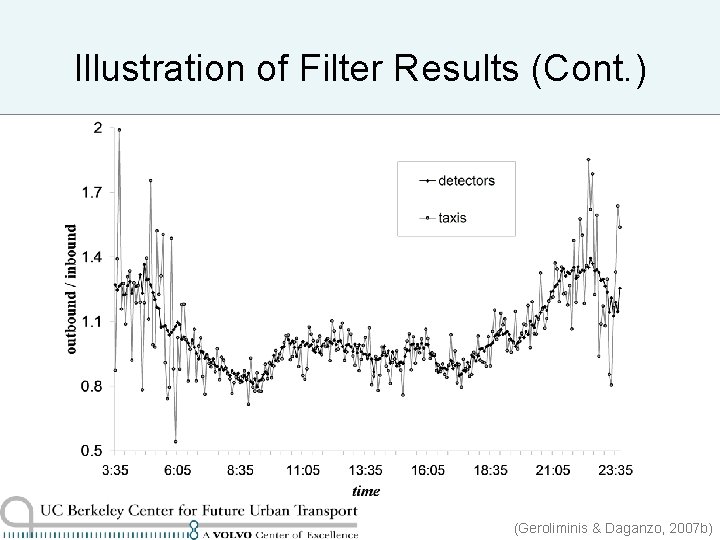
Illustration of Filter Results (Cont. ) (Geroliminis & Daganzo, 2007 b)

Real World Experiment: Taxis Conjecture: Passenger carrying taxis use the same parts of the network as cars Then: (Geroliminis & Daganzo, 2007 b)

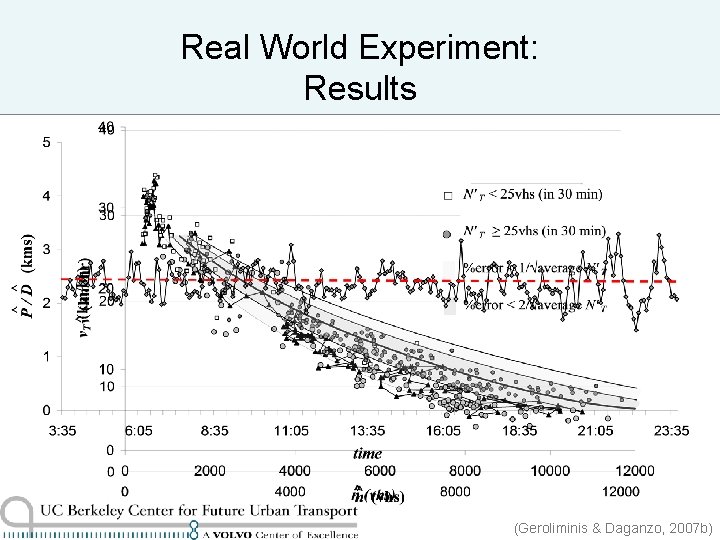
Real World Experiment: Results (Geroliminis & Daganzo, 2007 b)

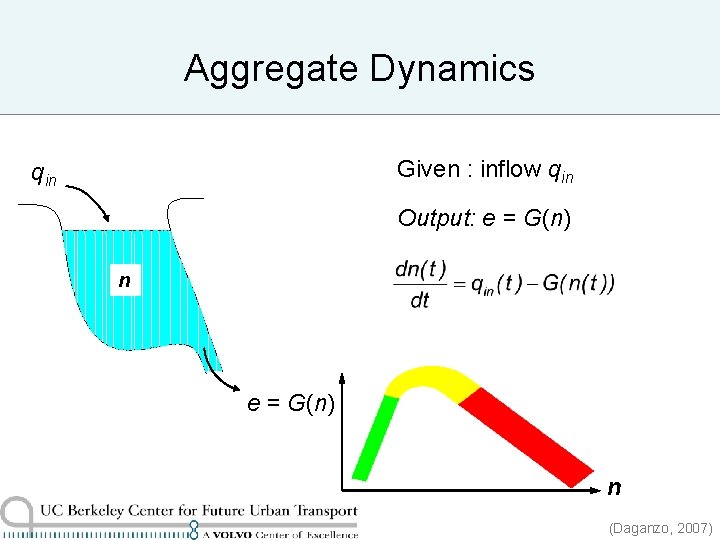
Aggregate Dynamics Given : inflow qin Output: e = G(n) n (Daganzo, 2007)

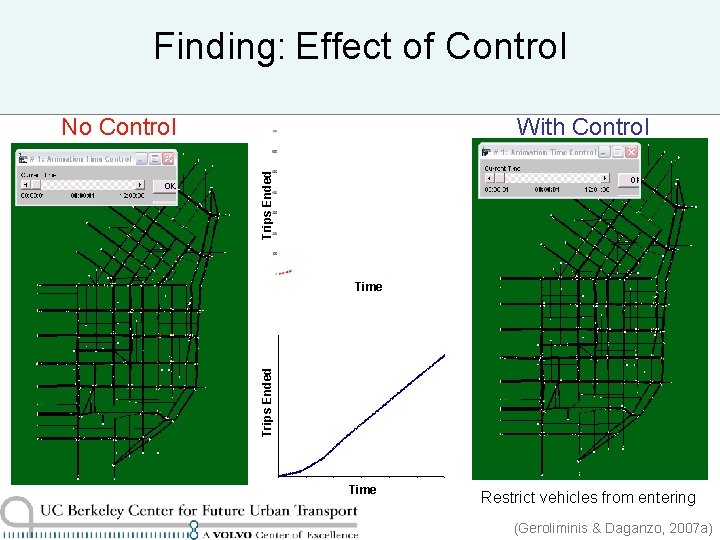
Finding: Effect of Control No Control Trips Ended With Control Trips Ended Time Restrict vehicles from entering (Geroliminis & Daganzo, 2007 a)

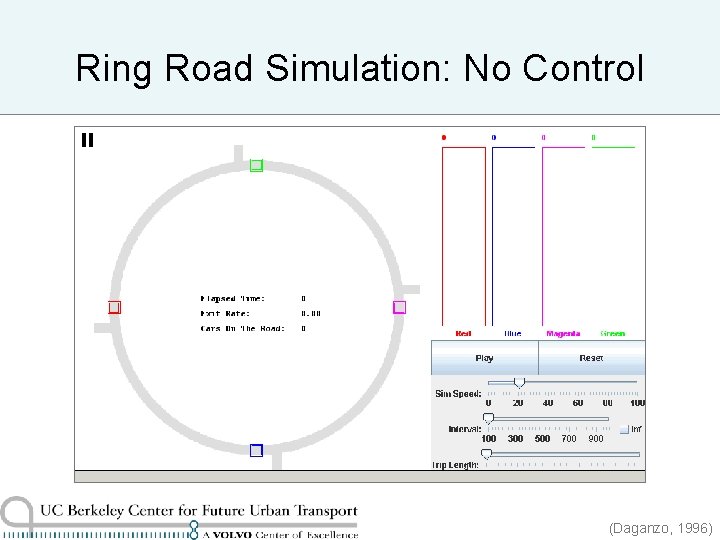
Ring Road Simulation: No Control (Daganzo, 1996)

Ring Road Simulation: Control (Daganzo, 1996)

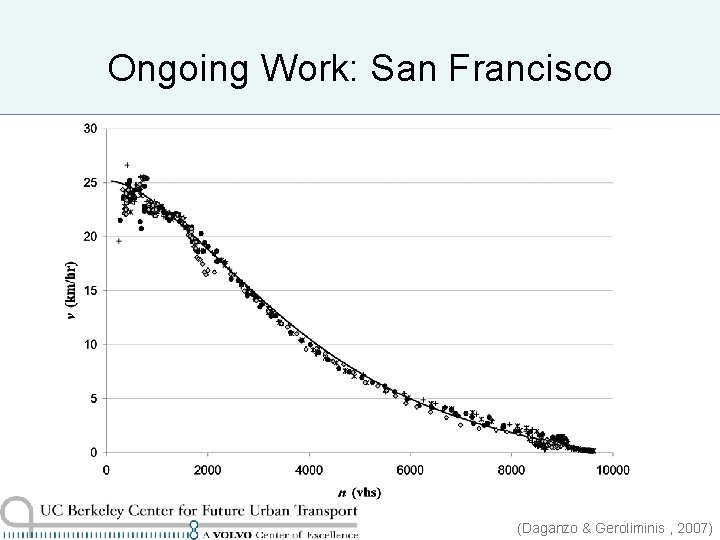
Ongoing Work: San Francisco (Daganzo & Geroliminis , 2007)