Traditional Keynesian Theories of Fluctuations From Romer chapter

Traditional Keynesian Theories of Fluctuations (From Romer, chapter 6 part A, section 7. 8) • • Microfundations The IS-LM-AD model The liquidity trap and the post 2008 crisis The supply curve The open economy and exchange rate overshooting The Phillips curve The natural rate of unemployment The Canonical New-Keynesian model • Introduction

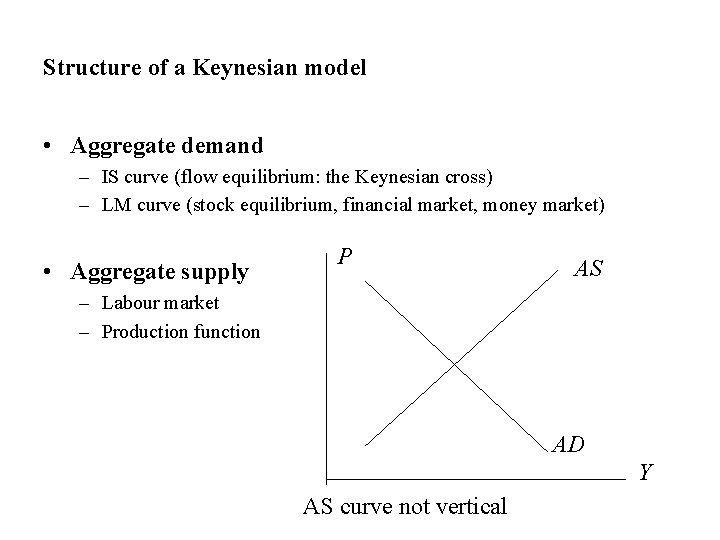
Structure of a Keynesian model • Aggregate demand – IS curve (flow equilibrium: the Keynesian cross) – LM curve (stock equilibrium, financial market, money market) • Aggregate supply P AS – Labour market – Production function AD Y AS curve not vertical

IS-LM model with fixed prices • Nominal rigidities are given (fixed prices) • Time is discrete capital is fixed, closed economy, no government to start with • The production function is:

Household optimization problem • Fixed number of infinitely lived households • They get utility from consumption, holding money, and disutility from working • We ignore population growth and normalize the number of household to 1

Household objective function is

Utility functions (C and M) are CRRA The assumption that Money enter the utility function is a short cut Observationally equivalent to transaction purpose (Fenstra 1986)

Money and Bonds: Two assets • The two assets are substitute • Bonds bears interest rate but are not liquid (i. e. , in the U function)

• For households, paths of P, W, and I are given • Path of C and M are chosen in order to maximize 6. 2 subject to (6. 5) and the No-Ponzi game condition • For the moment, L is exogenous • Path of M is set by the central bank

New Keynesian IS curve • Following Romer intuitive methodology to derive the Euler equation (last paragraph of page 240) with the real interest rate is:

• • Y(t+1) is added to the traditional IS curve With uncertainty, we have instead E(Y(t+1) Inverse relationship between Y(t) and r(t). Relationship is strengthen with the introduction of capital and investment (chapter 9 of book)

LM curve • Again following Romer approach to optimization (bottom of page 241 do it yourself). • First order condition for money holding (an increase in m increase utility of money holding but decrease return on bond holding and consumption (6. 9)

• The LM curve in increasing in output and decreasing in the nominal interest rate (explanation) • Interest rate rule is the modern approach to close the system

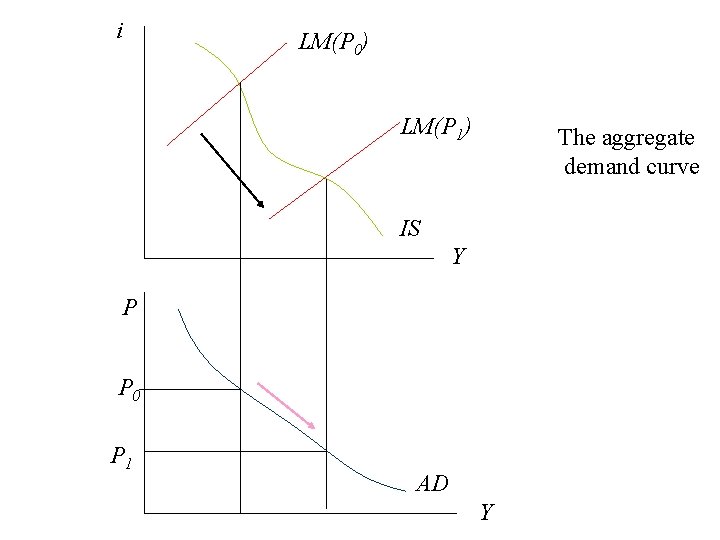
i LM(P 0) LM(P 1) The aggregate demand curve IS Y P P 0 P 1 AD Y

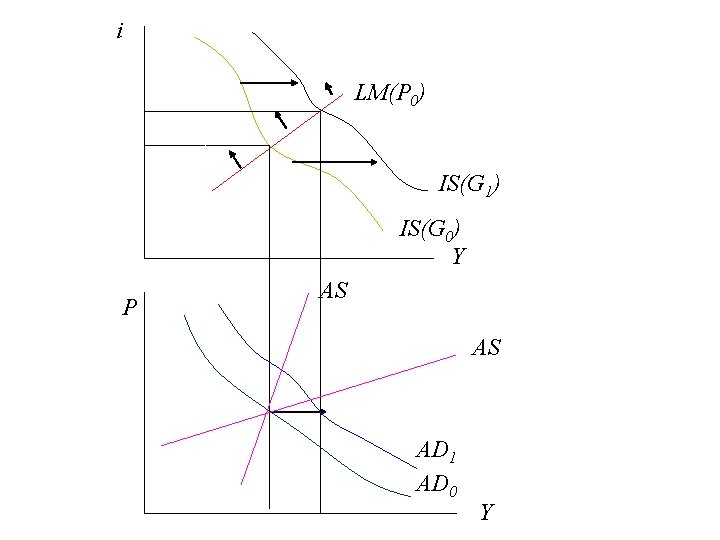
i LM(P 0) IS(G 1) IS(G 0) Y P AS AS AD 1 AD 0 Y

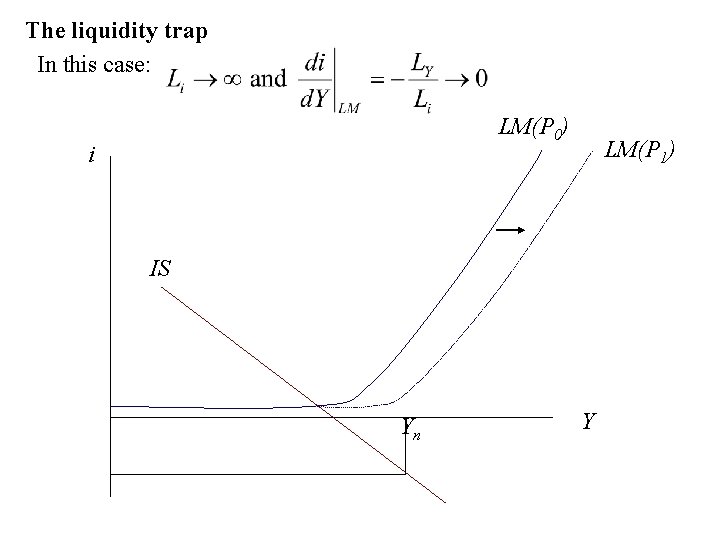
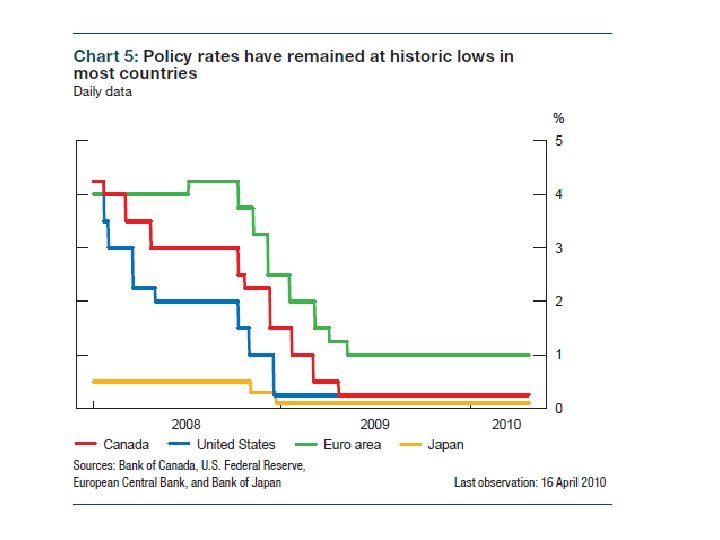
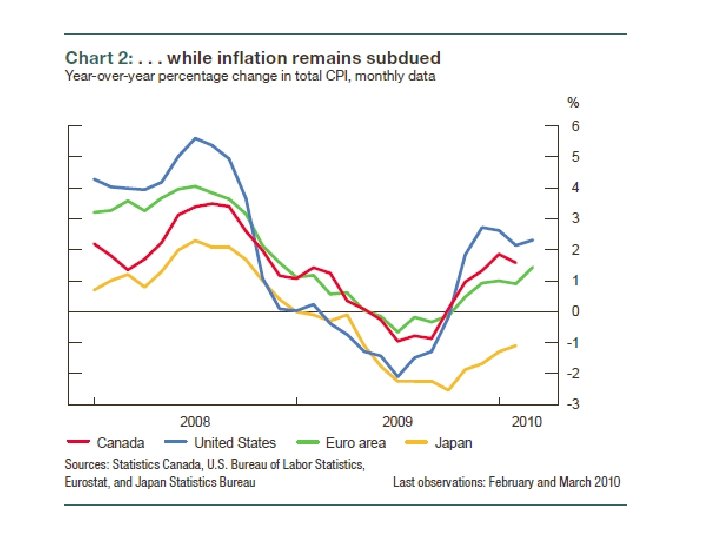
The liquidity trap In this case: LM(P 0) i LM(P 1) IS Yn Y

-What is the shape of the AD curve in this case? -What happen if the AS curve is vertical (classical) -What about the Pigou effect? -This is related to Summers (1991)

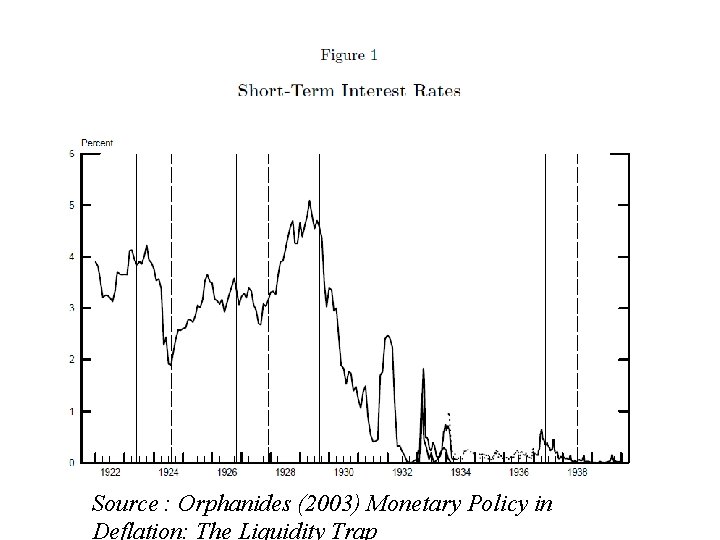
Source : Orphanides (2003) Monetary Policy in Deflation: The Liquidity Trap

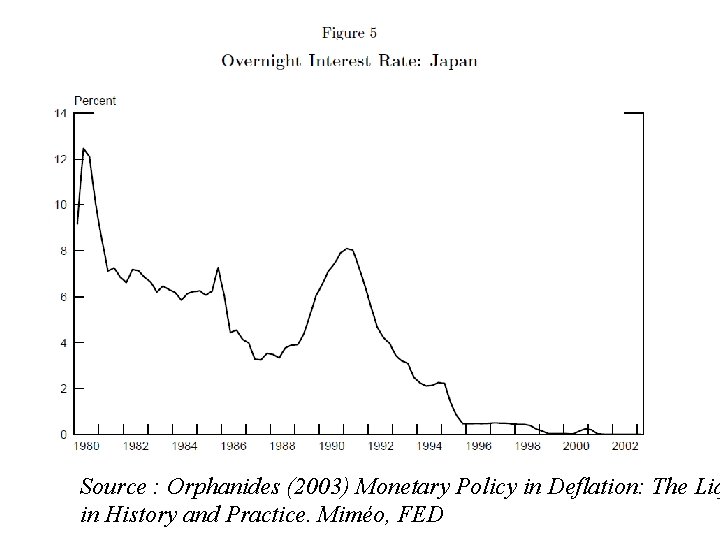
Source : Orphanides (2003) Monetary Policy in Deflation: The Liq in History and Practice. Miméo, FED

• • • The remedy should come, I suggest, from a general recognition that the rate of investment need not be beyond our control, if we are prepared to use our banking systems to effect a proper adjustment of the market-rate of interest. It might be sufficient merely to produce a general belief in the long continuance of a very low rate of short-term interest. The change, once it has begun, will feed on itself. . The Bank of England the Federal Reserve Board. . . should pursue bank -rate policy and open-market operations a outrance. . . [t]hat is to say, they should combine to maintain a very low level of the short-term rate of interest, and buy long-dated securities. . . until the short-term market is saturated.

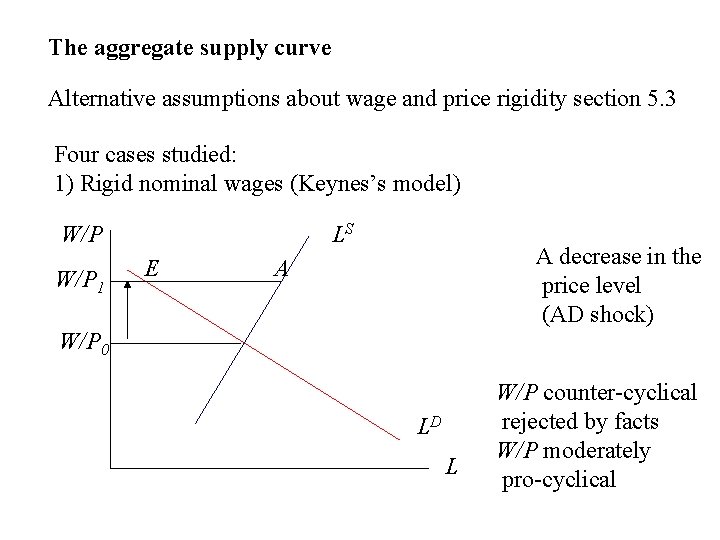
The aggregate supply curve Alternative assumptions about wage and price rigidity section 5. 3 Four cases studied: 1) Rigid nominal wages (Keynes’s model) W/P 1 LS E A decrease in the price level (AD shock) A W/P 0 LD L W/P counter-cyclical rejected by facts W/P moderately pro-cyclical

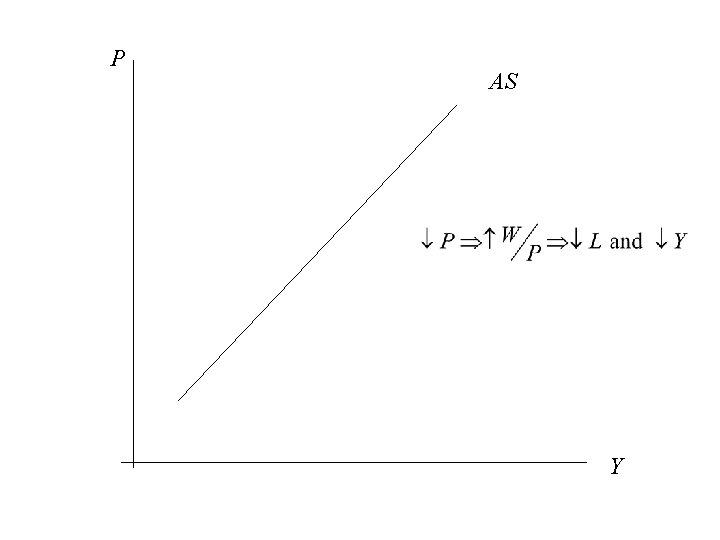
P AS Y

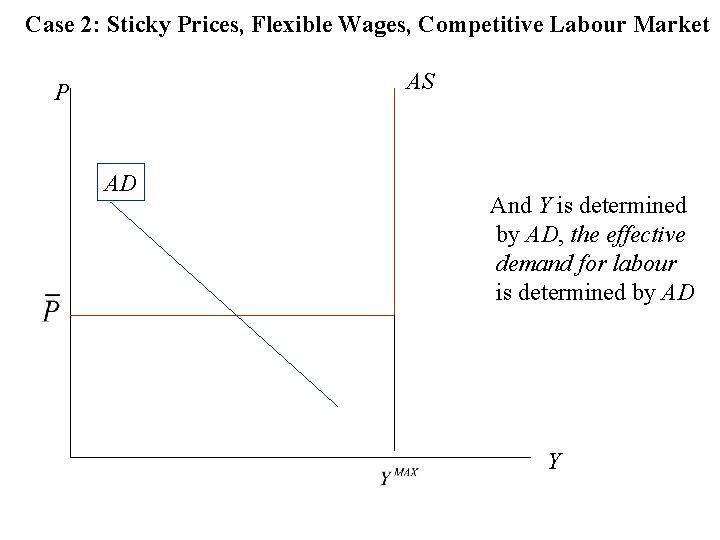
Case 2: Sticky Prices, Flexible Wages, Competitive Labour Market AS P AD And Y is determined by AD, the effective demand for labour is determined by AD Y

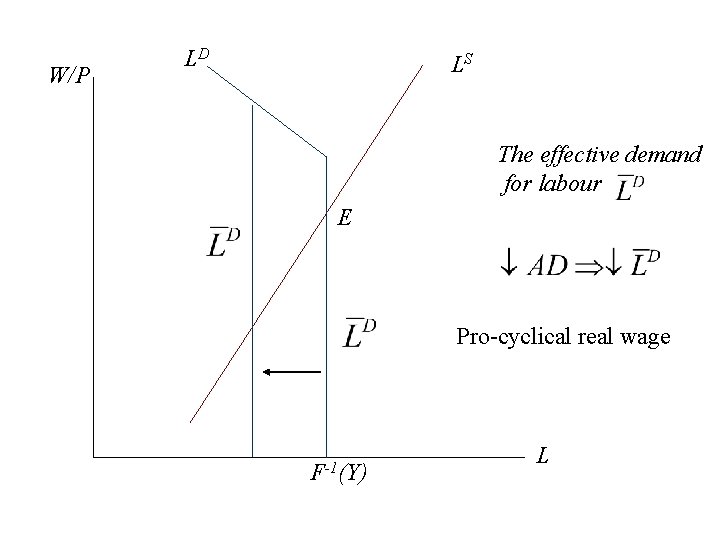
W/P LD LS The effective demand for labour E Pro-cyclical real wage F-1(Y) L

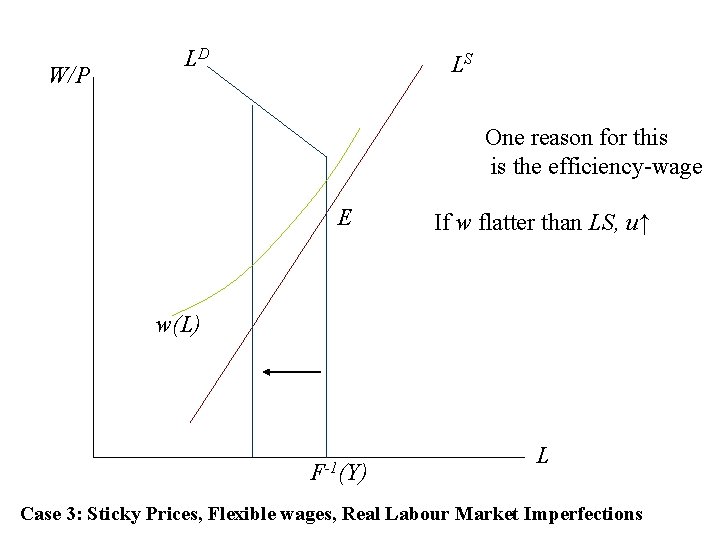
W/P LD LS One reason for this is the efficiency-wage E If w flatter than LS, u↑ w(L) F-1(Y) L Case 3: Sticky Prices, Flexible wages, Real Labour Market Imperfections

Case 4: Sticky Wages, Flexible Prices, Imperfect Competition Markup function If μ is fixed, W/P counter cyclical as in case 1 However, if μ is countercyclical (strong evidences), the real wage can be acyclical or procyclical.