Towards Robust Indexing for Ranked Queries Dong Xin

Towards Robust Indexing for Ranked Queries Dong Xin, Chen, Jiawei Han Department of Computer Science University of Illinois at Urbana-Champaign VLDB 2006

Outline • Introduction • Robust Index • Compute Robust Index – Exact Solution – Approximate Solution – Multiple Indices • Performance Study • Discussion and Conclusions 2

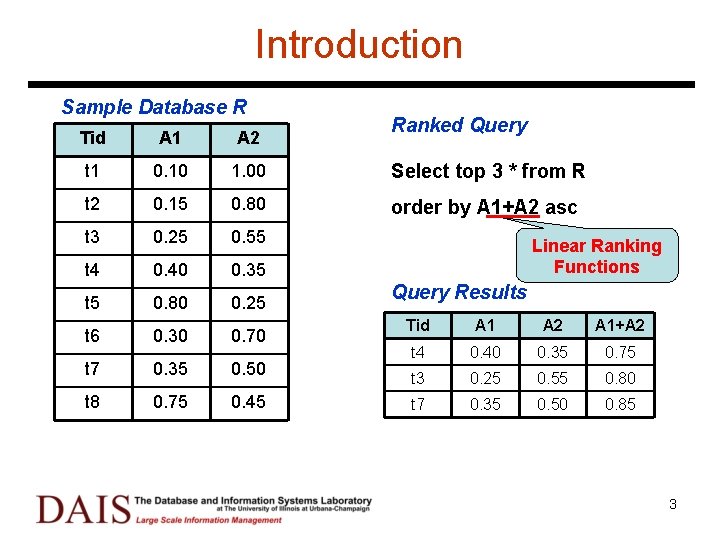
Introduction Sample Database R Ranked Query Tid A 1 A 2 t 1 0. 10 1. 00 Select top 3 * from R t 2 0. 15 0. 80 order by A 1+A 2 asc t 3 0. 25 0. 55 t 4 0. 40 0. 35 t 5 0. 80 0. 25 t 6 0. 30 0. 70 t 7 0. 35 0. 50 t 8 0. 75 0. 45 Linear Ranking Functions Query Results Tid A 1 A 2 A 1+A 2 t 4 0. 40 0. 35 0. 75 t 3 0. 25 0. 55 0. 80 t 7 0. 35 0. 50 0. 85 3

Efficient Processing of Ranked Queries • Naïve Solution: scan the whole database and evaluate all tuples • Using indices or materialized views – Distributed Indexing • Sort each attribute individually and merge attributes by a threshold algorithm (TA) [Fagin et al, PODS’ 96, ’ 99, ’ 01] – Spatial Indexing • Organize tuples into R-tree and determine a threshold to prune the search space [Goldstain et al, PODS’ 97] • Organize tuples into R-tree and retrieve data progressively [Papadias et al, SIGMOD’ 03] – Sequential Indexing • Organize tuples into convex hulls [Chang et al, SIGMOD’ 00] • Materialize ranked views according to the preference functions [Hristidis et al, SIGMOD’ 01] – And More… 4

Sequential Indexing • Sequential Index (ranked view) – Linearly sort tuples – No sophisticated data structures – Sequential data access (good for database I/O) • Representative work – Onion [Chang et al, SIGMOD’ 00] – PREFER [Hristidis et al, SIGMOD’ 01] • Our proposal: Robust Index 5

Review: Onion Technique Sample Database R Tid A 1 A 2 t 1 0. 10 1. 00 t 2 0. 15 0. 80 t 3 0. 25 0. 55 t 4 0. 40 0. 35 t 5 0. 80 0. 25 t 6 0. 30 0. 70 t 7 0. 35 0. 50 t 8 0. 75 0. 45 Ranked Query Select top 3 * from R A 1 Index by Convex hull t 1 t 2 t 6 t 3 t 7 Second layer Retrieve data layer by layer until the top-k results are found t 8 t 4 In worst case, retrieve top-k layers of tuples t 5 A 1 First layer A 2 t 1 t 2 t 6 t 3 t 7 order by a. A 1+b. A 2 asc Second layer t 8 Index by Convex Shell t 4 First layer If a and b are non-negative (a, b are weighing parameters in linear ranking function) Expect less number of tuples in each layer t 5 A 2 6

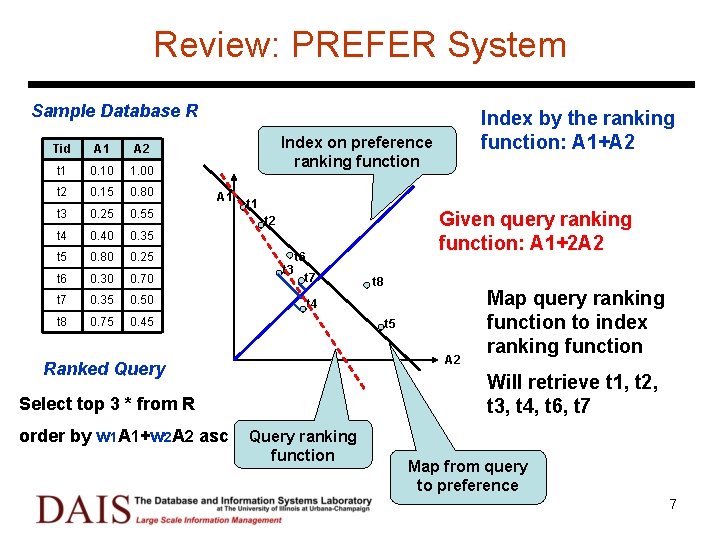
Review: PREFER System Sample Database R Tid A 1 A 2 t 1 0. 10 1. 00 t 2 0. 15 0. 80 t 3 0. 25 0. 55 t 4 0. 40 0. 35 t 5 0. 80 0. 25 t 6 0. 30 0. 70 t 7 0. 35 0. 50 t 8 0. 75 0. 45 Index by the ranking function: A 1+A 2 Index on preference ranking function A 1 t 1 Given query ranking function: A 1+2 A 2 t 6 t 3 t 7 t 4 t 5 A 2 Ranked Query Map query ranking function to index ranking function Will retrieve t 1, t 2, t 3, t 4, t 6, t 7 Select top 3 * from R order by w 1 A 1+w 2 A 2 asc t 8 Query ranking function Map from query to preference 7

Comments on Sequential Indexing • PREFER – Works extremely well when query functions are close to the index function; Sensitive to query weights • Onion – Less sensitive to query weights; Can we do better? • Both methods – Require considerable online computation • Motivation for robust indexing – Not sensitive to query weights – Push most computation to index building phase Average #tuples retrieved for 10 random queries asking for top 50 answers Query weights are randomly selected from 1, 2, 3, 4 8

Outline • Introduction • Robust Index • Compute Robust Index – Exact Solution – Approximate Solution – Multiple Indices • Performance Study • Discussion and Conclusions 9

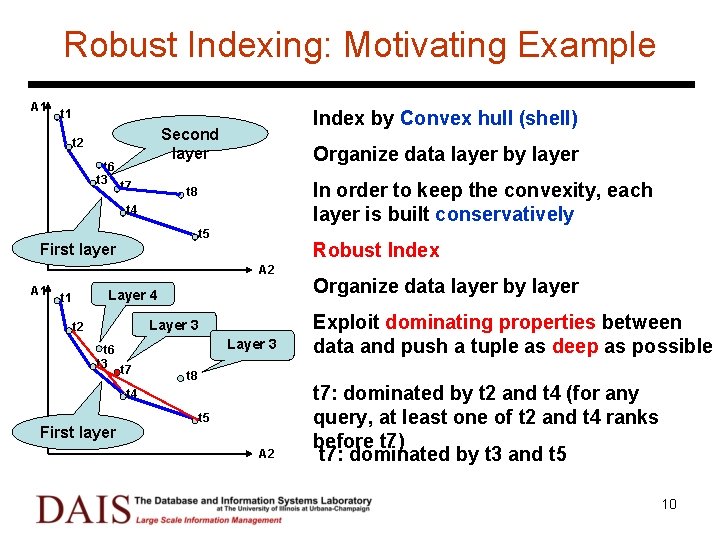
Robust Indexing: Motivating Example A 1 Index by Convex hull (shell) t 1 Second layer t 2 t 6 t 3 t 7 Organize data layer by layer In order to keep the convexity, each layer is built conservatively t 8 t 4 t 5 First layer Robust Index A 2 A 1 Layer 4 t 1 Layer 3 t 2 t 6 t 3 t 7 Layer 3 t 8 t 4 First layer t 5 A 2 Organize data layer by layer Exploit dominating properties between data and push a tuple as deep as possible t 7: dominated by t 2 and t 4 (for any query, at least one of t 2 and t 4 ranks before t 7) t 7: dominated by t 3 and t 5 10

Robust Indexing: Formal Definition • How does it work? – Offline phase • Put each tuple in its deepest layer: the minimal (best) rank of all possible linear queries – Online phase • Retrieve tuples in top-k layers • Evaluate all of them, and report top-k • What are expected? – Correctness – Less tuples in each layer than convex hull • If a tuple does not belong to top-k for any query, it will not be retrieved 11

Robust Indexing: Appealing Properties • Database Friendly – No online algorithm required – Simply use the following SQL statement Select top k * from R where layer <=k order by Frank • Space efficient – Suppose the upper bound of the value k is given (e. g. k<=100) – Only need to index those tuples in top 100 layers – Robust indexing uses the minimal space comparing with other alternatives 12

Outline • Introduction • Robust Index • Compute Robust Index – Exact Solution – Approximate Solution – Multiple Indices • Performance Study • Discussion and Conclusions 13

Robust Indexing: Algorithm Highlights • Exact Solution – Compute the deepest layer for each tuple – Complexity: • n: number of tuples • d: number of dimensions • Approximate Solution – Compute the lower bound layer for each tuple – Complexity: • Multiple Indices – Transform R to different subspaces by linear transformation – Build an index in each subspace 14

Exact Solution Task: to compute the minimal rank over all possible linear queries for tuple t L 1 A 1 L 2 L 3 L 4 t 1 t 6 t 2 t t 5 t 3 t 4 Given a query Q, with ranking function F=w 1 A 1+w 2 A 2, 0<=w 1, w 2<=1, and w 1+w 2=1 Q is one-to-one mapped to a line L e. g. A 1+2 A 2 maps to L 1 A 2 Naïve Proposal: Enumerate all possible combinations of (w 1, w 2) Not feasible since the enumerating space is infinite Alternative Solution: Only enumerate (w 1, w 2) whose corresponding line passes t and another tuple, e. g. , L 1, … , L 4 Do not consider t 3 and t 6 because the corresponding weights does not satisfy 0<=w 1, w 2<=1 15

Exact Solution, cont. L 1 A 1 L 2 L 3 L 4 Task: to compute the minimal rank over all possible linear queries for tuple t LV t 1 t 6 t 2 LH t t 5 t 3 Given a query Q, with ranking function F=w 1 A 1+w 2 A 2, 0<=w 1, w 2<=1, and w 1+w 2=1 Lv=>L 1: minimal rank is 4 (after t 1, t 2, t 3) t 4 L 1=>L 2: minimal rank is 3 (after t 2, t 3) A 2 Complexity: to sort all lines takes O(n log n), to compute minimal rank for all t, In general, L 2=>L 3: minimal rank is 4 (after t 2, t 3, t 4) L 3=>L 4: minimal rank is 3 (after t 3, t 4) L 4=>LH: minimal rank is 4 (after t 3, t 4, t 5) Minimal rank (the deepest layer) of t is 3 16

Approximate Solution A 1 I 4 I Task: to compute the lower bould of the minimal rank of tuple t IV I 3 I 2 I 1 Four regions II: dominating region, data ranked before t IV: dominated region, data ranked after t I and III? t III 4 II III 3 III 1 III 2 III A 2 Lower Bounding Theorem [Minimal ranking of t] >= card(II) + min( card(I 3+I 2+I 1), card(I 2+I 1+III 1), card(I 1+III 2), card(III 1+III 2+III 3)) Step 1: Partition regions I and III Step 2: Count cardinalities of region II and sub-regions I 1, …, I 4, III 1, …, III 4 Step 3: Match the cardinalities of the sub-regions and compute the lower bound 17

Approximate Solution, Cont. A 1 I 4 I IV I 3 L Step 2: Count cardinalities of region II and sub-regions I 1, …, I 4, III 1, …, III 4 I 2 I 1 Count the cardinality of region II? 1. All tuples in region II dominate t 2. A reversed version of skyline problem 3. Standard divide and conquer solution (details in the paper) t III 4 III 3 II III 1 III 2 III A 2 Tid A 1 A 2 t 0. 50 t -0. 50 0. 63 t 1 0. 15 0. 80 t 1 -0. 15 0. 35 t 2 0. 25 0. 55 t 2 -0. 25 0. 39 t 3 0. 40 0. 35 t 3 -0. 40 0. 49 A 1=-A 1 A 2=A 1+0. 25 A 2 Count the cardinality of region I 1? Suppose t: (a 1, a 2) Line L: A 1 + 0. 25 A 2=a 1 + 0. 25 a 2 Tuples in region I 1 satisfy -A 1 <= -a 1 A 1+0. 25 A 2 <= a 1 + 0. 25 a 2 18

Quality of the Approximate Solution • Complexity: – B: number of partitions in each subspace – n: number of tuples – d: number of dimensions • Approximate quality: – Assume data forms a uniform distribution – Each subspace is partitioned evenly – Partitioning according to the data distribution is an important and interesting future topic 19

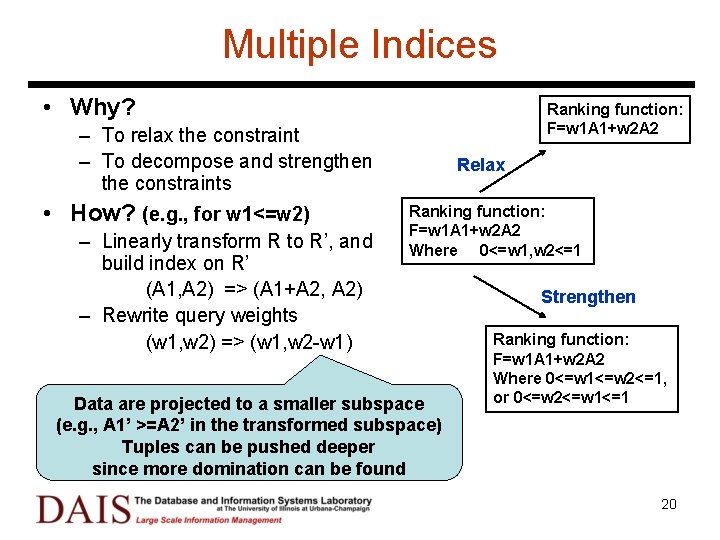
Multiple Indices • Why? Ranking function: F=w 1 A 1+w 2 A 2 – To relax the constraint – To decompose and strengthen the constraints • How? (e. g. , for w 1<=w 2) – Linearly transform R to R’, and build index on R’ (A 1, A 2) => (A 1+A 2, A 2) – Rewrite query weights (w 1, w 2) => (w 1, w 2 -w 1) Relax Ranking function: F=w 1 A 1+w 2 A 2 Where 0<=w 1, w 2<=1 Data are projected to a smaller subspace (e. g. , A 1’ >=A 2’ in the transformed subspace) Tuples can be pushed deeper since more domination can be found Strengthen Ranking function: F=w 1 A 1+w 2 A 2 Where 0<=w 1<=w 2<=1, or 0<=w 2<=w 1<=1 20

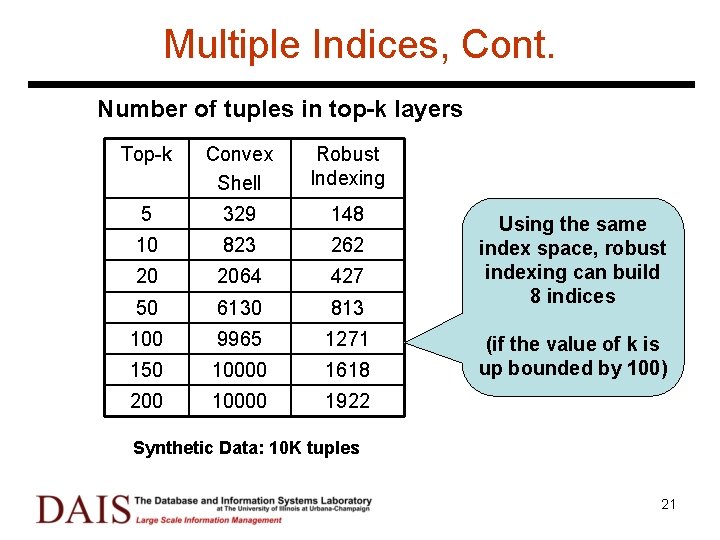
Multiple Indices, Cont. Number of tuples in top-k layers Top-k Convex Shell Robust Indexing 5 329 148 10 823 262 20 2064 427 50 6130 813 100 9965 1271 150 10000 1618 200 10000 1922 Using the same index space, robust indexing can build 8 indices (if the value of k is up bounded by 100) Synthetic Data: 10 K tuples 21

Outline • Introduction • Robust Index • Compute Robust Index – Exact Solution – Approximate Solution – Multiple Indices • Performance Study • Discussion and Conclusions 22

Performance Study • Data – Synthetic data – Real dataset (abalone 3 D, cover 3 D) • Measure – Number of tuples retrieved – Execution time not reported, but the robust indexing is expected to be even better • Approaches for comparison – Onion (convex shell) – PREFER – Approximate Robust Indexing (App. RI), #partition=10 23

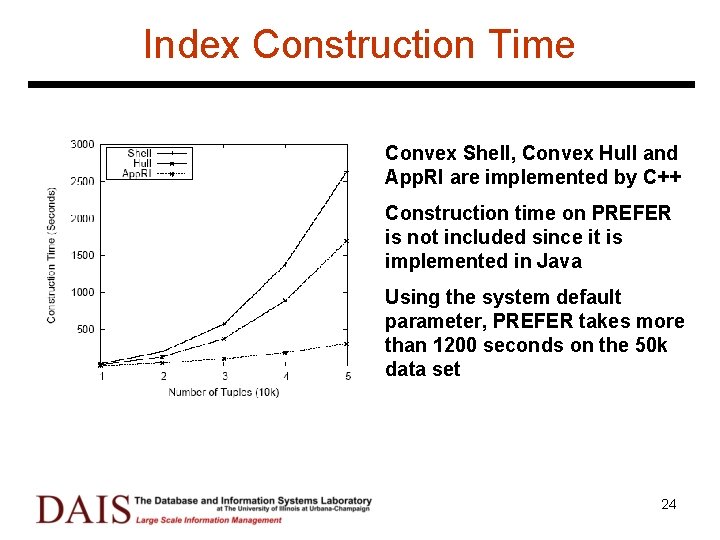
Index Construction Time Convex Shell, Convex Hull and App. RI are implemented by C++ Construction time on PREFER is not included since it is implemented in Java Using the system default parameter, PREFER takes more than 1200 seconds on the 50 k data set 24

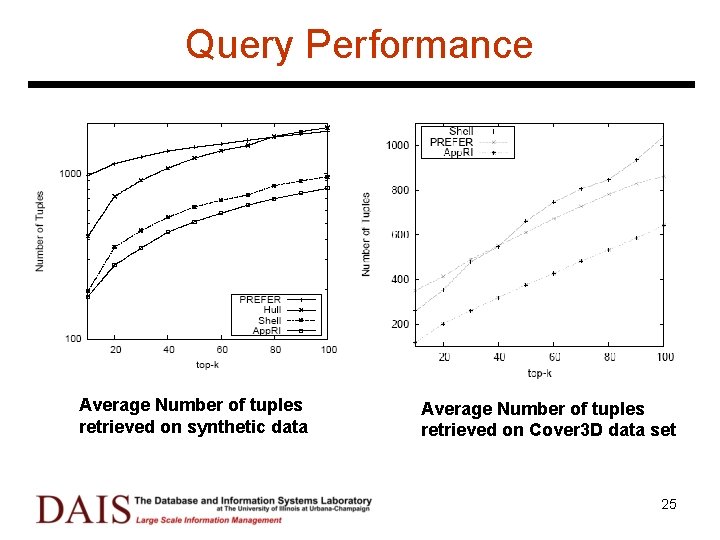
Query Performance Average Number of tuples retrieved on synthetic data Average Number of tuples retrieved on Cover 3 D data set 25

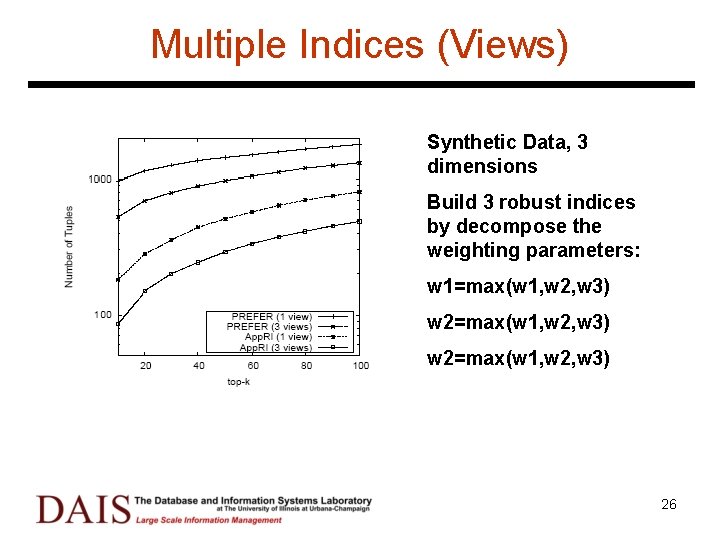
Multiple Indices (Views) Synthetic Data, 3 dimensions Build 3 robust indices by decompose the weighting parameters: w 1=max(w 1, w 2, w 3) w 2=max(w 1, w 2, w 3) 26

Discussion and Conclusions • Strength – Easy to integrate with current DBMS – Good query performance – Practical construction complexity • Limitation – Online index maintenance is expensive (some weaker maintaining strategies available) – Indexing high dimensional data remains a challenging problem 27