Towards Practical and Robust Labeled Pattern Matching in

Towards Practical and Robust Labeled Pattern Matching in Trillion-Edge Graphs Tahsin Reza, Christine Klymko, Matei Ripeanu, Geoffrey Sanders, Roger Pearce 1

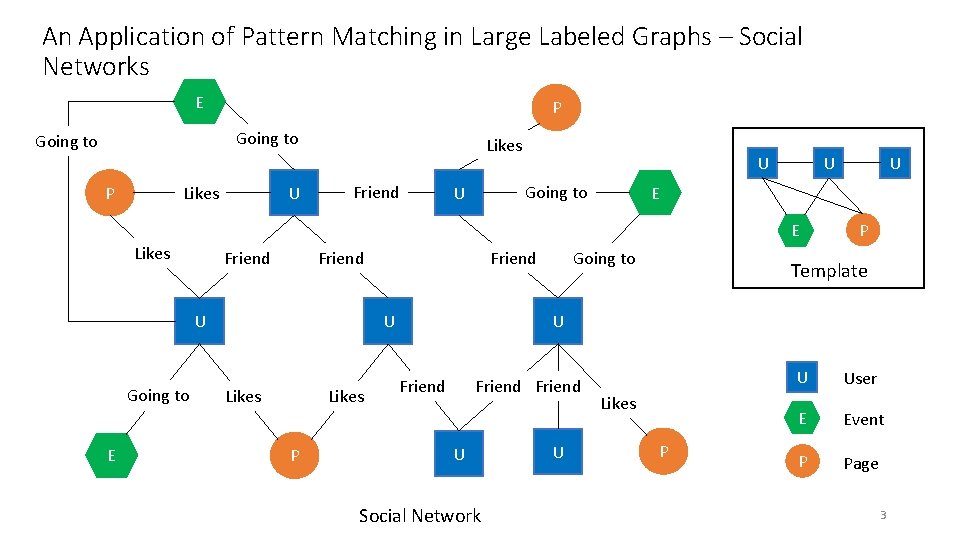
An Application of Pattern Matching in Large Labeled Graphs – Social Networks E P Going to P U Likes Friend U U Going to E [Ching 2015] Likes P Likes U Social Network U U E Identify. Likesall the users who have at least one Friend Going to friend x and x has at least one friend y, and both x and Uy went to the. U same event. U and like the same page Friend Going to U P E P Template U User E Event P Page 2

An Application of Pattern Matching in Large Labeled Graphs – Social Networks E P Going to U Likes P Likes Friend U Going to U U E E Likes Friend U Going to E Friend U Likes P U Going to P Template U Friend U Social Network U Likes P U User E Event P Page 3

An Application of Pattern Matching in Large Labeled Graphs – Social Networks E P Going to U Likes P Likes Friend U Going to U U E E Likes Friend U Going to E Friend U Likes P U Going to P Template U Friend U Social Network U Likes P U User E Event P Page 4

Highlights Graph pruning is an effective solution for Pattern Matching § Input reduction by orders of magnitude, 103 – 107 times smaller § Scales well with graph, 1012 edges and platform size, 103 cores § Exact solutions for some classes of templates § No assumption about the graph and no preprocessing required 1. 1 trillion edges on 256 nodes / 6, 144 cores in under two minutes 5

The Many ‘Faces’ of Pattern Matching Match The problem solved § Exact or inexact § Enumeration of matches § Isomorphism, homomorphism § Match counting § Induced or noninduced § Set of matching vertices and edges § Topology only and/or label-based § Match exists or not ▫ Vertex and/or Edge label § … Input § Directed or undirected § Cyclic or acyclic [Ullman 1976] 6

The Many ‘Faces’ of Pattern Matching Match The problem solved § Exact or inexact § Enumeration of matches § Isomorphism, homomorphism § Match counting § Induced or noninduced § Set of matching vertices and edges § Topology only and/or label-based § Match exists or not ▫ Vertex and/or Edge label § … Input § Directed or undirected § Cyclic or acyclic 7

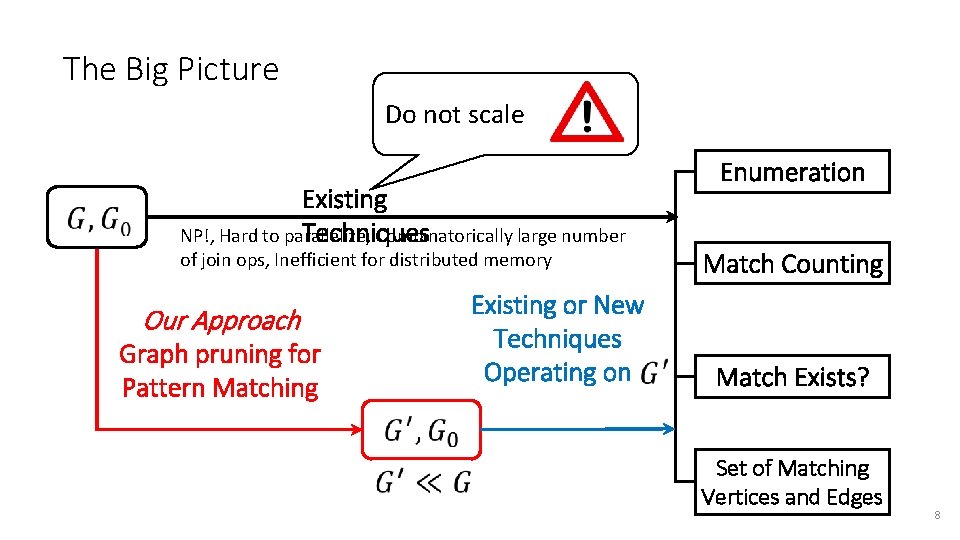
The Big Picture Do not scale Existing Techniques NP!, Hard to parallelize, Combinatorically large number of join ops, Inefficient for distributed memory Our Approach Graph pruning for Pattern Matching Existing or New Techniques Operating on Enumeration Match Counting Match Exists? Set of Matching Vertices and Edges 8

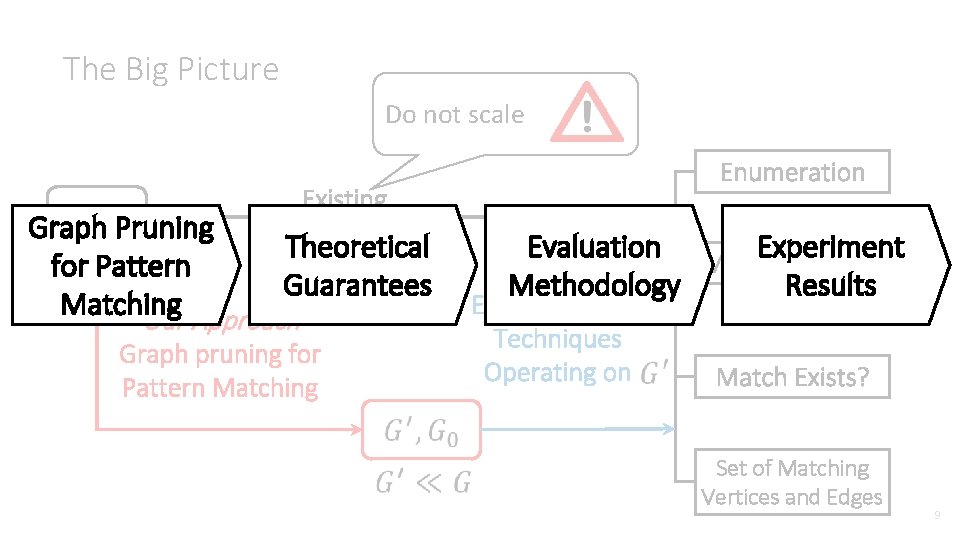
The Big Picture Do not scale Existing Techniques Graph Pruning Theoretical for Pattern Guarantees Matching Our Approach Graph pruning for Pattern Matching Enumeration Experiment Evaluation Match Counting Results Methodology Existing or New Techniques Operating on Match Exists? Set of Matching Vertices and Edges 9

Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Design Objectives § Supports a rich set of pattern matching scenarios § 100% recall, i. e. , no false negatives § High precession, i. e. , low false positives § Ability to process large graphs, e. g. , 109 – 1012 edges § Fast time to solution, human in the loop ▫ ▫ ▫ Horizontal scalability, thousands of nodes Leverage existing frameworks, e. g. , Giraph, Graph. Lab, Havoq. GT ― Vertex-centric algorithms Low memory and communication overhead 10

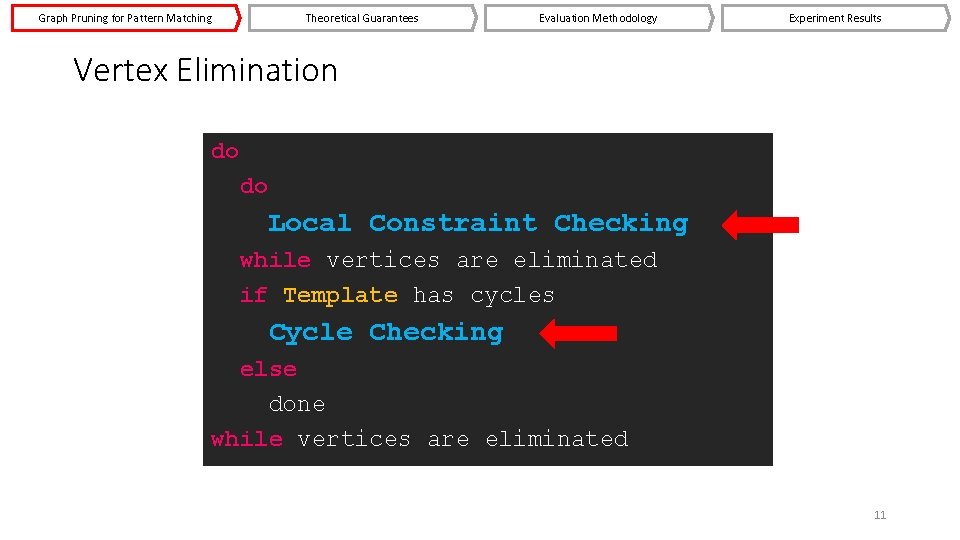
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated 11

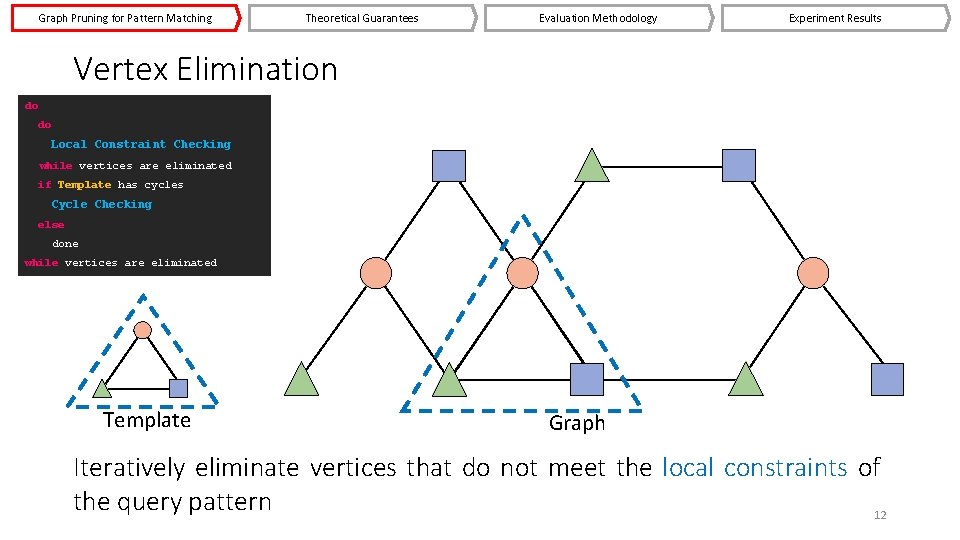
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Iteratively eliminate vertices that do not meet the local constraints of the query pattern 12

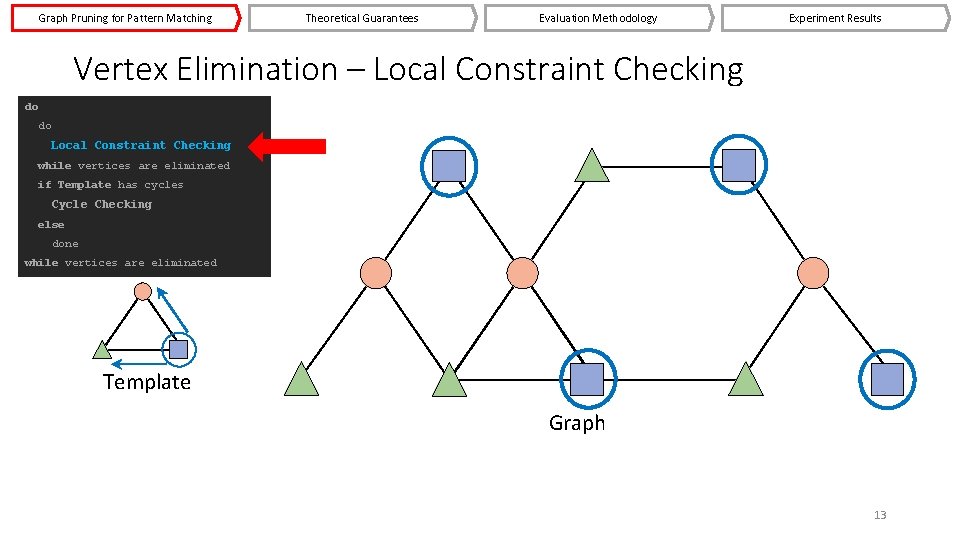
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Local Constraint Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph 13

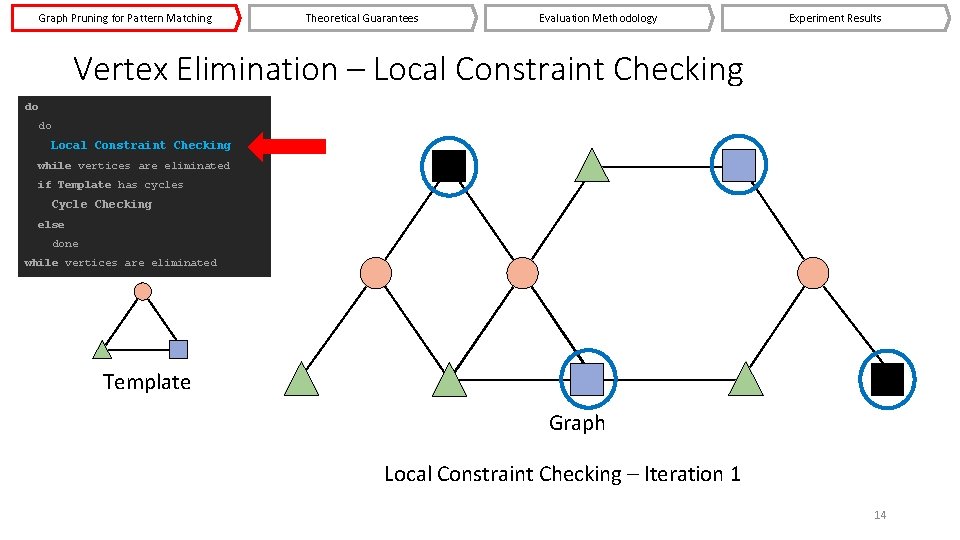
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Local Constraint Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Local Constraint Checking – Iteration 1 14

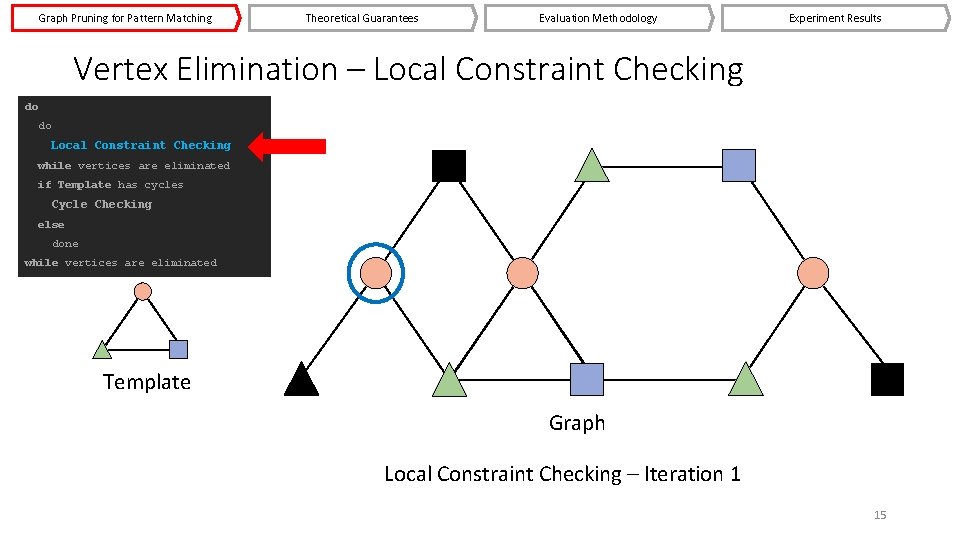
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Local Constraint Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Local Constraint Checking – Iteration 1 15

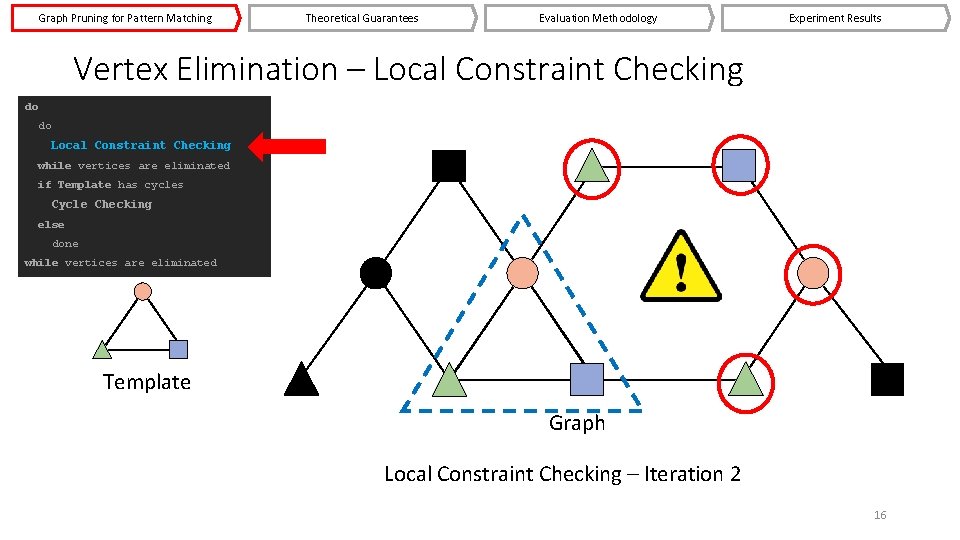
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Local Constraint Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Local Constraint Checking – Iteration 2 16

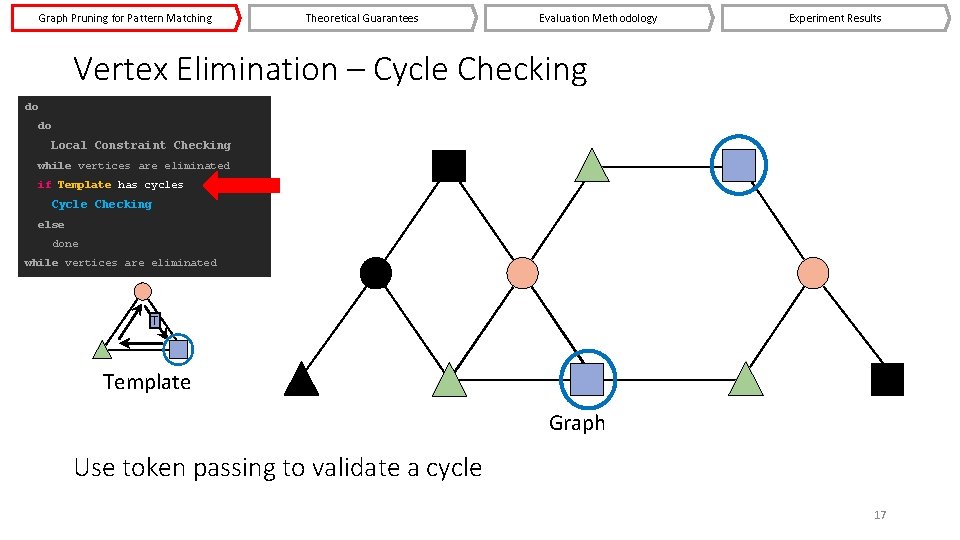
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Cycle Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated T Template Graph Use token passing to validate a cycle 17

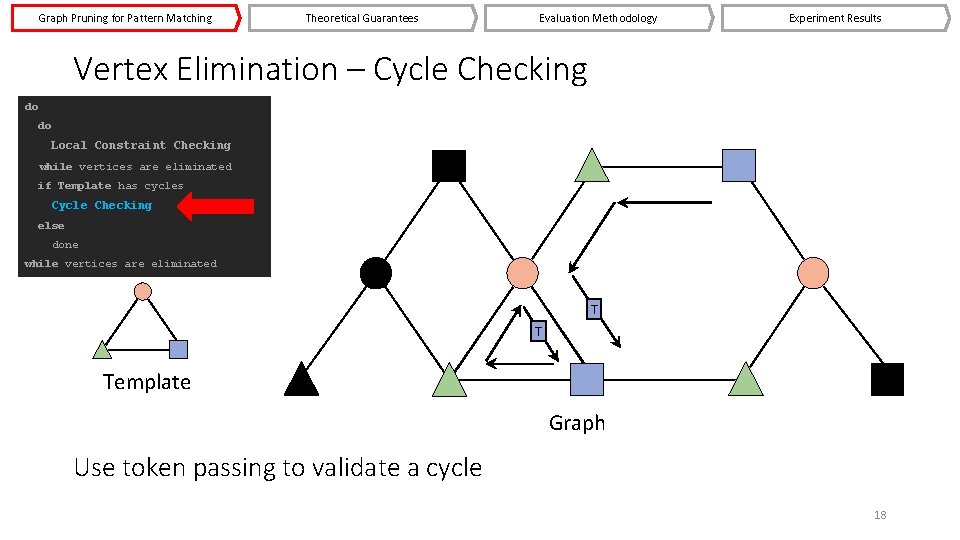
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Cycle Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated T T Template Graph Use token passing to validate a cycle 18

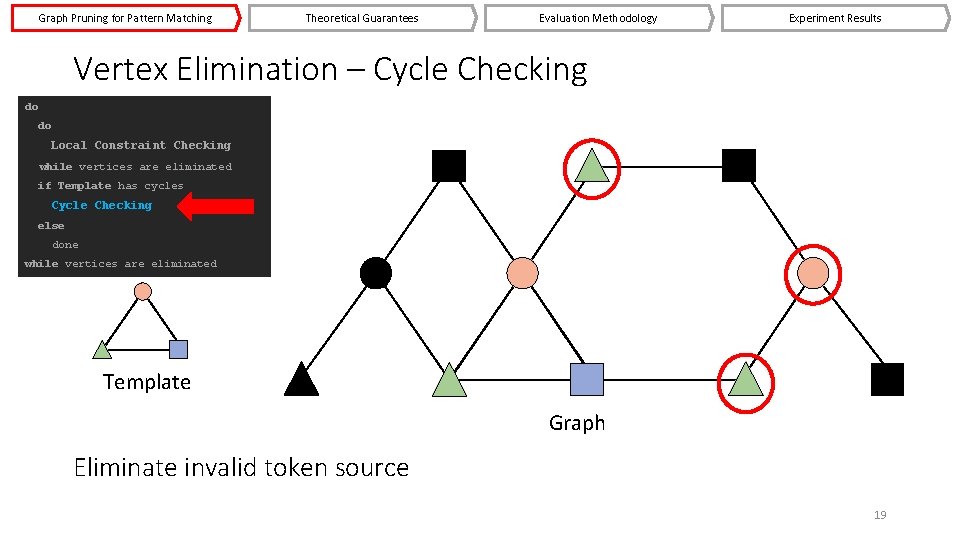
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Cycle Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Eliminate invalid token source 19

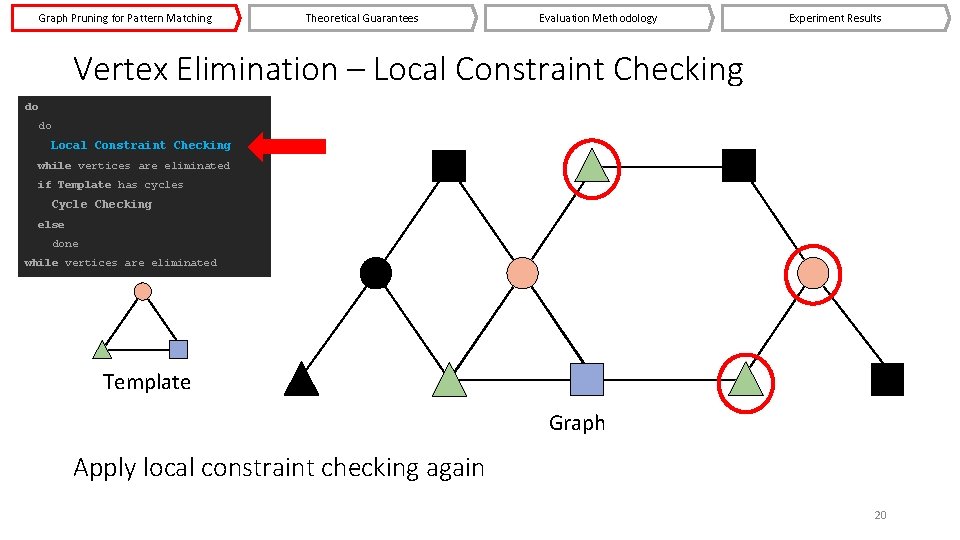
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination – Local Constraint Checking do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Apply local constraint checking again 20

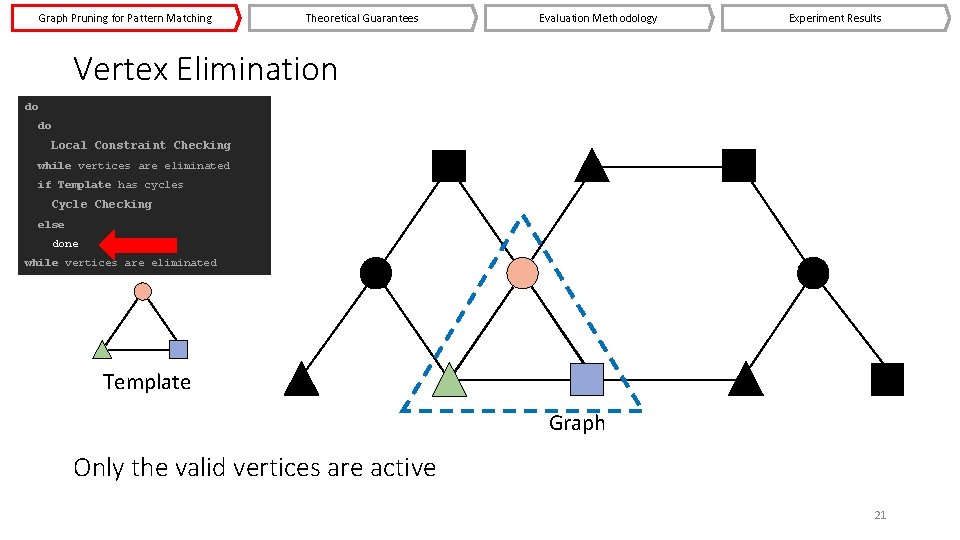
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Vertex Elimination do do Local Constraint Checking while vertices are eliminated if Template has cycles Cycle Checking else done while vertices are eliminated Template Graph Only the valid vertices are active 21

Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Theoretical Guarantees Precise solution guarantee § The pruned graph only contains vertices that participate in a match Assumptions about the template § Undirected § Acyclic or edge-monocyclic § Unique vertex labels Acyclic Edge-monocyclic 22

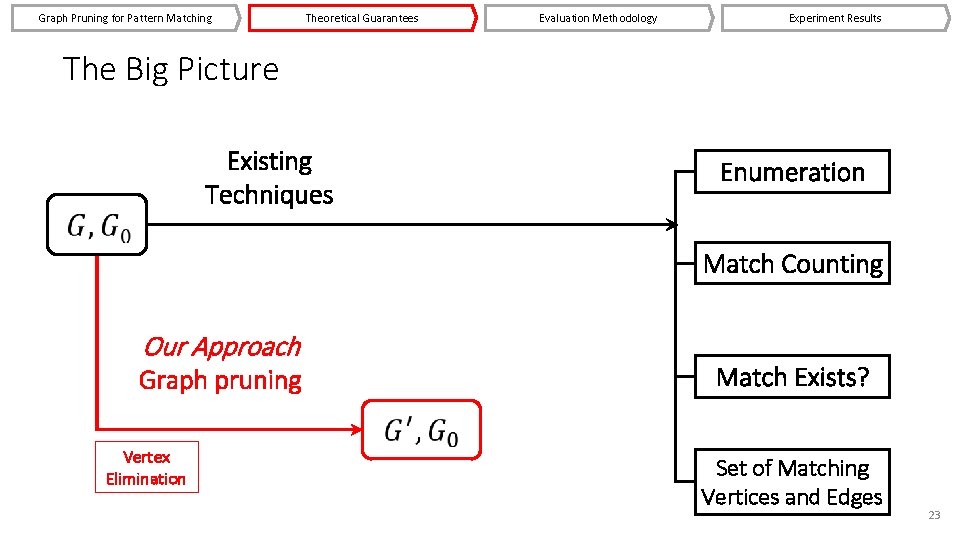
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results The Big Picture Existing Techniques Enumeration Match Counting Our Approach Graph pruning Vertex Elimination Match Exists? Set of Matching Vertices and Edges 23

Graph Pruning for Pattern Matching Theoretical Guarantees The Big Picture Evaluation Methodology could be 107 times smaller than Existing Techniques Our Approach Enumeration Existing or New Techniques Operating on Match Counting Match Exists? Graph pruning Vertex Elimination Experiment Results Conditions – undirected, acyclic or edgemonocyclic, unique labels Set of Matching Vertices and Edges 24

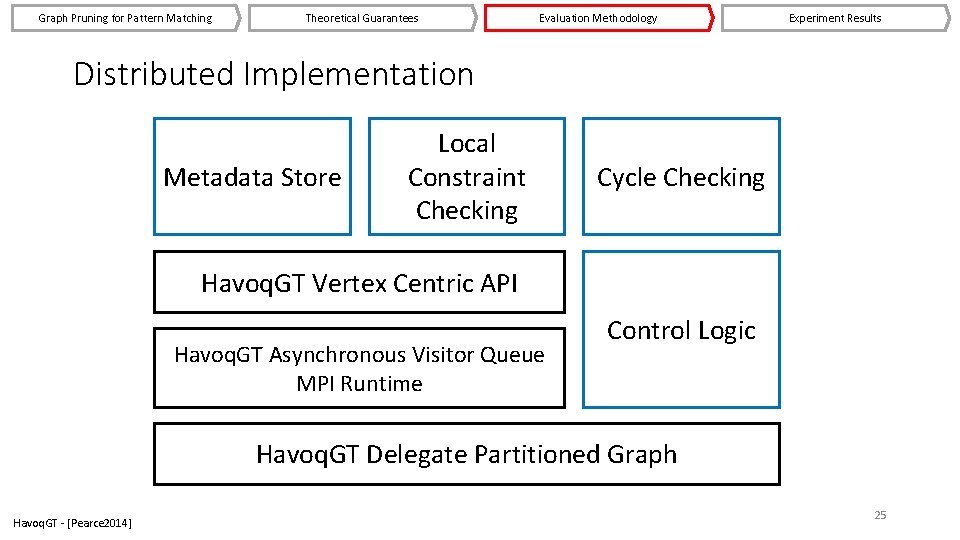
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Distributed Implementation Metadata Store Local Constraint Checking Cycle Checking Havoq. GT Vertex Centric API Havoq. GT Asynchronous Visitor Queue MPI Runtime Control Logic Havoq. GT Delegate Partitioned Graph Havoq. GT - [Pearce 2014] 25

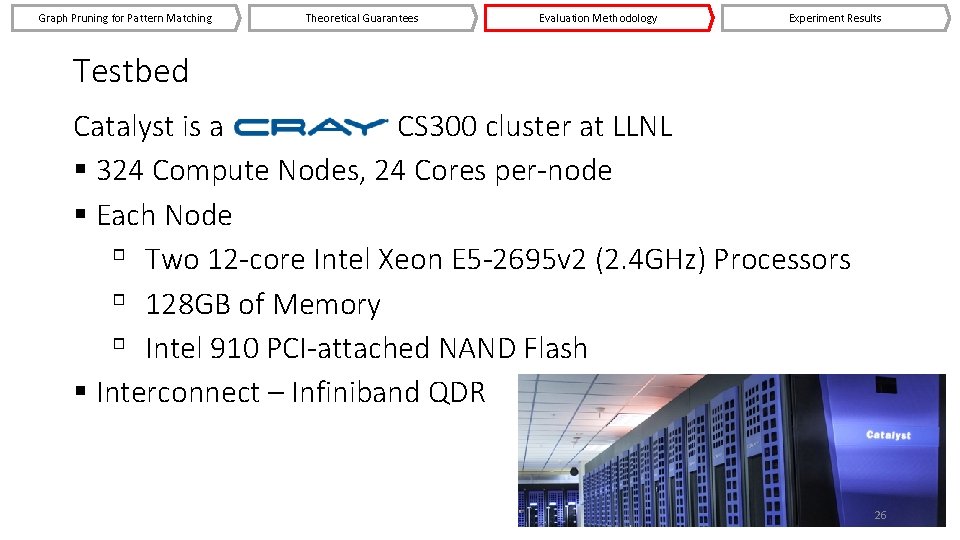
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Testbed Catalyst is a CS 300 cluster at LLNL § 324 Compute Nodes, 24 Cores per-node § Each Node ▫ Two 12 -core Intel Xeon E 5 -2695 v 2 (2. 4 GHz) Processors ▫ 128 GB of Memory ▫ Intel 910 PCI-attached NAND Flash § Interconnect – Infiniband QDR 26

Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Evaluation Methodology § Strong and weak scaling experiments § Performance metric – search time for a single template ▫ Pruning factor 27

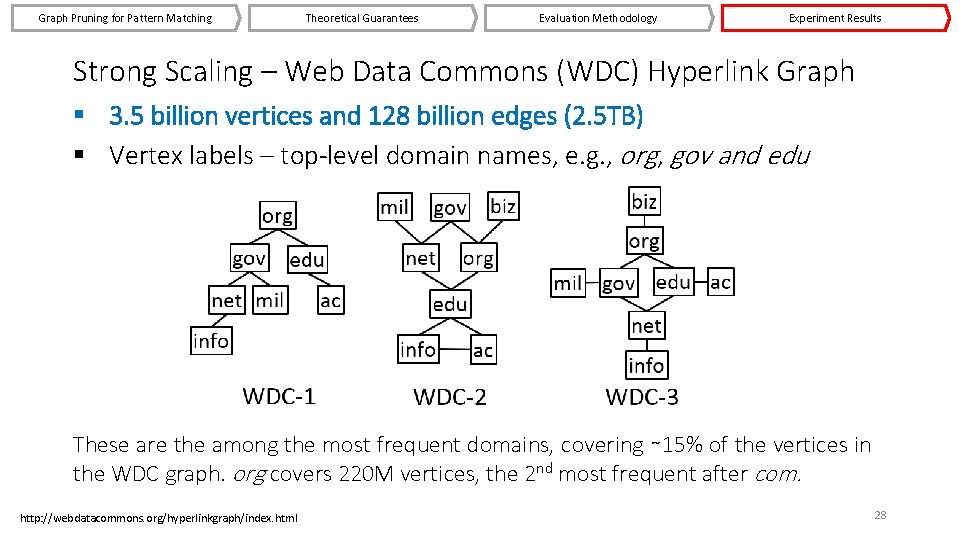
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Strong Scaling – Web Data Commons (WDC) Hyperlink Graph § 3. 5 billion vertices and 128 billion edges (2. 5 TB) § Vertex labels – top-level domain names, e. g. , org, gov and edu These are the among the most frequent domains, covering ∼ 15% of the vertices in the WDC graph. org covers 220 M vertices, the 2 nd most frequent after com. http: //webdatacommons. org/hyperlinkgraph/index. html 28

Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Strong Scaling Experiments # Compute nodes Template 29

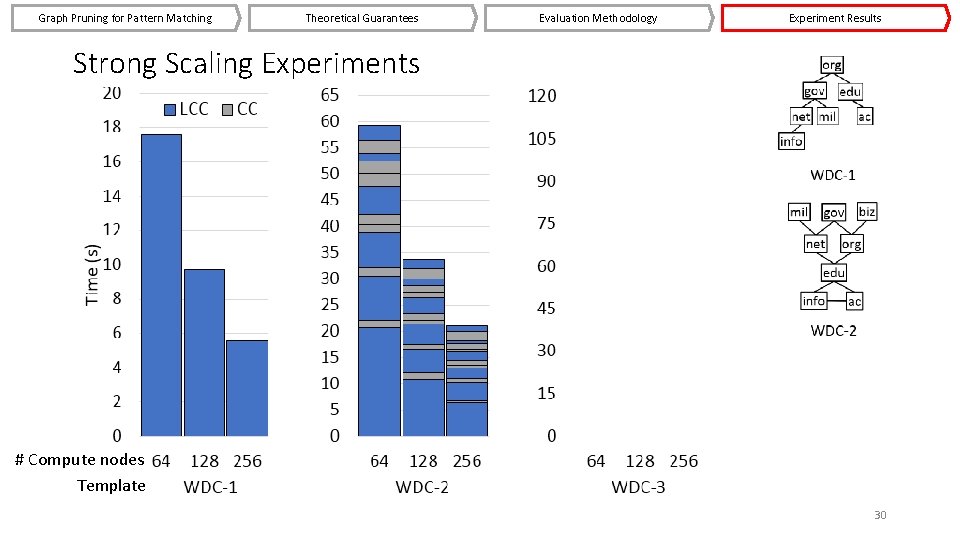
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Strong Scaling Experiments # Compute nodes Template 30

Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Strong Scaling Experiments Good scaling for cyclic and acyclic templates § LCC shows near perfect strong scaling § CC is the bottleneck ― High degree vertices § # Compute nodes Template 31

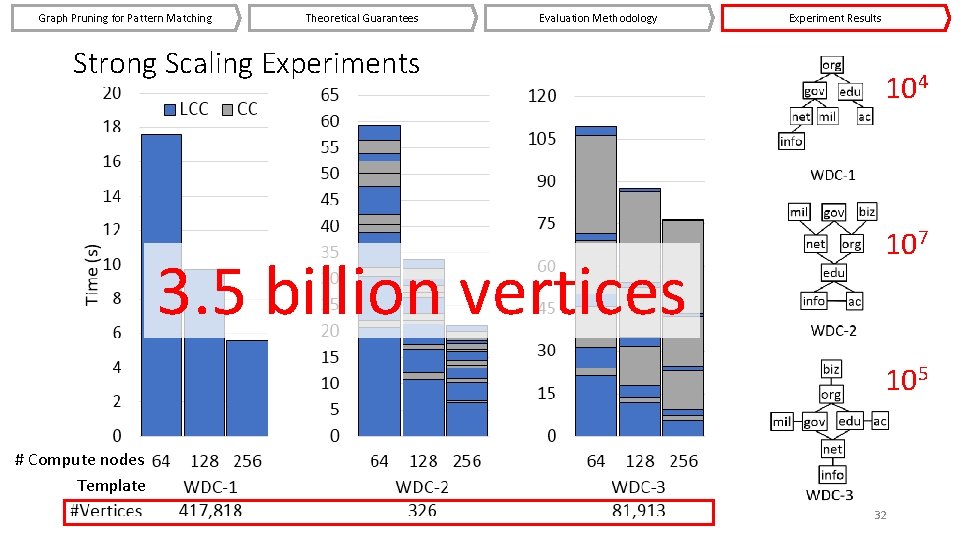
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Strong Scaling Experiments 3. 5 billion vertices Experiment Results 104 107 105 # Compute nodes Template 32

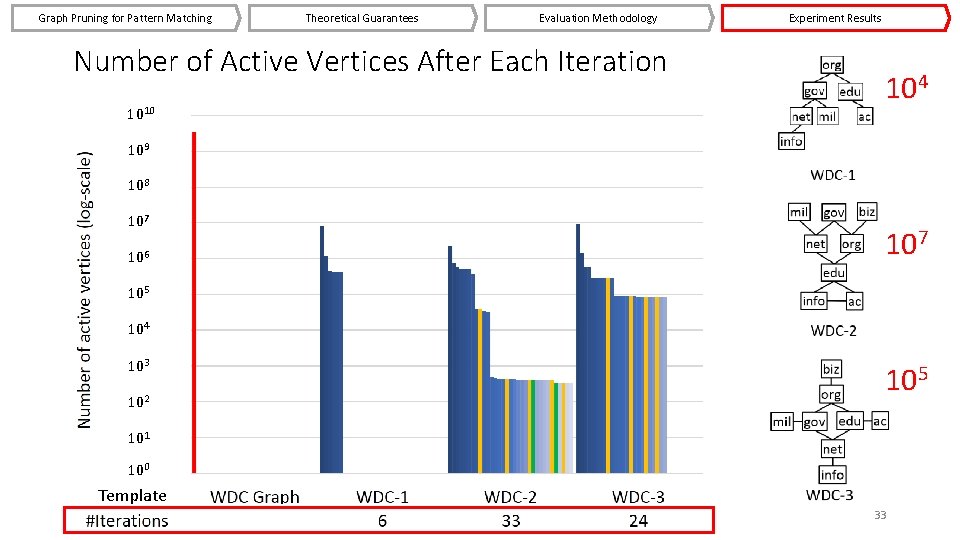
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Number of Active Vertices After Each Iteration 1010 Experiment Results 104 109 108 107 106 107 105 104 103 102 105 101 100 Template 33

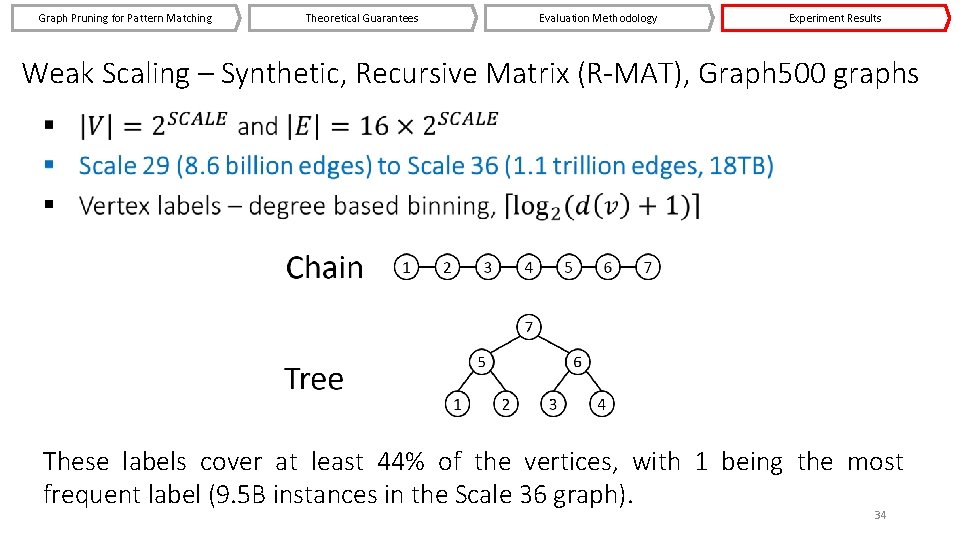
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Weak Scaling – Synthetic, Recursive Matrix (R-MAT), Graph 500 graphs These labels cover at least 44% of the vertices, with 1 being the most frequent label (9. 5 B instances in the Scale 36 graph). 34

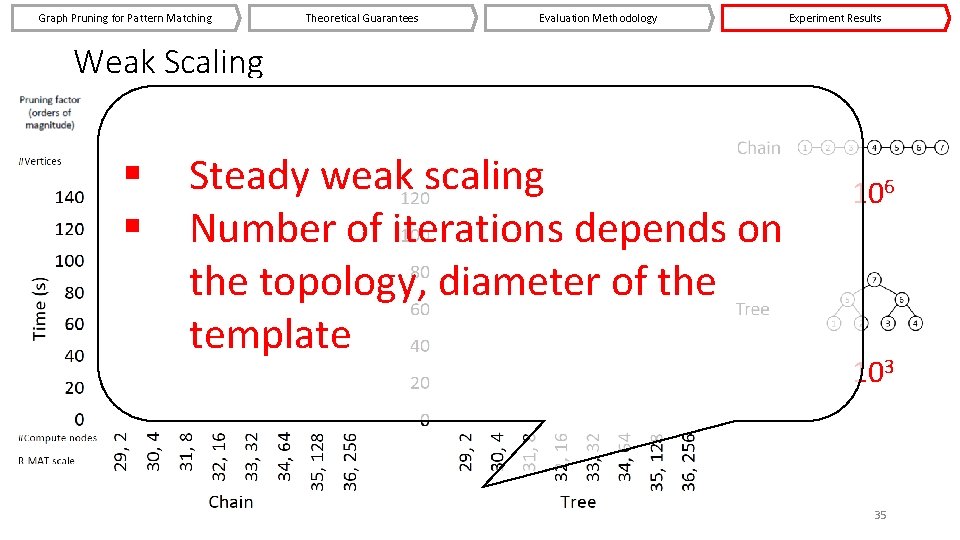
Graph Pruning for Pattern Matching Theoretical Guarantees Evaluation Methodology Experiment Results Weak Scaling § § Steady weak scaling Number of iterations depends on the topology, diameter of the template 106 103 35

Takeaways § Graph pruning is an enabler for pattern matching on very large graphs - computationally intractable today § Pruning algorithms - low complexity, highly parallelizable and scalable § For some problems, pruning leads to the solution Tahsin Reza – treza@ece. ubc. ca computation. llnl. gov/casc netsyslab. ece. ubc. ca 36

Backup Slides

Large-scale Graph Processing Frameworks Havoq. GT PGX. D 38

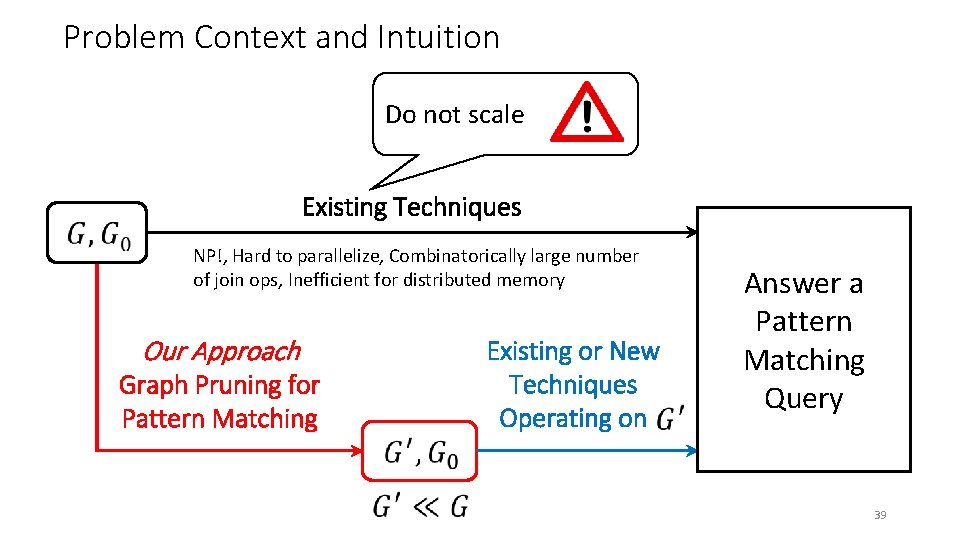
Problem Context and Intuition Do not scale Existing Techniques NP!, Hard to parallelize, Combinatorically large number of join ops, Inefficient for distributed memory Our Approach Graph Pruning for Pattern Matching Existing or New Techniques Operating on Answer a Pattern Matching Query 39

Practical Relevance of Processing at Billion/Trillion Scale § Web scale, Social media scale and Brain Scale – 109 to 1012 edges § Web Data Commons ‘hyperlink’ graph – 128 billion edges § Facebook ‘users’ graph have more than one trillion edges § Lehigh University Benchmark (LUBM) RDF graph consists of 1. 08 trillion triples § Connectomics / Human Brain Network – 100+ billion vertices, 100+ trillion edges https: //www. w 3. org/wiki/Large. Triple. Stores 40

Existing Techniques and their Limitations § Search-and-Join due to Ullman ▫ Possible join operations is combinatorically large ▫ Large intermediate matches ▫ Backtracking algorithm – difficult to parallelize ▫ High message complexity § Indexing frequent graph structures ▫ The growth of the index size may be super-linear relative to the size of the graph § Color coding 41

Foundational work for subgraph isomorphism is based on the tree-search approach introduced by Ullman [6]. Most methods for exact (as well as inexact) matching found in the literature follow the tree-search approach due to Ullman and often attempt to improve upon Ullman’s algorithm in terms of join order and pruning strategies. The widely known VF 2 algorithm by Cordella et al. offres signifiant improvisent over Ullman’s technique [10]. VF 2 improves time complexity over Ullman’s algorithm from O(V !V 2) to O(V !V ) and space complexity from O(V 3) to O(V), where V is the number of vertices in the background graph. The algorithm uses a heuristic that is based on the analysis of the vertices adjacent to vertices that have been included in a partial solution. The VF 2 algorithm is known to be robust and perform better than most proposed techniques and consecutively has been included in the popular Boost Graph Library (BGL) [11].

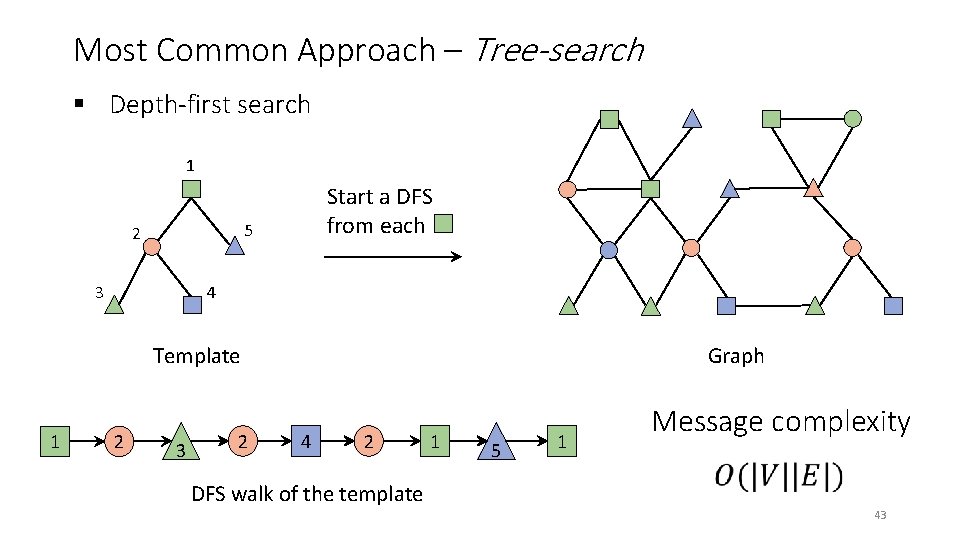
Most Common Approach – Tree-search § Depth-first search 1 Start a DFS from each 5 2 4 3 Template 1 2 3 2 Graph 4 2 DFS walk of the template 1 5 1 Message complexity 43

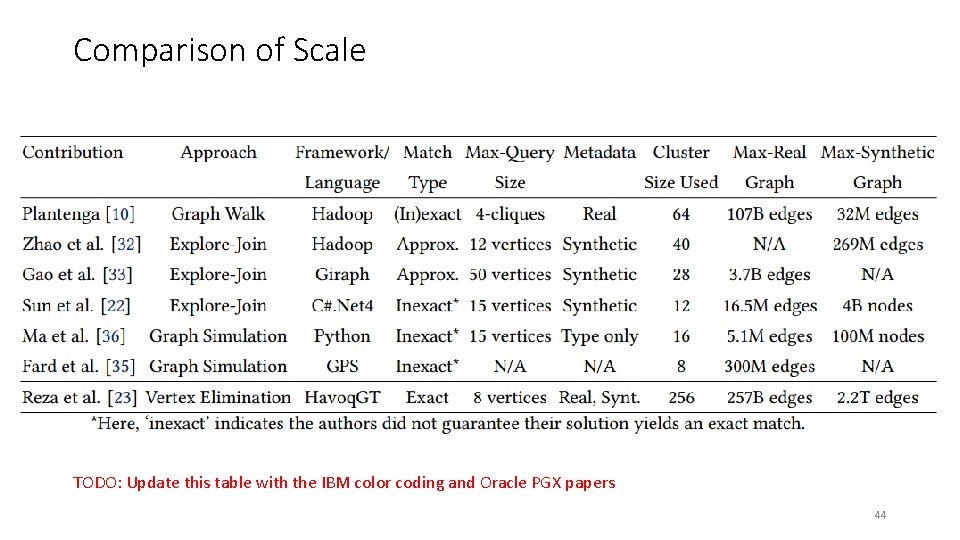
Comparison of Scale TODO: Update this table with the IBM color coding and Oracle PGX papers 44

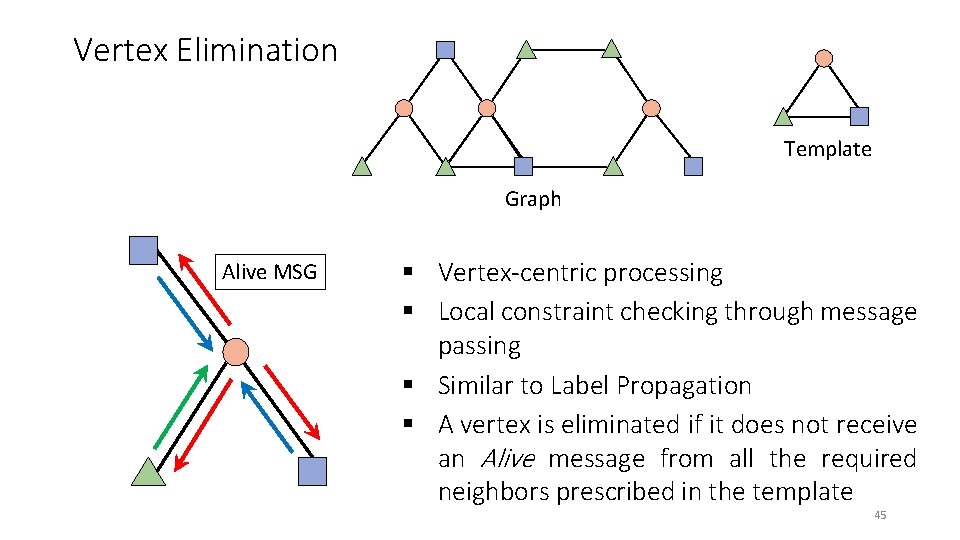
Vertex Elimination Template Graph Alive MSG § Vertex-centric processing § Local constraint checking through message passing § Similar to Label Propagation § A vertex is eliminated if it does not receive an Alive message from all the required neighbors prescribed in the template 45

Advantages over conventional Tree-search approaches 46

Unrolled Cycles / Non Edge-monocyclic template (a) template (b) template (c) Would lead to false positives 47

Scope, Complexity and Theoretical Guarantees § Undirected graphs, Edge-monocyclic patterns, Unique vertex labels Edge-monocyclic Not edge-monocyclic § Prove that the resulting pruned graph only contains vertices that participate in a match, no false positives § For more general templates the pruned list is a superset 48

Theoretical Guarantees Assumptions § Graph and pattern are undirected § Pattern is edge-monocyclic § Pattern has unique vertex labels Edge-monocyclic Not edge-monocyclic Unique vertex labels Repeating vertex labels Guarantees § The pruned graph only contains vertices that participate in a match and no false positive exists 49

Theoretical Guarantees Precise solution guarantee § The pruned graph only contains vertices that participate in a match Assumptions about the template § Undirected § Acyclic or edge-monocyclic § Unique vertex labels Acyclic Edge-monocyclic 50

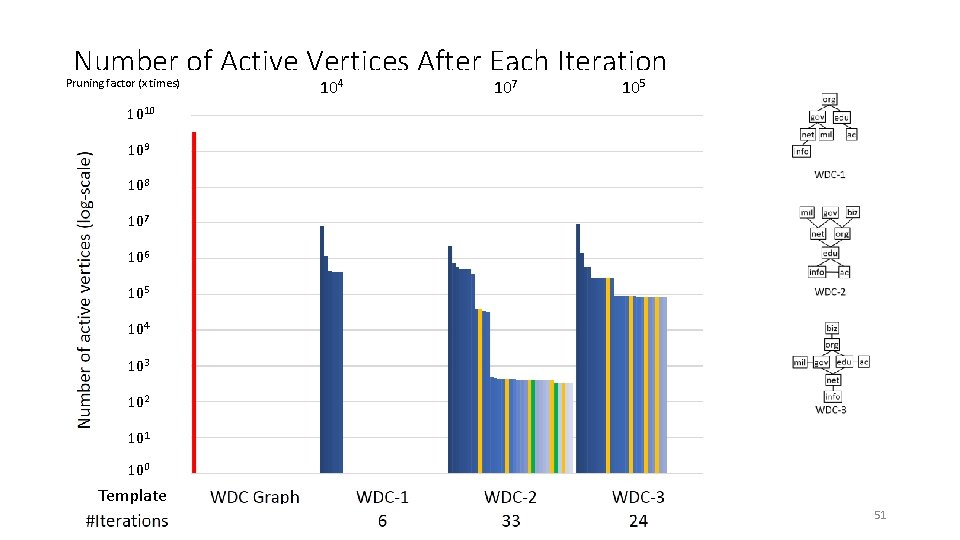
Number of Active Vertices After Each Iteration Pruning factor (x times) 104 107 105 1010 109 108 107 106 105 104 103 102 101 100 Template 51

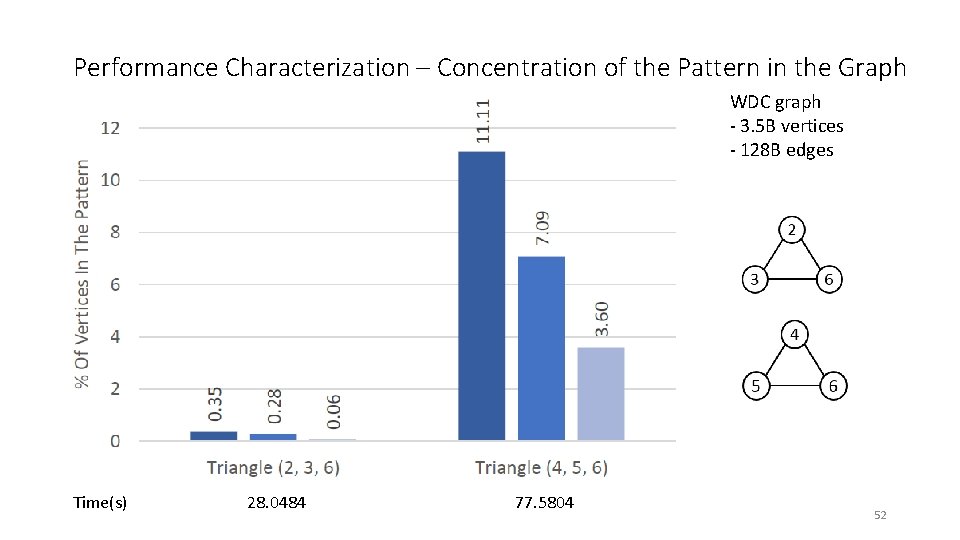
Performance Characterization – Concentration of the Pattern in the Graph WDC graph - 3. 5 B vertices - 128 B edges Time(s) 28. 0484 77. 5804 52

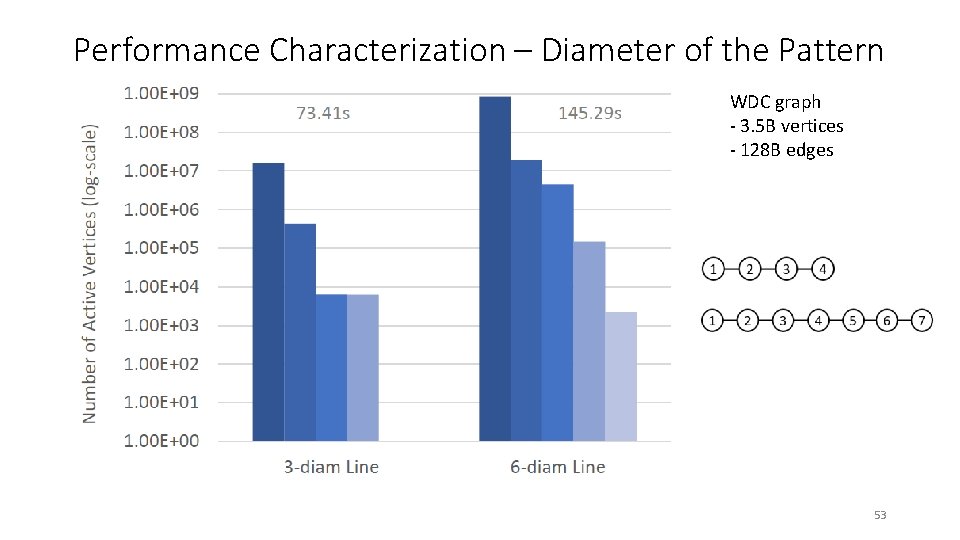
Performance Characterization – Diameter of the Pattern WDC graph - 3. 5 B vertices - 128 B edges 53

Graph 500, June 2017 3 DOE/N IBM NSA/L LNL Sequoi a 6 ALCF Mira 8192 partiti on IBM Blue. G Custo Lawre Liverm USA ene/Q, m nce ore, Power Liverm CA BQC ore 16 C Nation 1. 60 al GHz Labora tory IBM - 5 D Blue. Ge torus ne/Q, Power BQC 16 C 1. 60 GHz DOE/A Argonn USA LCF e Nation al Labora tory 2012 Scienti Gover 98304 15728 fic nment 64 Resear ch Scientif Govern 8192 ic ment Compu ting 15728 Custo 41 60 m gigaby tes 131072 16 Custo gigabyt m es 23751 368. 7 63897 secon 60 ds Watts 36 3556. 7 963. 76 3 second s 54

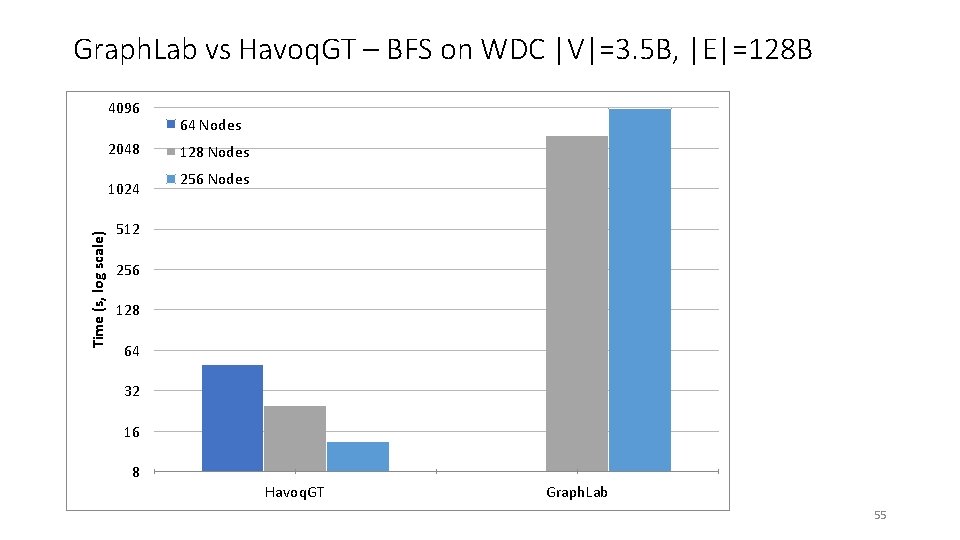
Graph. Lab vs Havoq. GT – BFS on WDC |V|=3. 5 B, |E|=128 B 4096 2048 Time (s, log scale) 1024 64 Nodes 128 Nodes 256 Nodes 512 256 128 64 32 16 8 Havoq. GT Graph. Lab 55

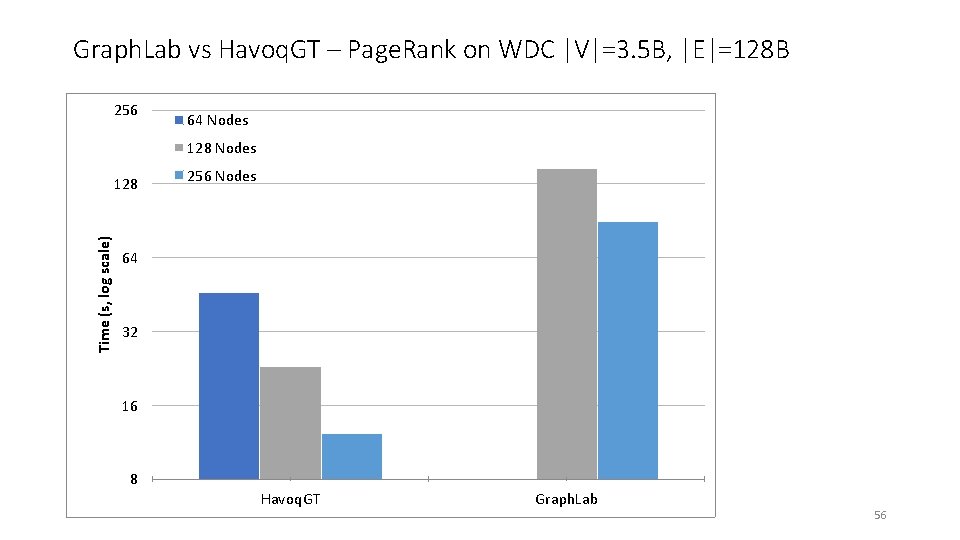
Graph. Lab vs Havoq. GT – Page. Rank on WDC |V|=3. 5 B, |E|=128 B 256 64 Nodes 128 Nodes Time (s, log scale) 128 256 Nodes 64 32 16 8 Havoq. GT Graph. Lab 56

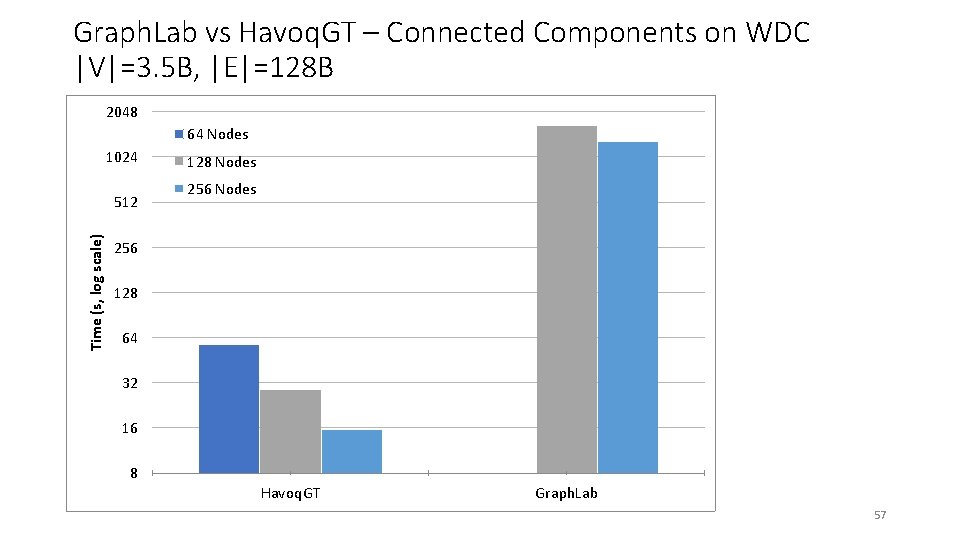
Graph. Lab vs Havoq. GT – Connected Components on WDC |V|=3. 5 B, |E|=128 B 2048 64 Nodes 1024 Time (s, log scale) 512 128 Nodes 256 128 64 32 16 8 Havoq. GT Graph. Lab 57

Extending Functionality Match § Exact or inexact § Isomorphism, homomorphism The problem solved § Enumeration of matches § Match counting § Induced or noninduced templates § Set of matching vertices and edges § Topology only and/or label-based § Match exists or not ▫ Vertex and/or Edge label § … Input graph/pattern § Directed or undirected § Cyclic or acyclic Infrastructure for edge elimination 58

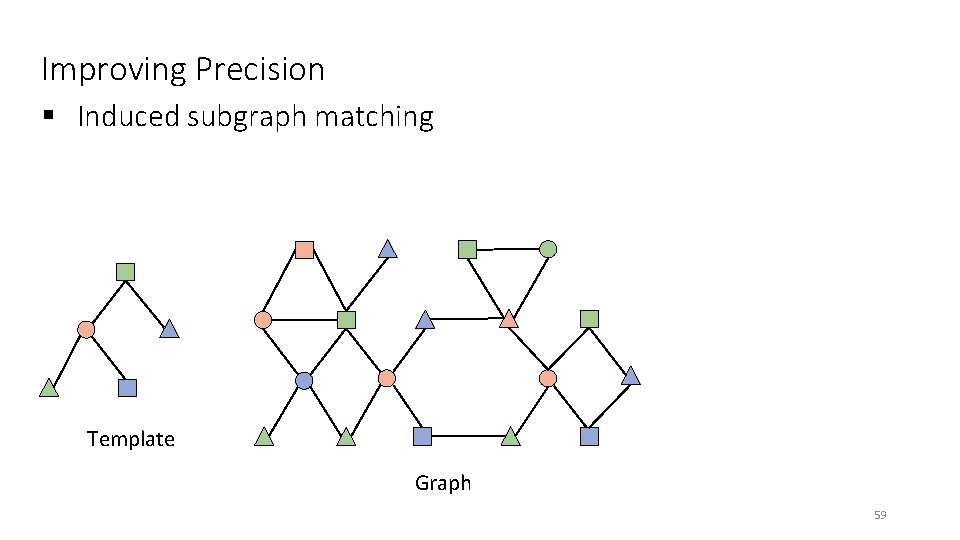
Improving Precision § Induced subgraph matching Template Graph 59

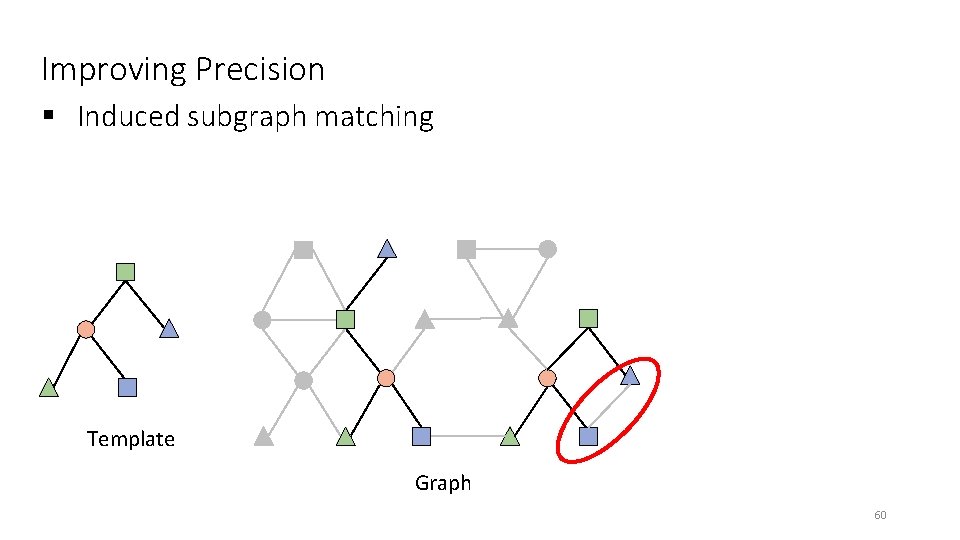
Improving Precision § Induced subgraph matching Template Graph 60

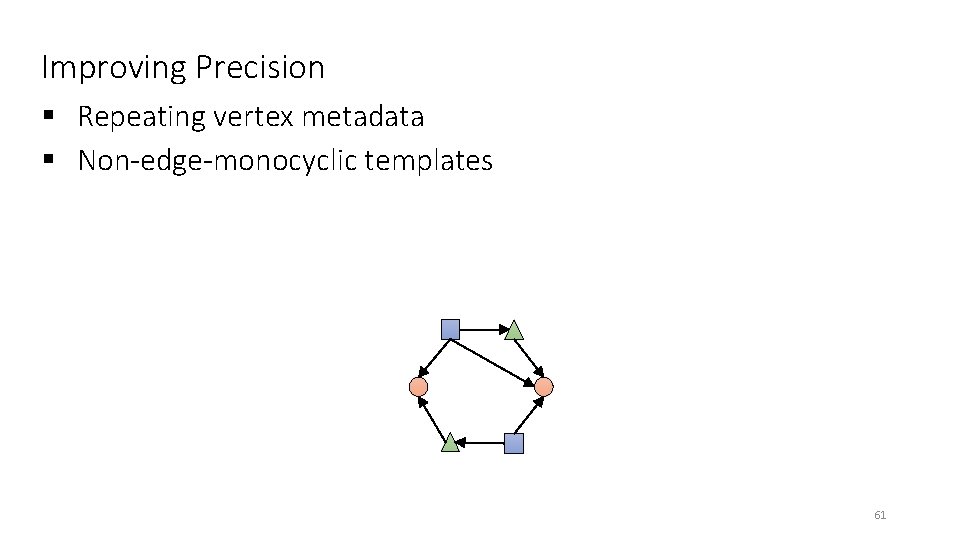
Improving Precision § Repeating vertex metadata § Non-edge-monocyclic templates 61