Towards a Theory of DataIndependent Memory Hard Functions

Towards a Theory of Data-Independent Memory Hard Functions Jeremiah Blocki (Purdue) Joël Alwen (IST Austria) Krzysztof Pietrzak (IST Austria) Real World Crypto 2017

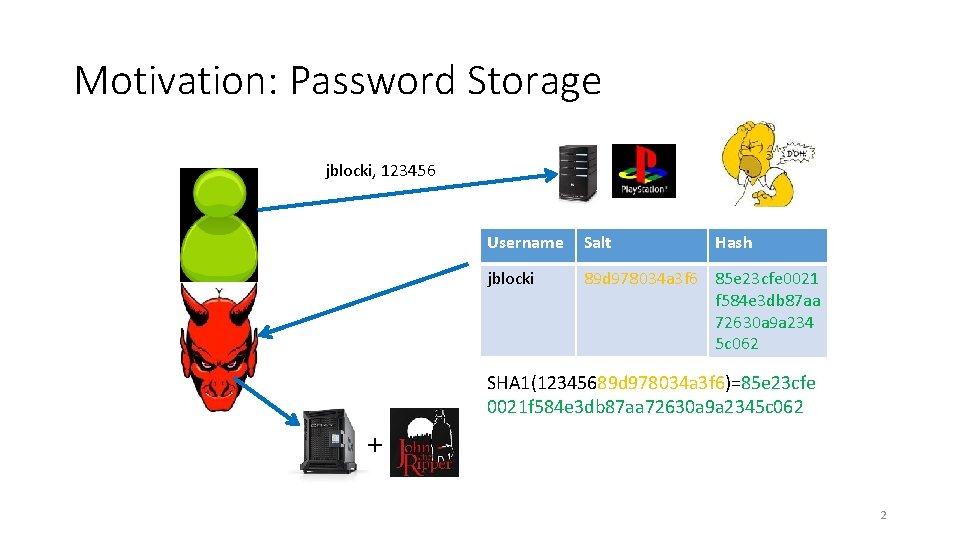
Motivation: Password Storage jblocki, 123456 Username Salt Hash jblocki 89 d 978034 a 3 f 6 85 e 23 cfe 0021 f 584 e 3 db 87 aa 72630 a 9 a 234 5 c 062 SHA 1(12345689 d 978034 a 3 f 6)=85 e 23 cfe 0021 f 584 e 3 db 87 aa 72630 a 9 a 2345 c 062 + 2

Offline Attacks: A Common Problem • Password breaches at major companies have affected millions of users.

Offline Attacks: A Common Problem • Password breaches at major companies have affected millions of users.

A Dangerous Problem $2, 400 on Amazon

Goal: Moderately Expensive Hash Function Fast on PC and Expensive on ASIC?

Memory Costs: Equitable Across Architectures

Outline • Motivation • Data Independent Memory Hard Functions (i. MHFs) • Graph Pebbling • Measuring Pebbling Costs • Desiderata • Attacks on i. MHF Constructions • Constructing i. MHFs • Open Questions

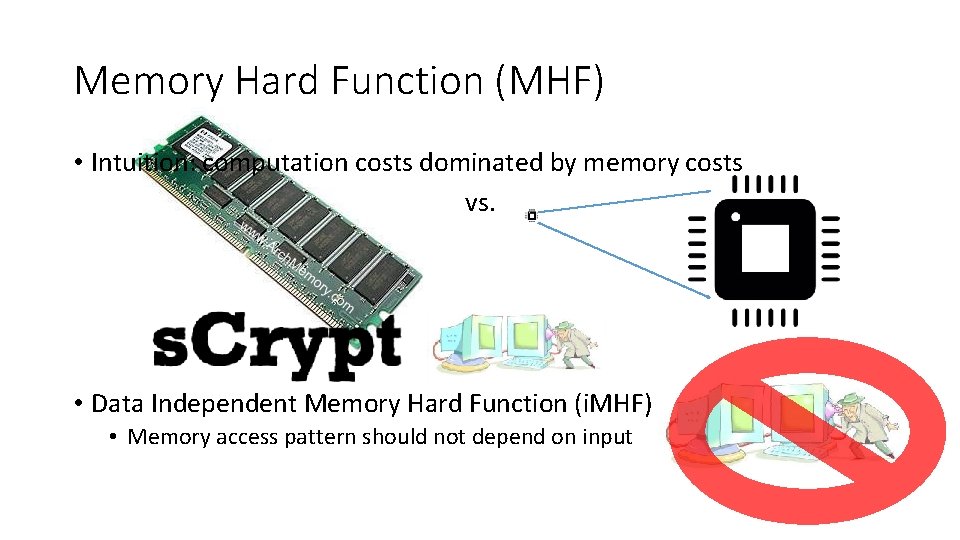
Memory Hard Function (MHF) • Intuition: computation costs dominated by memory costs vs. • Data Independent Memory Hard Function (i. MHF) • Memory access pattern should not depend on input

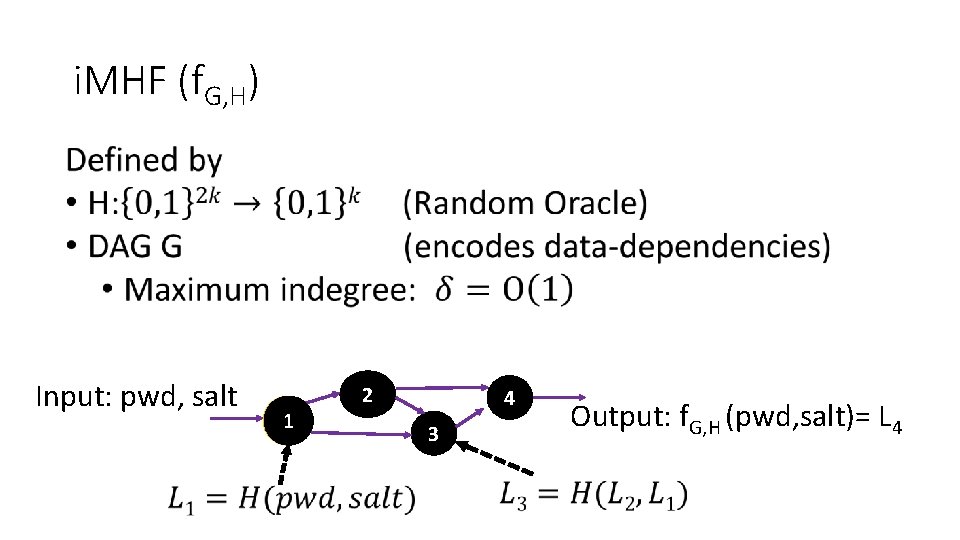
i. MHF (f. G, H) Input: pwd, salt 1 2 4 3 Output: f. G, H (pwd, salt)= L 4

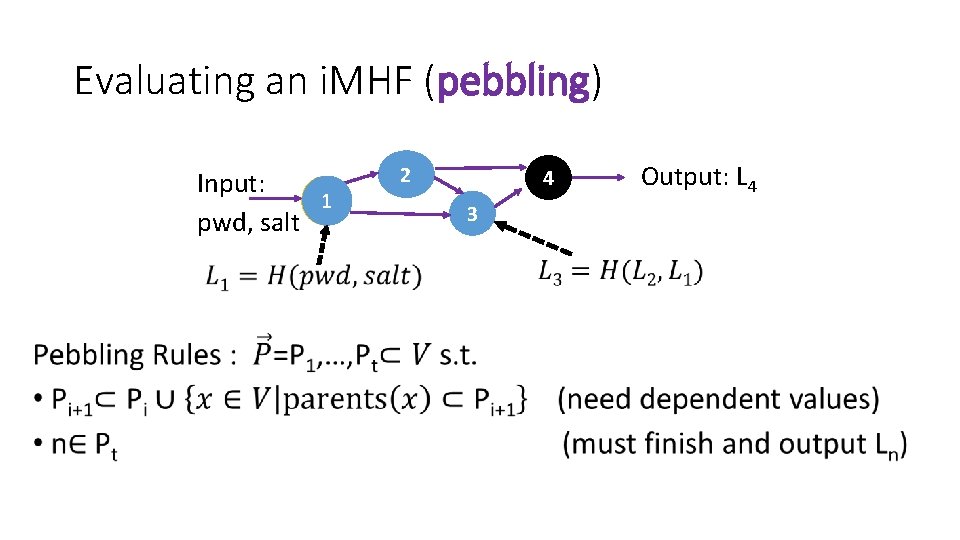
Evaluating an i. MHF (pebbling) Input: 1 pwd, salt • 2 4 3 Output: L 4

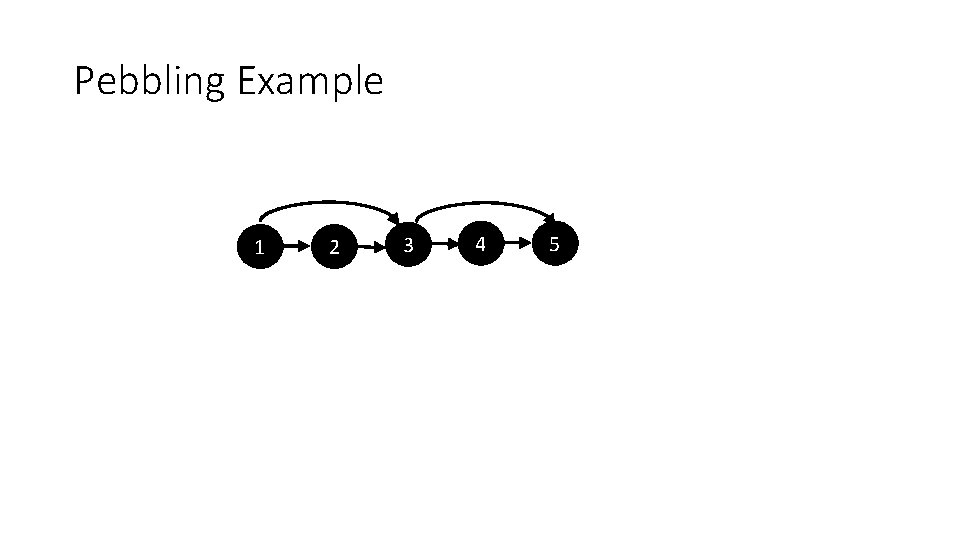
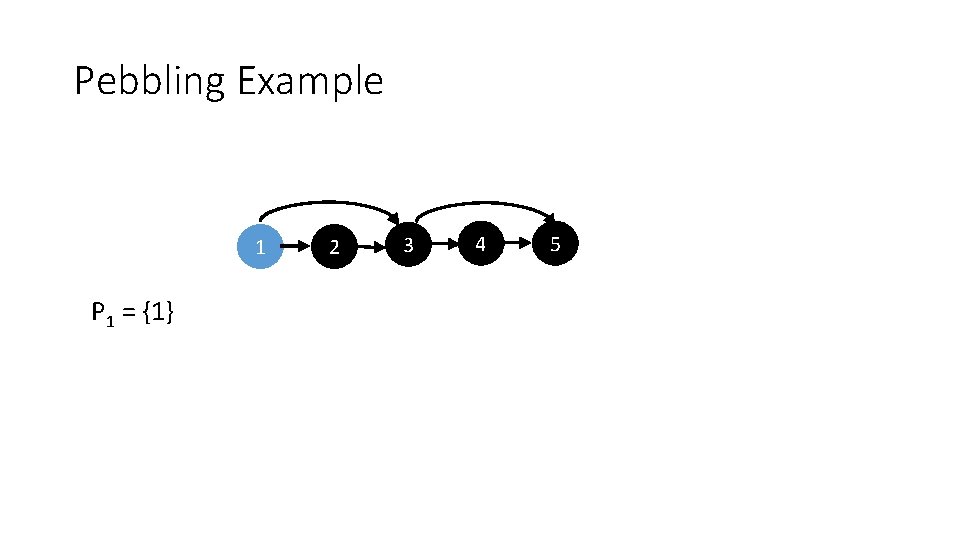
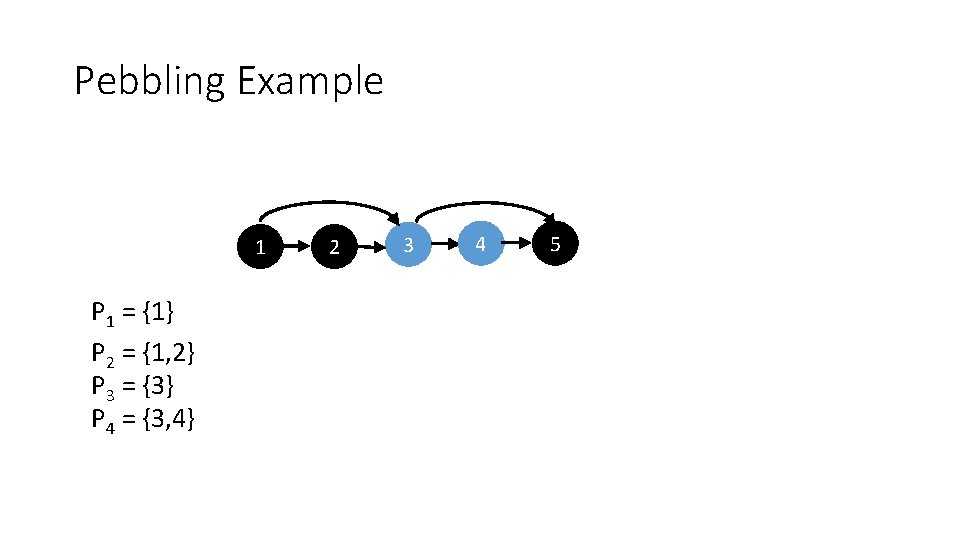
Pebbling Example 1 2 3 4 5

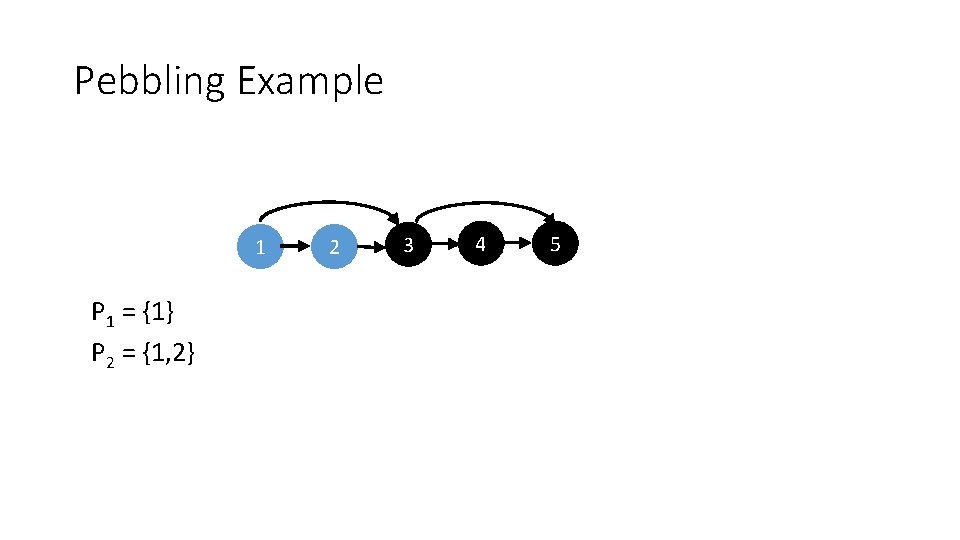
Pebbling Example 1 P 1 = {1} 2 3 4 5

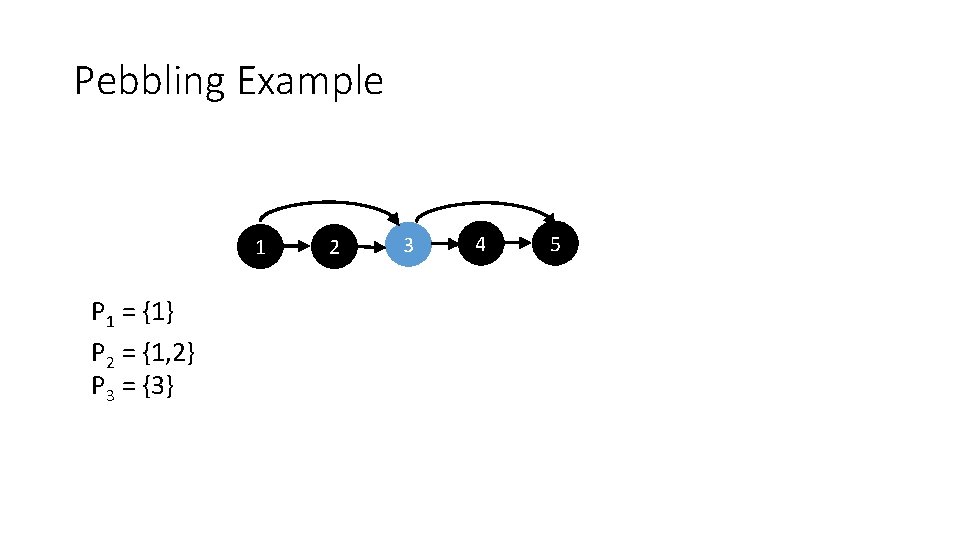
Pebbling Example 1 P 1 = {1} P 2 = {1, 2} 2 3 4 5

Pebbling Example 1 P 1 = {1} P 2 = {1, 2} P 3 = {3} 2 3 4 5

Pebbling Example 1 P 1 = {1} P 2 = {1, 2} P 3 = {3} P 4 = {3, 4} 2 3 4 5

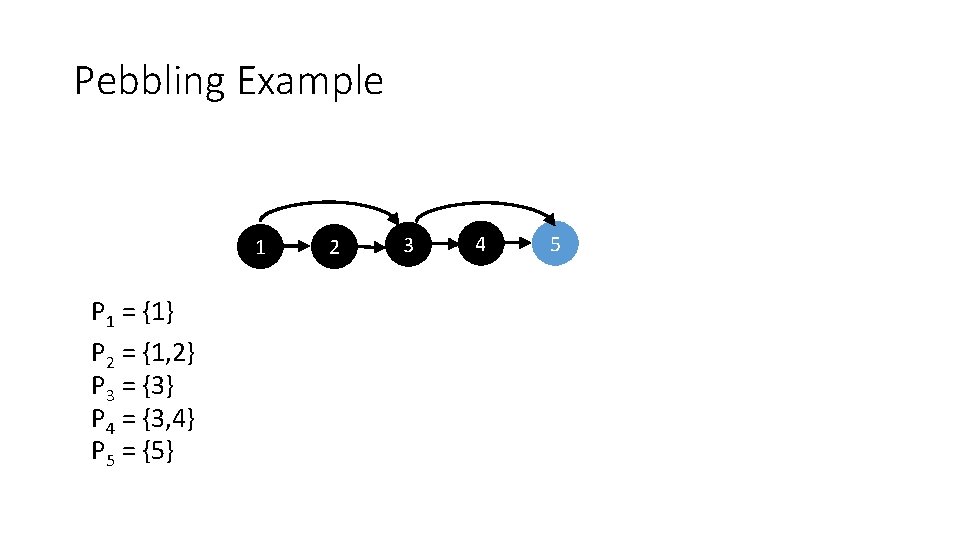
Pebbling Example 1 P 1 = {1} P 2 = {1, 2} P 3 = {3} P 4 = {3, 4} P 5 = {5} 2 3 4 5

Measuring Cost: Attempt 1 •

Amortization and Parallelism space • S 3 S 1 ST 1 = S 1 × T 1 ≈ S 3 × T 3 = ST 3 time T 1 T 3 cost of computing f once cost of computing f three times

Measuring Cost: Attempt 2 •

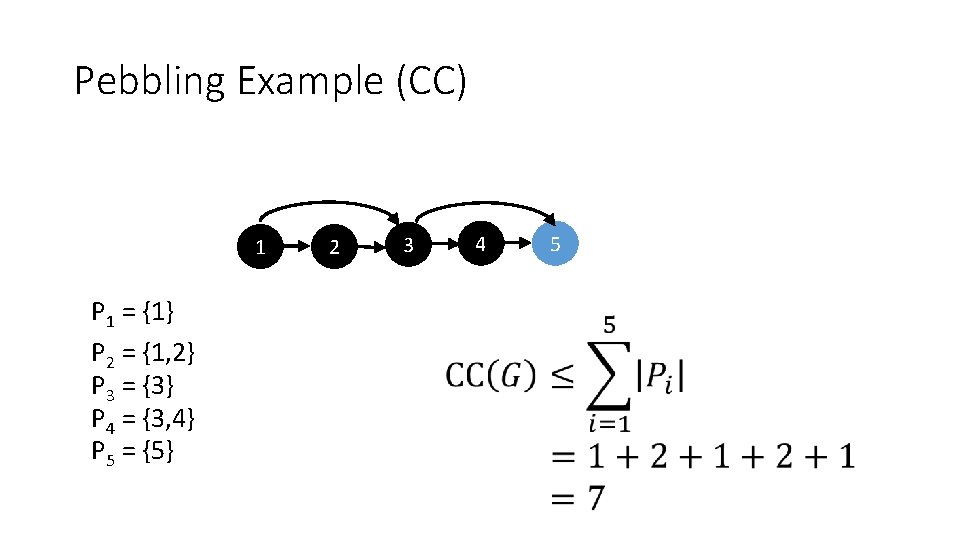
Pebbling Example (CC) 1 P 1 = {1} P 2 = {1, 2} P 3 = {3} P 4 = {3, 4} P 5 = {5} 2 3 4 5

Pebbling Equivalence

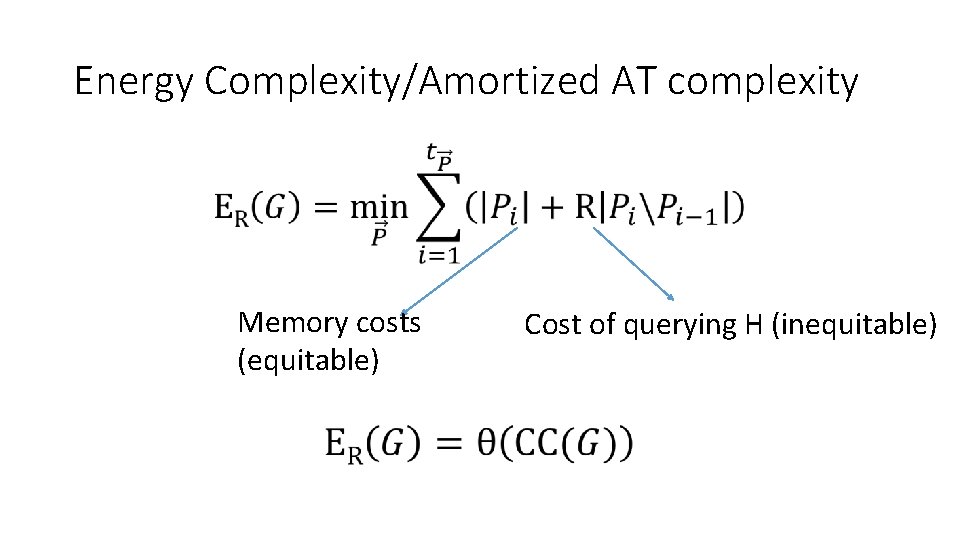
Energy Complexity/Amortized AT complexity • Memory costs (equitable) Cost of querying H (inequitable)

Naïve Pebbling Algorithms •

Amortized Attack Quality •

Desiderata • Memory costs should dominate

Desiderata • Maximize costs for fixed n (Users are impatient)

c-Ideal i. MHF •

Outline • Motivation • Data Independent Memory Hard Functions (i. MHFs) • Our Attacks • General Attack on Non Depth Robust DAGs • Existing i. MHFs are not Depth Robust • Ideal i. MHFs don’t exist • Subsequent Results (Depth-Robustness is Sufficient) • Open Questions

Depth-Robustness: The Key Property Necessary [AB 16] and sufficient [ABP 16] for secure i. MHFs

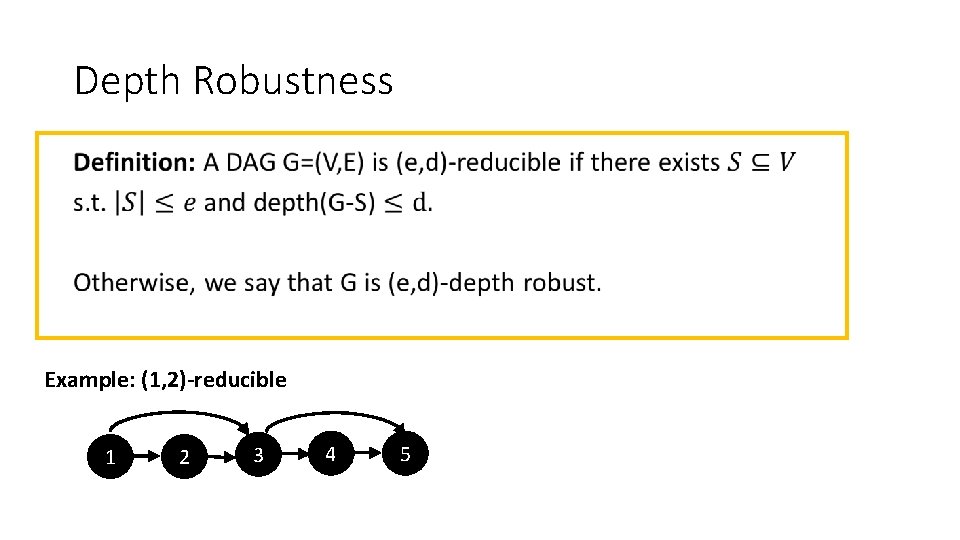
Depth Robustness • Example: (1, 2)-reducible 1 2 3 4 5

Depth Robustness • Example: (1, 2)-reducible 1 2 3 4 5

Attacking (e, d)-reducible DAGs •

Depth Robustness is Necessary •

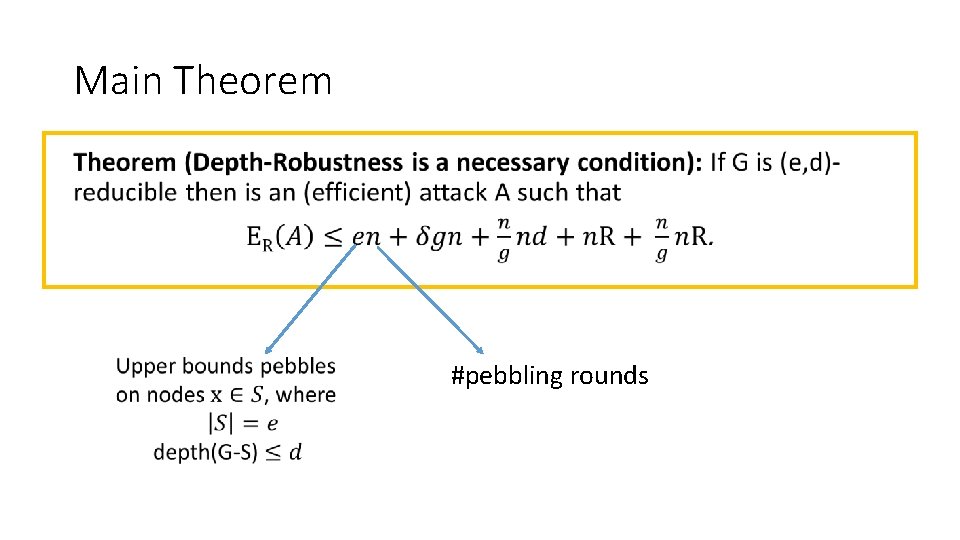
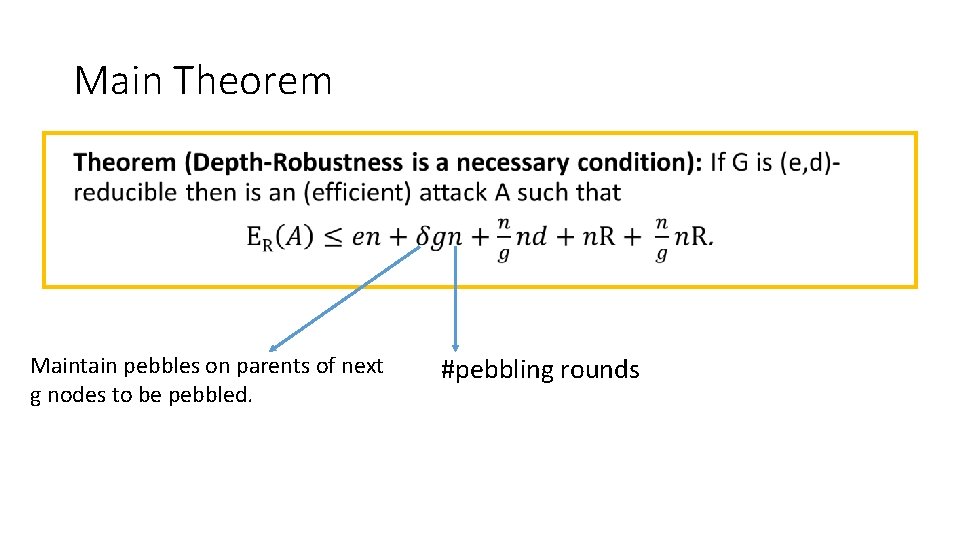
Main Theorem • #pebbling rounds

Main Theorem • Maintain pebbles on parents of next g nodes to be pebbled. #pebbling rounds

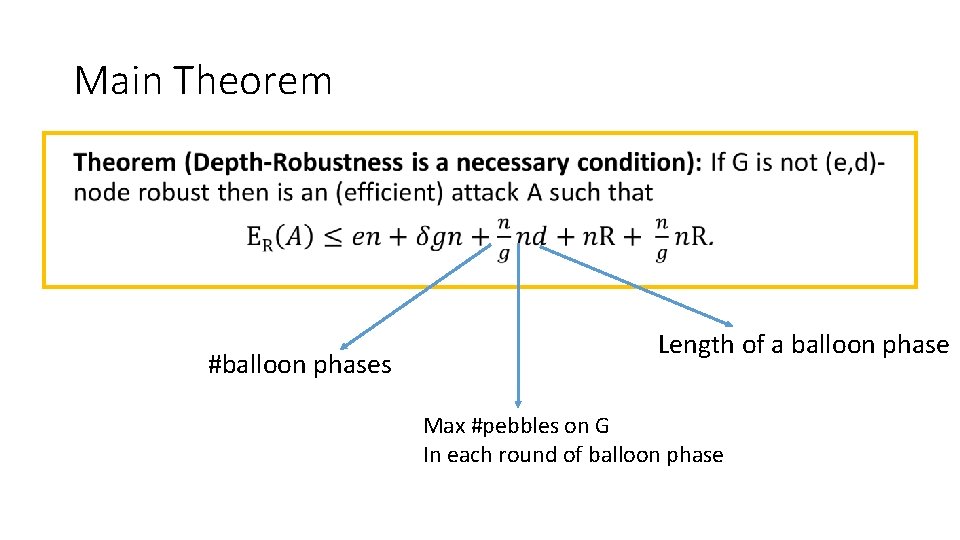
Main Theorem • #balloon phases Length of a balloon phase Max #pebbles on G In each round of balloon phase

Depth Robustness is Necessary •

Question Are existing i. MHF candidates based on depthrobust DAGs?

i. MHF Candidates • Catena [FLW 15] • Special Recognition at Password Hashing Competition • Two Variants: Dragonfly and Double-Butterfly • Argon 2 [BDK 15] • Winner of the Password Hashing Competition • Argon 2 i (data-independent mode) is recommended for Password Hashing • Balloon Hashing [BCS 16] • Newer proposal (three variants in original proposal)

Answer: No •

Argon 2 i [BDK] • Argon 2: Winner of the password hashing competition[2015] • Authors recommend Argon 2 i variant (data-independent) for password hashing.

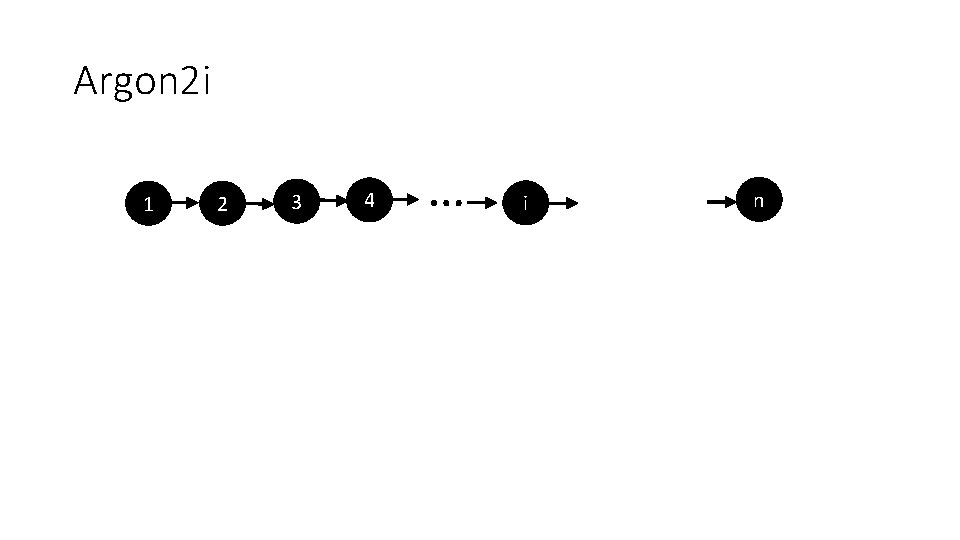
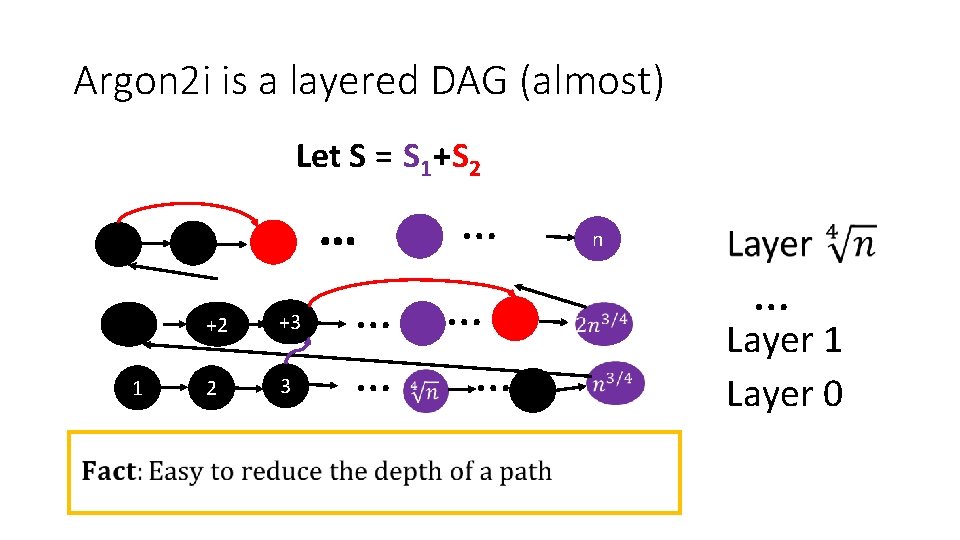
Argon 2 i 1 2 3 4 … i n

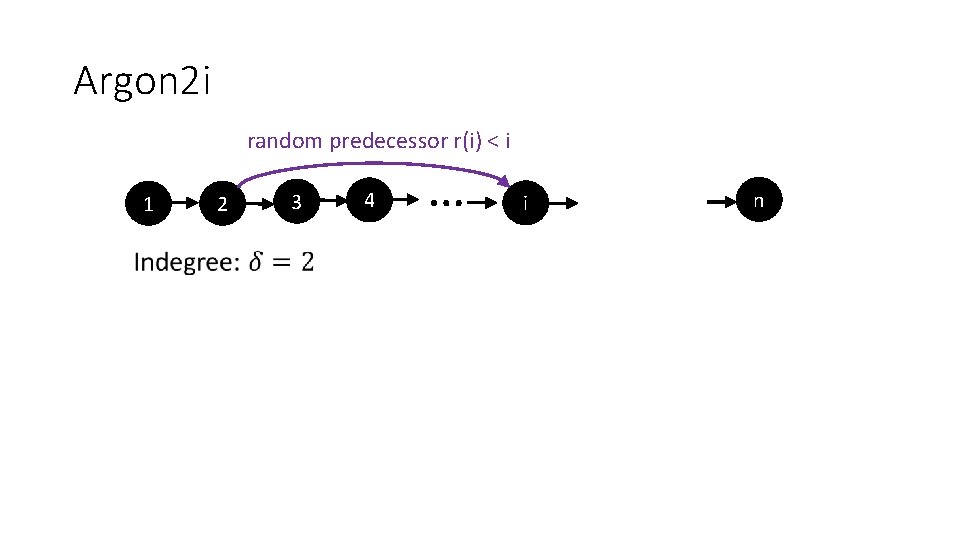
Argon 2 i random predecessor r(i) < i 1 2 3 4 … i n

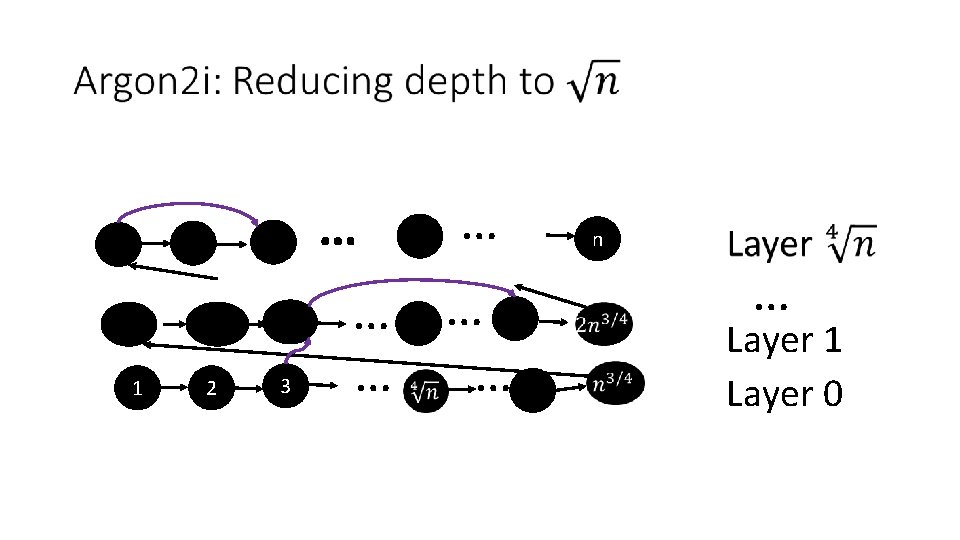
1 2 3 … … … n … Layer 1 Layer 0

1 2 3 … … … n … Layer 1 Layer 0

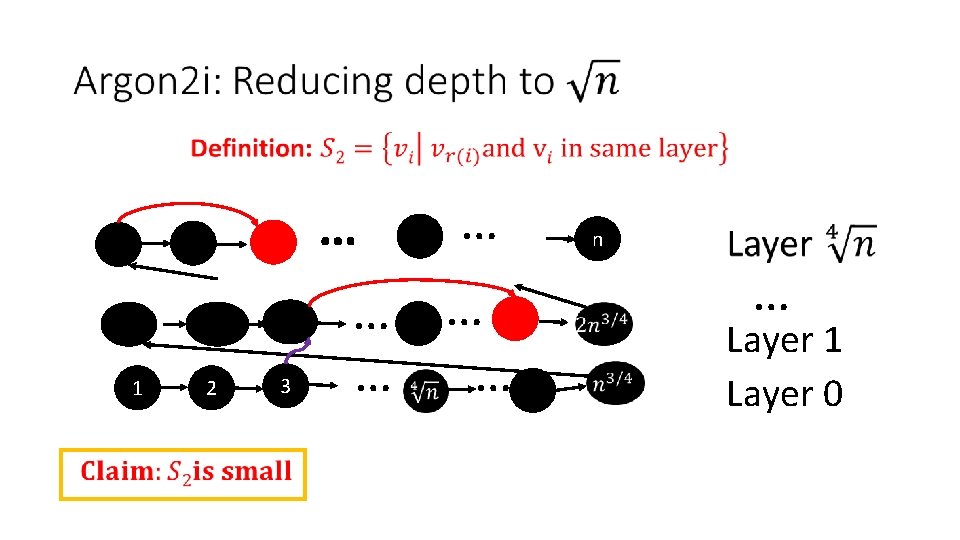
Argon 2 i is a layered DAG (almost) Let S = S 1+S 2 1 +2 +3 2 3 … … … n … Layer 1 Layer 0

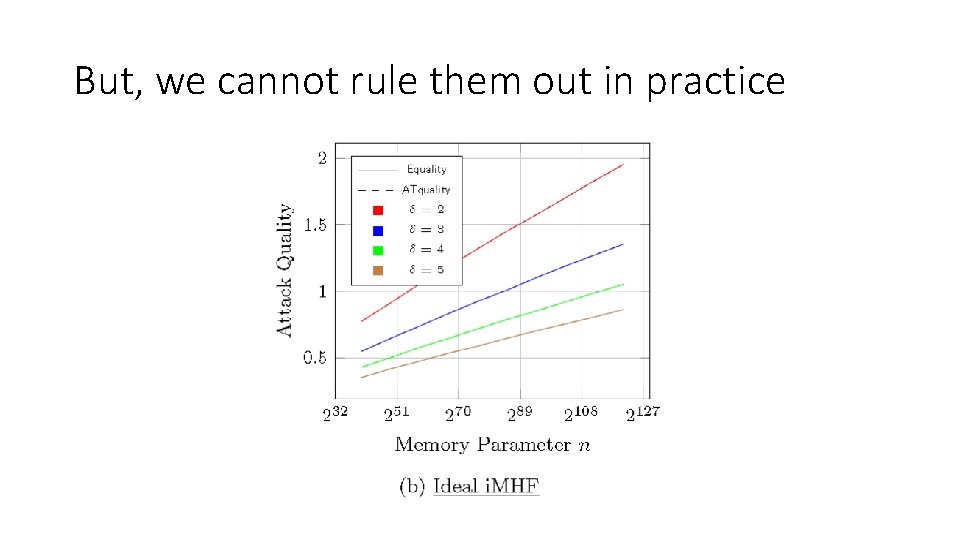
… Attack Simulation [AB 16 b] Parameter setting could easily be chosen when following Argon 2 i-B guidelines Pessimistic Argon 2 i-B parameter Attack on Argon 2 i-B is practical even for pessimistic parameter ranges (brown line).

Ideal i. MHFs Don’t Exist •

But, we cannot rule them out in practice

Outline • Motivation • Data Independent Memory Hard Functions (i. MHFs) • Attacks • Constructing i. MHFs (New!) • Depth-Robustness is sufficient • Conclusions and Open Questions

Depth-Robustness is Sufficient! [ABP 16]

Depth-Robustness is Sufficient! [ABP 16]

More New Results MHF Balloon Hash Argon 2 i (latest) Catena SCRYPT (data dependent) Upper Bound O(n 2) [Naïve, P 12] Lower Bound

Conclusions • Depth-robustness is a necessary and sufficient for secure i. MHFs • [AB 16] [ABP 16] • Big Challenge: Improved Constructions of Depth-Robust Graphs • We already have constructions in theory [EGS 77, PR 80, …] • But constants matter!

More Open Questions • Large Gap Remains

Thanks for Listening