TORQUE Y ROTACION Al aplicar una fuerza a

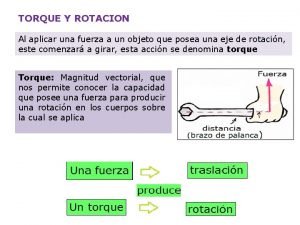
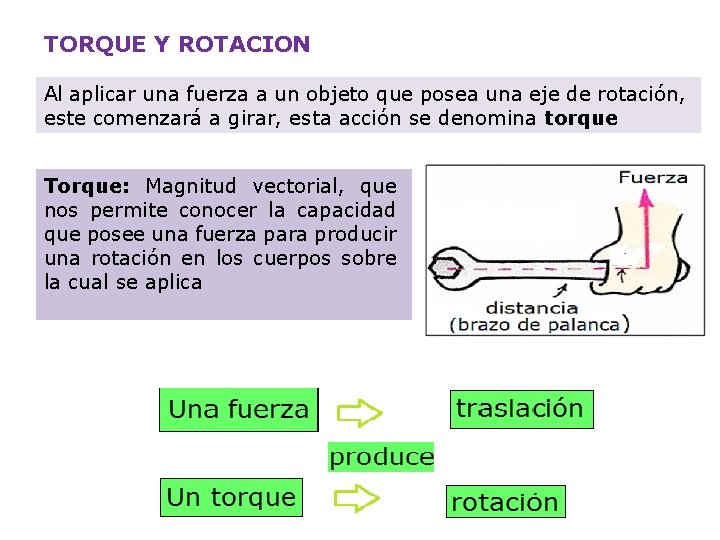
TORQUE Y ROTACION Al aplicar una fuerza a un objeto que posea una eje de rotación, este comenzará a girar, esta acción se denomina torque Torque: Magnitud vectorial, que nos permite conocer la capacidad que posee una fuerza para producir una rotación en los cuerpos sobre la cual se aplica

MAGNITUD DEL TORQUE • F=Fuerza aplicada [N] • d= distancia [m] • τ= Torque [Nm]

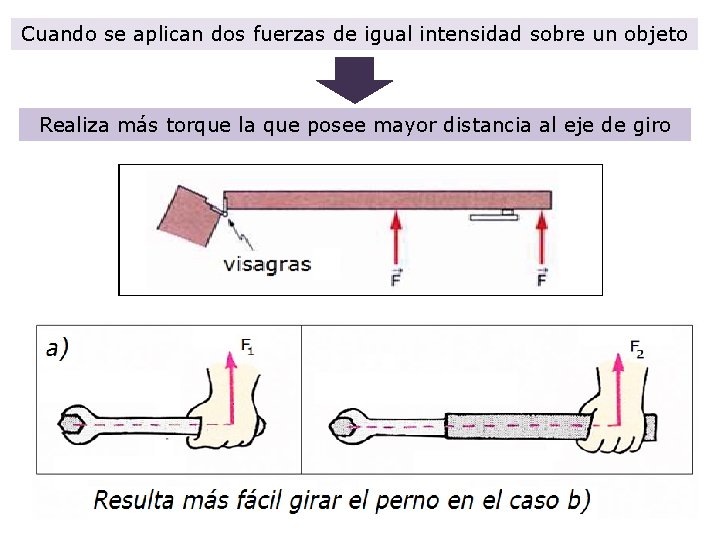
Cuando se aplican dos fuerzas de igual intensidad sobre un objeto Realiza más torque la que posee mayor distancia al eje de giro

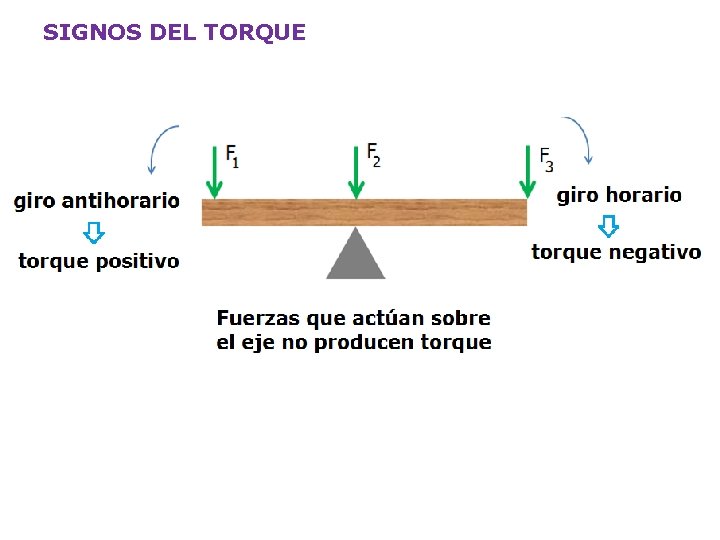
SIGNOS DEL TORQUE

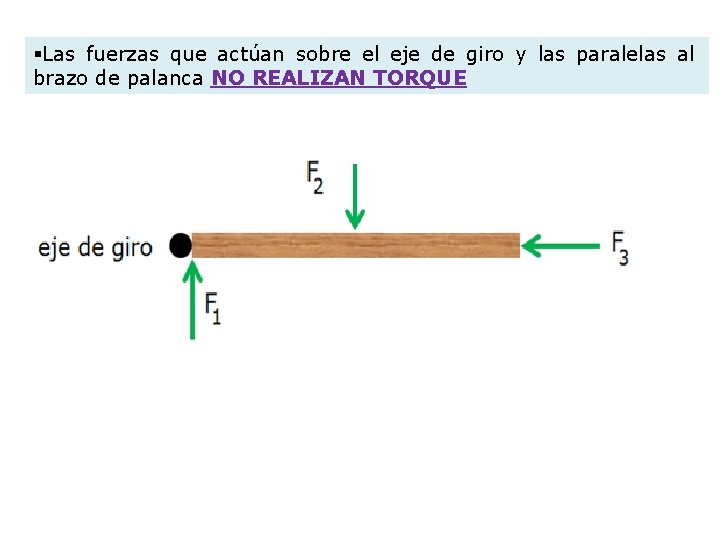
§Las fuerzas que actúan sobre el eje de giro y las paralelas al brazo de palanca NO REALIZAN TORQUE

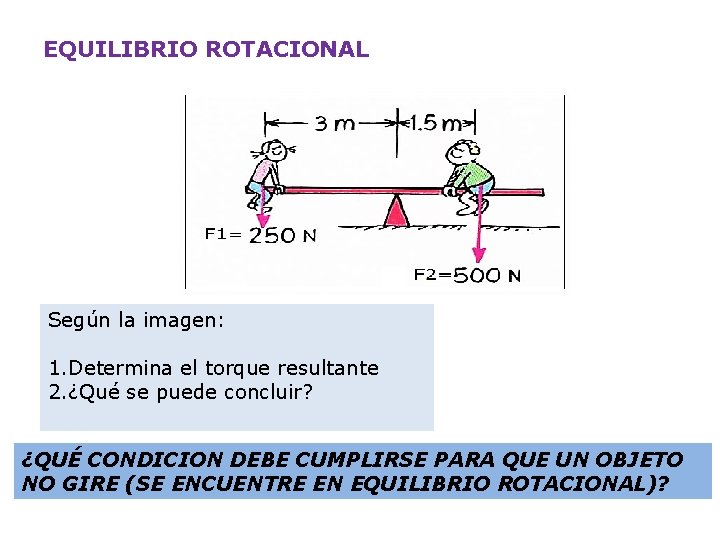
EQUILIBRIO ROTACIONAL Según la imagen: 1. Determina el torque resultante 2. ¿Qué se puede concluir? ¿QUÉ CONDICION DEBE CUMPLIRSE PARA QUE UN OBJETO NO GIRE (SE ENCUENTRE EN EQUILIBRIO ROTACIONAL)?

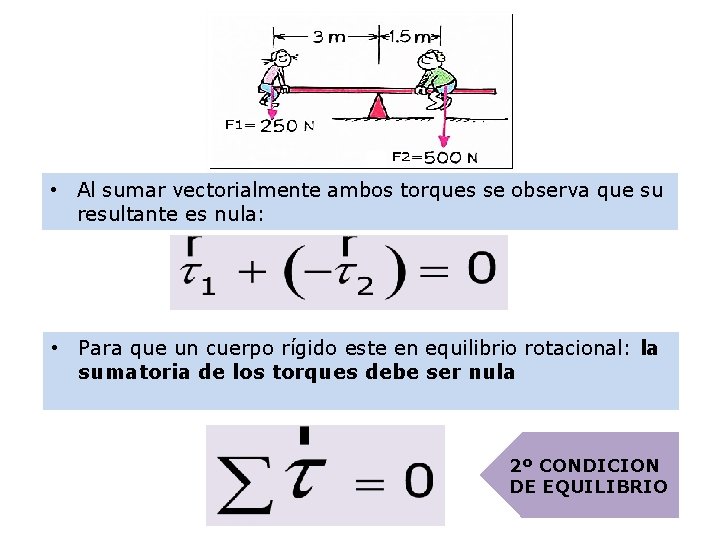
• Al sumar vectorialmente ambos torques se observa que su resultante es nula: • Para que un cuerpo rígido este en equilibrio rotacional: la sumatoria de los torques debe ser nula 2º CONDICION DE EQUILIBRIO

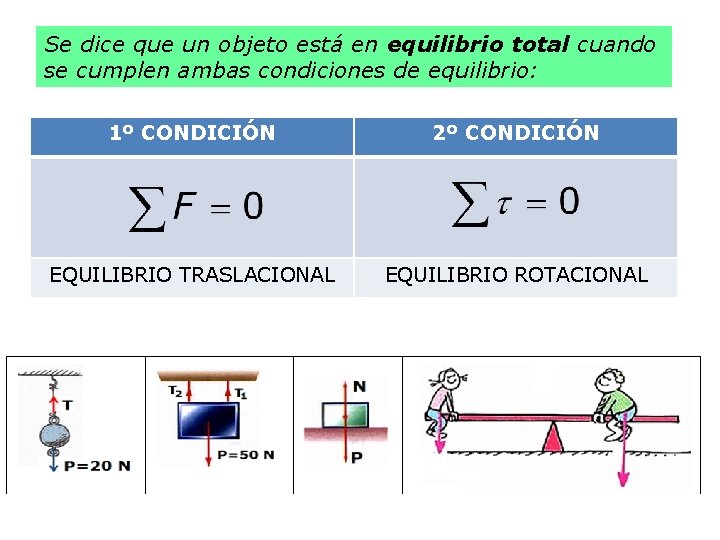
Se dice que un objeto está en equilibrio total cuando se cumplen ambas condiciones de equilibrio: 1º CONDICIÓN 2º CONDICIÓN EQUILIBRIO TRASLACIONAL EQUILIBRIO ROTACIONAL

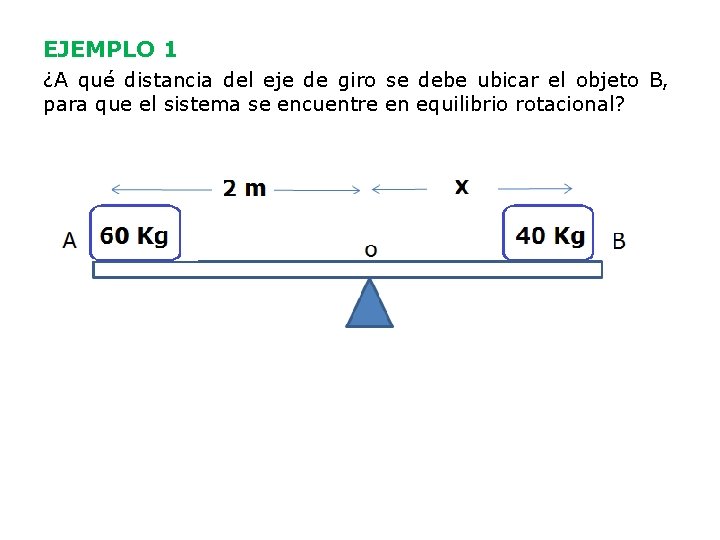
EJEMPLO 1 ¿A qué distancia del eje de giro se debe ubicar el objeto B, para que el sistema se encuentre en equilibrio rotacional?

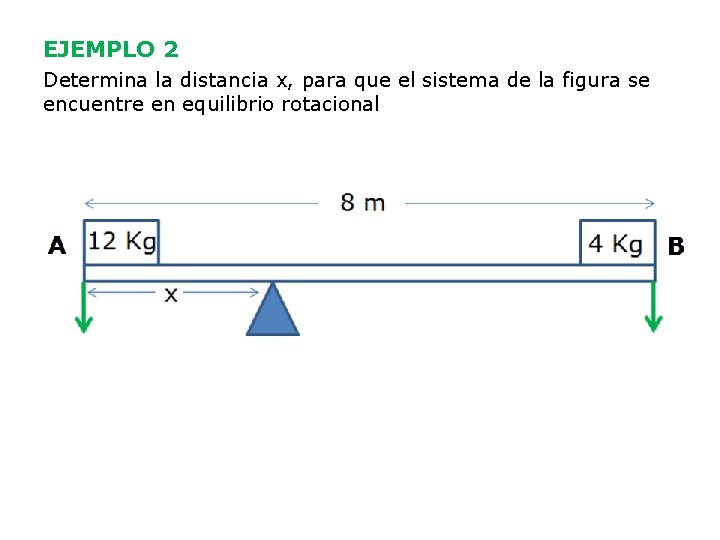
EJEMPLO 2 Determina la distancia x, para que el sistema de la figura se encuentre en equilibrio rotacional

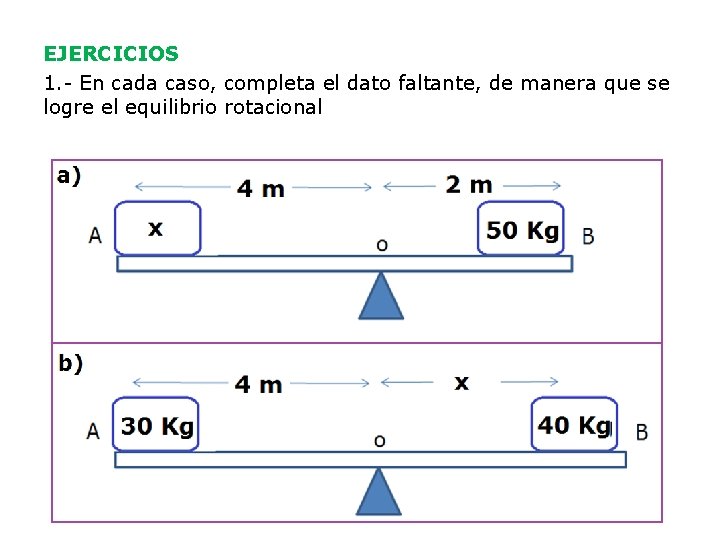
EJERCICIOS 1. - En cada caso, completa el dato faltante, de manera que se logre el equilibrio rotacional

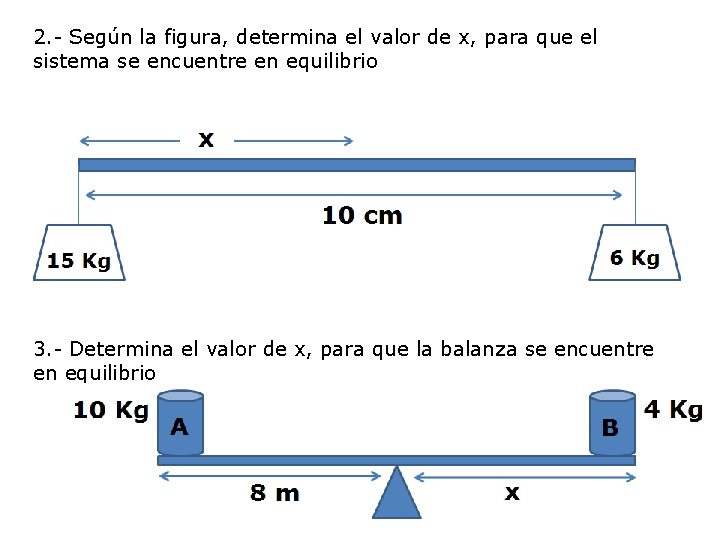
2. - Según la figura, determina el valor de x, para que el sistema se encuentre en equilibrio 3. - Determina el valor de x, para que la balanza se encuentre en equilibrio

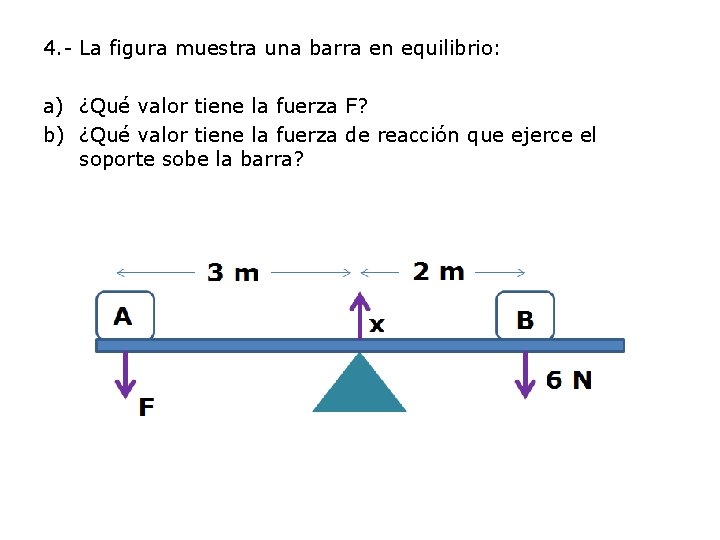
4. - La figura muestra una barra en equilibrio: a) ¿Qué valor tiene la fuerza F? b) ¿Qué valor tiene la fuerza de reacción que ejerce el soporte sobe la barra?

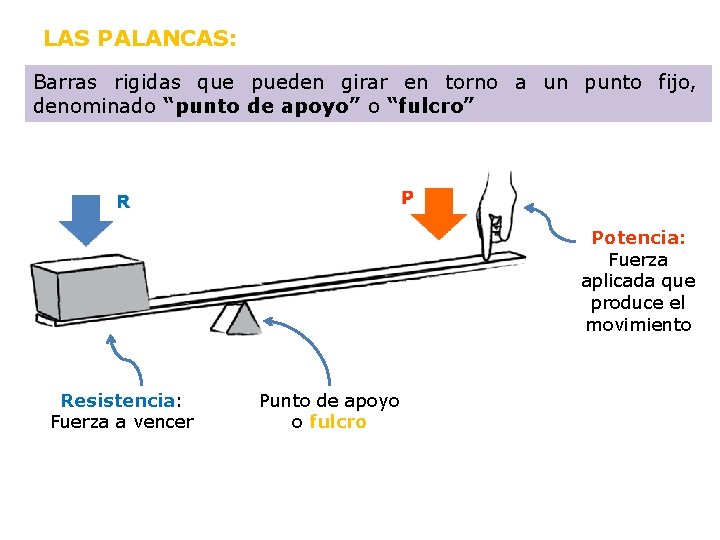
LAS PALANCAS: Barras rigidas que pueden girar en torno a un punto fijo, denominado “punto de apoyo” o “fulcro” Potencia: Fuerza aplicada que produce el movimiento Resistencia: Fuerza a vencer Punto de apoyo o fulcro

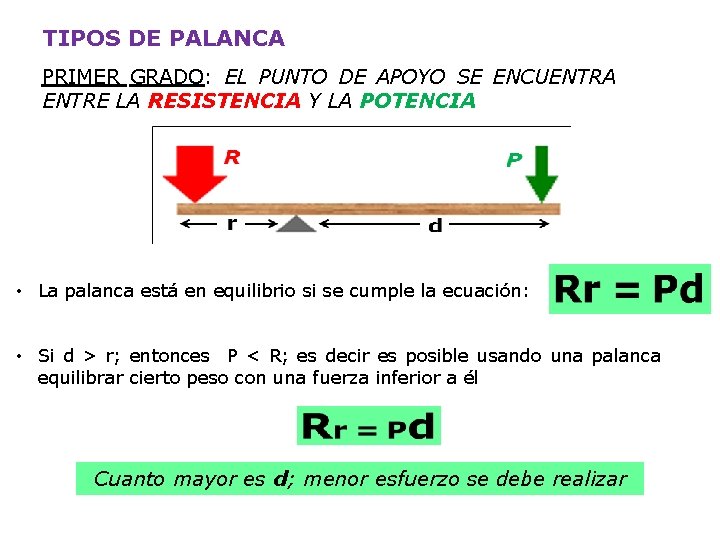
TIPOS DE PALANCA PRIMER GRADO: EL PUNTO DE APOYO SE ENCUENTRA ENTRE LA RESISTENCIA Y LA POTENCIA • La palanca está en equilibrio si se cumple la ecuación: • Si d > r; entonces P < R; es decir es posible usando una palanca equilibrar cierto peso con una fuerza inferior a él Cuanto mayor es d; menor esfuerzo se debe realizar

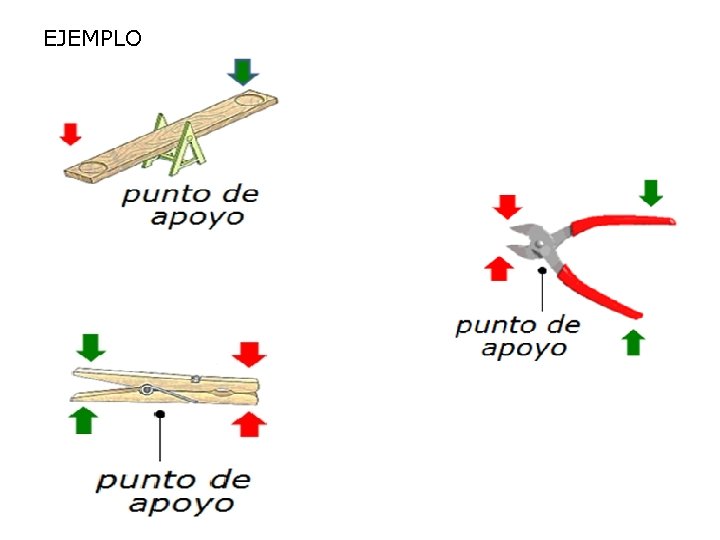
EJEMPLO

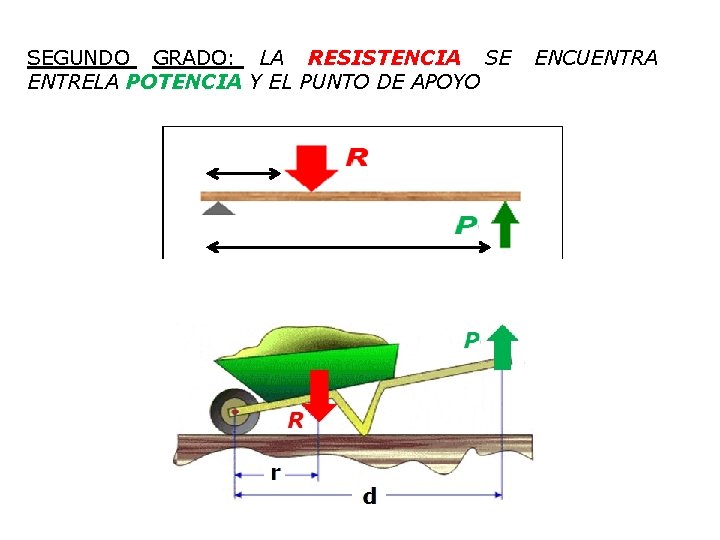
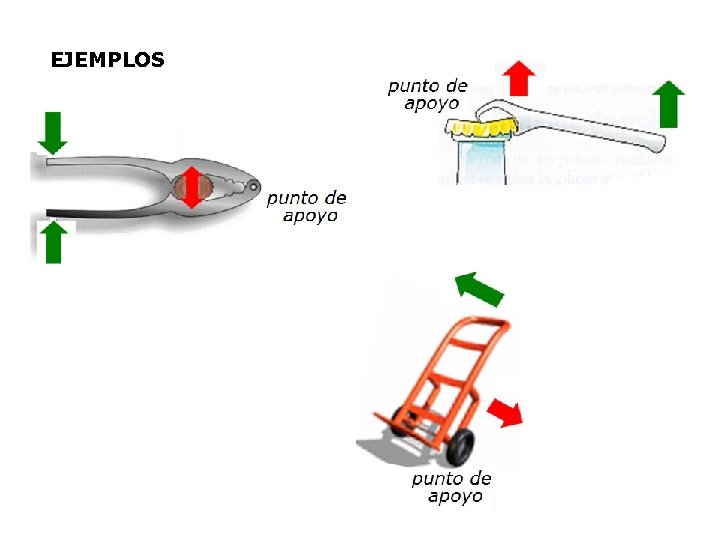
SEGUNDO GRADO: LA RESISTENCIA SE ENTRELA POTENCIA Y EL PUNTO DE APOYO ENCUENTRA

EJEMPLOS

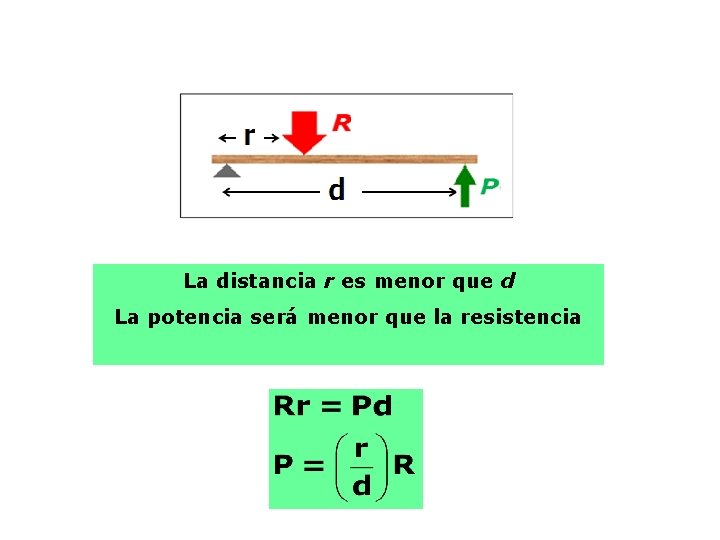
La distancia r es menor que d La potencia será menor que la resistencia

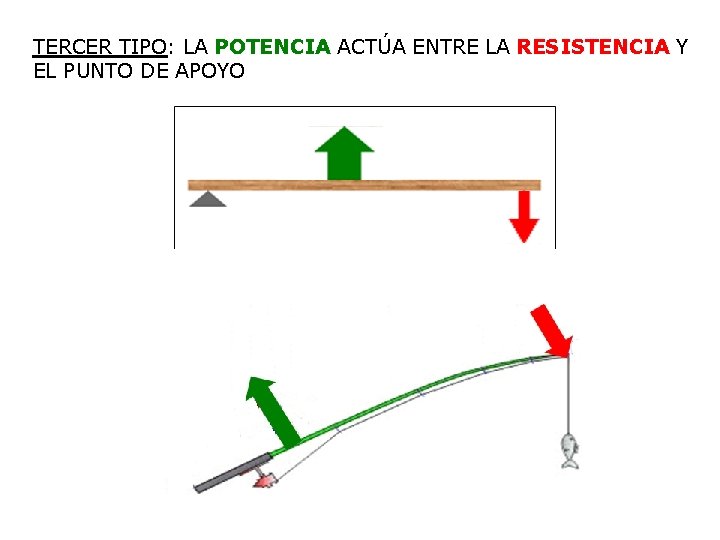
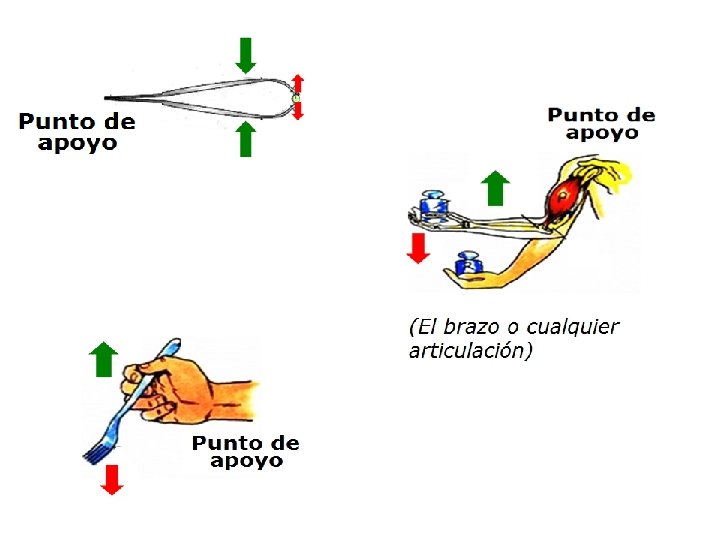
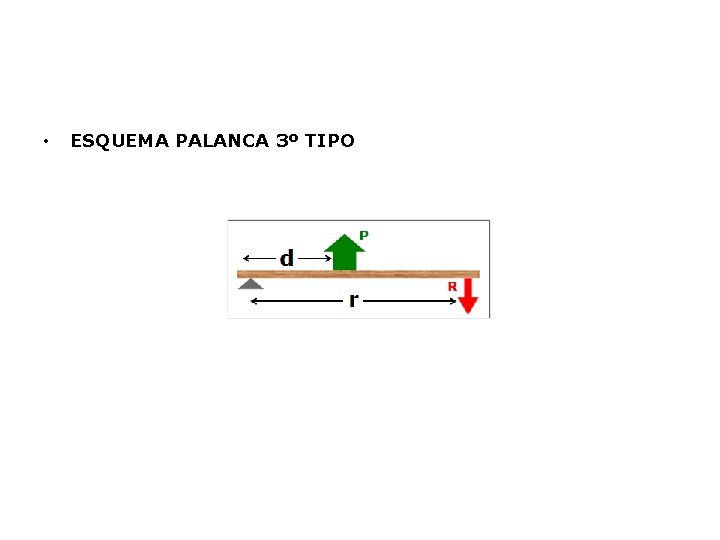
TERCER TIPO: LA POTENCIA ACTÚA ENTRE LA RESISTENCIA Y EL PUNTO DE APOYO

• ESQUEMA PALANCA 3º TIPO