Torque Centre of mass balancing a clamp stand

Torque

Centre of mass: balancing a clamp stand sideways The point on an object where all its weight is balanced on either side is called the centre of gravity or the centre of mass.

Centre of mass You can treat the force of gravity like it always acts through the centre of mass

contact force of pivot (reaction force) weight of stand If you support an object through its centre of mass, the object will be in equilibrium

contact force of pivot (reaction force) weight of stand The equal and opposite forces are acting on the same point, so the object is in equilibrium.

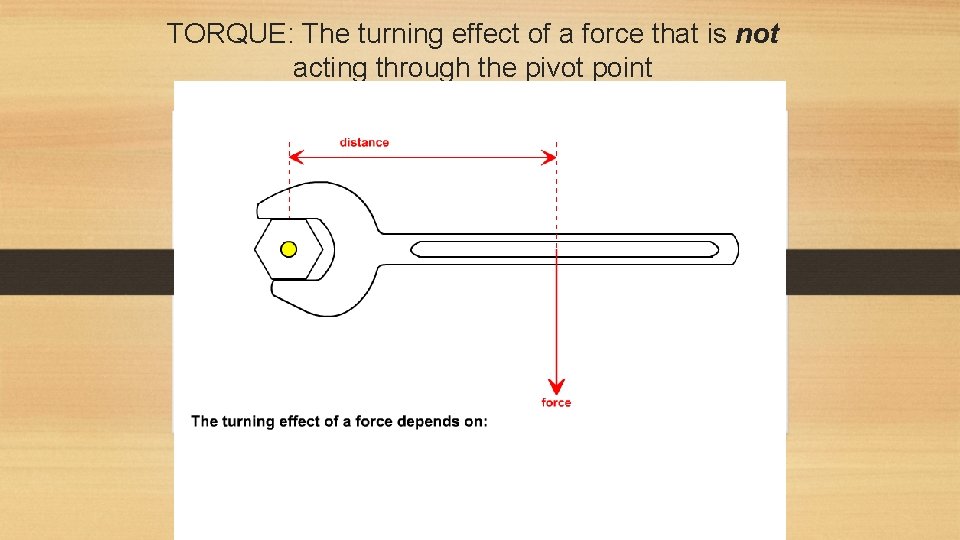
TORQUE: The turning effect of a force that is not acting through the pivot point

Is it easier to push a door open near the hinges or away from the hinges?

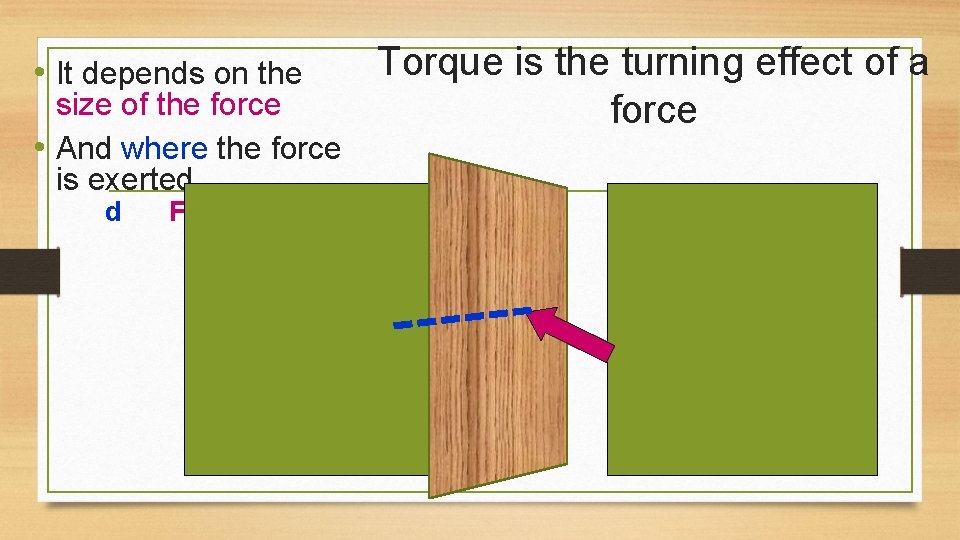
• It depends on the size of the force • And where the force is exerted d F Torque is the turning effect of a force

• The turning effect of a force is …… • d is the distance from the force to the pivot • The units for torque are …………

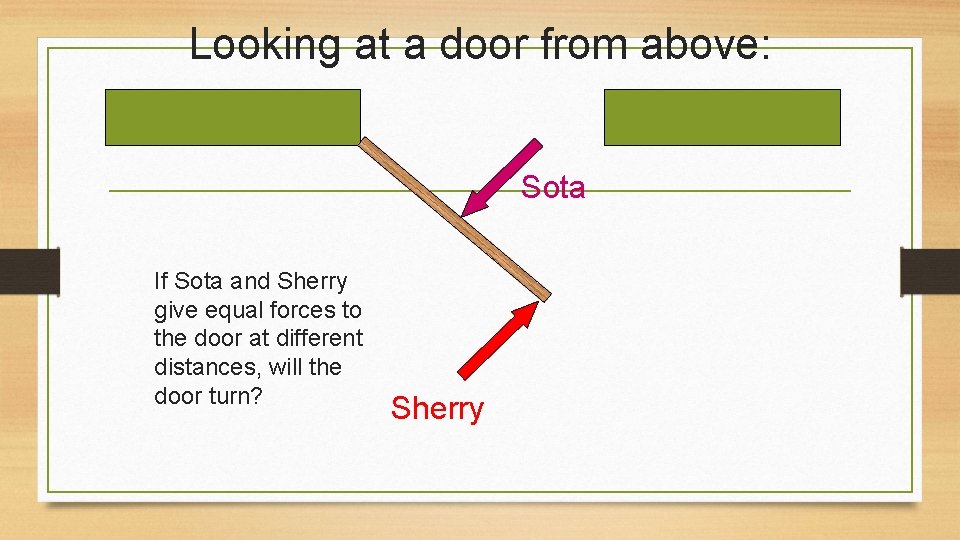
Looking at a door from above: Sota If Sota and Sherry give equal forces to the door at different distances, will the door turn? Sherry

Conditions for Equilibrium An object is in equilibrium (or balanced) if: • The sum of all the forces acting on it is zero. This means that the net force is zero AND • The sum of the torques on it is zero. Net torque is zero. clockwise torques = anti clockwise torques

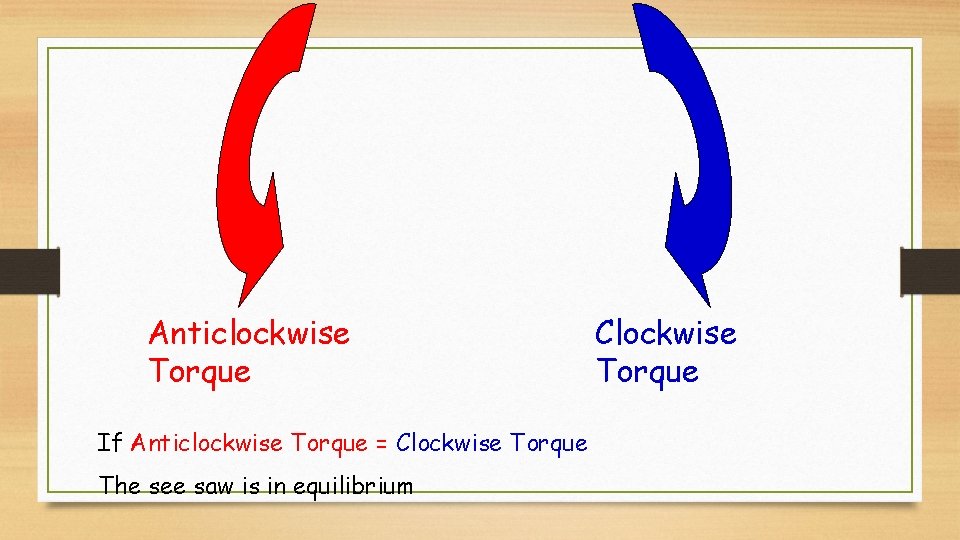
Anticlockwise Torque If Anticlockwise Torque = Clockwise Torque The see saw is in equilibrium Clockwise Torque

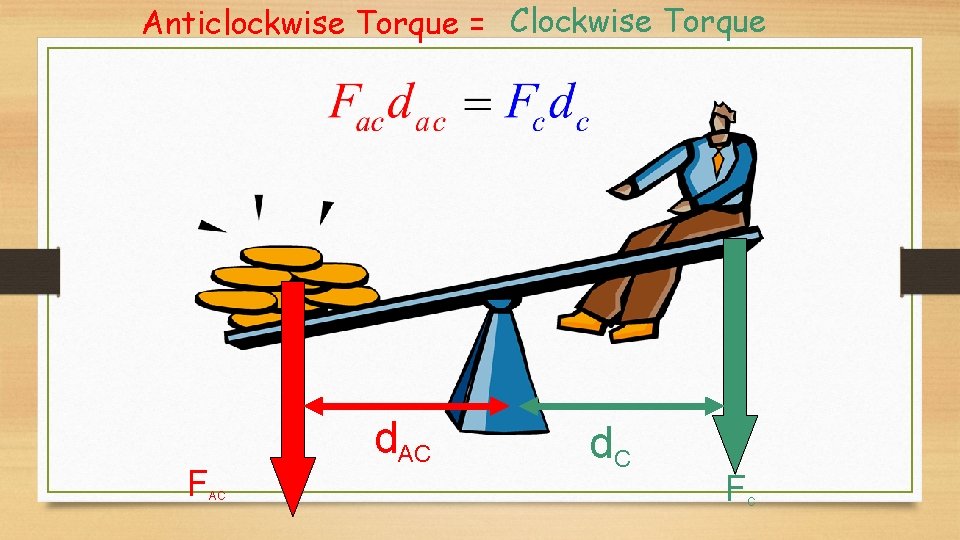
Anticlockwise Torque = Clockwise Torque F d. AC AC d. C F C

Torque calculation 1 In the following diagram below sufficient data is given to find the unknown force labelled F. Assume equilibrium exists and use the concept of clockwise torque equals anticlockwise torque. Also assume that the beam has negligible weight. .

Answer: clockwise torque = anticlockwise torque F x 2. 0 = 10 x 0. 8 F = 8/2 = 4 N

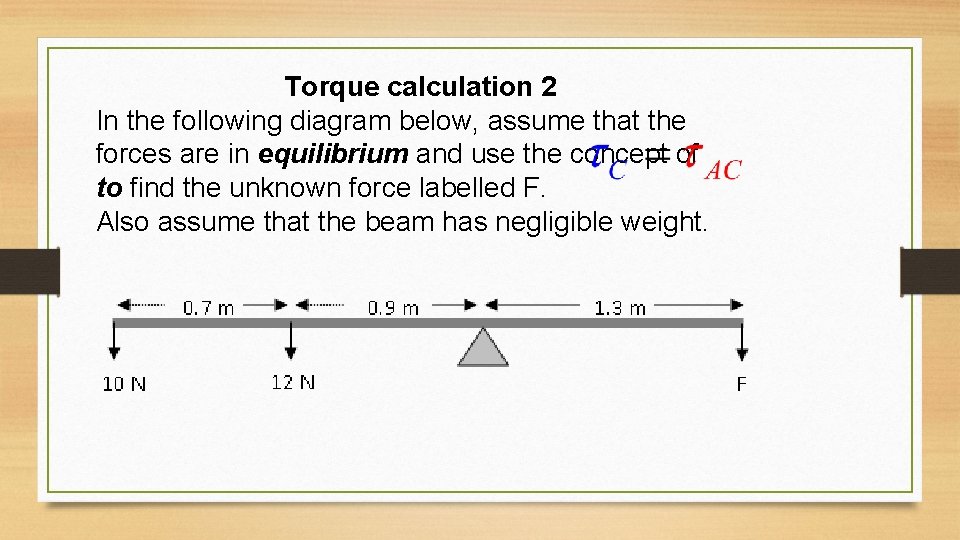
Torque calculation 2 In the following diagram below, assume that the forces are in equilibrium and use the concept of to find the unknown force labelled F. Also assume that the beam has negligible weight.

Answer to torque calculation 2 clockwise torque = anticlockwise torque F x 1. 3 = (12 x 0. 9) + (10 x 1. 6) F = (10. 8 + 16)/1. 3 = 20. 6 = 21 N

Answer to torque calculation 4 c

Hannah is 50 kg, the plank is 6 m, Leo is 1 m from the end. The pivot point is in the centre of the plank, which is balanced and not rotating. Calculate Leo’s mass.

Anticlockwise Torque = Clockwise Torque 50 x 9. 8 x 3 = m x 9. 8 x 2 150 = m x 2 150 / 2= m 75 kg = m

Solving Torque Problems: 1) Identify the pivot 2) Identify all the forces and their distances from the pivot 3) Decide if each force is causing clockwise or anticlockwise rotation 4) Set 5) Substitute if in equilibrium force x distance from the pivot for each force acting in the clockwise direction 6) Repeat the last step for the anti-clockwise torque 7) Solve for your unknown.

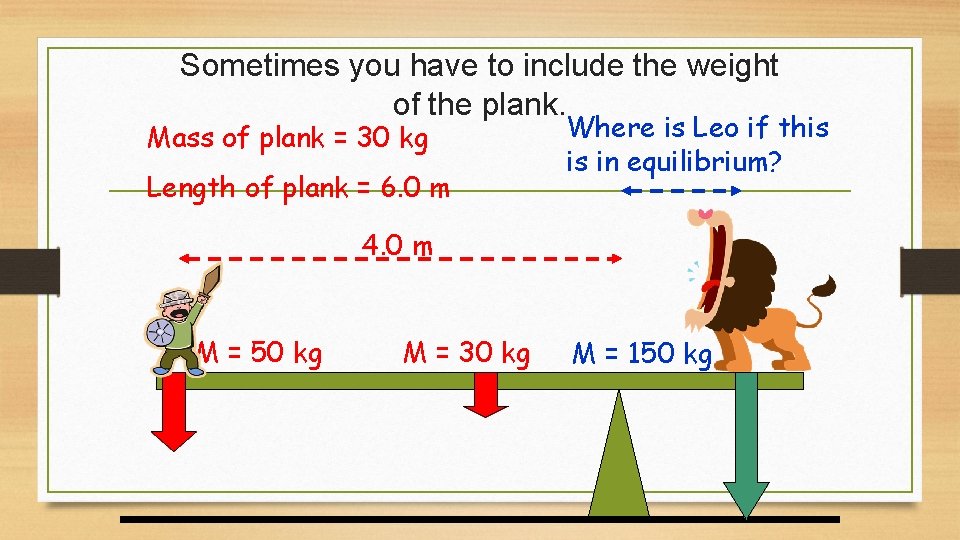
Sometimes you have to include the weight of the plank. Mass of plank = 30 kg Length of plank = 6. 0 m Where is Leo if this is in equilibrium? 4. 0 m M = 50 kg M = 30 kg M = 150 kg

Answer Hannah’s weight, FHannah is 4 m from pivot, Plank’s Weight, Fplank is 4 -3 = 1 m from pivot Leo’s Weight, Fleo is a distance, d from pivot clockwise torque = anticlockwise torque (50 x 9. 8 x 4 )+ ( 30 x 9. 8 x 1) = 150 x 9. 8 x d 1960 + 294 = 1470 d 2254= 1470 d 2254 / 1470 = d 1. 53 m = d

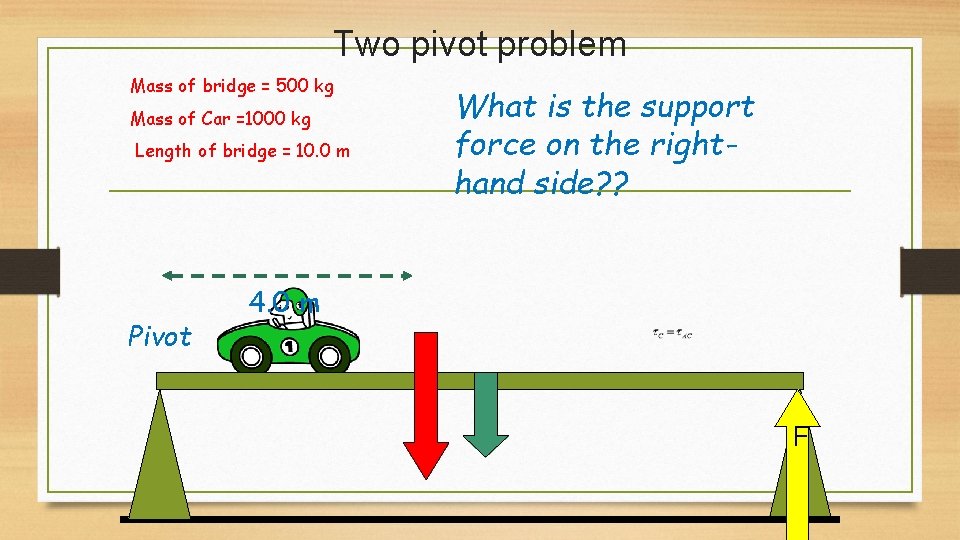
Two pivot problem Mass of bridge = 500 kg Mass of Car =1000 kg Length of bridge = 10. 0 m Pivot What is the support force on the righthand side? ? 4. 0 m F

answer • • • Clockwise = anticlockwise 500 x 9. 8 x 5 + 1000 x 9. 8 x 4 = F x 10 24500 + 39200 =10 F 63700 = 10 F 6370 N = F

Two-pivot problems: 1. Treat one of the supports as a pivot 2. Treat the other support as a force 3. Decide which forces are causing clockwise torques 4. Decide which forces are causing anti clockwise torques. 5. Continue solving as you would for a one-pivot problem

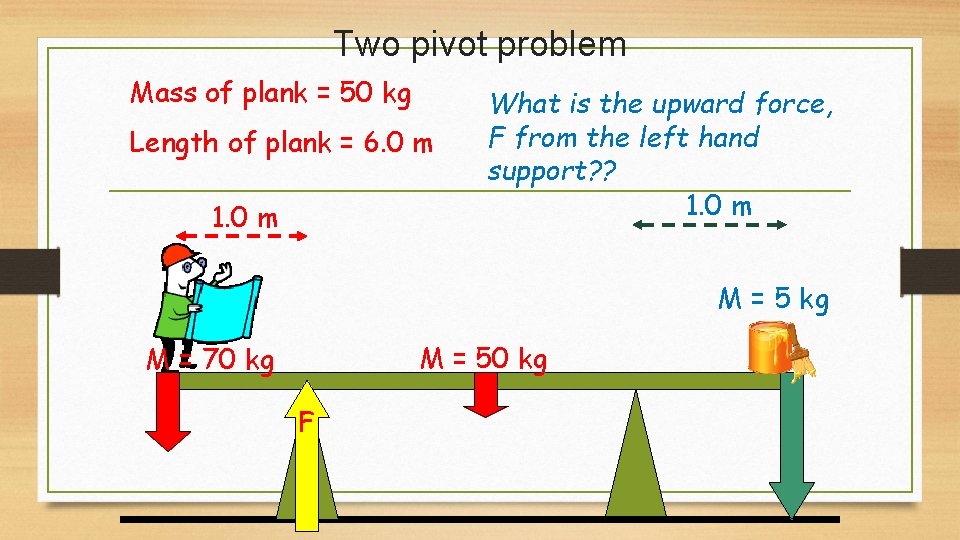
Two pivot problem Mass of plank = 50 kg Length of plank = 6. 0 m 1. 0 m What is the upward force, F from the left hand support? ? 1. 0 m M = 5 kg M = 50 kg M = 70 kg F

METHOD 1: Anticlockwise torque= clockwise torque 70 X 9. 8 x 5 + 50 x 9. 8 x 2 = 5 x 9. 8 x 1 + F x 4 3430 + 980 = 49 + 4 F 4361 = 4 F F = 1090. 25 N = 1090 N METHOD 2: Clockwise torque = anti clockwise torque (F x 4) + (5 x 9. 8 x 1) = (70 x 9. 8 x 4) + ( 50 x 9. 8 x 2) 4 F + 49 = 3430 + 980 4 F + 49 = 4410 4 F = 4410 – 49 = 4361 F = 4361/4 = 1090. 25 = 1090 N

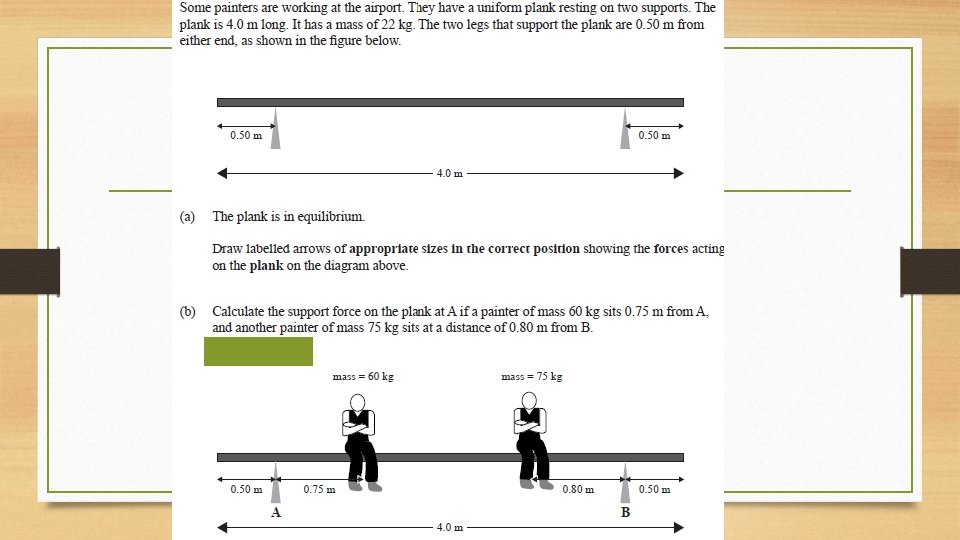
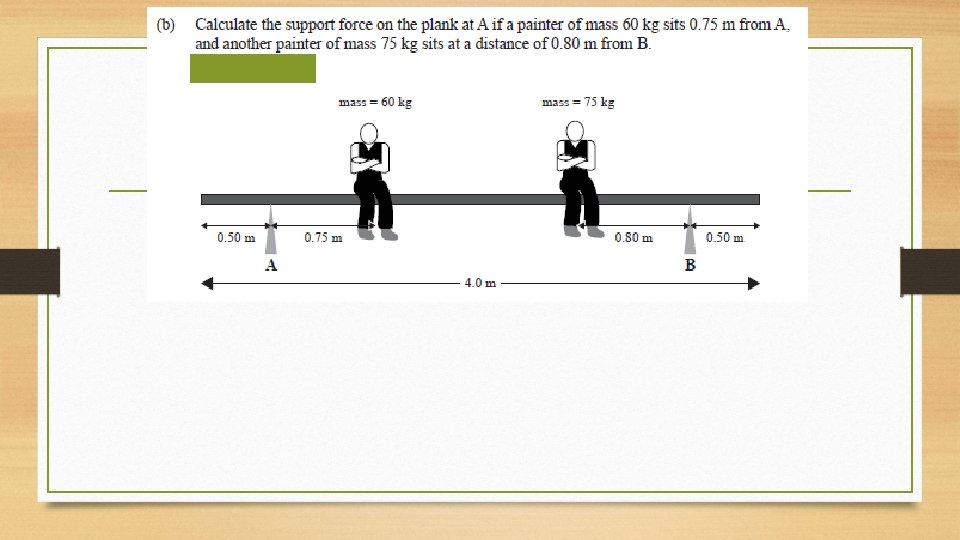
Answers to question 5 a) Using 1 tonne produces a gravity force of 10000 N (F = 1000 x g) Taking moments(torque) about F 2 and using moments Tc clockwise moments = Tac anticlockwise F 1 x 80 = (294000 (30000 x 9. 8) x 40 (40 m to F 2(the pivot)) + (49000 (5000 x 9. 8) x 60 (20 m+ 40 m to F 2 the pivot) F 1 = (11760000 + 2940000)/80 = 183750 N Fnet = 0 Therefore, the upwards forces of F 1 & F 2 balance the downwards force of gravity of the bridge and the truck. F 1= 183750 N F 1 + F 2 = 343000 Fg truck= 294000 N F 2 = 343000 - 183750 Fg bridge= 49000 N F 2 = 159 250 N, upwards

(b) Tc = Tac F 1 x 64 = ((4000 x 9. 8) (Fg truck)x 10 (d to pivot F 2)) + ((25000 x 9. 8) x 32 (d to pivot F 2)) F 1 = (392000 + 7840000)/64 ( from other side to get F 1 alone)= 128 625 N Fnet = 0 Therefore, the upwards forces of F 1 & F 2 balance the downwards force of gravity of the bridge and the truck. F 1= 128625 N F 1 + F 2 = 284200 Fg truck= 39200 N F 2 = 284200 - 128625 Fg bridge= 245000 N F 2 = 155 575 N, upwards

(c) F 1 x 48 = ((3000 x 9. 8)x 8(distance of truck 1 to F 2) + ((35000 x 9. 8)x 24(distance of bridge mass to F 2) + ((4000 x 9. 8) x 39(distance of truck 2 to F 2) F 1 = (235200+ 8232000+ 1528800)/48 (Divide to get F 1 alone) = 208 250 N Fnet = 0 Therefore, the upwards forces of F 1 & F 2 balance the downwards force of gravity of the bridge and the two trucks. F 1= 208 250 N F 1 + F 2 = 411 600 Fg truck 1= 29 400 N F 2 = 411 600 - 208 250 Fg bridge= 343000 N F 2 = 203 350 N, upwards Fg truck 2= 39 200 N