Torque AP Physics 1 Causing Rotational Motion In

Torque AP Physics 1

Causing Rotational Motion • In order to make an object start rotating about an axis, a torque is required. • Torque includes not only the amount of force applied but also the distance from the axis to which the force is applied. • Distance from axis is called the lever arm. • In some cases, the lever arm is the distance from the center of mass. • For symmetrical objects the center of mass is in the center.

Torque Definition • The combination of amount of force and distance from axis is called Torque (τ). • A torque is necessary in order to provide angular acceleration. • τ = FrsinѲ • Units = N-m • Direction = – Positive torque is clockwise (CW) – Negative torque counter-clockwise (CCW)

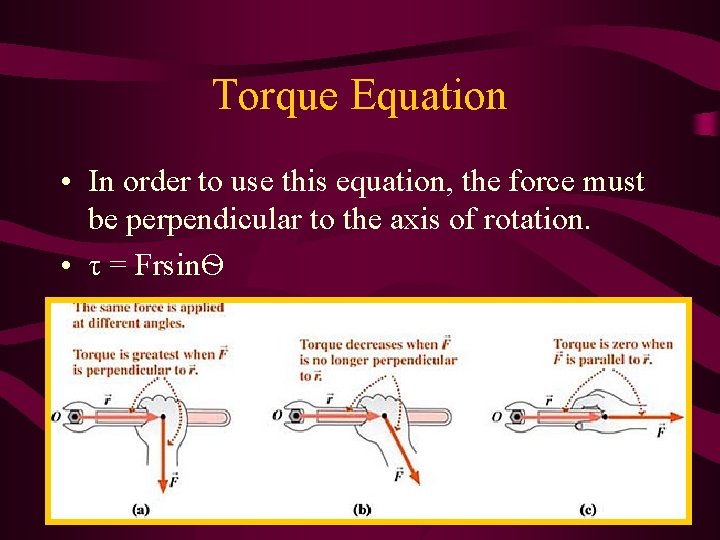
Torque Equation • In order to use this equation, the force must be perpendicular to the axis of rotation. • τ = FrsinѲ

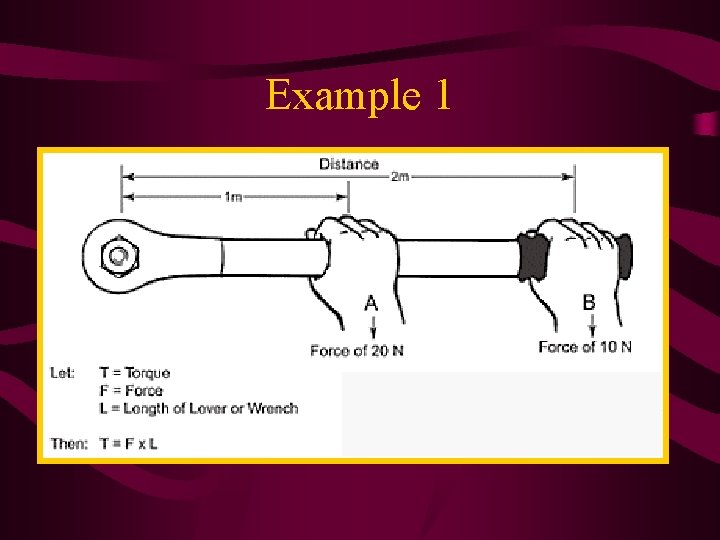
Example 1

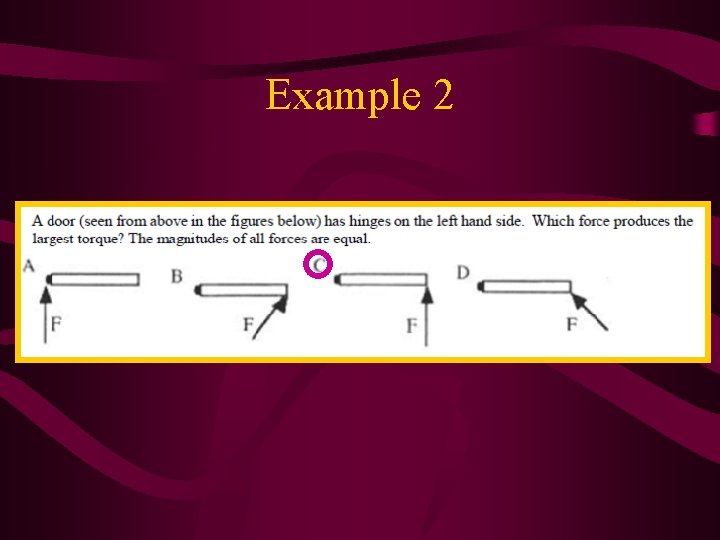
Example 2

Example 3

Rotational Equilibrium • Occurs when total torques acting balance and no rotational motion occurs. • In order for equilibrium to exist, the total torque acting in the clockwise direction must balance the total torque acting in the counterclockwise direction.

See-Saw • When stationary, the total τ clockwise is equal to the τ counterclockwise • If kid A pushes up with more force, the τ is no longer balanced and the see-saw begins to rotate clockwise with an angular velocity.

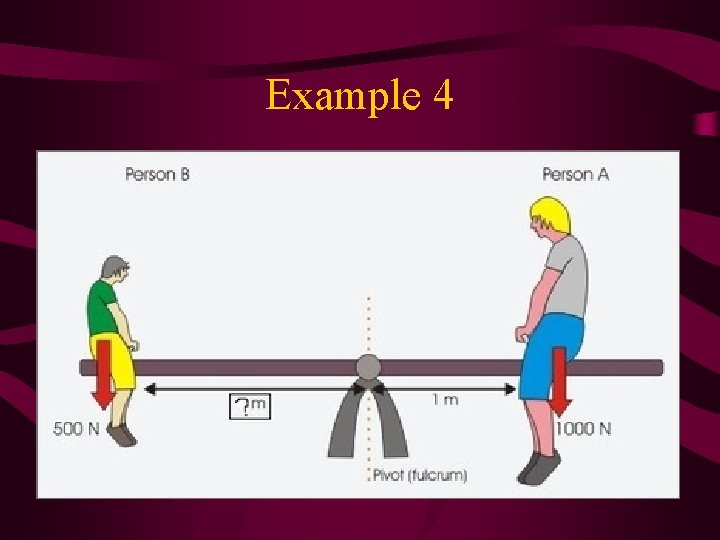
Example 4

Example 4 • • • Στ = CCW – CW = 0 Therefore, CCWτ = CWτ CCWτ = Person A = Fr = (500)r CWτ = Person B = Fr = (1000)(1) Setting these equal and solving for r gives: 500 r = 1000 r=2 m

Example 5

Example 4 • In this example, you have to take into account the weight of the board since the fulcrum is not under the center of mass. • CCW τ = CW τ • (900)(r) = (200)(3 -r) + (500)(6 -r) • (900)(r) = 3600 – 700(r) So the bar should be placed 2. 25 m from • 1600(r) = 3600 the left or 3. 75 m • r = 2. 25 m from the right.

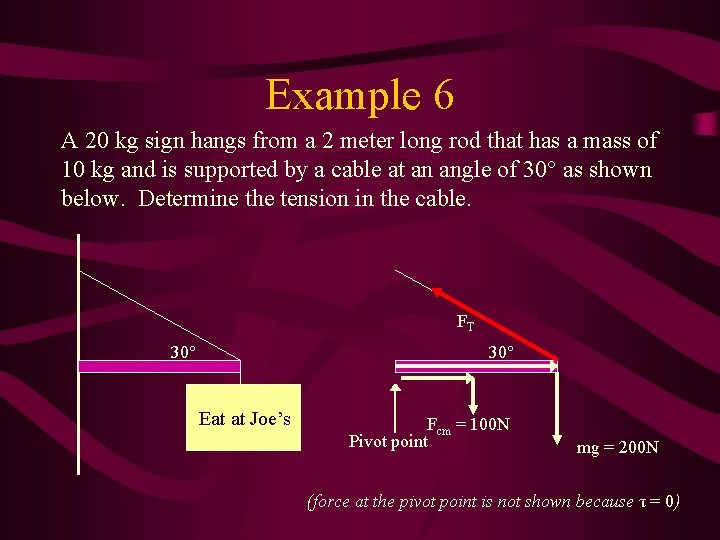
Example 6 A 20 kg sign hangs from a 2 meter long rod that has a mass of 10 kg and is supported by a cable at an angle of 30° as shown below. Determine the tension in the cable. FT 30° Eat at Joe’s Fcm = 100 N Pivot point mg = 200 N (force at the pivot point is not shown because τ = 0)

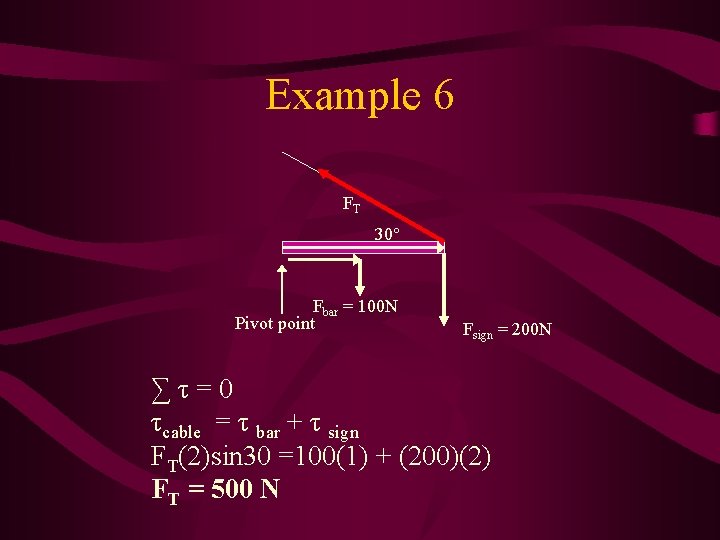
Example 6 FT 30° Fbar = 100 N Pivot point Fsign = 200 N ∑τ=0 τcable = τ bar + τ sign FT(2)sin 30 =100(1) + (200)(2) FT = 500 N