Torque and Equilibrium Chapter 8 4 problems 31

Torque and Equilibrium Chapter 8. 4 problems 31 32 Chapter 9 problems 8 10 18 26 30 22 12 13… (in order of difficulty) 1

2

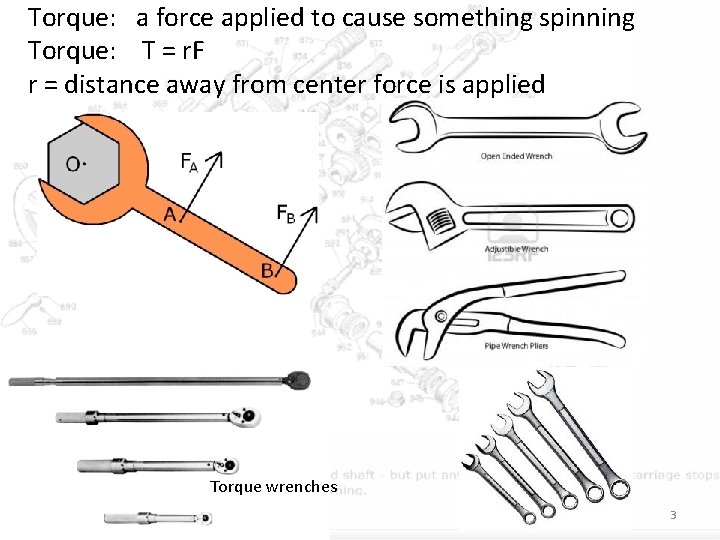
Torque: a force applied to cause something spinning Torque: T = r. F r = distance away from center force is applied Torque wrenches 3

4

OK, so you know about torque, Which set of gears is easier to use then? 5

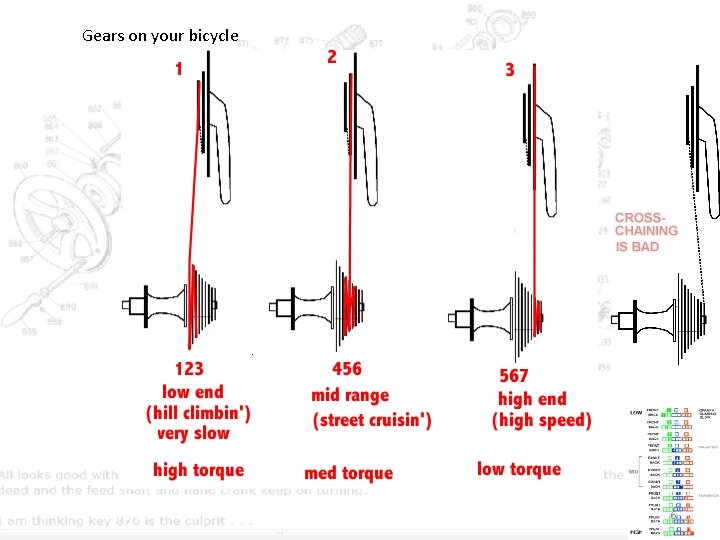
Gears on your bicycle 6

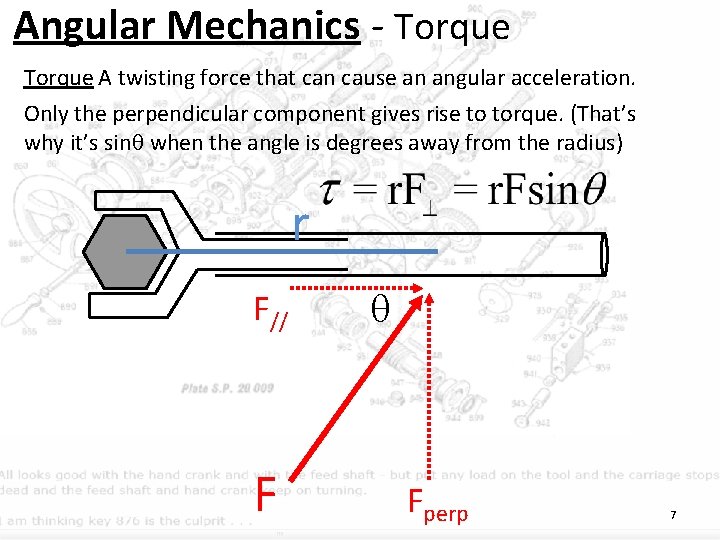
Angular Mechanics - Torque A twisting force that can cause an angular acceleration. Only the perpendicular component gives rise to torque. (That’s why it’s sin when the angle is degrees away from the radius) r F// F Fperp 7

Your big brother is trying to change a flat tire. The bolts are “froze on” and he cant’ get them off. What are some ways you could show him up? Will tying a rope to the end of a wrench result in more torque? - no, it would just bring you further away from the wrench. (unless you used it to bring something else into the system. OK, so you know about torque, Which set of gears is easier to use then on your bicycle then? 8

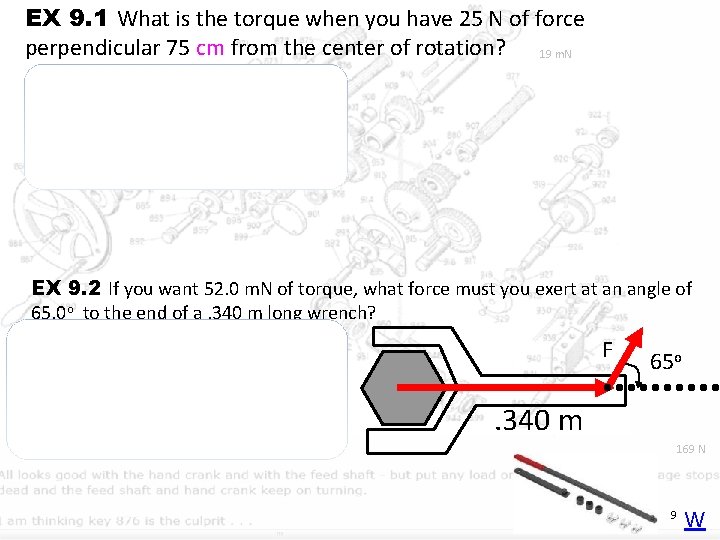
EX 9. 1 What is the torque when you have 25 N of force perpendicular 75 cm from the center of rotation? 19 m. N = r. Fsin = (. 75 m)(25 N) sin(90 o) = 18. 75 m. N EX 9. 2 If you want 52. 0 m. N of torque, what force must you exert at an angle of 65. 0 o to the end of a. 340 m long wrench? = r. Fsin F o 65 o 52 = (. 34 )(F) sin(65 ) 52 =F (. 34) sin(65 o) 168. 75 N = F 169 N . 340 m 9 W

EX 10. 1 You are trying to loosen a bolt down in the side of your engine to tighten up your power steering belt, but its hard to reach properly, so you can only pull on the wrench, from a angle 56 degrees with 16 N off of how you want. What is the torque you put on the bolt? F = 16 N 56 o r = 24 cm = r. Fsin = (. 24 m)(16 N)sin(34 o) = 2. 1 Nm because the angle from the radius is 90 – 56 = 34 EX 10. 2 The axle nut of a Volkswagen requires 200. foot pounds to loosen. 1. 38 feet How far out (in feet) do you stand on the horizontal wrench if you weigh 145 lbs? = r. F 200. ft lbs = (r)(145 lbs) (200. ft lbs)/(145 lbs) = r 1. 3793 feet = r 10

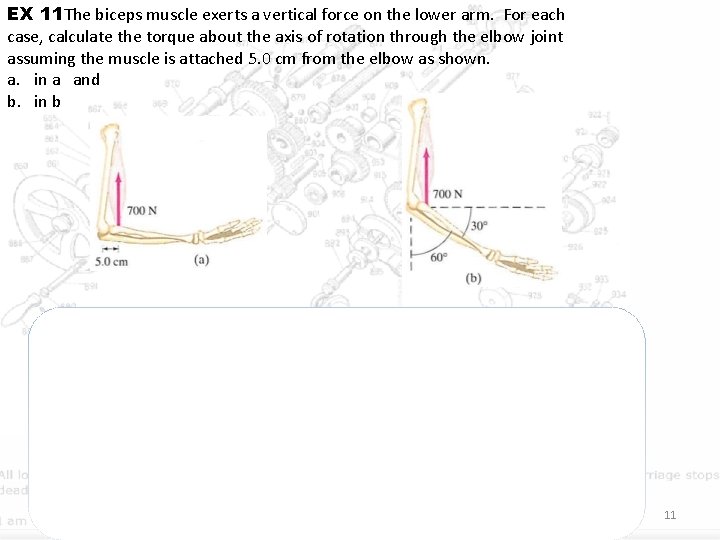
EX 11 The biceps muscle exerts a vertical force on the lower arm. For each case, calculate the torque about the axis of rotation through the elbow joint assuming the muscle is attached 5. 0 cm from the elbow as shown. a. in a and b. in b so T= r. F = (0. 050 m)(700 N) = 35 Nm. T=r. Fsin(θ) = (0. 050 m)(0. 866)(700 N) = 30 Nm. The arm can exert less torque at this angle. Weight machines at gyms are often designed to take this variation with angle into account. 11

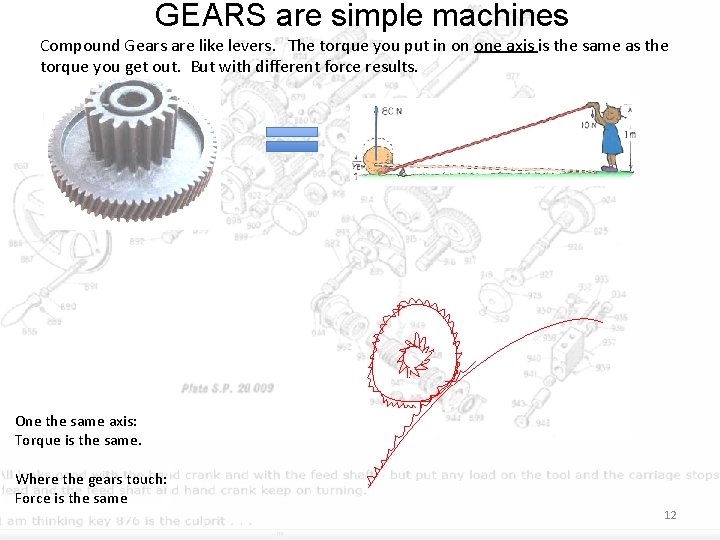
GEARS are simple machines Compound Gears are like levers. The torque you put in on one axis is the same as the torque you get out. But with different force results. One the same axis: Torque is the same. Where the gears touch: Force is the same 12

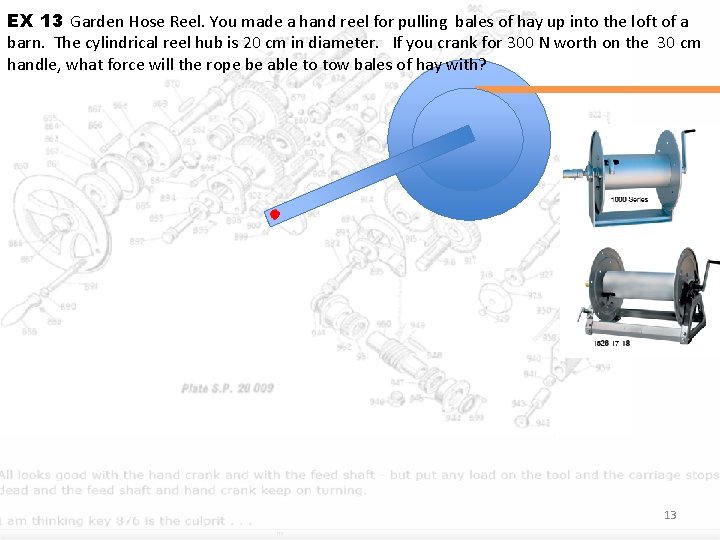
EX 13 Garden Hose Reel. You made a hand reel for pulling bales of hay up into the loft of a barn. The cylindrical reel hub is 20 cm in diameter. If you crank for 300 N worth on the 30 cm handle, what force will the rope be able to tow bales of hay with? 13

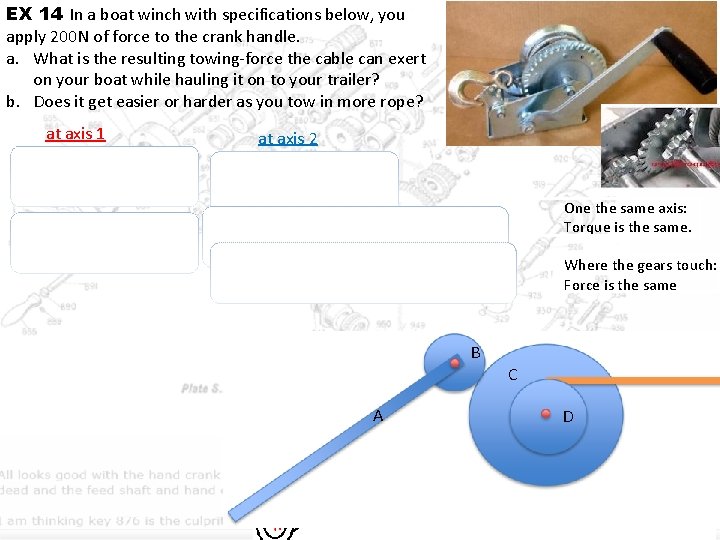
EX 14 In a boat winch with specifications below, you apply 200 N of force to the crank handle. a. What is the resulting towing-force the cable can exert on your boat while hauling it on to your trailer? b. Does it get easier or harder as you tow in more rope? at axis 1 at axis 2 One the same axis: Torque is the same. because Fc = FB Where the gears touch: Force is the same B A C D 14

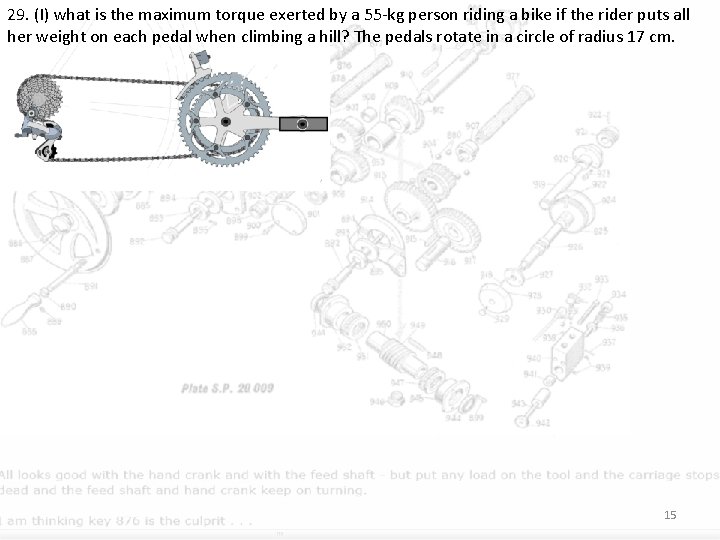
29. (I) what is the maximum torque exerted by a 55 -kg person riding a bike if the rider puts all her weight on each pedal when climbing a hill? The pedals rotate in a circle of radius 17 cm. 15

CENTER OF MASS and EQUILIBRIUM. CENTER OF MASS/GRAVITY: is always at the middle of objects with even density and symmetric volume. FULCRUM ( ): - the point or axis of rotation at which an object will swing about (especially in tipping over) - any point holding an object up is a fulcrum (so an object can have more than one fulcrum) - also, if an object stands on a flat base, anywhere on the edge of the base can act as a fulcrum WEIGHT AS A TORQUE: Unless an object’s center of mass is above the fulcrum, the weight of an object is causing torque on it. EQUILIBRIUM : when the net force is zero AND when the net torque about any fulcrum is zero. center of mass = length / 2 17

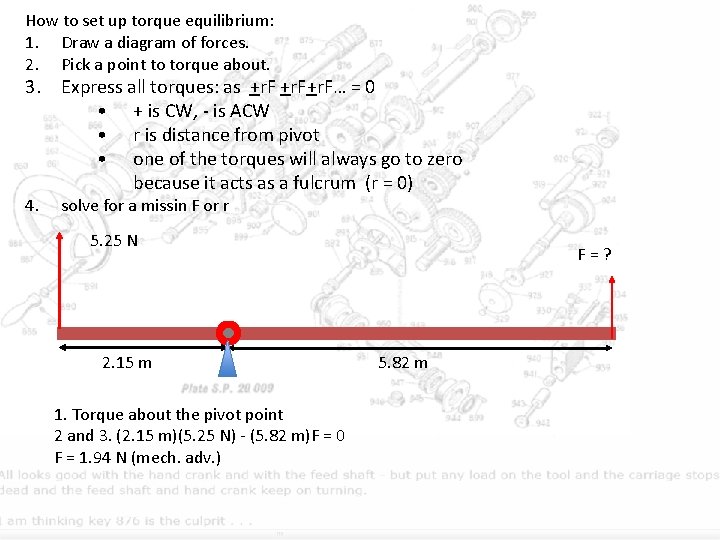
How to set up torque equilibrium: 1. Draw a diagram of forces. 2. Pick a point to torque about. 3. Express all torques: as +r. F+r. F… = 0 • + is CW, - is ACW • r is distance from pivot • one of the torques will always go to zero because it acts as a fulcrum (r = 0) 4. solve for a missin F or r 5. 25 N 2. 15 m 1. Torque about the pivot point 2 and 3. (2. 15 m)(5. 25 N) - (5. 82 m)F = 0 F = 1. 94 N (mech. adv. ) F=? 5. 82 m

A 17 O-cm-tall person lies on a light (massless) board which is supported by two scales, one under the feet and one under the top of the head. The two scales read, respectively, 31. 6 and 35. 1 kg. Where is the center of mass of this person? STEP 1. determine net forces on lever ∑F = 0 F 1 - Fmg + F 2 = 0 F 1 - W + F 2 = 0 STEP 0. draw a free body diagram of all the forces acting on the lever. STEP 2. Determine torque about pivot point (turn net force equation into net torque) Torque about the left side ∑τ = 0 0 = 0 - τmg + τ2 0 = W (r) + F 2(170) 0 = (35. 1+31. 6)(9. 8)(r) + 31. 6(9. 8)(170) = r (35. 1+31. 6)(9. 8) 80. 54 cm = r 19

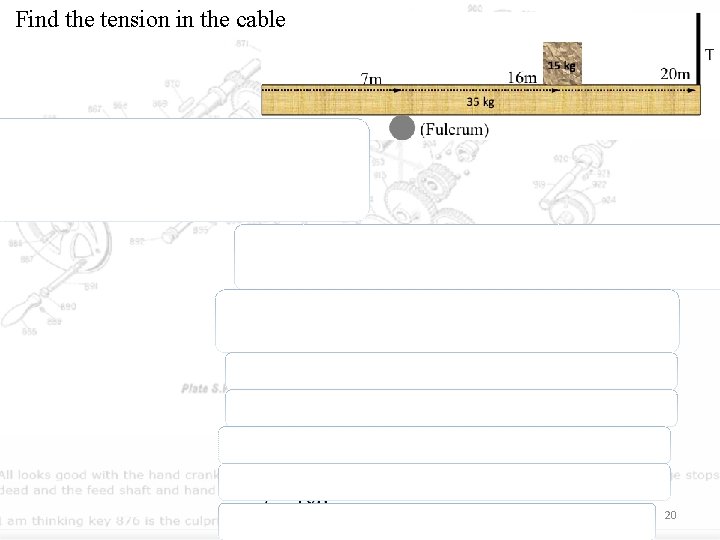
Find the tension in the cable since net force is… the torque about the hinge is … 20

21

There is a cable-drawn bridge that needs to hold up a heavy crate. What will the Tension in the cable be given that the situation below is in equilibrium? since net force is… ⁰ 350 kg the torque about the hinge is … 22

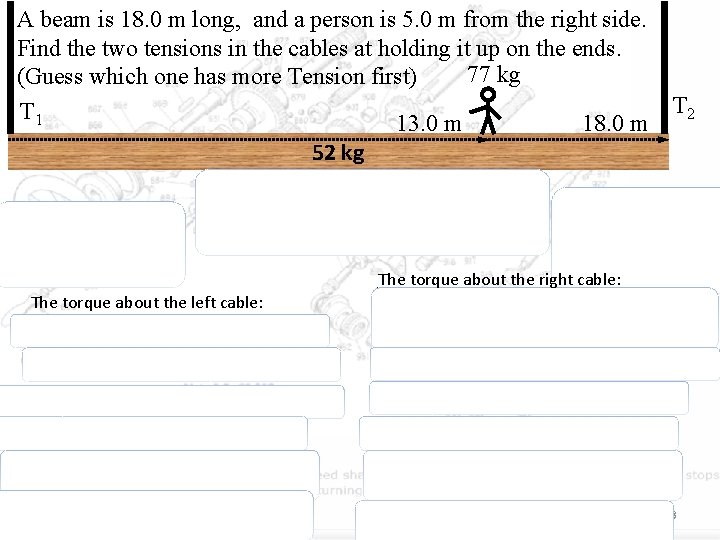
A beam is 18. 0 m long, and a person is 5. 0 m from the right side. Find the two tensions in the cables at holding it up on the ends. 77 kg (Guess which one has more Tension first) T 1 13. 0 m 18. 0 m T 2 52 kg T 2 Wb Wp T 1 Wb Wp The torque about the right cable: The torque about the left cable: 23

A ladder leans against a wall at apoint 4. 0 m above the ground as shown. The ladder is 5. 0 -m-Iong and has mass 12. 0 kg. Assuming the wall is frictionless but the ground is not, determine the forces exerted on the ladder by the ground and the wall. y-direction ∑Fy = 0 Ffloor y - Fmg = 0 x- direction ∑Fx = 0 Ffloor x - Fwall x = 0 Ffloor y = Fmg = 12(9. 8) Ffloor y = Fmg = 118 N which sends us off to… Torque from the foot of the ladder ∑τ = 0 0 = τ mg - τ wall x 0 = F˔mg (1. 5) – F ˔wall x (5) 0 = mg sin(θ )(1. 5) – Fwall x sin(φ)(5) 0 = mg sin(53 )(1. 5) – Fwall x sin(37)(5) 12(9. 8) sin(53 )(1. 5) = Fwall x sin(37)(5) 44 N = Fwall x finding θ because 345 triangle: tan-1(4/3) =θ 53 = θ and then 37 = φ 24

25

26