TopologyAware Distributed Graph Processing for Tightly Coupled Clusters

Topology-Aware Distributed Graph Processing for Tightly -Coupled Clusters Mayank Bhatt, Jayasi Mehar DPRG: http: //dprg. cs. uiuc. edu

Our work explores the problem of graph partitioning, focused on reducing the communication cost on tightly coupled clusters 2

Why? • Experimenting with cloud frameworks on HPC systems • Interest in supercomputing as a service • More big data jobs running on supercomputers 3

Tightly-Coupled Clusters • Supercomputers • Compute nodes embedded inside the network topology • Messages routed via compute nodes • Communication patterns can influence performance • “Hop count” is an approximate measure of cost of communication 4

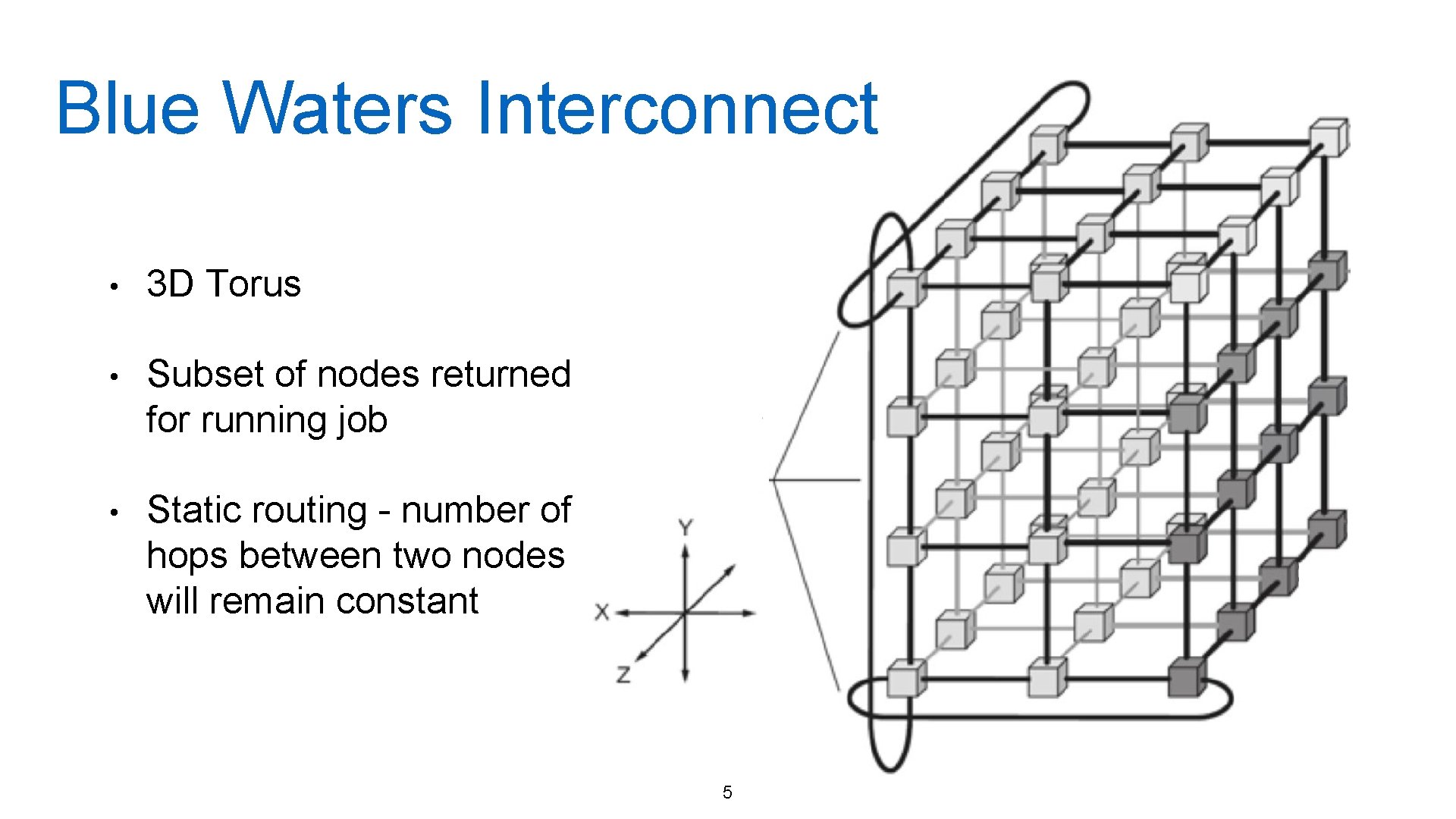
Blue Waters Interconnect • 3 D Torus • Subset of nodes returned for running job • Static routing - number of hops between two nodes will remain constant 5

Graph Processing Systems • Lot of real world data is expressed in the form of graphs • Billion of vertices, trillions of edges, need to distribute • Algorithms - ex. Shortest path, Page. Rank • 2 stages - Ingress and Processing 7

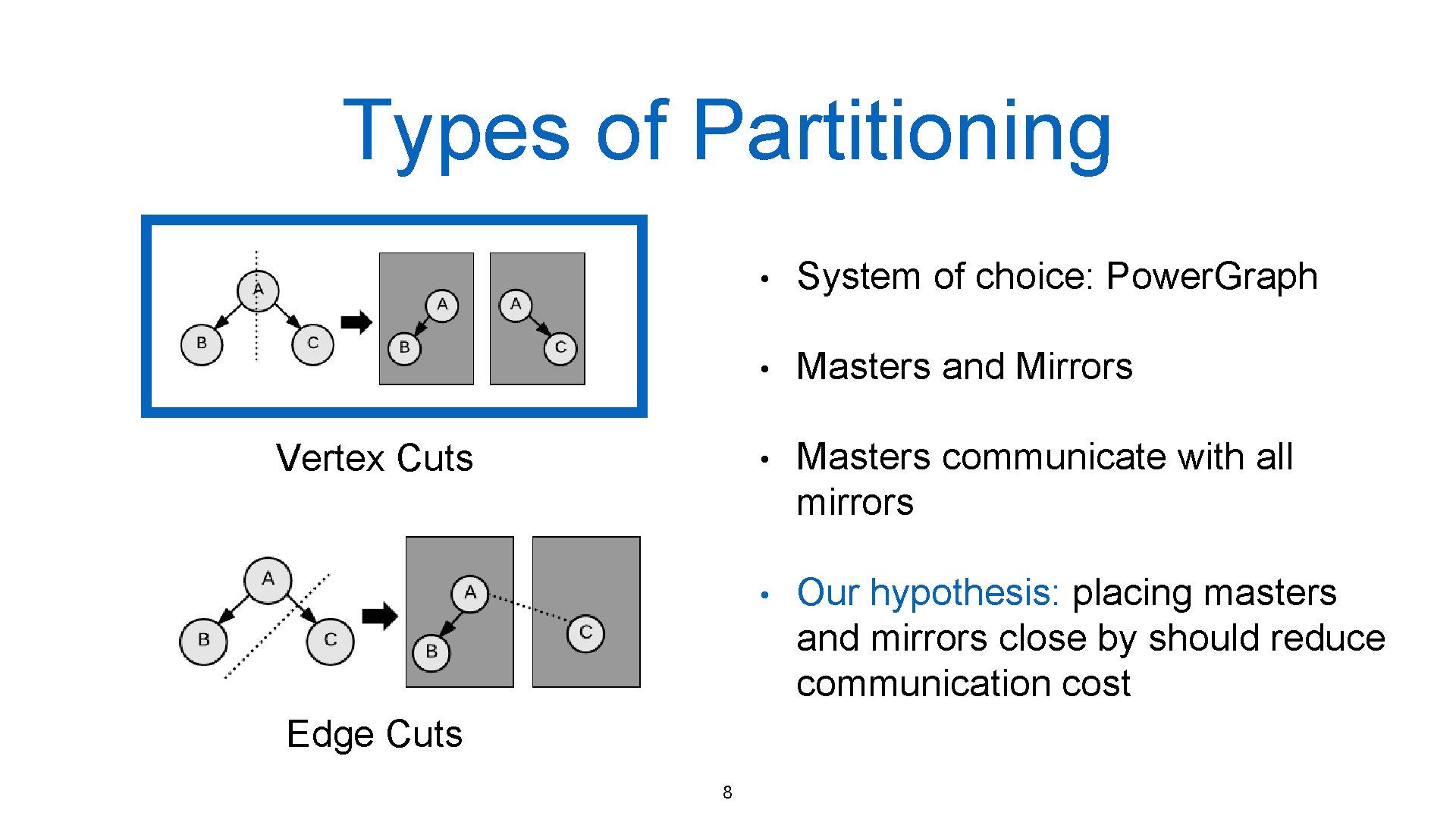
Types of Partitioning Vertex Cuts Edge Cuts 8 • System of choice: Power. Graph • Masters and Mirrors • Masters communicate with all mirrors • Our hypothesis: placing masters and mirrors close by should reduce communication cost

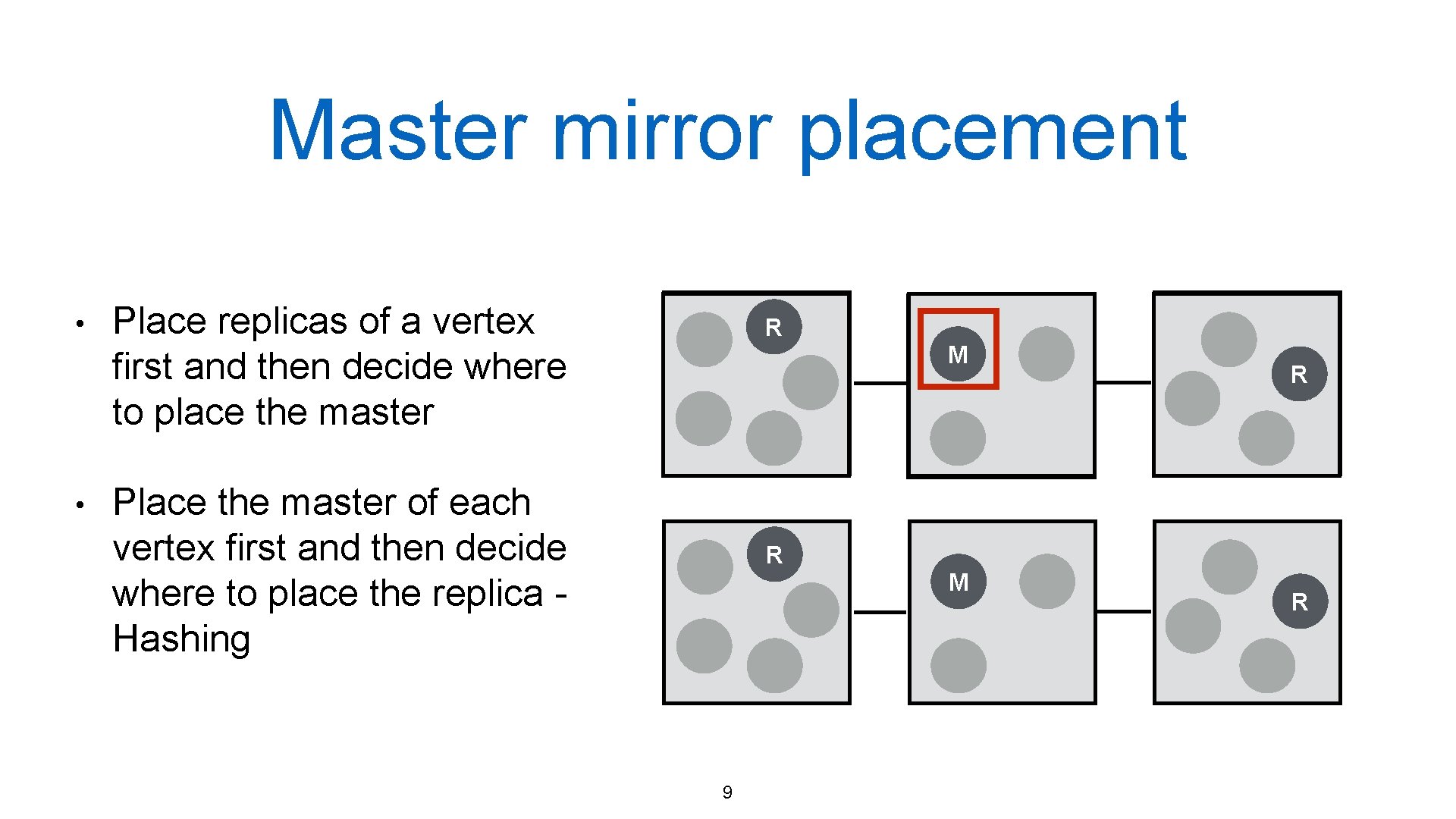
Master mirror placement • • Place replicas of a vertex first and then decide where to place the master R M Place the master of each vertex first and then decide where to place the replica Hashing R R M 9 R

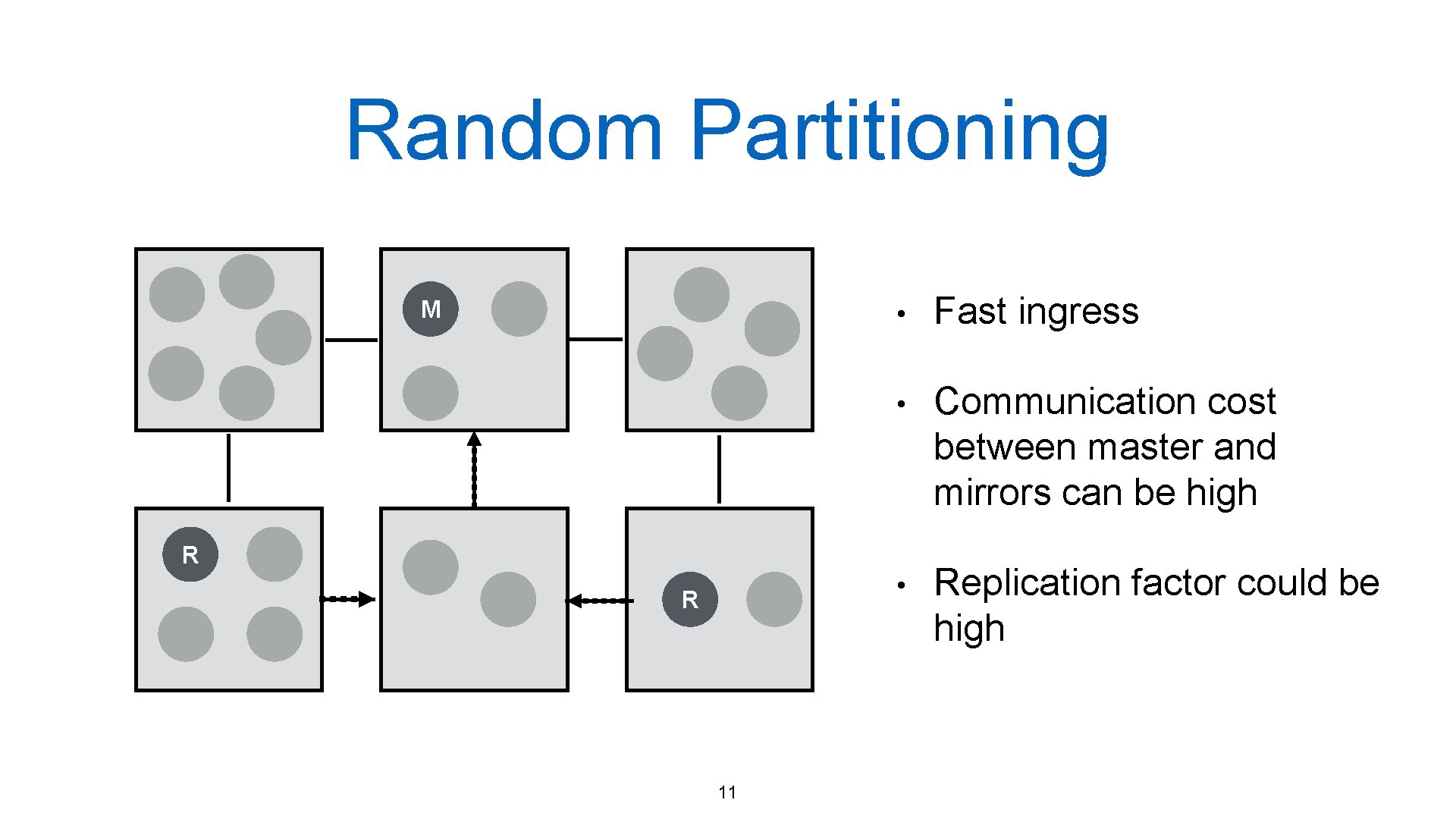
Random Partitioning M • Fast ingress • Communication cost between master and mirrors can be high • Replication factor could be high R R 11

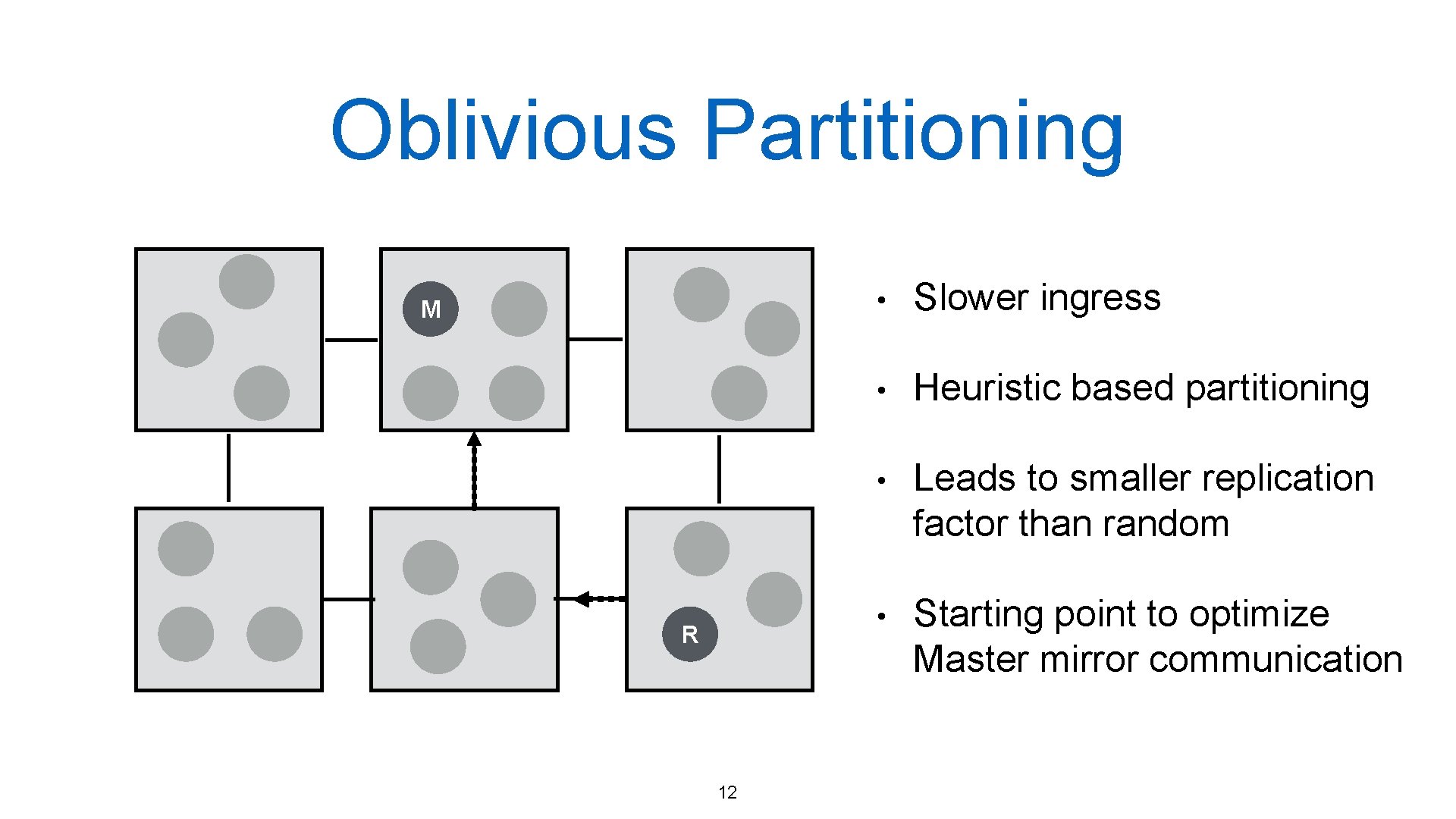
Oblivious Partitioning M R 12 • Slower ingress • Heuristic based partitioning • Leads to smaller replication factor than random • Starting point to optimize Master mirror communication

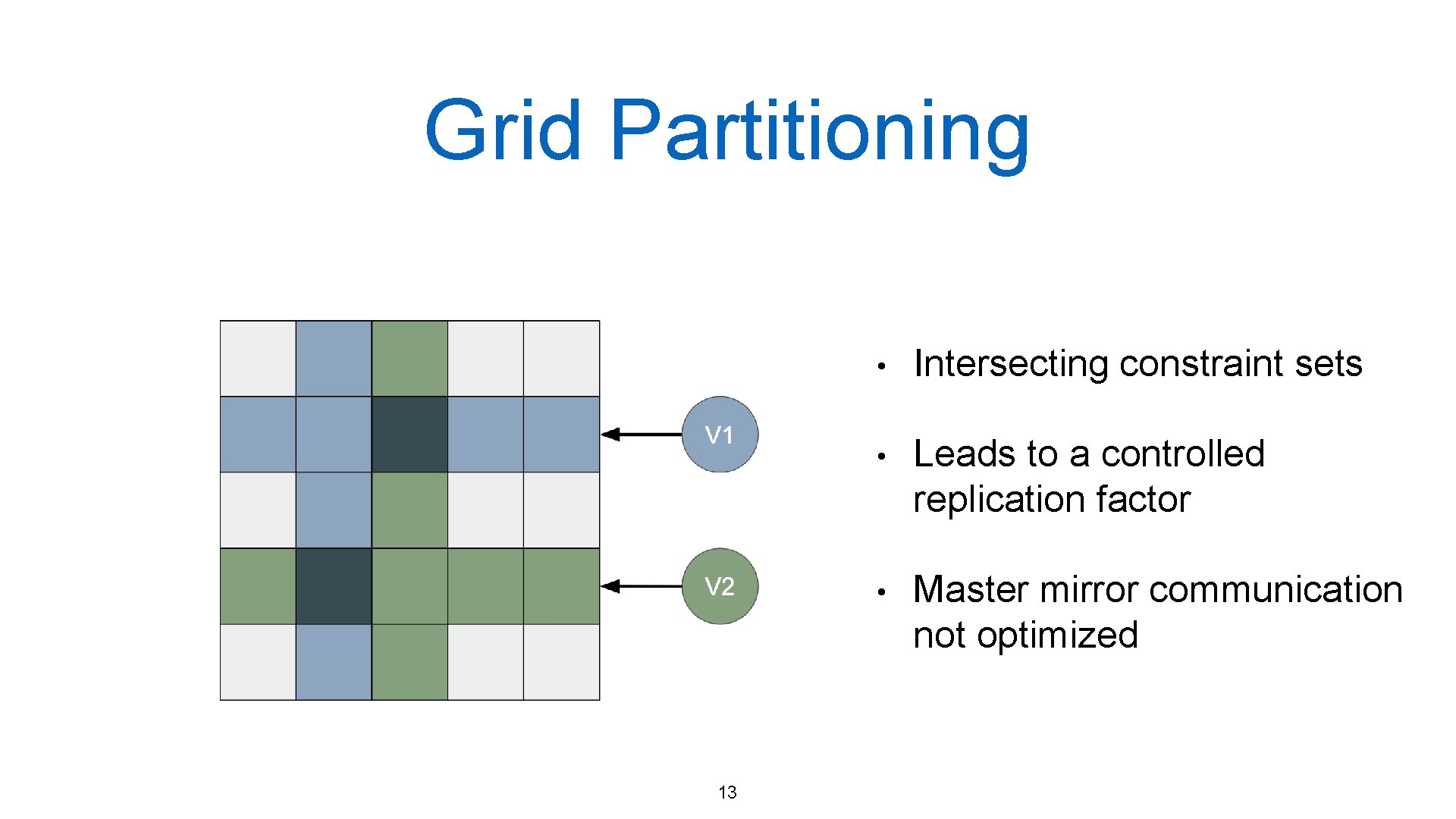
Grid Partitioning 13 • Intersecting constraint sets • Leads to a controlled replication factor • Master mirror communication not optimized

Topology Aware Variants • Make the partitioning step aware of the underlying network topology • Place masters and mirrors such that communication cost is minimized 14

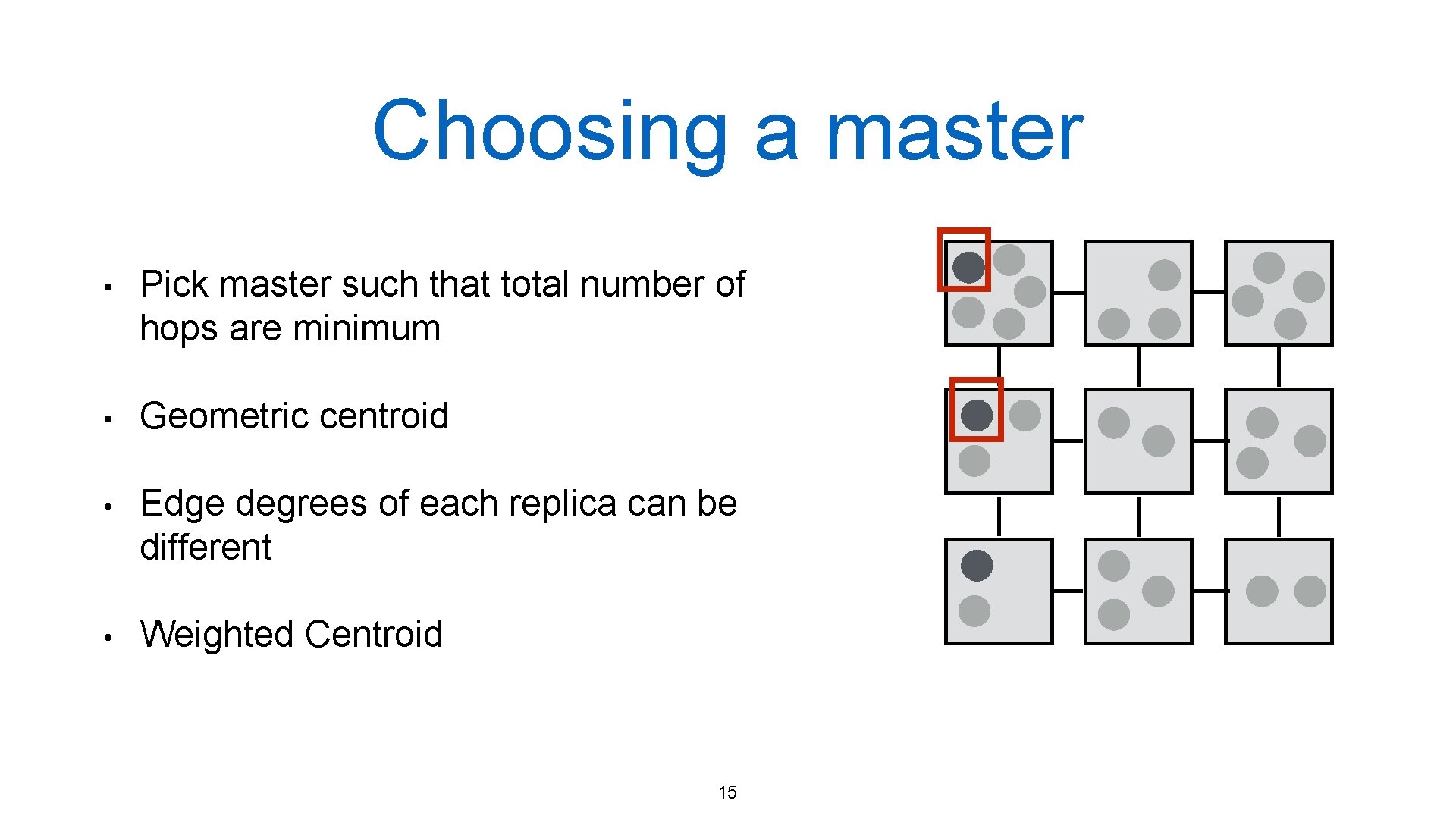
Choosing a master • Pick master such that total number of hops are minimum • Geometric centroid • Edge degrees of each replica can be different • Weighted Centroid 15

Grid Centroid Edges are placed using the Grid partitioning Strategy first Number of hops between mirror and candidate Number of edges on mirror 16 Load: number of masters on candidate

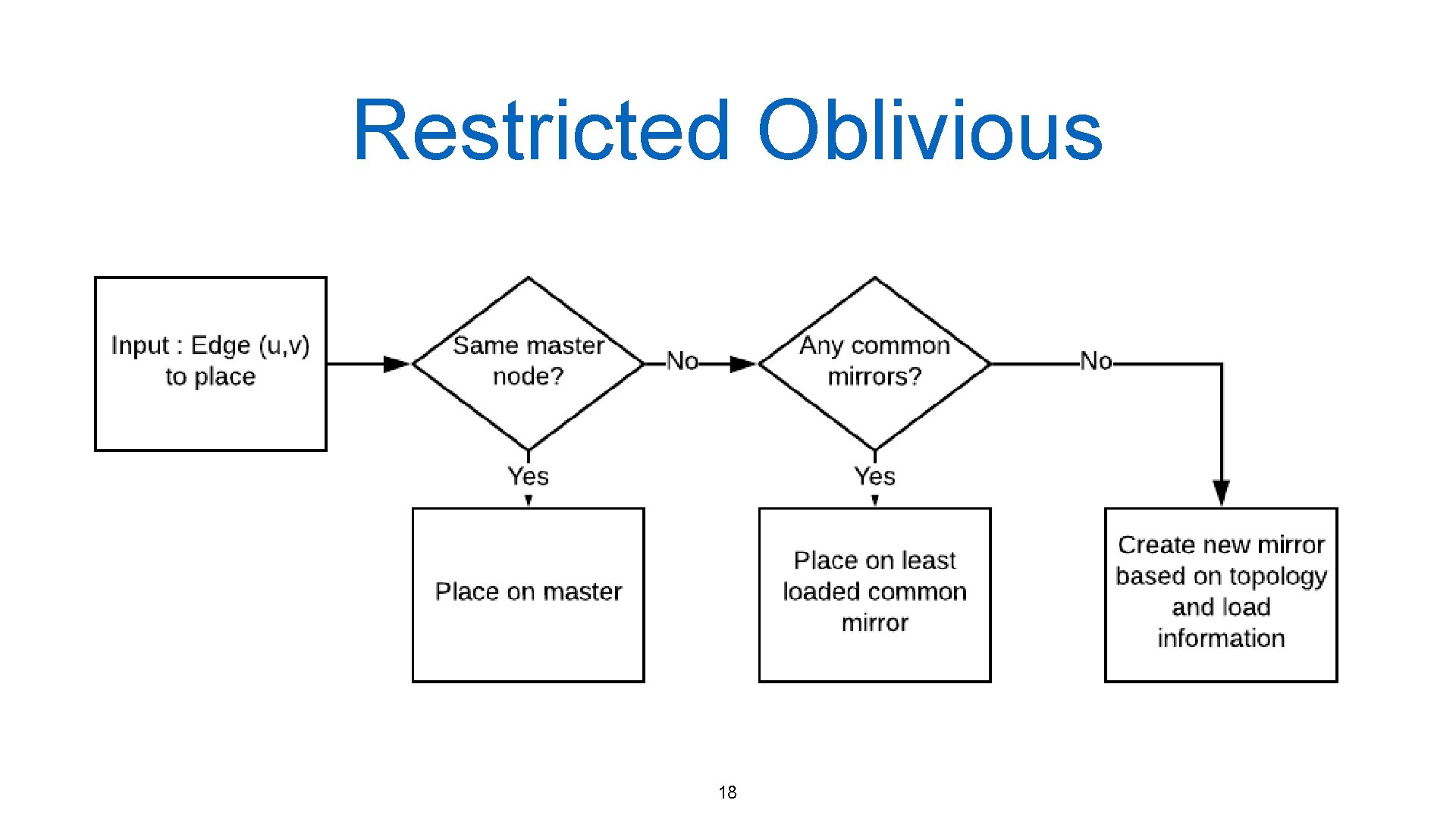
Restricted Oblivious 18

Restricted Oblivious Maximum number of edges on a node Number of edges on candidate Minimum number of edges on a node Number of hops between candidate and master 19

Experiments • Cluster size: 36 nodes • Algorithm: Approximate diameter • Graph: Power-law, 20 million vertices 20

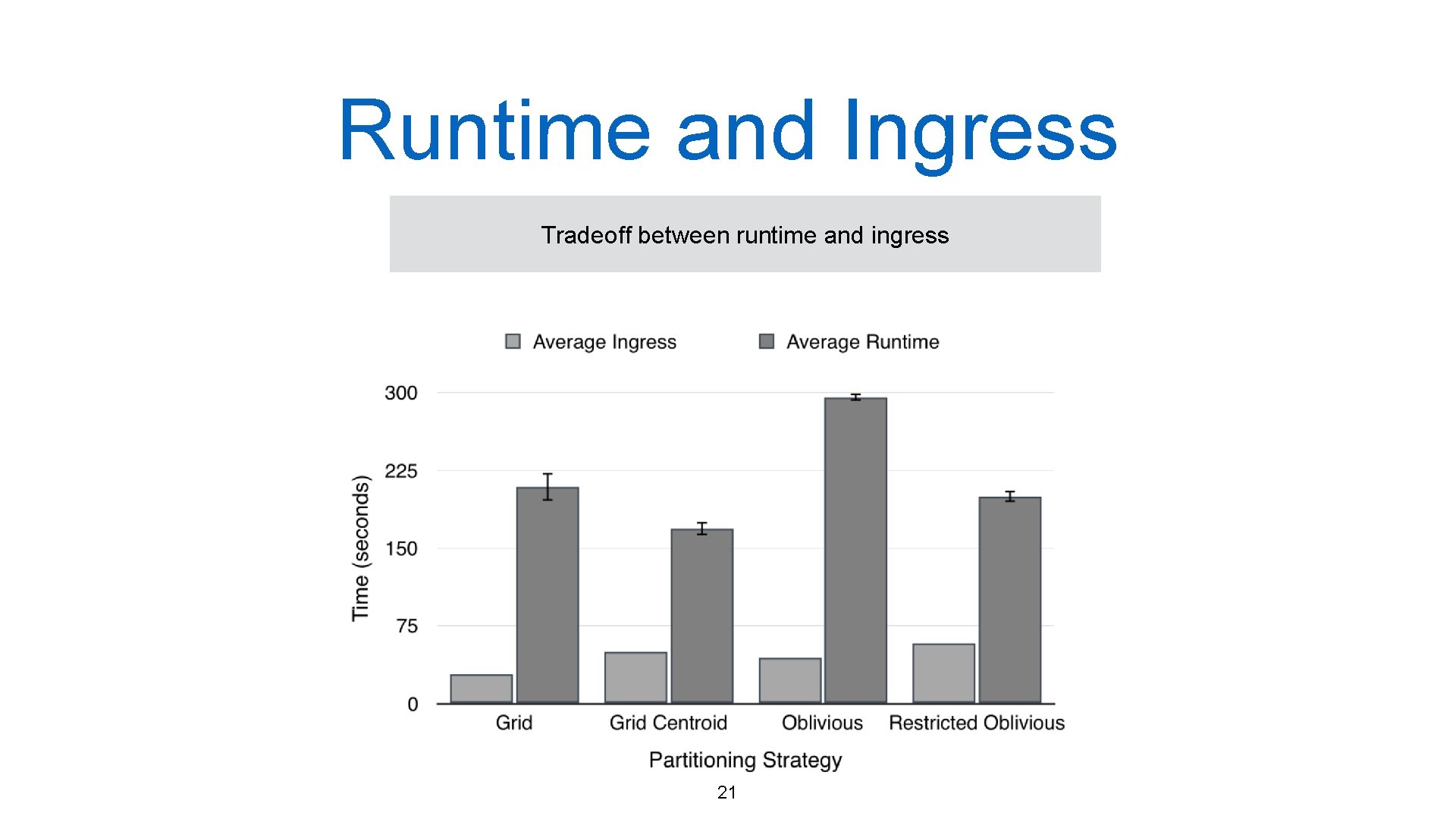
Runtime and Ingress Tradeoff between runtime and ingress 21

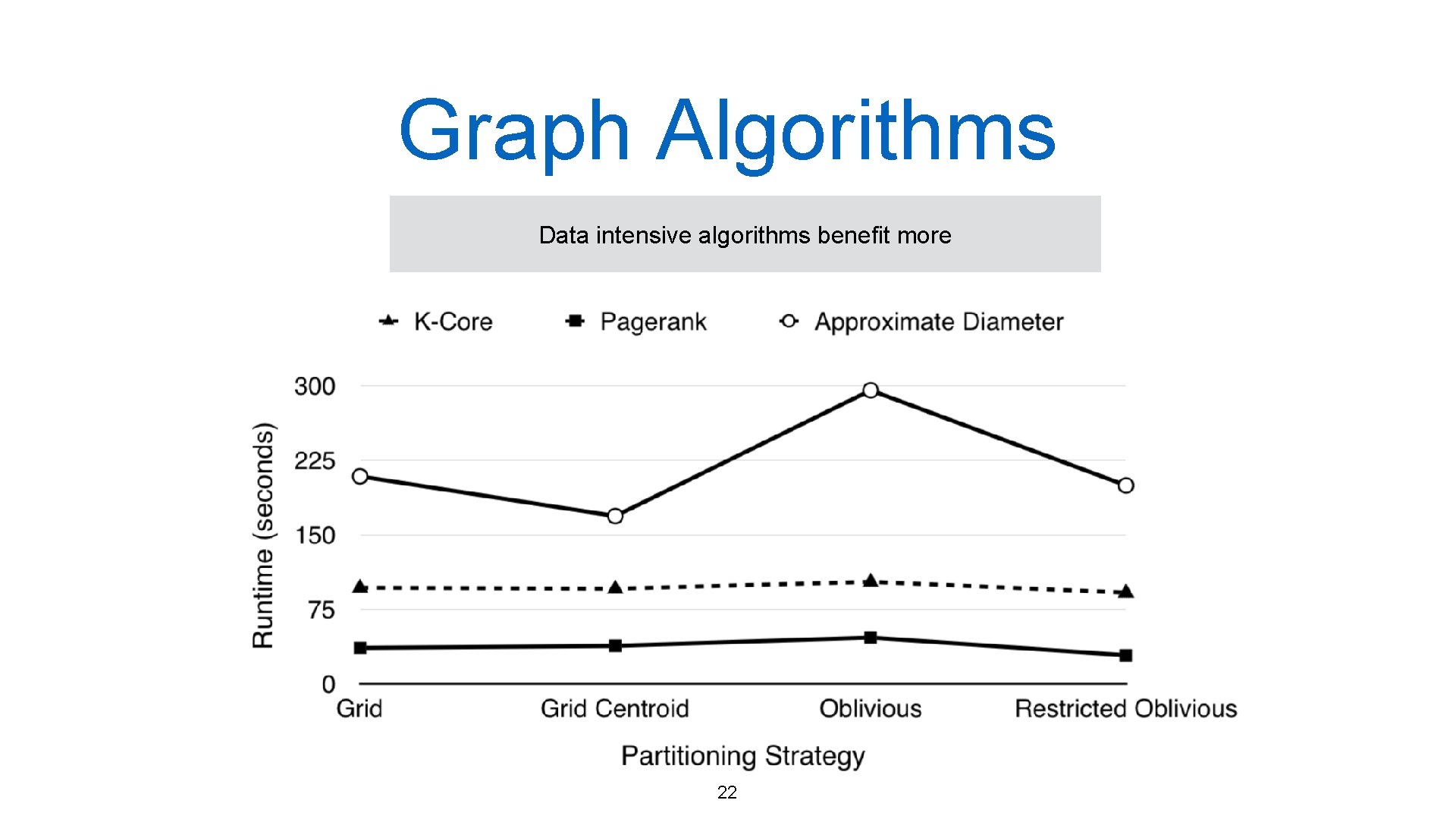
Graph Algorithms Data intensive algorithms benefit more 22

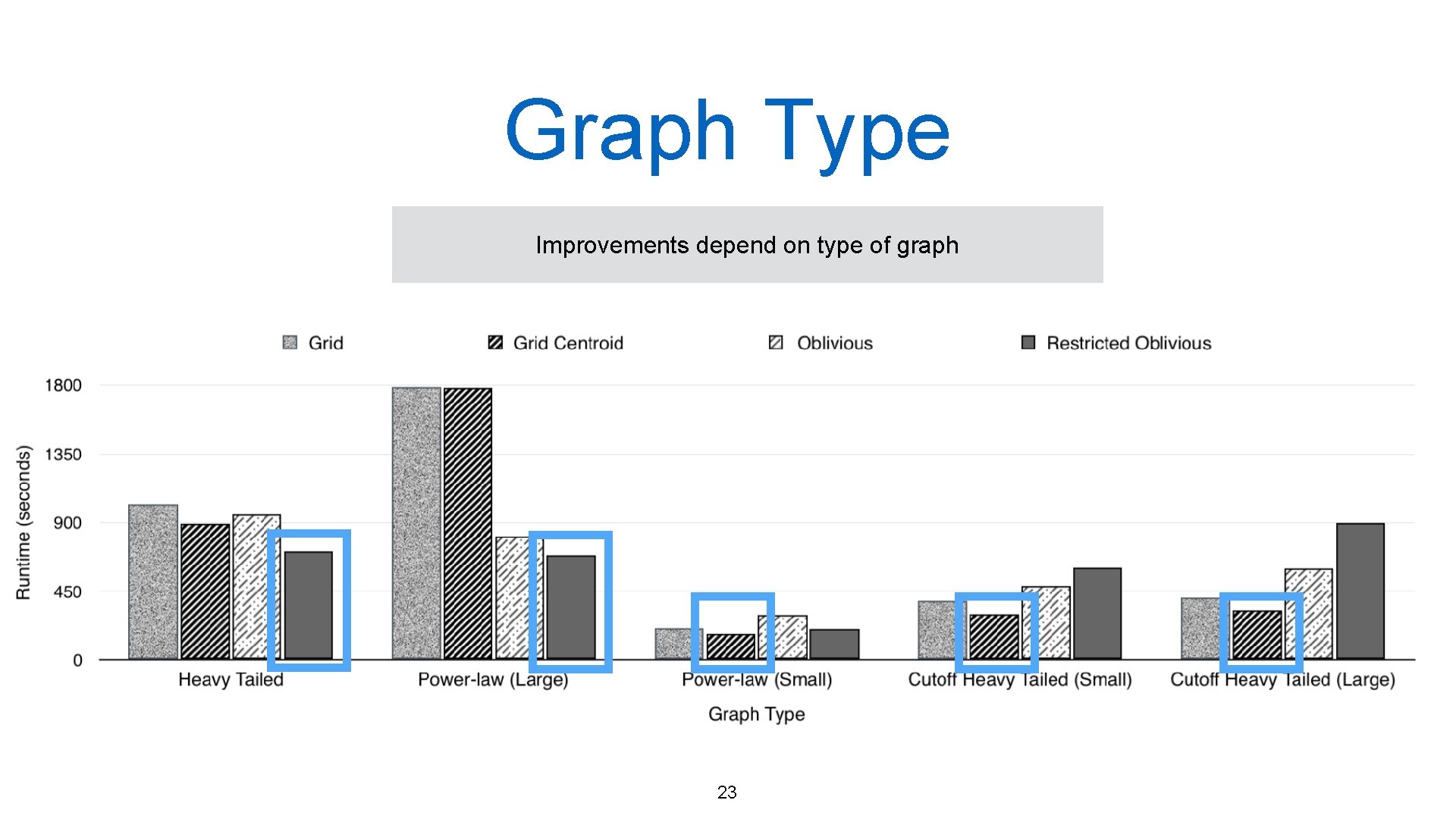
Graph Type Improvements depend on type of graph 23

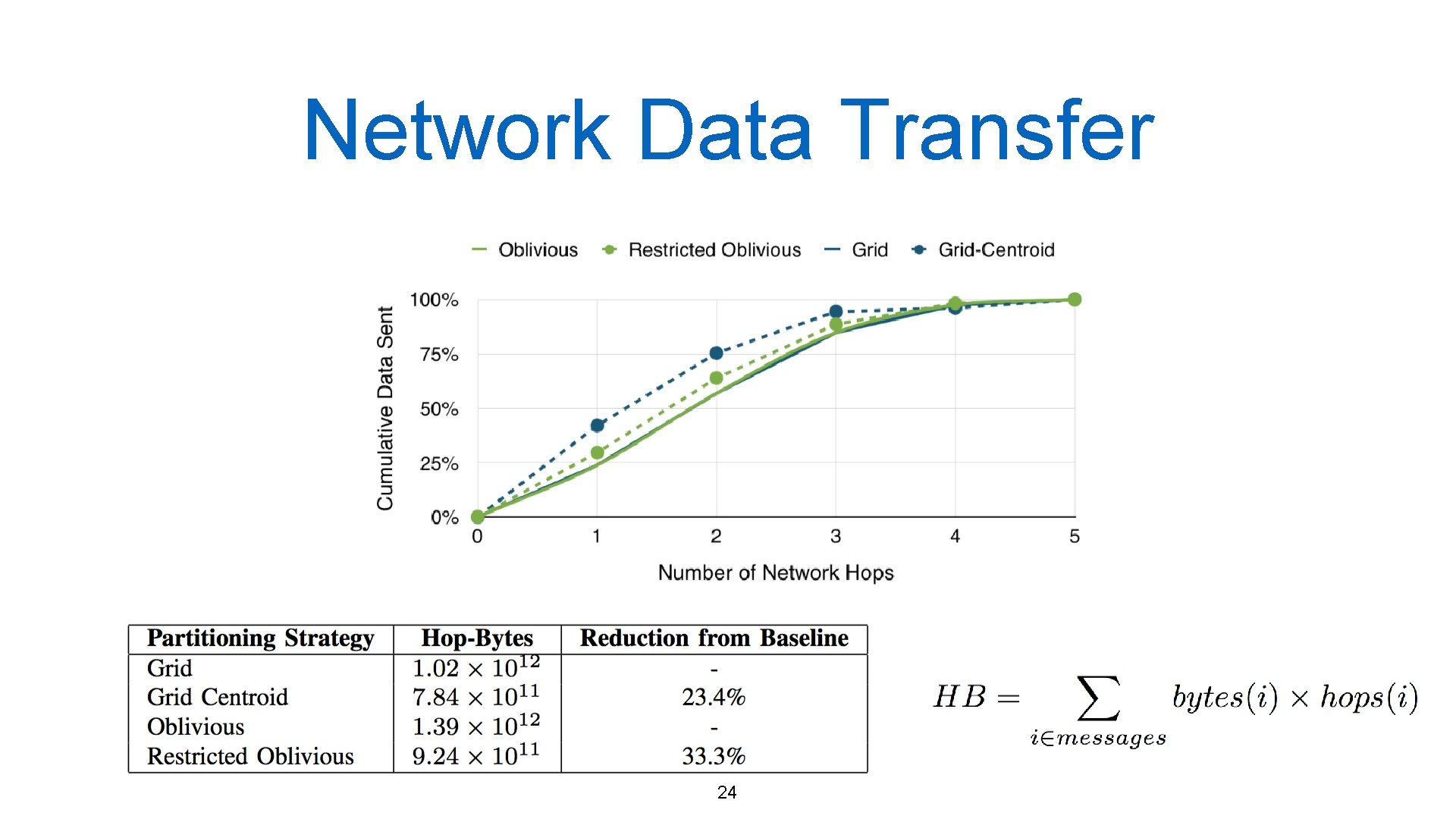
Network Data Transfer 24

Other System Optimizations • Controlling the frequency of data injection into network impacts runtime in certain algorithms • Smaller network buffers => flushed more frequently 25

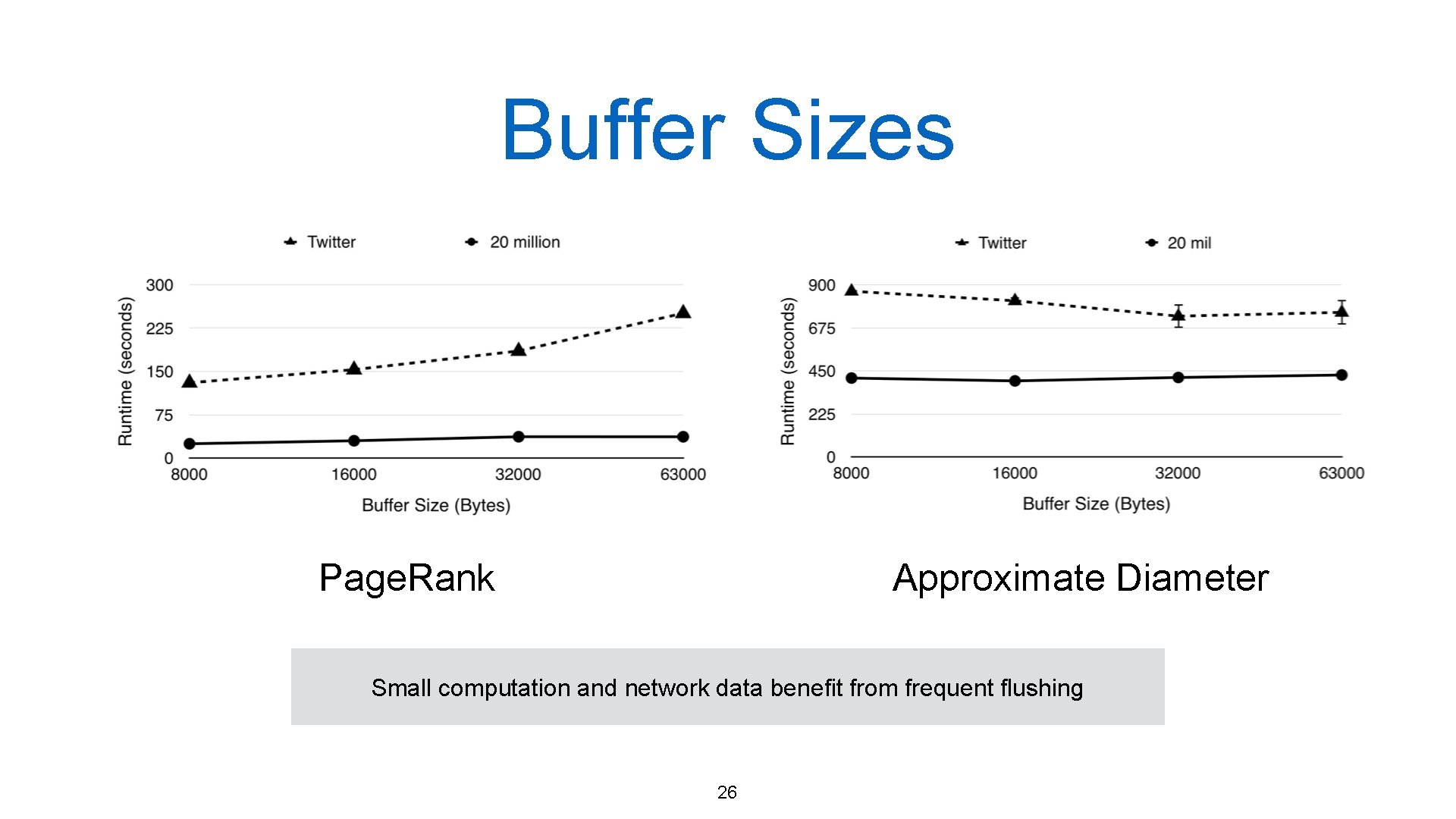
Buffer Sizes Page. Rank Approximate Diameter Small computation and network data benefit from frequent flushing 26

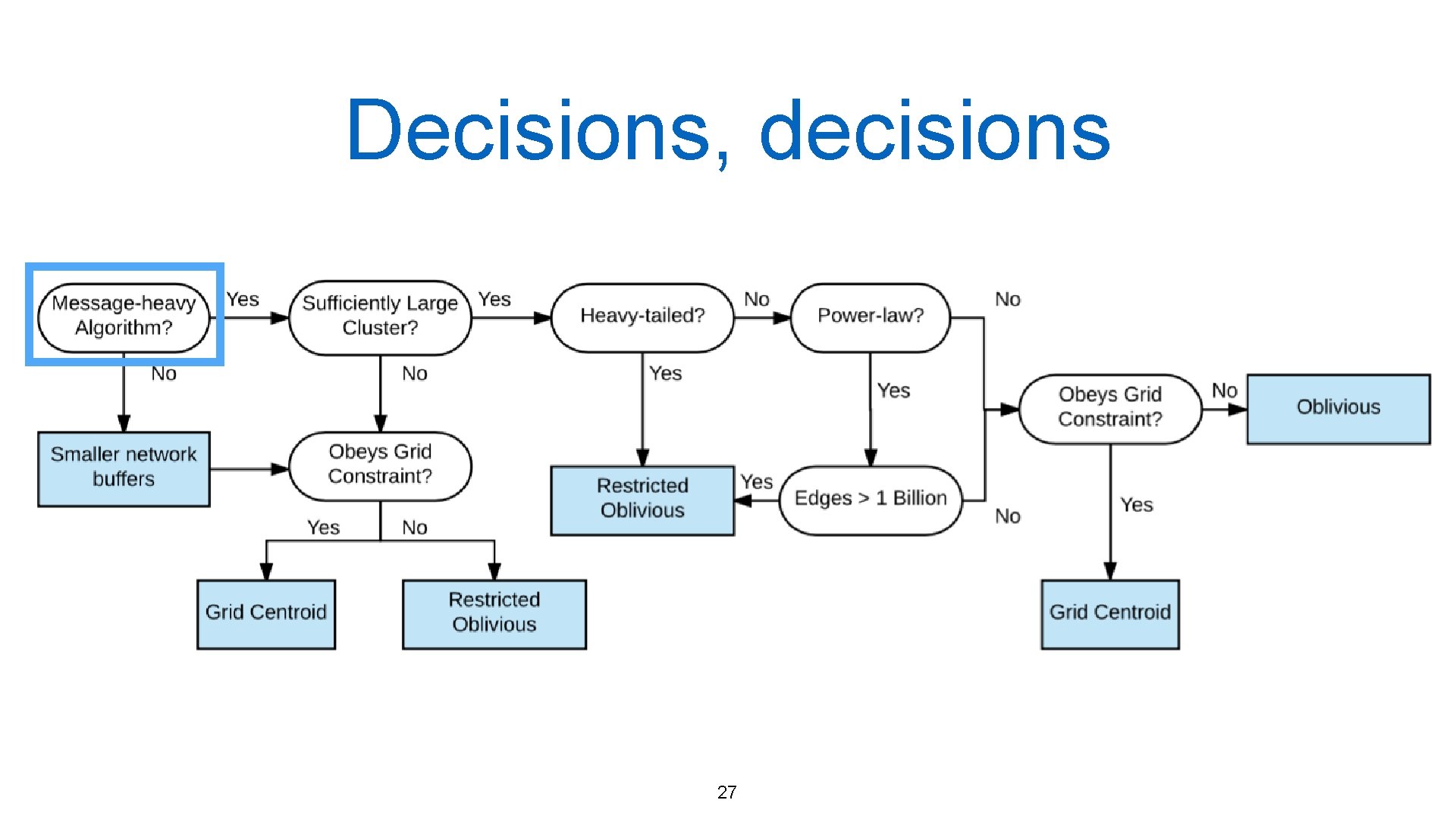
Decisions, decisions 27

Conclusions • Two new topology-aware algorithms for graph partitioning • No ‘one size fits all’ approach to graph partitioning • We propose a decision tree that can help decide which partitioning algorithm is best • System optimizations complement performance DPRG: http: //dprg. cs. uiuc. edu 28

Questions and Feedback? DPRG: http: //dprg. cs. uiuc. edu 29