Topology optimization pages from Bendsoe and Sigmund and

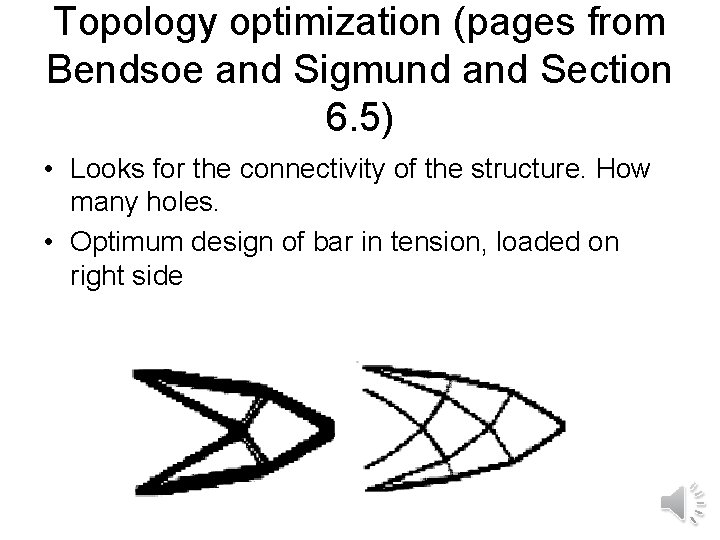
Topology optimization (pages from Bendsoe and Sigmund and Section 6. 5) • Looks for the connectivity of the structure. How many holes. • Optimum design of bar in tension, loaded on right side

Structural Optimization categories • Fig. 1. 1

Problem optimization classification • Provide examples of sizing, shape, and topology optimization in the design of a car structure.

History • Microstructure based approach by various mathematicians in the 1970 s and early 1980 s • Engineers caught on after landmark paper of Martin Bendsoe of the Technical University of Denmark and Noboru Kikuchi of the University of Michigan in 1988 • Method dominated by Danes • Alternative based on simpler mathematics called Evolutionary Structural Optimization developed by Australians Mike Xie and Grant Steven in mid 1990 s.

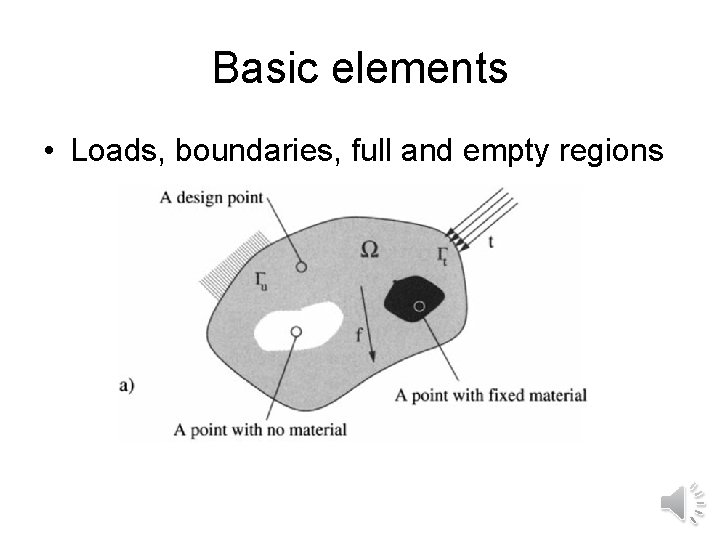
Basic elements • Loads, boundaries, full and empty regions

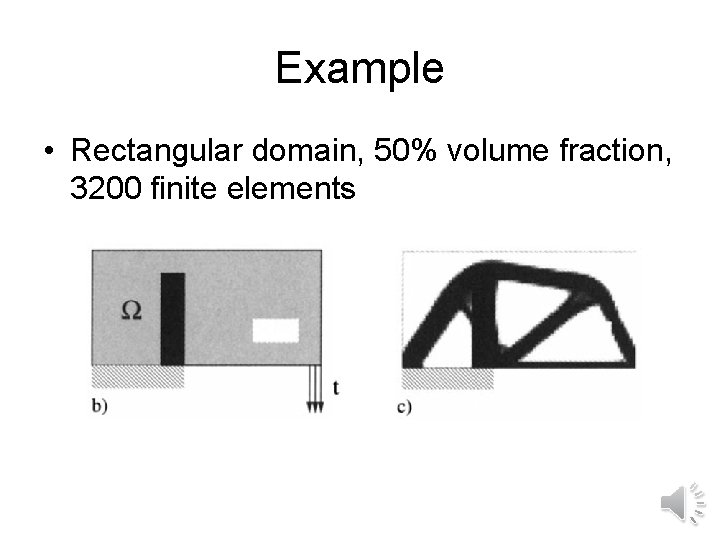
Example • Rectangular domain, 50% volume fraction, 3200 finite elements

Design freedom • Goal is to specify the region there is material where • Simplifications: The same material everywhere, and it is isotropic

Challenge and answer • We will divide domain into large numbers of elements (pixels or voxels) and will have a binary decision for each. • With 10, 000 elements, there are 210, 000 possible designs! • Answer 1: Find trick to convert to continuous design (so can use derivatives) • Answer 2: Find objective function with cheap derivatives.

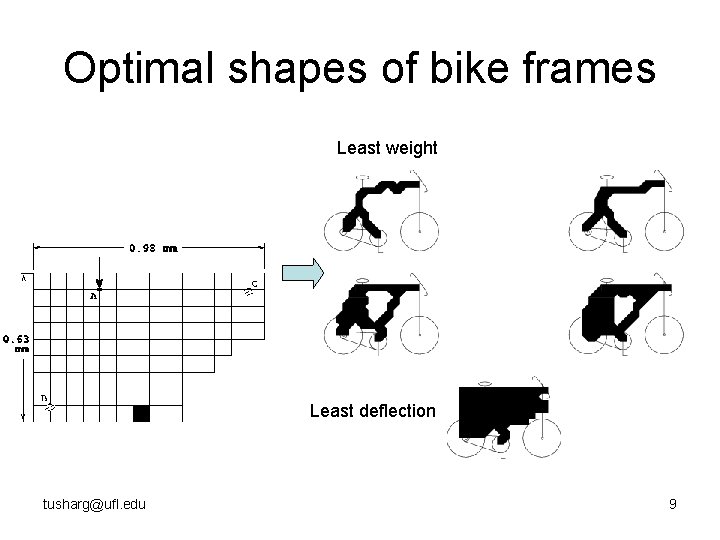
Optimal shapes of bike frames Least weight Least deflection tusharg@ufl. edu 9

Solid Isotropic Material with Penalization (SIMP) • Micro structure leads to power-law where elastic moduli vary like power of density • Later it turned out that microstructure is not necessary, just SIMP • First ingredient: Density can take any value in [0, 1]. • Second ingredient: Power law for Young modulus favors 0 -1 solution. Why?

Problem SIMP • Assume E is proportional to the square of the density. Compare the compliance of a bar in tension for a volume fraction of 0. 5 between uniform density of 0. 5 and half of the area at full density and half empty.

Compliance minimization • Compliance is the opposite of stiffness • Inexpensive derivatives

Density design variables • Recall • For density variables • Want to increase density of elements with high strain energy and vice versa • To minimize compliance for given weight can use an optimality criterion method.

Ole Sigmund’s Site • http: //www. topopt. dtu. dk/ • Good summary and many examples • Minimize compliance for given volume • Provides also a 99 -line computer code that we will analyze. • Can get also a mobile phone ap that would do for you topology optimization.

Problem top • Use the top ap or the web site to design a bar in tension with aspect ratio of 3, with the tensile loads applied at two corners of the rectangle.