Topology Based Selection and Curation of Level Sets

Topology Based Selection and Curation of Level Sets Andrew Gillette Joint work with Chandrajit Bajaj and Samrat Goswami Center for Computational Visualization Institute of Computational and Engineering Sciences Department of Computer Sciences March 2007 University of Texas at Austin

Problem Statement Given a trivariate function we want to select a level set L(r) = with the following properties: 1) L(r) is a single, smooth component. 2) L(r) does not have any topological or geometrical features of size less than where the size of a feature is measured in the complementary space. The value of is determined by the application domain. Center for Computational Visualization University of Texas at Austin March 2007

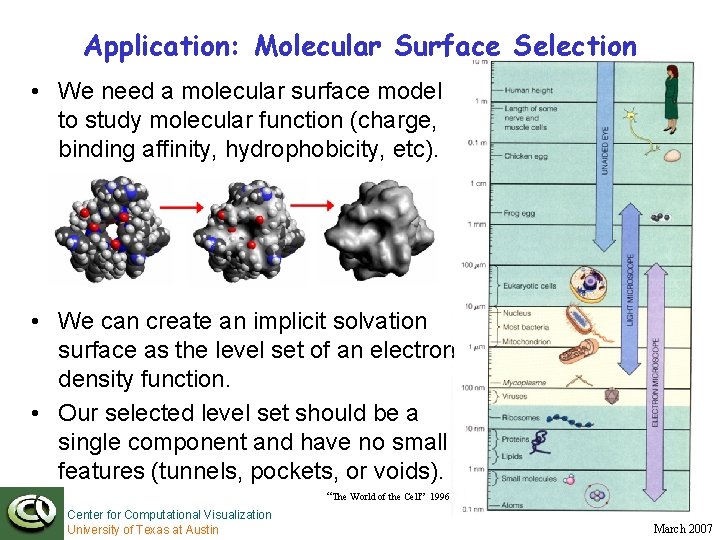
Application: Molecular Surface Selection • We need a molecular surface model to study molecular function (charge, binding affinity, hydrophobicity, etc). • We can create an implicit solvation surface as the level set of an electron density function. • Our selected level set should be a single component and have no small features (tunnels, pockets, or voids). “The World of the Cell” 1996 Center for Computational Visualization University of Texas at Austin March 2007

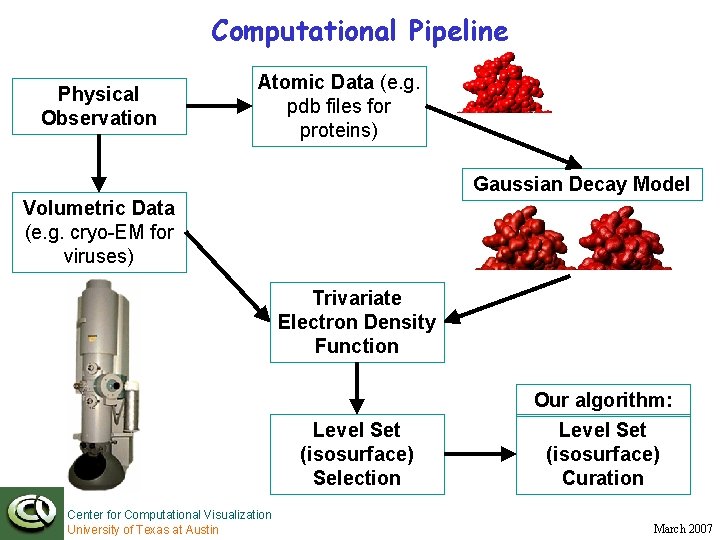
Computational Pipeline Physical Observation Atomic Data (e. g. pdb files for proteins) Gaussian Decay Model Volumetric Data (e. g. cryo-EM for viruses) Trivariate Electron Density Function Level Set (isosurface) Selection Center for Computational Visualization University of Texas at Austin Our algorithm: Level Set (isosurface) Curation March 2007

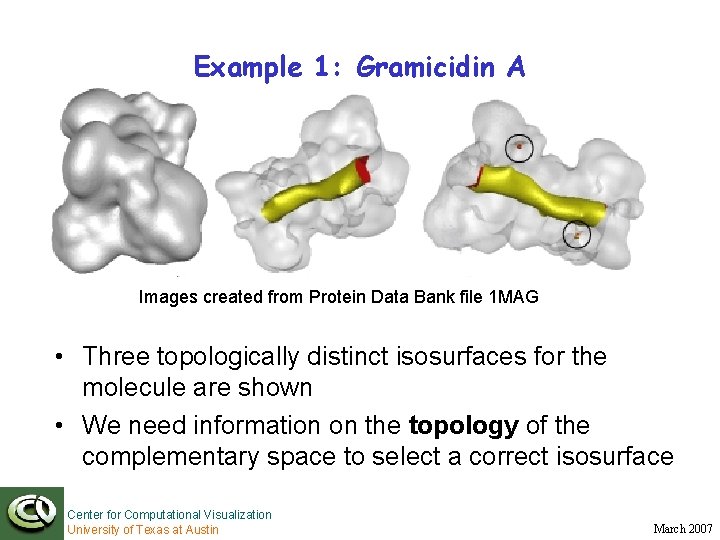
Example 1: Gramicidin A Images created from Protein Data Bank file 1 MAG • Three topologically distinct isosurfaces for the molecule are shown • We need information on the topology of the complementary space to select a correct isosurface Center for Computational Visualization University of Texas at Austin March 2007

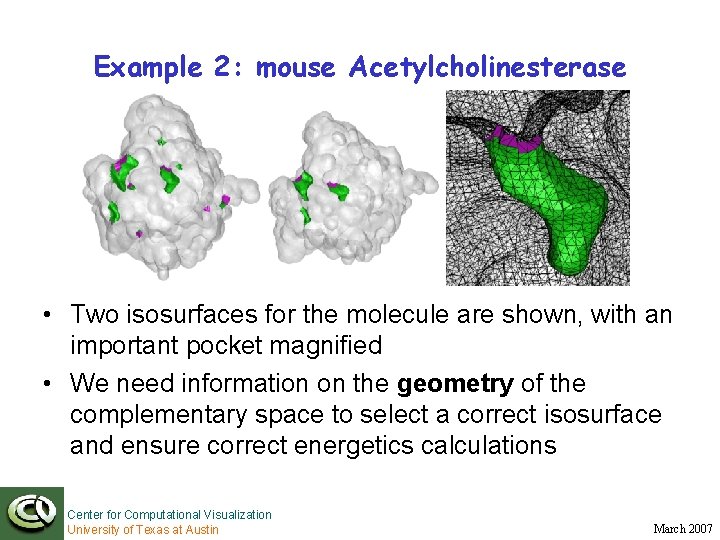
Example 2: mouse Acetylcholinesterase • Two isosurfaces for the molecule are shown, with an important pocket magnified • We need information on the geometry of the complementary space to select a correct isosurface and ensure correct energetics calculations Center for Computational Visualization University of Texas at Austin March 2007

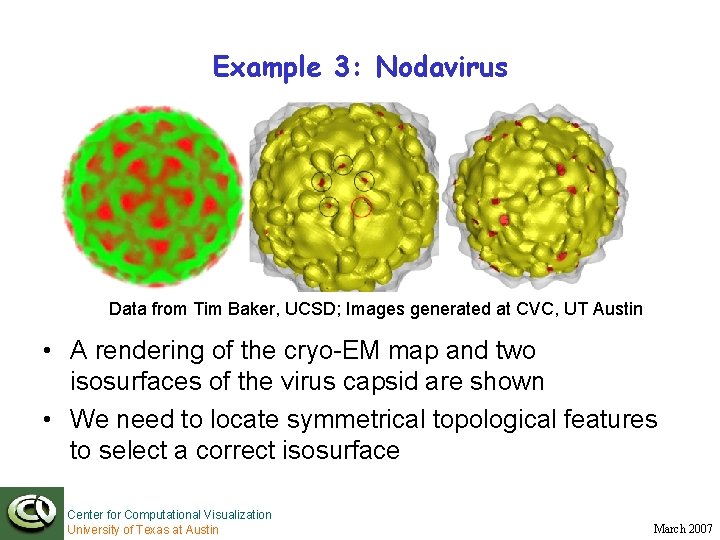
Example 3: Nodavirus Data from Tim Baker, UCSD; Images generated at CVC, UT Austin • A rendering of the cryo-EM map and two isosurfaces of the virus capsid are shown • We need to locate symmetrical topological features to select a correct isosurface Center for Computational Visualization University of Texas at Austin March 2007

Mathematical Preliminaries A. Contour Tree B. Voronoi / Delaunay Triangulation C. Distance Function and Stable Manifolds Center for Computational Visualization University of Texas at Austin March 2007

Prior Related Work Isosurface Selection via Contour Tree Modern application of contour trees: “Trekking in the alps without freezing or getting tired” (de Berg, van Kreveld: 1997) “Contour trees and small seed sets for isosurface traversal” (van Kreveld, van Oostrum, Bajaj, Pascucci, Schikore: 1997) Computation via split and join trees: “Computing contour trees in all dimensions” (Carr, Snoeyink, Axen: 2001) Betti numbers and augmented contour trees: “Parallel computation of the topology of level sets” (Pascucci, Cole-Mc. Laughlin: 2003) Distance Function and Stable Manifold Computation “Shape segmentation and matching with flow discretization” (Dey, Giesen, Goswami: 2003) “Surface reconstruction by wrapping finite point sets in space” (Edelsbrunner: 2002) “The flow complex: a data structure for geometric modeling. ” (Giesen, John: 2003) “Identifying flat and tubular regions of a shape by unstable manifolds” (Goswami, Dey, Bajaj: 2006) Center for Computational Visualization University of Texas at Austin March 2007

Level Sets and Contours • In this talk, f(x, y, z) will denote the electron density at the point (x, y, z) • An isosurface in this context is a level set of the function f, that is, a set of the type • Each component of an isosurface is called a contour • We select an isosurface with a single component via the contour tree Center for Computational Visualization University of Texas at Austin Isosurface with three contours March 2007

Contour Tree • Recall • A critical isovalue of f is a value r such that f -1(r) is not a 2 -manifold • Examples: r is a value where contours emerge, split, or vanish. r=1 r=2 r=3 non-critical Center for Computational Visualization University of Texas at Austin March 2007

Contour Tree • The contour tree is a tool used to aid in the selection of an isosurface • Vertices: subset of critical values of f • Edges: connect vertices along which a contour smoothly deforms Increasing isovalues Isovalue selector Center for Computational Visualization University of Texas at Austin March 2007

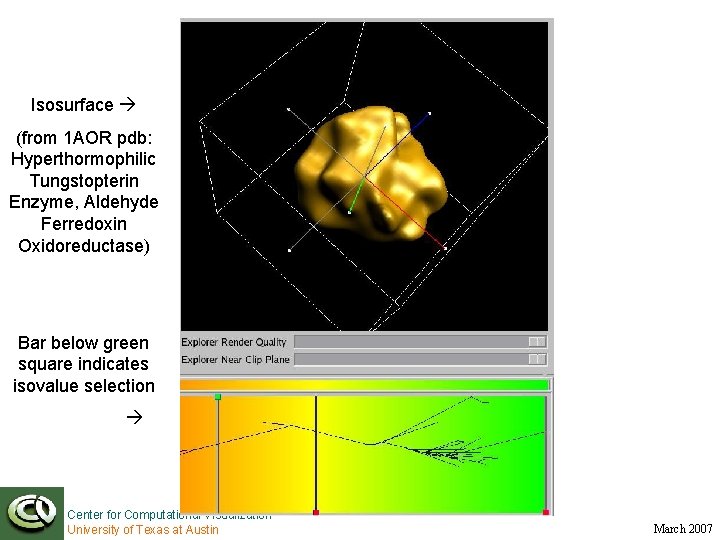
Isosurface (from 1 AOR pdb: Hyperthormophilic Tungstopterin Enzyme, Aldehyde Ferredoxin Oxidoreductase) Bar below green square indicates isovalue selection Center for Computational Visualization University of Texas at Austin March 2007

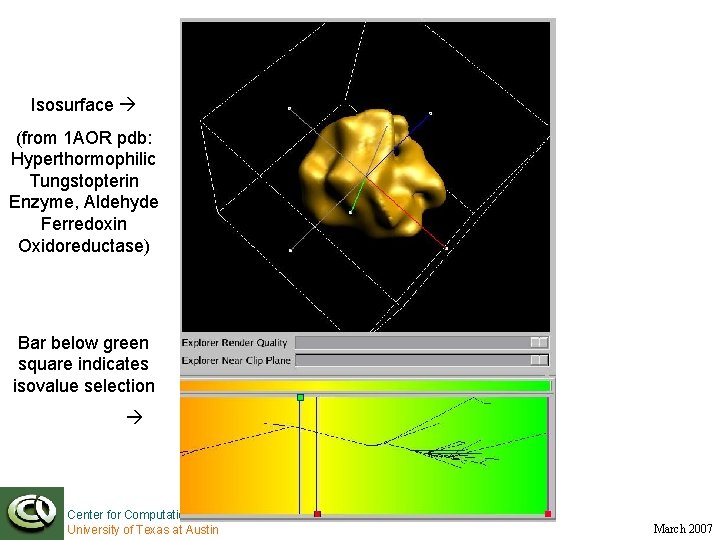
Isosurface (from 1 AOR pdb: Hyperthormophilic Tungstopterin Enzyme, Aldehyde Ferredoxin Oxidoreductase) Bar below green square indicates isovalue selection Center for Computational Visualization University of Texas at Austin March 2007

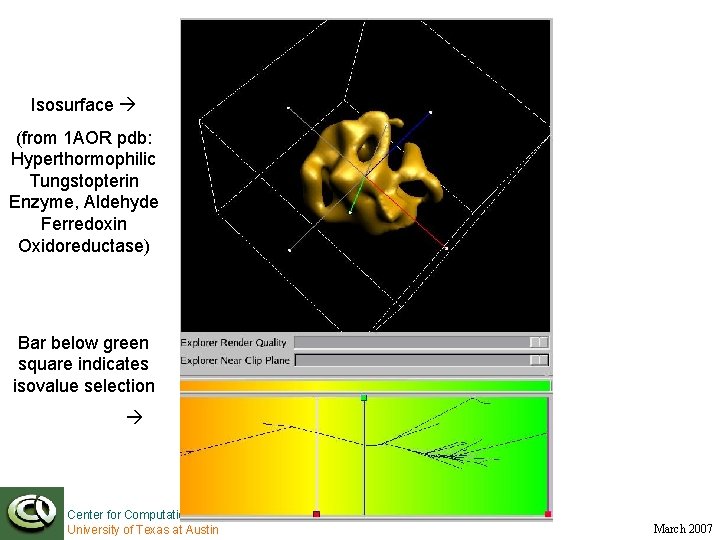
Isosurface (from 1 AOR pdb: Hyperthormophilic Tungstopterin Enzyme, Aldehyde Ferredoxin Oxidoreductase) Bar below green square indicates isovalue selection Center for Computational Visualization University of Texas at Austin March 2007

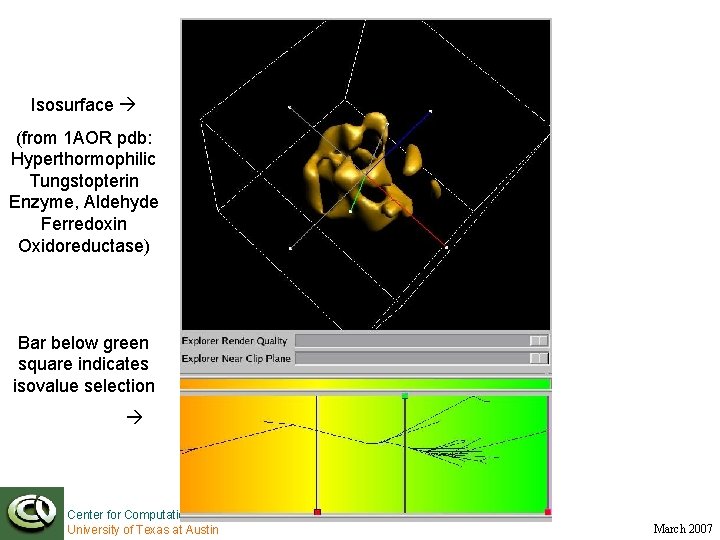
Isosurface (from 1 AOR pdb: Hyperthormophilic Tungstopterin Enzyme, Aldehyde Ferredoxin Oxidoreductase) Bar below green square indicates isovalue selection Center for Computational Visualization University of Texas at Austin March 2007

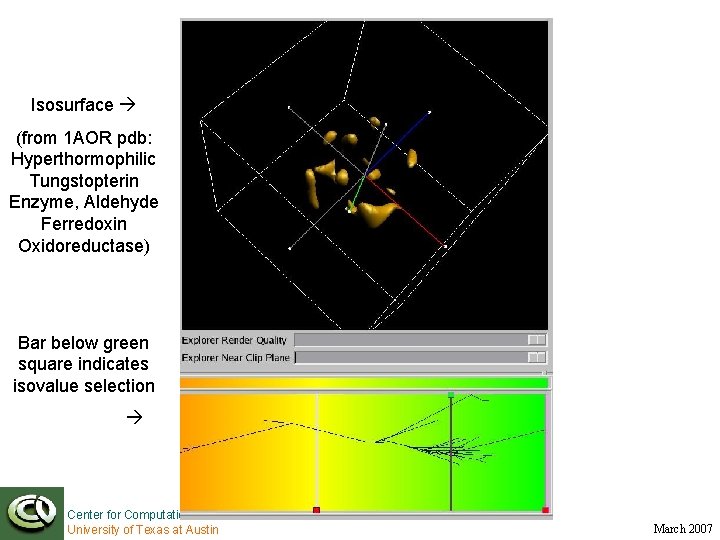
Isosurface (from 1 AOR pdb: Hyperthormophilic Tungstopterin Enzyme, Aldehyde Ferredoxin Oxidoreductase) Bar below green square indicates isovalue selection Center for Computational Visualization University of Texas at Austin March 2007

Voronoi Diagram • Let P be a finite set of points in • The set of Vp partition and “meet nicely” along faces and edges. • A 2 -D example is shown Center for Computational Visualization University of Texas at Austin March 2007

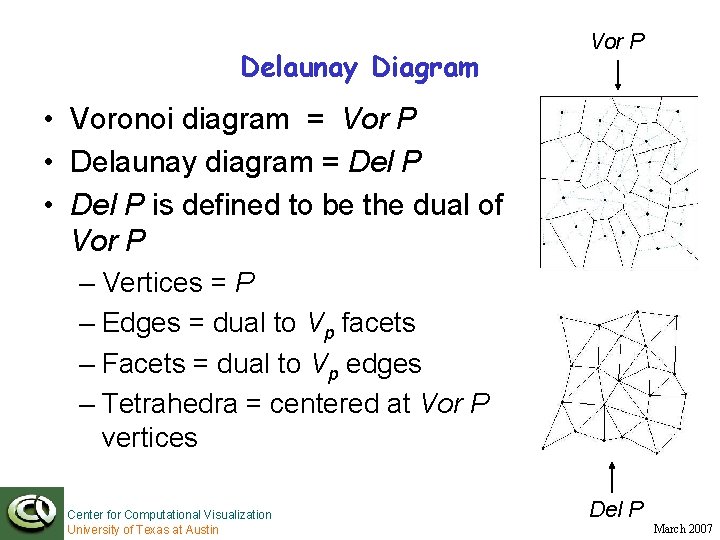
Delaunay Diagram Vor P • Voronoi diagram = Vor P • Delaunay diagram = Del P • Del P is defined to be the dual of Vor P – Vertices = P – Edges = dual to Vp facets – Facets = dual to Vp edges – Tetrahedra = centered at Vor P vertices Center for Computational Visualization University of Texas at Austin Del P March 2007

The distance function • Let S be a surface smoothly embedded in • Let P be a finite sampling of points on S. Then we approximate: Center for Computational Visualization University of Texas at Austin March 2007

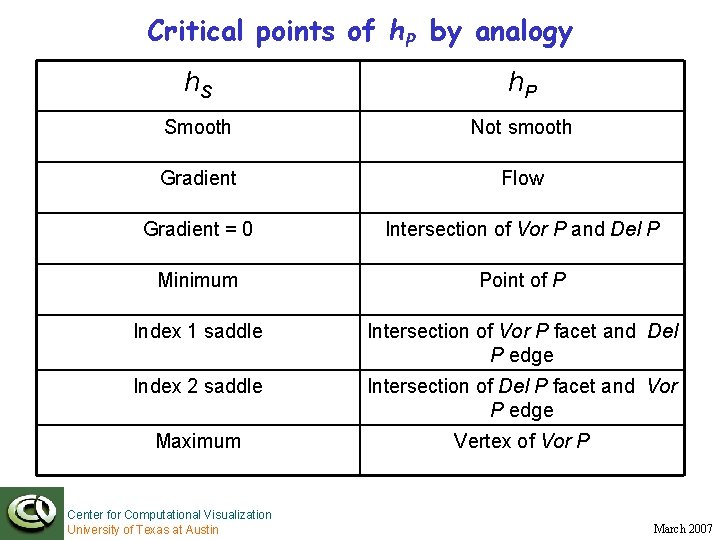
Critical points of h. P by analogy h. S h. P Smooth Not smooth Gradient Flow Gradient = 0 Intersection of Vor P and Del P Minimum Point of P Index 1 saddle Intersection of Vor P facet and Del P edge Index 2 saddle Intersection of Del P facet and Vor P edge Maximum Vertex of Vor P Center for Computational Visualization University of Texas at Austin March 2007

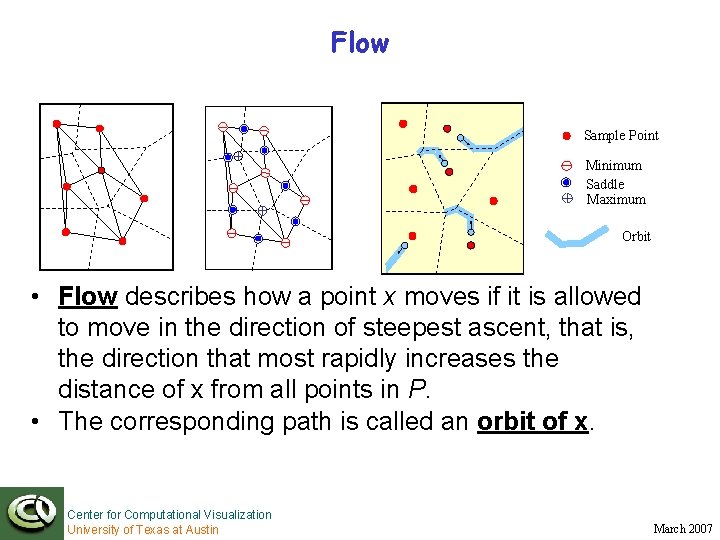
Flow Sample Point Minimum Saddle Maximum Orbit • Flow describes how a point x moves if it is allowed to move in the direction of steepest ascent, that is, the direction that most rapidly increases the distance of x from all points in P. • The corresponding path is called an orbit of x. Center for Computational Visualization University of Texas at Austin March 2007

Stable Manifolds Given a critical value c of h. P, the stable manifold of c is the set of points whose orbits end at c. Stable manifold of a… …has boundary S. M. of a… Max Index 2 saddle Index 1 saddle Min (no boundary) Center for Computational Visualization University of Texas at Austin March 2007

Algorithm and Results A. Description of Algorithm B. Results C. Future Work Center for Computational Visualization University of Texas at Austin March 2007

Algorithm in words Given an isosurface S sampled by pointset P: 1. Find critical points of distance function h. P 2. Classify critical points exterior to S as max, saddle, or saddle incident on infinity 3. Cluster points based on stable manifolds 4. Classify clusters based on number of mouths 5. Rank clusters based on geometric significance Center for Computational Visualization University of Texas at Austin March 2007

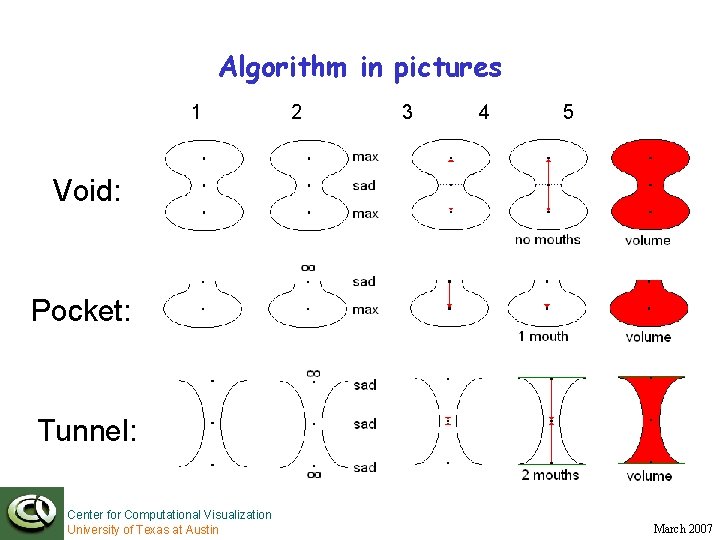
Algorithm in pictures 1 2 3 4 5 Void: Pocket: Tunnel: Center for Computational Visualization University of Texas at Austin March 2007

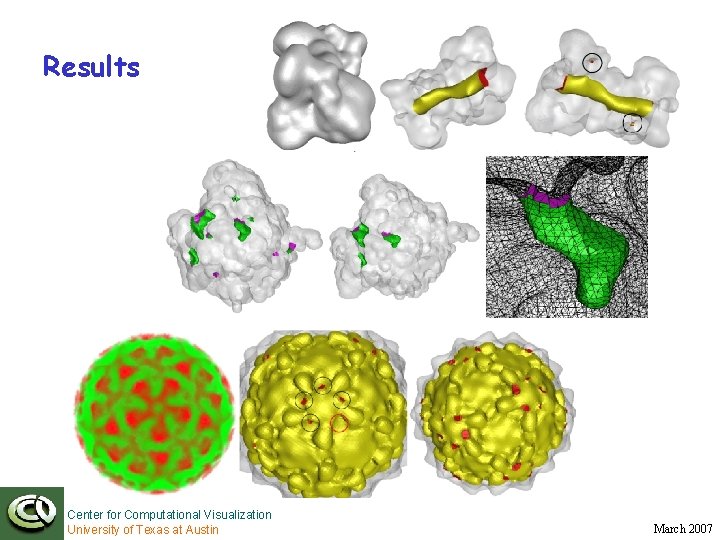
Results Center for Computational Visualization University of Texas at Austin March 2007

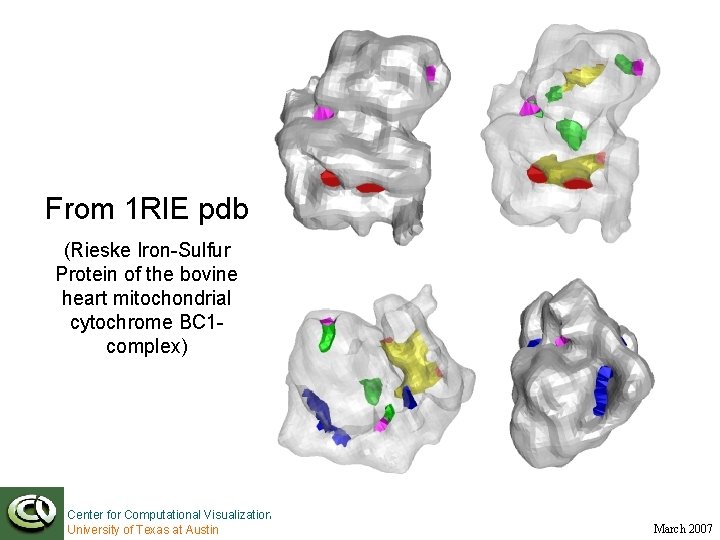
Results From 1 RIE pdb (Rieske Iron-Sulfur Protein of the bovine heart mitochondrial cytochrome BC 1 complex) Center for Computational Visualization University of Texas at Austin March 2007

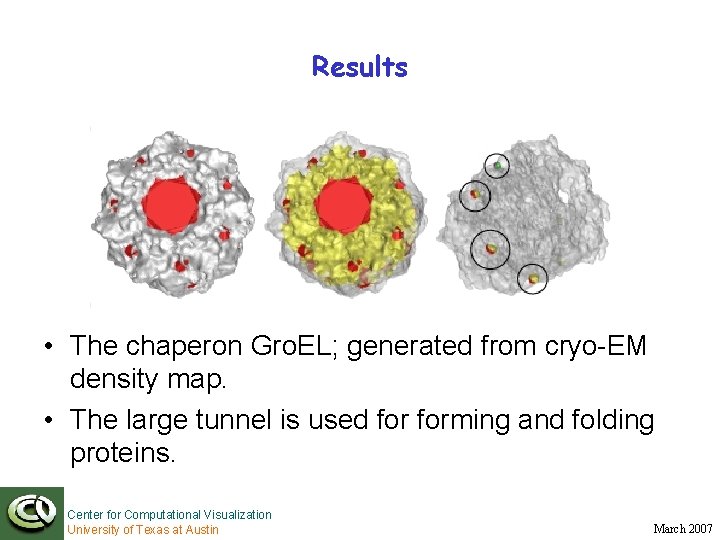
Results • The chaperon Gro. EL; generated from cryo-EM density map. • The large tunnel is used forming and folding proteins. Center for Computational Visualization University of Texas at Austin March 2007

Future Work Ø What makes a point set P sufficient for applying our algorithm? Ø How can we provide a “quick update” to the distance function for a range of isovalues? Ø Compare energy calculations on our pre- and post-curation surfaces. Center for Computational Visualization University of Texas at Austin March 2007

Thank you! (Danke) Center for Computational Visualization University of Texas at Austin March 2007