Topological reach of fieldtheoretical topological quantum computation Mario
































- Slides: 44

Topological reach of field-theoretical topological quantum computation Mario Rasetti Politecnico di Torino & ISI Foundation

Preliminaries n n The object: Construction of new efficient quantum algorithms for topological invariants The general context: Quantum Information Theory (Turing machine, circuit model, Lambda calculus, Post system and all that in quantum version …) in its Quantum Field Theory version n The results: Efficient quantum algorithms for any observable of Chern-Simons topological quantum field theory, in particular the Jones polynomial for knots in 3 and the invariants of 3 -manifolds

Scheme n n Part I n knot theory; n The Jones polynomial; n Computational complexity; n Quantum computation; Part II n The Jones polynomial in QFT; n Unitary representation of the braid group; n The quantum circuit;

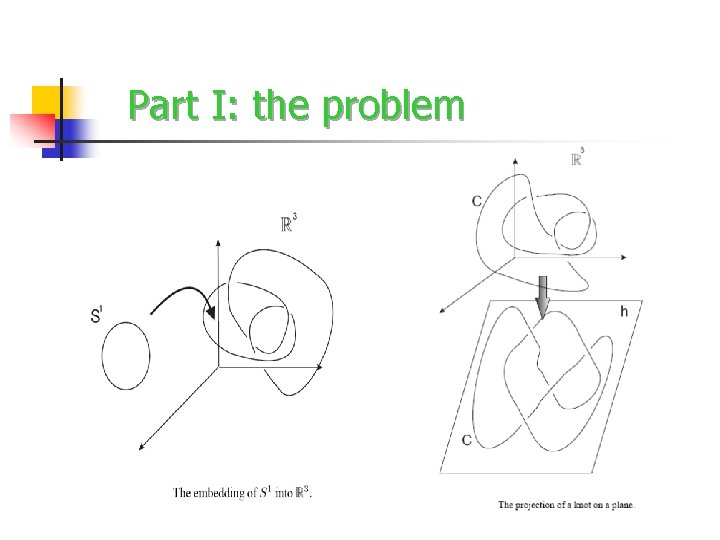
Part I: the problem Knot theory is the branch of topology concerning with the properties of knots. The most important problem in knot theory is the classification of knots: given two knots can we determine whether they are topologically equivalent or not?

Part I: the problem

Part I: the problem A knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode for some of the topological properties of a class of knots. The Jones polynomial is one of the most important such knot invariants

Part I: the problem Definition of the Jones polynomial by braid representation The original definition of the Jones polynomial results from: a trace of the braid group representation into the Temperley Lieb algebra

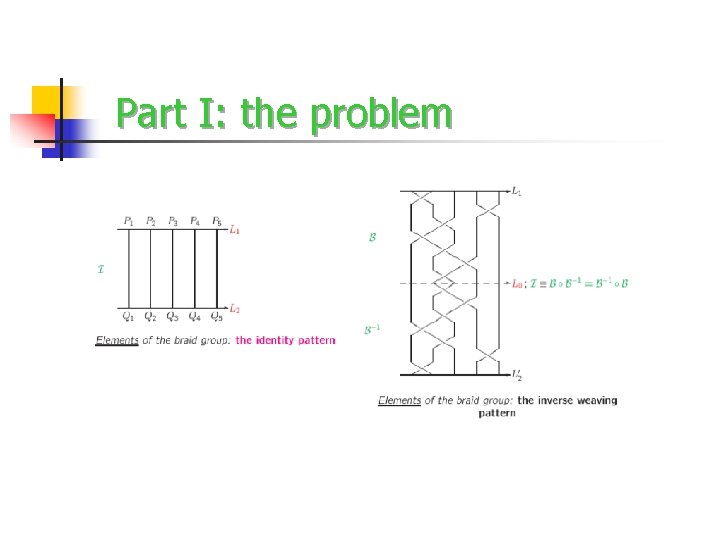
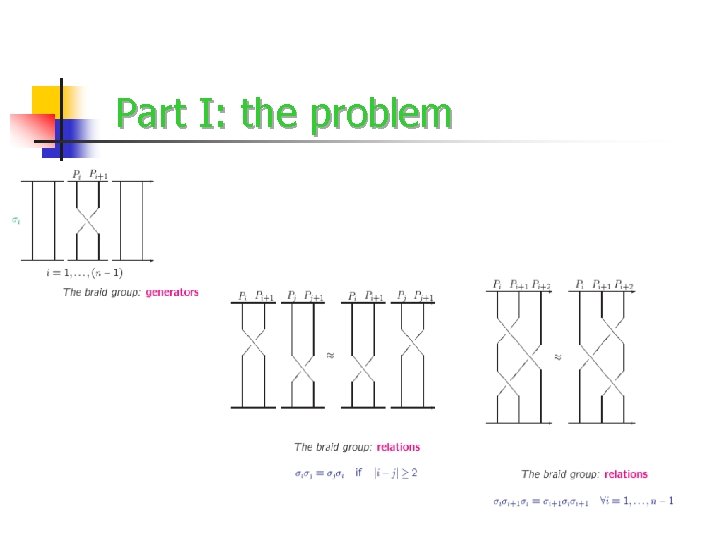
Part I: the problem The braid group on n strands is a group with an intuitive geometrical realization Presentation : for The Automaton based on the Spin Network Quantum Simulator accepts the Braid language

Part I: the problem

Part I: the problem

Part I: the problem

Part I: the problem The Temperley-Lieb algebra . . . .

Part I: the problem Knot-braid connection A given link L L L (coloured) can always be seen as the closure of a braid (Alexander theorem)

Part I: the problem Defining a representation with coefficients in such that and The Jones polynomial is given by V. F. R. Jones, A polynomial invariant for links via von Neumann algebras , Bull. Amer. Math. Soc. 129 (1985), 103 -112.

Part I: the problem § How hard is to evaluate the Jones polynomial from a computational point of view? § We know that there are no efficient classical algorithms for its evaluation: the Jones polynomial is a #P-hard problem § Can we provide an efficient quantum algorithm? Jaeger, Vertigan and Welsh, On the computational complexity of the Jones and Tutte Polynomials, Mathematical Proceedings of the Cambridge Phil. Soc. 108(1990), 35 -53

Part I: Computational Complexity q The Jones polynomial is #P-hard: hard means that all the problems in #P can be polynomially reduced to it. q From this it follows that, efficiently solving #P-hard problems we could even solve NP-complete problems, and so we could prove P=NP. . . too good to be true. . . That much for exact solutions, but what about approximate solutions?

Part I: Computational Complexity q Some #P-hard problems admit an efficient approximate solution q We showed that evaluation of the Jones polynomial can be done efficiently with a quantum computer if we search for an approximate solution q In fact the approximate evaluation of the Jones polynomial is the first known BQP-complete problem

Part II: the method Additive approximation n Let the quantum circuit constructed be of length O(poly(n)) acting on n qubits, and let be a pure state of n qubits which can be prepared in time O(poly(n)). It is then possible to sample in O(poly(n)) time from random variables X, Y in such a way that

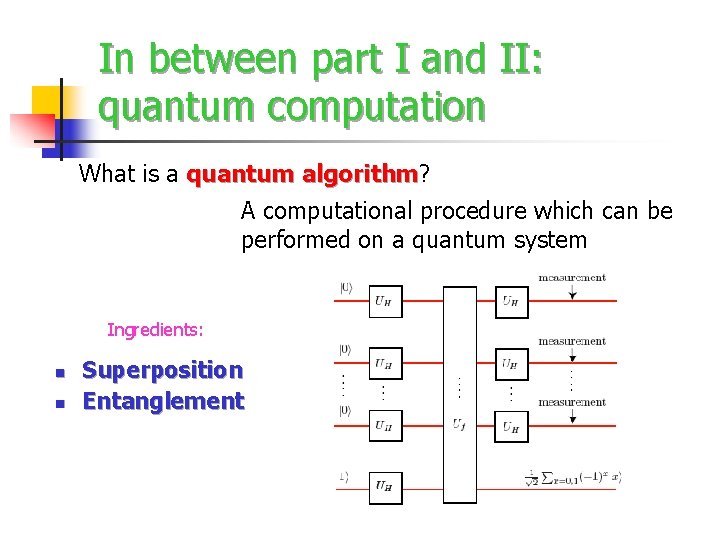
In between part I and II: quantum computation What is a quantum algorithm? algorithm A computational procedure which can be performed on a quantum system Ingredients: n n Superposition Entanglement

Quantum Computation Turing’s machine

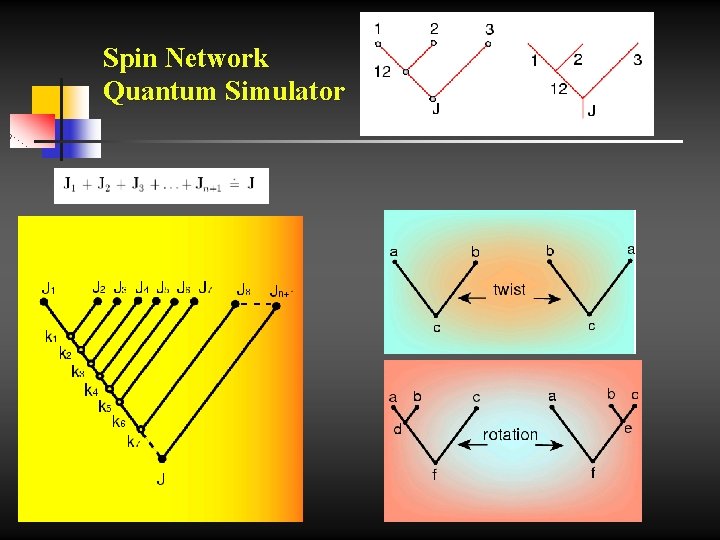
Spin Network Quantum Simulator The spin network simulator (SNQS) models bridge circuit schemes for standard quantum computation and notions from TQFTs. Its key tool is provided by the fiber space structure underlying the model, which exhibits combinatorial properties closely related to SU(2) state sum models. It can be thought of as non-Boolean version of the quantum circuit model, with unitary gates expressed in terms of: i) recoupling coefficients ( 3 nj symbols) between inequivalent binary ii) coupling schemes of N (n+1) SU(2)-angular momenta; iii)ii) Wigner rotations in the eigenspace of the total angular momentum.

Spin Network Quantum Simulator i) the combinatorial structure – induced by the SU(2) coalgebra – allows representing any computation process as a path over a graph, as in the classical case. The graph is the base space of a fiber bundle which sustains the simulator dynamics as well as information coding. ii) the extension to the quantum deformed algebra su(2)q iii) maps it to a quantum automaton structure; v) The 3 n-strand braid group acts on the functor: it is this vi) action that defines the evolution of the initial state.

Spin Network Quantum Simulator

Spin Network Quantum Simulator Hilbert spaces and Quantum Codes n (V, E) Alphabet and Words

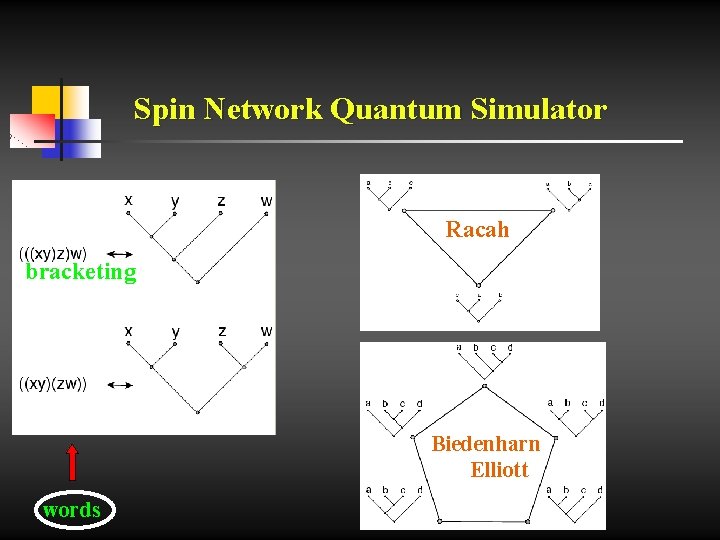
Spin Network Quantum Simulator Explicitly: where there appears the Racah -Wigner 6 j symbol of SU(2) and f plays the role of the total angular momentum quantum number. 6 j symbols satisfy consistency conditions given by: the Biedenharn-Elliot equalities the Racah identities and the orthogonality relations

Spin Network Quantum Simulator Racah bracketing Biedenharn Elliott words

Spin Network Quantum Simulator N. B. Mapping class group – Hatcher & Thurston

J 3( ) SNQS the graph 3 (V, E) The fiber space structure of the spin network simulator for (n+1) = 4 spins. Vertices and edges on the perimeter of the graph 3 (V, E) have to be identified through the antipodal map. The “blown up” vertex shows the local computational Hilbert space.

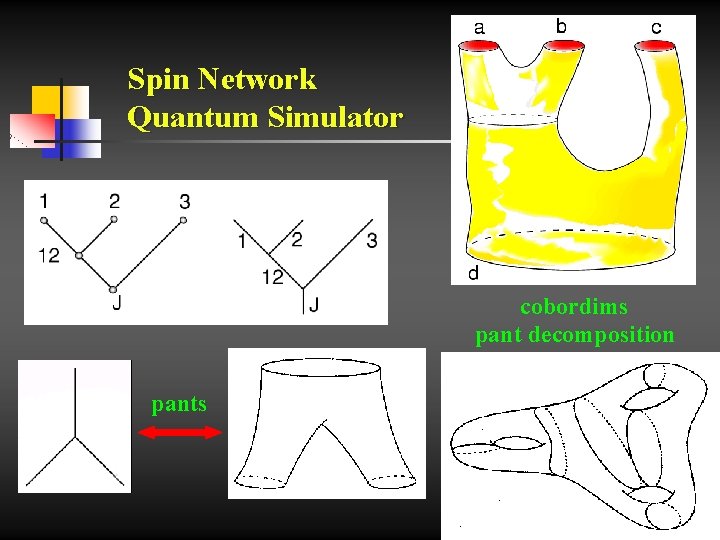
Spin Network Quantum Simulator cobordims pant decomposition pants

Spin Network Quantum Simulator

In between part I and II: quantum computation Approximate evaluation of the Jones polynomial is BQP-c v BQP=Bounded error Quantum Polynomial time: it is the class of decision problems solvable by a quantum computer in polynomial time with an error probability < ¼ v These are the problems which a quantum computer can “reasonably” solve v A BQP-complete problem is important to compare quantum computers and classical computers Bordewich, Freedman, Lovasz, Welsh, Approximate counting and quantum Computation, Comb. Probab. Comput. 14(2005), 737 -754

Part II: the method n n We use the realization of the Jones polynomial in quantum field theory, i. e. as the expectation value of observables in Chern-Simons Topological Quantum Field Theory (CS-TQFT) In CS-TQFT the Jones polynomial is the expectation value of Wilson loop operators

Part II: the method Chern-Simons TQFT Is a 3 -dimensional topological quantum field theory In TQFT the correlation functions do not depend on the metric of space-time and can be used to derive topological invariants k is a (integer) coupling parameter A is a connection one-form, valued in the Lie algebra of the group G (=SU(2)), the gauge group of theory M is a 3 -dimensional manifold E. Witten, Quantum field theory and the Jones polynomial, Comm. In Math. Phys. 121(1989), 351 -399

Part II: the method

Part II: the method Chern-Simons TQFT To solve theory it is important to use the connection between CS-TQFT and WZW-CFT WZW is constructed on a finite dimensional Hilbert space which is the space of conformal blocks

Part II: the method Chern-Simons TQFT The observables are called Wilson loop operators: ρ is an irreps of the gauge group G and C is a knot; T are the generators of SU(2) in representation ρ; A is a connection on the principal fibre bundle P(M, G) The expectation value of Wilson loop operators is a topological invariant of manifold M. In particular if G=SU(2) we have the Jones polynomial.

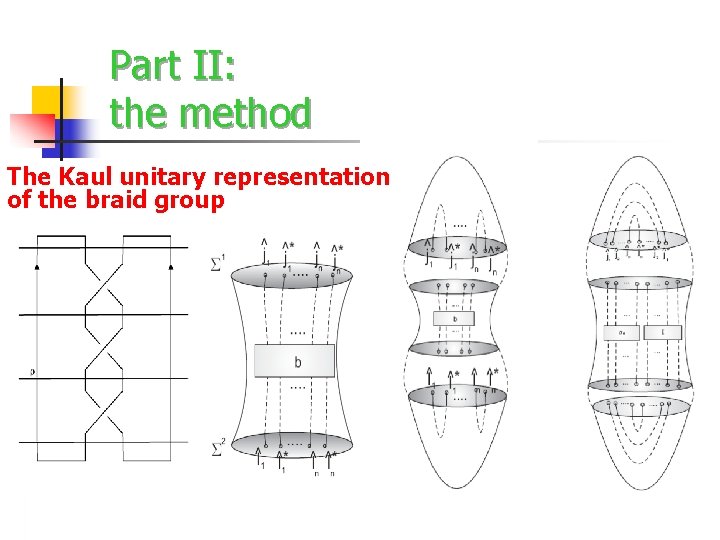
Part II: the method Quantum computing the Jones polynomial We use CS-TQFT exact solution, through a unitary representation of the braid group, to provide a quantum algorithm for the evaluation of the Jones polynomial Ø given a knot present it as a closure of a braid Ø cut the braid with horizontal lines in such a way that between two lines there is at most one crossing Ø use the unitary representation of the braid group to explicitly evaluate the topological invariant R. Kaul, Chern-Simons theory, colored-oriented braids and links invariants , Comm. In Math. Phys. 162(1994), 289

Part II: the method The Kaul unitary representation of the braid group

Part II: the method The Kaul unitary representation of the braid group The finite dimensional Hilbert space which we use to build the representation is the space of conformal blocks of WZW-CFT

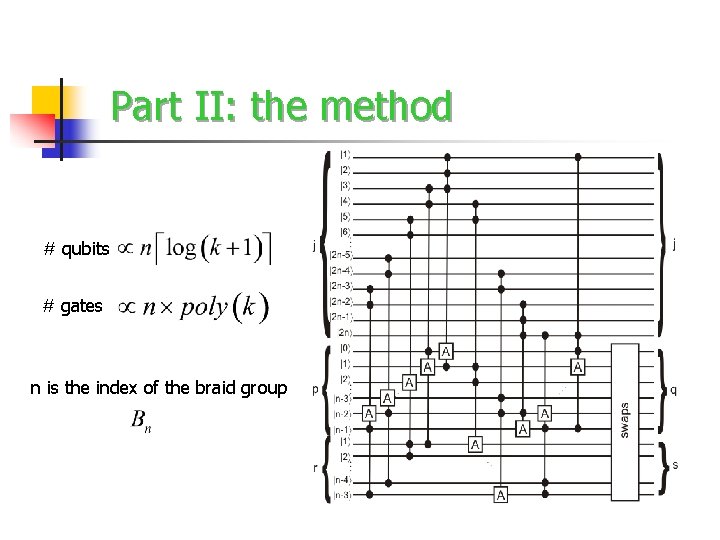
Part II: the method # qubits # gates n is the index of the braid group

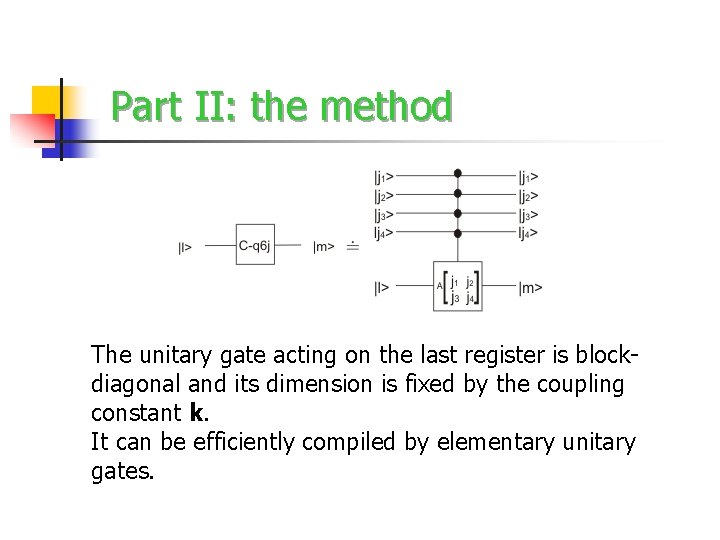
Part II: the method The unitary gate acting on the last register is blockdiagonal and its dimension is fixed by the coupling constant k. It can be efficiently compiled by elementary unitary gates.

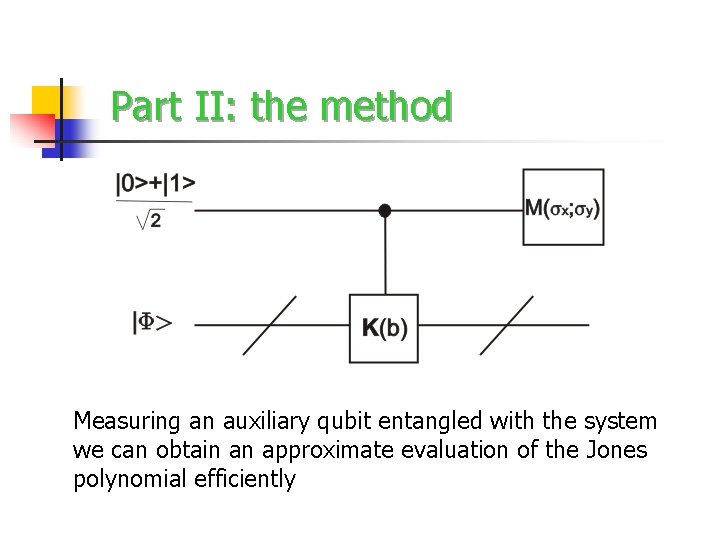
Part II: the method Measuring an auxiliary qubit entangled with the system we can obtain an approximate evaluation of the Jones polynomial efficiently

Results and discussion n n Efficient quantum algorithm for the approximation of the Jones polynomial It can be generalized to colored Jones polynomials It can be used to evaluate 3 -manifold invariants Links with theory of quantum automata in the framework of the q-deformed spin network simulator.

3 manifolds
 Quantum physics vs mechanics
Quantum physics vs mechanics Origin of quantum mechanics
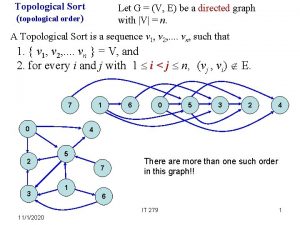
Origin of quantum mechanics Topological sort calculator
Topological sort calculator Topological sorting
Topological sorting Difference between selection sort and bubble sort
Difference between selection sort and bubble sort Topological sort uses
Topological sort uses Topological sort algorithm
Topological sort algorithm Topological sort pseudocode
Topological sort pseudocode Topological sort calculator
Topological sort calculator White path theorem
White path theorem Topological sort can be implemented by?
Topological sort can be implemented by? Topological mott insulator
Topological mott insulator Topological sort kahn's algorithm
Topological sort kahn's algorithm Topological sort
Topological sort Topological sort
Topological sort Mpp algorithm in image processing
Mpp algorithm in image processing Topological band theory
Topological band theory Graph topological sort
Graph topological sort Topological sort online
Topological sort online Unique topological ordering
Unique topological ordering Partial order relation
Partial order relation Topological sort bfs
Topological sort bfs Representation and description in digital image processing
Representation and description in digital image processing Topological sort codeforces
Topological sort codeforces Topological sort strongly connected components
Topological sort strongly connected components Self adjusting computation
Self adjusting computation Data cube computation
Data cube computation Fertilizer computation philrice
Fertilizer computation philrice Two round multiparty computation via multi-key fhe
Two round multiparty computation via multi-key fhe Introduction to the theory of computation
Introduction to the theory of computation Theory of computation
Theory of computation The theory of computation
The theory of computation Pagerank computation
Pagerank computation Pagerank
Pagerank Medication calculation formula
Medication calculation formula How to calculate drop rate of iv fluid
How to calculate drop rate of iv fluid Mineral fertilizer
Mineral fertilizer Income tax computation format
Income tax computation format Expanded withholding tax computation
Expanded withholding tax computation Anbn pda
Anbn pda Ambiguity
Ambiguity Media computation
Media computation Kjeldahl method formula derivation
Kjeldahl method formula derivation Types of languages in theory of computation
Types of languages in theory of computation Tzu chieh wei
Tzu chieh wei