Topics Paths and Circuits 11 2 A C

Topics • Paths and Circuits (11. 2) A C E B F D G 1

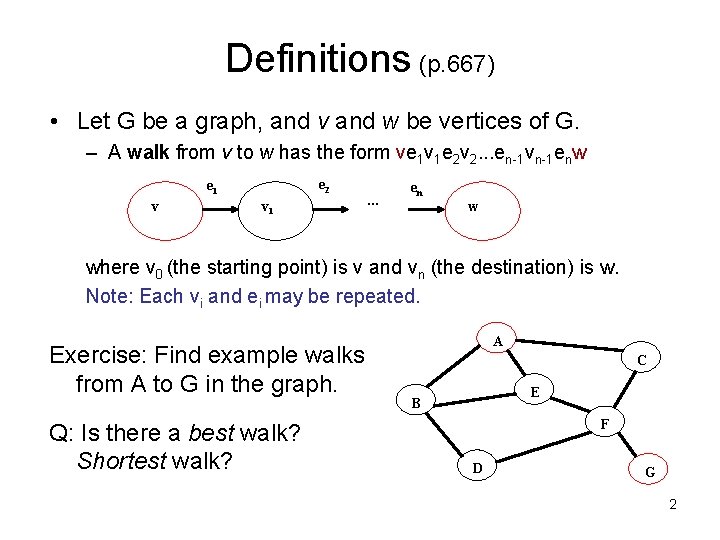
Definitions (p. 667) • Let G be a graph, and v and w be vertices of G. – A walk from v to w has the form ve 1 v 1 e 2 v 2. . . en-1 vn-1 enw e 2 e 1 v v 1 … en w where v 0 (the starting point) is v and vn (the destination) is w. Note: Each vi and ei may be repeated. Exercise: Find example walks from A to G in the graph. Q: Is there a best walk? Shortest walk? A C E B F D G 2

Why are we concerned with walks in a graph? • Many real-world applications … – Navigation – Transportation – Computer networks Network topology Routing of data packets Wireless network (node movement) … – Problem solving, games, gambling, … – Searching (e. g. , searching the Internet) – Communication – Management – … 3

Why are we concerned with walks in a graph? See http: //en. wikipedia. org/wiki/Graph_theory#Applications • “Applications of graph theory are primarily, but not exclusively, concerned with labeled graphs and various specializations of these. • Structures that can be represented as graphs are ubiquitous, and many problems of practical interest can be represented by graphs. • The link structure of a website could be represented by a directed graph: the vertices are the web pages available at the website and a directed edge from page A to page B exists if and only if A contains a link to B. • A similar approach can be taken to problems in travel, biology, computer chip design, and many other fields. • The development of algorithms to handle graphs is therefore of major interest in computer science. ” 4

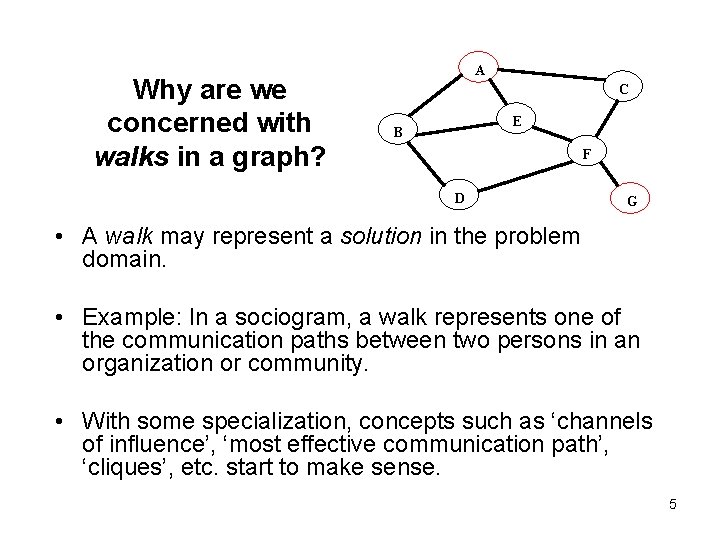
Why are we concerned with walks in a graph? A C E B F D G • A walk may represent a solution in the problem domain. • Example: In a sociogram, a walk represents one of the communication paths between two persons in an organization or community. • With some specialization, concepts such as ‘channels of influence’, ‘most effective communication path’, ‘cliques’, etc. start to make sense. 5

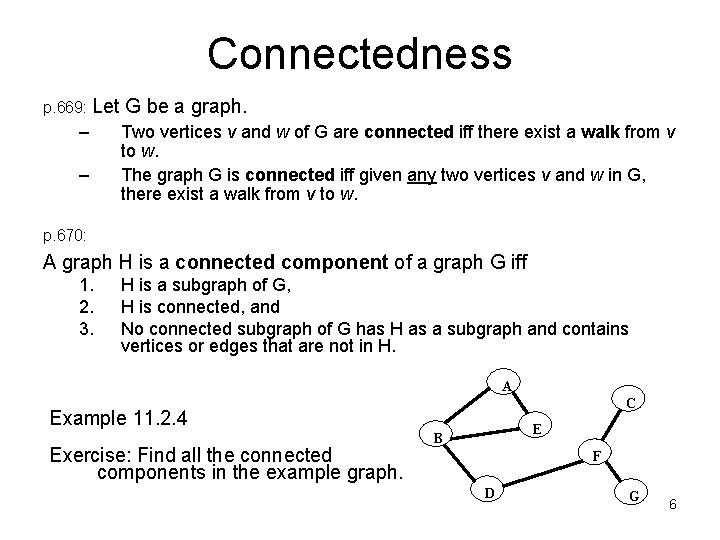
Connectedness p. 669: Let – – G be a graph. Two vertices v and w of G are connected iff there exist a walk from v to w. The graph G is connected iff given any two vertices v and w in G, there exist a walk from v to w. p. 670: A graph H is a connected component of a graph G iff 1. 2. 3. H is a subgraph of G, H is connected, and No connected subgraph of G has H as a subgraph and contains vertices or edges that are not in H. A C Example 11. 2. 4 Exercise: Find all the connected components in the example graph. E B F D G 6

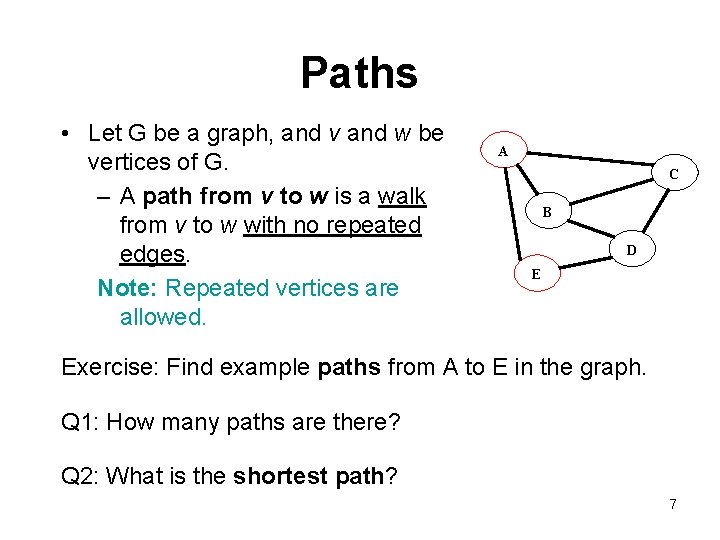
Paths • Let G be a graph, and v and w be vertices of G. – A path from v to w is a walk from v to w with no repeated edges. Note: Repeated vertices are allowed. A C B D E Exercise: Find example paths from A to E in the graph. Q 1: How many paths are there? Q 2: What is the shortest path? 7

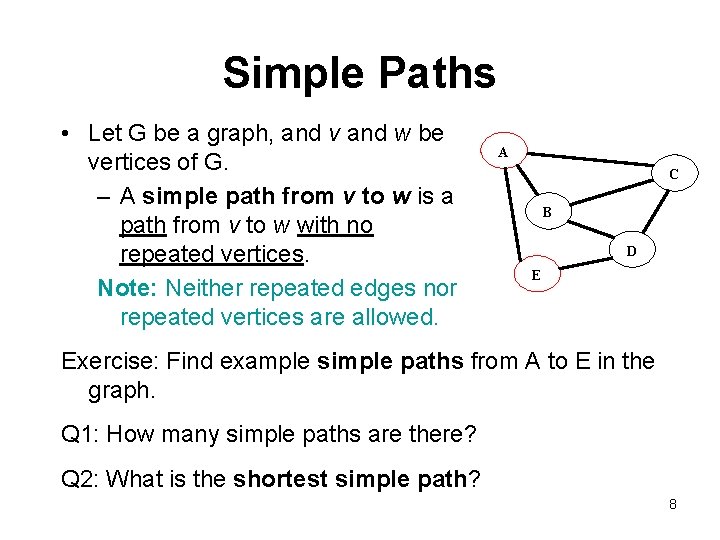
Simple Paths • Let G be a graph, and v and w be vertices of G. – A simple path from v to w is a path from v to w with no repeated vertices. Note: Neither repeated edges nor repeated vertices are allowed. A C B D E Exercise: Find example simple paths from A to E in the graph. Q 1: How many simple paths are there? Q 2: What is the shortest simple path? 8

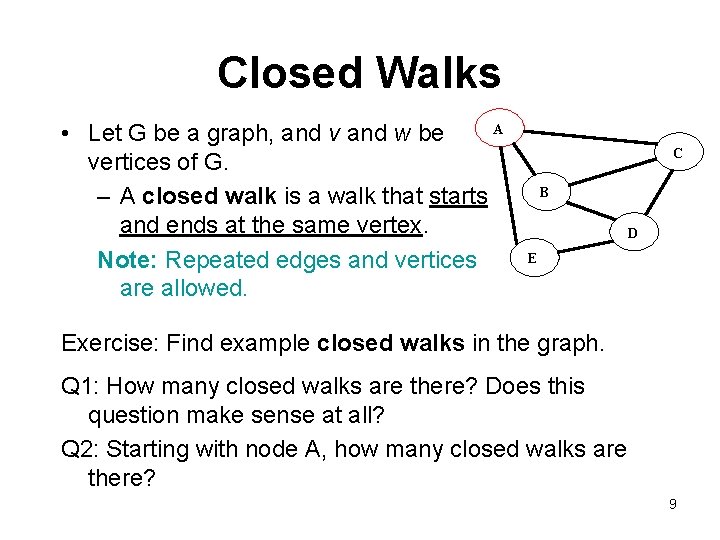
Closed Walks A • Let G be a graph, and v and w be vertices of G. – A closed walk is a walk that starts and ends at the same vertex. Note: Repeated edges and vertices are allowed. C B D E Exercise: Find example closed walks in the graph. Q 1: How many closed walks are there? Does this question make sense at all? Q 2: Starting with node A, how many closed walks are there? 9

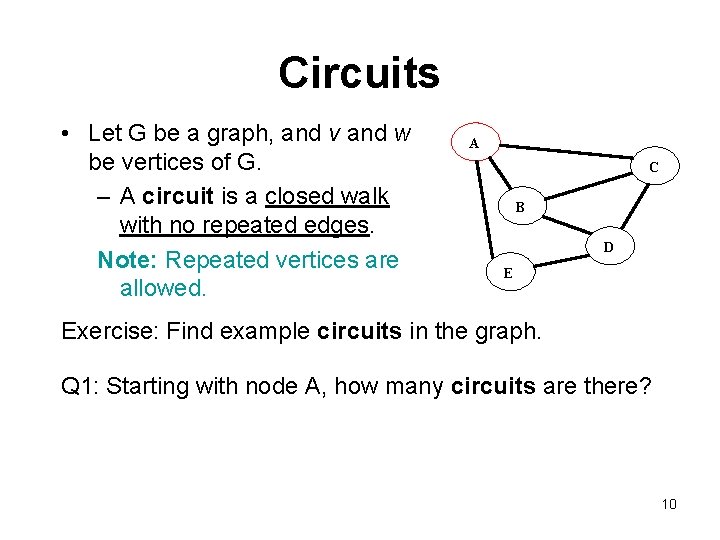
Circuits • Let G be a graph, and v and w be vertices of G. – A circuit is a closed walk with no repeated edges. Note: Repeated vertices are allowed. A C B D E Exercise: Find example circuits in the graph. Q 1: Starting with node A, how many circuits are there? 10

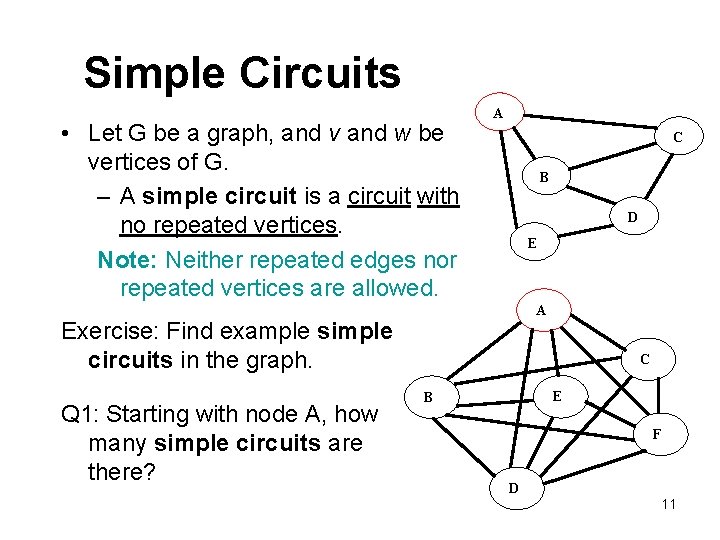
Simple Circuits • Let G be a graph, and v and w be vertices of G. – A simple circuit is a circuit with no repeated vertices. Note: Neither repeated edges nor repeated vertices are allowed. A C B D E A Exercise: Find example simple circuits in the graph. Q 1: Starting with node A, how many simple circuits are there? C E B F D 11

Comparisons • • • p. 667: Table of comparisons Q: What’s the difference between a walk and a path? How about a walk and a closed walk? How about a path and a circuit? How about a path and a simple path? • How about a circuit and a simple circuit? • How about a simple path and a simple circuit? A C E B F D 12

Questions? 13

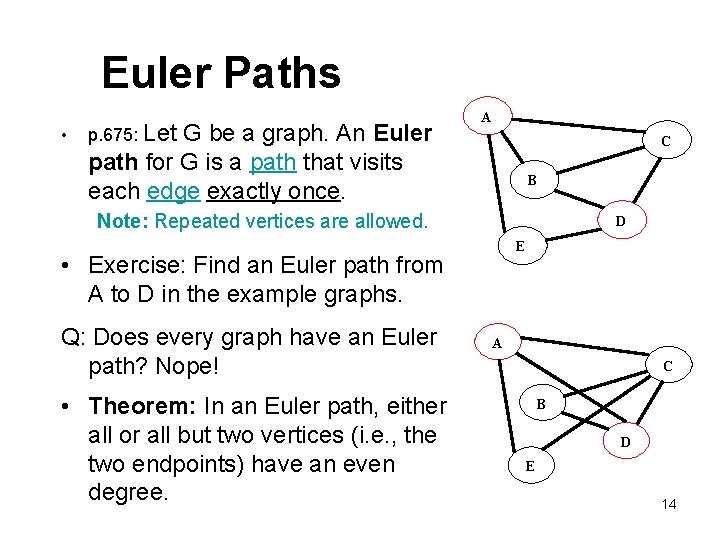
Euler Paths • p. 675: Let G be a graph. An Euler path for G is a path that visits each edge exactly once. A C B Note: Repeated vertices are allowed. D E • Exercise: Find an Euler path from A to D in the example graphs. Q: Does every graph have an Euler path? Nope! • Theorem: In an Euler path, either all or all but two vertices (i. e. , the two endpoints) have an even degree. A C B D E 14

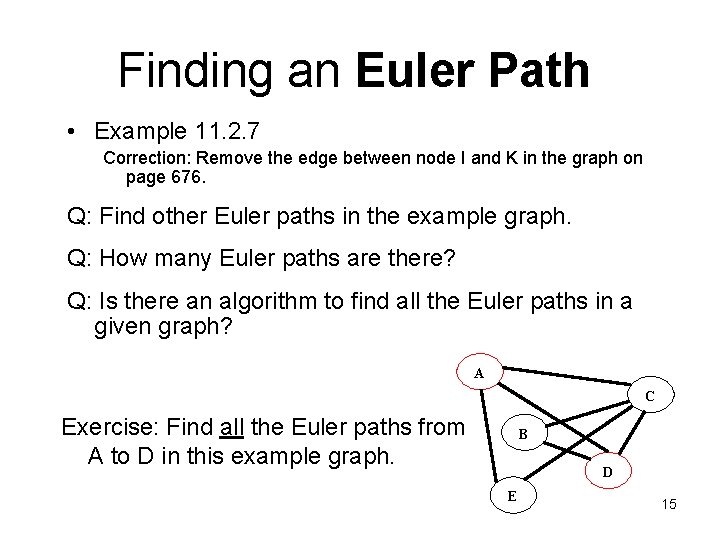
Finding an Euler Path • Example 11. 2. 7 Correction: Remove the edge between node I and K in the graph on page 676. Q: Find other Euler paths in the example graph. Q: How many Euler paths are there? Q: Is there an algorithm to find all the Euler paths in a given graph? A C Exercise: Find all the Euler paths from A to D in this example graph. B D E 15

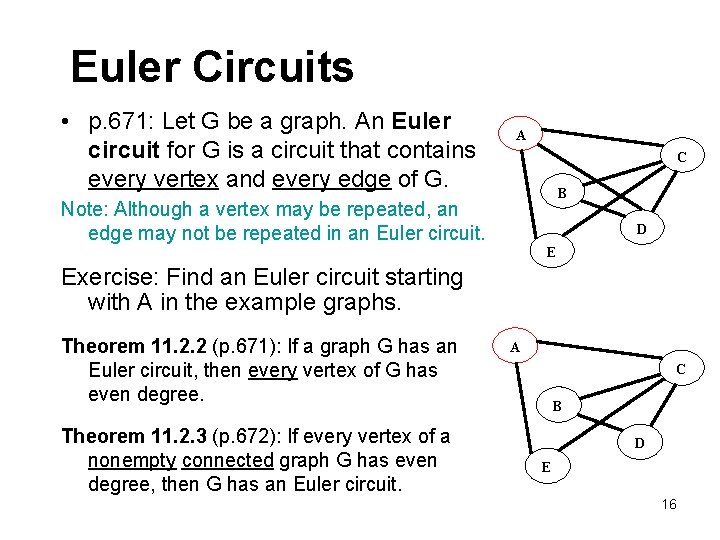
Euler Circuits • p. 671: Let G be a graph. An Euler circuit for G is a circuit that contains every vertex and every edge of G. A C B Note: Although a vertex may be repeated, an edge may not be repeated in an Euler circuit. D E Exercise: Find an Euler circuit starting with A in the example graphs. Theorem 11. 2. 2 (p. 671): If a graph G has an Euler circuit, then every vertex of G has even degree. Theorem 11. 2. 3 (p. 672): If every vertex of a nonempty connected graph G has even degree, then G has an Euler circuit. A C B D E 16

Questions? 17