Topics Inferential Statistics Inference Terminology Central Limit Theorem

Topics: Inferential Statistics • • Inference Terminology Central Limit Theorem Estimation – Point Estimation – Confidence Intervals • Hypothesis Testing

Inferential Statistics • Research is about trying to make valid inferences • Inferential statistics: the part of statistics that allows researchers to generalize their findings beyond data collected. • Statistical inference: a procedure for making inferences or generalizations about a larger population from a sample of that population

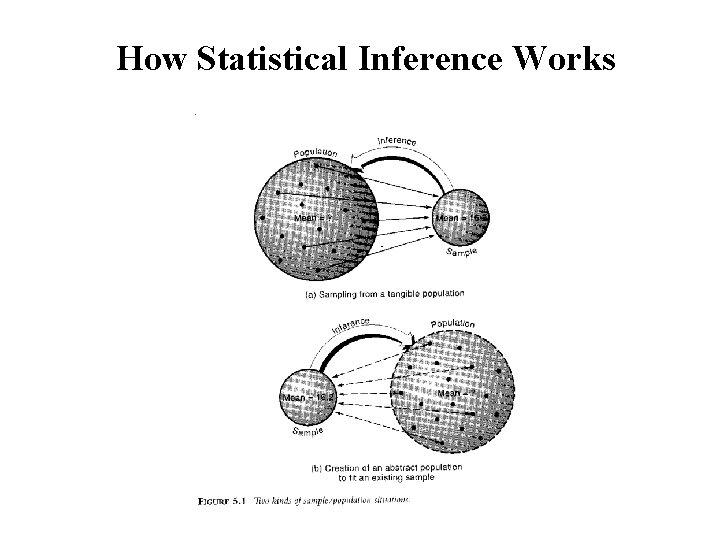
How Statistical Inference Works

Basic Terminology • Population: any collection of entities that have at least one characteristic in common • Parameter: the numbers that describe characteristics of scores in the population (mean, variance, s. d. , etc. )

Basic Terminology (cont’d) • Sample: a part of the population • Statistic: the numbers that describe characteristics of scores in the sample (mean, variance, s. d. , correlation coefficient, reliability coefficient, etc. )

Basic Statistical Symbols

Basic Terminology (con’t) • Estimate: a number computed by using the data collected from a sample • Estimator: formula used to compute an estimate

The Process of Estimation

Types of Samples • Probability – – Simple Random Samples Simple Stratified Samples Systematic Samples Cluster Samples • Non Probability – – Purposive Samples Convenience Samples Quota Samples Snowball Samples

Limits on Inferences and Warnings • • Response Rates Source of data Sample size and sample quality “Random”

Estimation • Point Estimation • Interval estimation – Sampling Error – Sampling Distribution – Confidence Intervals

Interval Estimation • Interval Estimation: an inferential statistical procedure used to estimate population parameters from sample data through the building of confidence intervals • Confidence Intervals: a range of values computed from sample data that has a known probability of capturing some population parameter of interest

Sampling Error • Samples rarely mirror exactly the population • The sample statistics will almost always contain sampling error • The magnitude of the difference of the sampling statistic from the population parameter

Sampling Distribution • Sampling Distribution: a theoretical distribution that shows the frequency of occurrence of values of some statistic computed for all possible samples of size N drawn from some population. • Sampling Distribution of the Mean: A theoretical distribution of the frequency of occurrence of values of the mean computed for all possible samples of size N from a population

Sampling Distribution of Mean

Sampling Distribution of Means and Standard Error of the Means -3 sem -2 sem -1 sem u mu Population mean +1 sem +2 sem +3 sem

Central Limit Theorem • The sampling distribution of means, for samples of 30 or more: – Is normally distributed (regardless of the shape of the population from which the samples were drawn) – Has a mean equal to the population mean, “mu” regardless of the shape population or of the size of the sample – Has a standard deviation--the standard error of the mean--equal to the population standard deviation divided by the square root of the sample size

Sampling Distribution of 1000 Sample Means Ave minus 4. 5 pts Ave minus 3. 0 pts Ave minus 1. 5 pts Ave. IQ of 5000 4 th graders also Ave. of 1000 sample averages Ave. plus 1. 5 pts Ave. plus 3. 0 pts Ave. plus 4. 5 pts

Confidence Intervals • A defined interval of values that includes the statistic of interest, by adding and subtracting a specific amount from the computed statistic • A CI is the probability that the interval computed from the sample data includes the population parameter of interest

Factors Affecting Confidence Intervals

Various Levels of Confidence • When population standard deviation is known use Z table values: – For 95%CI: mean +/- 1. 96 s. e. of mean – For 99% CI: mean +/- 2. 58 s. e. of mean • When population standard deviation is not known use “Critical Value of t” table – For 95%CI: mean +/- 2. 04 s. e. of mean – For 99% CI: mean +/- 2. 75 s. e. of mean

95%Confidence Interval 95 times out of 100 the interval constructed around the sample mean will capture the population mean. 5 times out of 100 the interval will not capture the population mean 95% -2. 58 sem -1. 96 sem u mu +1. 96 sem +2. 58 sem

99%Confidence Interval 99 times out of 100 the interval constructed around the sample mean will capture the population mean. 1 time out of 100 the interval will not capture the population mean 99% -2. 58 sem u mu +2. 58 sem

Effects of Sample Size

Process for Constructing Confidence Intervals • Compute the sample statistic (e. g. a mean) • Compute the standard error of the mean • Make a decision about level of confidence that is desired (usually 95% or 99%) • Find tabled value for 95% or 99% confidence interval • Multiply standard error of the mean by the tabled value • Form interval by adding and subtracting calculated value to and from the mean