Topics in Cryptography Lecture 6 Topic Chosen Ciphertext

Topics in Cryptography Lecture 6 Topic: Chosen Ciphertext Security Lecturer: Moni Naor

Recap: chosen ciphertext security • Why chosen ciphertext/malleability matters • Taxonomy of Attacks and Security • Ideas for achieving CCA – Redundancy + Verification • The NIZK approach • Simple scheme achieving CCA 1 – Based on DDH – Modification achieving CCA 2 • Chosen-Ciphertext Security via Correlated Products

Homework: One time Signature Schemes • Show that if g is a one-way function the scheme is indeed a one-time signature scheme. • Show to obtain a strongly unforgeable signature scheme – You may use the existence of Universal One-way Hash Functions • Why do we need strongly unforgeable signature schemes in the CCA 2 scheme?

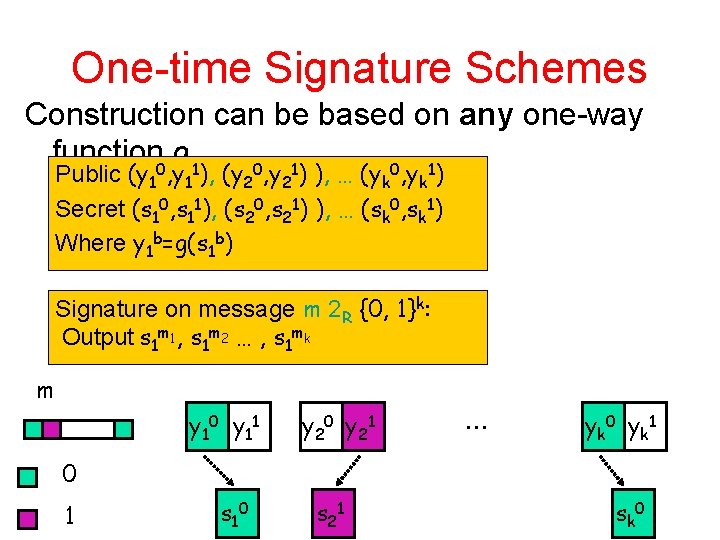
One-time Signature Schemes A signature scheme that is • Existentially unforgeable • Adversary A gets to pick and see signature on one message A Wins if he can find any other (message, signature) that is accepted by signature verification algorithm – Message should be different – Strongly unforgeable: also cannot find another signature to a message that has been signed

One-time Signature Schemes Construction can be based on any one-way function 0 g 1 0 1 Public (y 1 , y 1 ), (y 2 , y 2 ) ), … (yk , yk ) Secret (s 10, s 11), (s 20, s 21) ), … (sk 0, sk 1) Where y 1 b=g(s 1 b) Signature on message m 2 R {0, 1}k: Output s 1 m 1, s 1 m 2 … , s 1 mk m y 10 y 11 y 20 y 21 … y k 0 y k 1 0 1 s 10 s 21 s k 0

Universal One-Way Hash functions UOWHFs • A family of functions G={g|g: {0, 1}n → {0, 1}h(n)} Such that • Easy to sample g from G and g G has succinct description • Given (n, g, x) easy to compute g(x) • h(n) < n • Hard to find target collisions: – Given (n, g, x) hard to find x’ {0, 1}n where x ≠ x’ but g(x)=g(x’) Adversary picks x before

Homework: One time Signature Schemes • Show that if g is a one-way function the scheme is indeed a one-time signature scheme. • Show to obtain a strongly unforgeable signature scheme – You may use the existence of Universal One-way Hash Functions • Why do we need strongly unforgeable signature schemes in the CCA 2 scheme?

Motivation for Zero-knowledge Can turn any protocol that: • works well when the parties are benign (but curious) into • one that works well when the parties are malicious Usage of NIZK to obtain CCA is an exampel of the principle

Correlated Products • For a collection F of one-way functions consider (f 1(x 1), . . . , fk(xk)) for every f 1, . . . , fk ∈F. • f 1, . . . , fk is hard to invert for random (x 1, … , x k) • But what happens when x 1, … , xk are Repetition correlated?

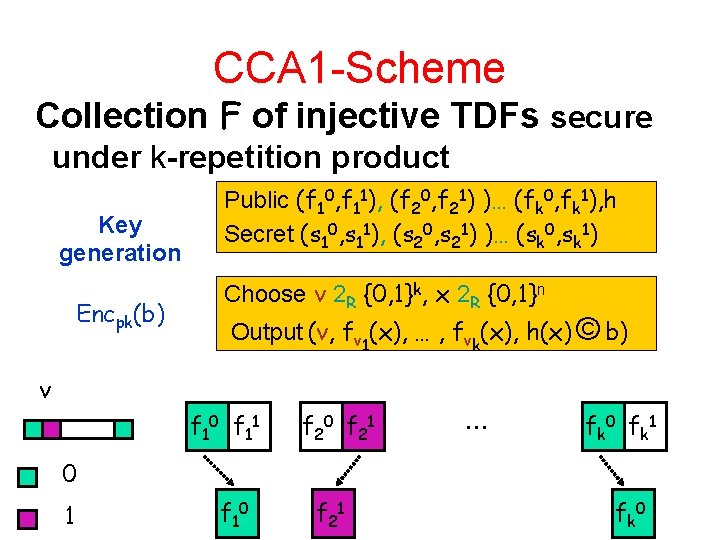
CCA-Security from Repetition Collection F of injective TDFs secure under k-repetition product • Hard-core bit h for F – Given f(x) infeasible to guess h(x) with a noticeable advantage Goldreich-Levin (inner product) is still hard core

CCA 1 -Scheme Collection F of injective TDFs secure under k-repetition product Key generation Encpk(b) Public (f 10, f 11), (f 20, f 21) )… (fk 0, fk 1), h Secret (s 10, s 11), (s 20, s 21) )… (sk 0, sk 1) Choose v 2 R {0, 1}k, x 2 R {0, 1}n Output (v, fv 1(x), … , fvk(x), h(x) © b) v f 10 f 11 f 20 f 21 … f k 0 f k 1 0 1 f 10 f 21 f k 0

Construction of Correlation Product Lossy Trapdoor Functions [Peikert Waters ’ 08] • Two indistinguishable collections: – F 0 collection of many-to-one functions – F 1 F collection of injective functions F 1 f 2 F 1 Indistinguishability f Hardness of inversion -1 f 2 F 0 0 Large indegree

Construction of Correlation Product Lossy Trapdoor Functions [Peikert Waters ’ 08] • Two indistinguishable collections: – F 0 collection of many-to-one functions – F 1 collection of injective functions • Various number-theoretic assumptions [PW ’ 08, GRS ’ 08, BFO ’ 08, . . . ] Claim: F 1 is secure under x 1 = … = xk – f is many-to-one: f(x) “reveals” only r ≪ n bits of x – f 1(x), … , fk(x) is one-way as long as r・k = n− (log n)

Realizing Lossy Trapdoors from DDH: (g, gx, gy, gxy) (g, gx, gy, gz) El Gamal: public key hg, h=gxi secret key x gxr+m Encrypt (small m): random r send (gr, hr gm ) Homomorphism on message and randomness Coordinate wise

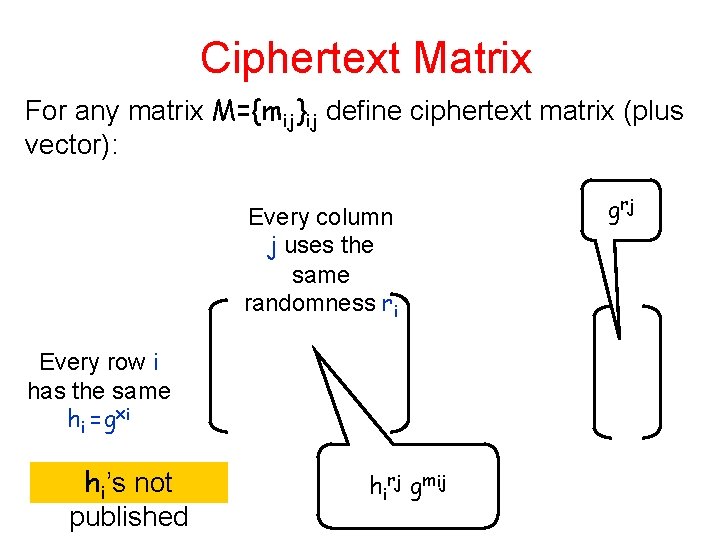
Ciphertext Matrix For any matrix M={mij}ij define ciphertext matrix (plus vector): Every column j uses the same randomness ri Every row i has the same hi =gxi hi’s not published hirj gmij g rj

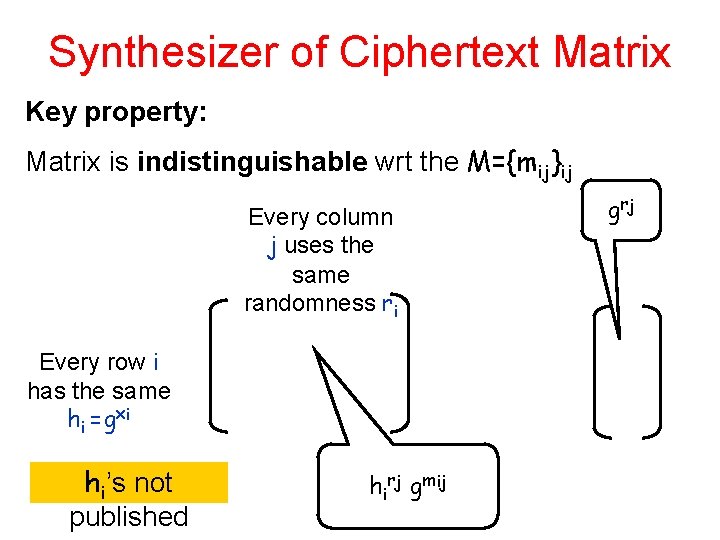
Synthesizer of Ciphertext Matrix Key property: Matrix is indistinguishable wrt the M={mij}ij Every column j uses the same randomness ri Every row i has the same hi =gxi hi’s not published hirj gmij g rj

Homework: getting rid of the one time Signature Schemes • Prove that for any two matrices M 0 and M 1 the resulting ciphertext matrix plus randomness vector are indistinguishable

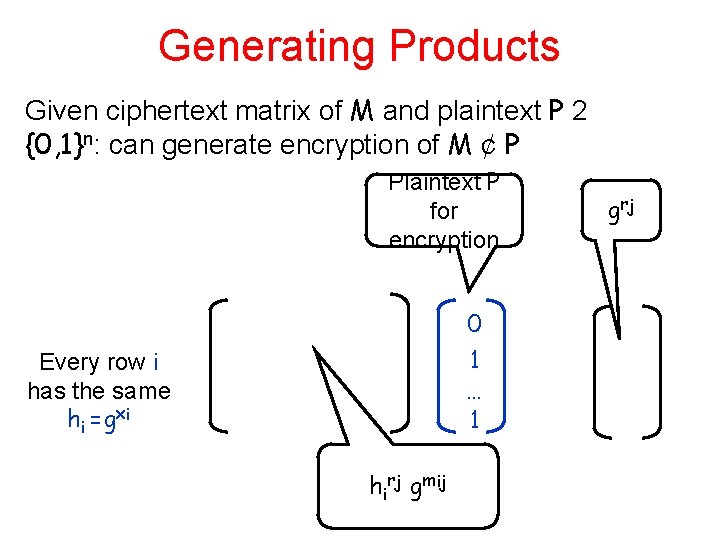
Generating Products Given ciphertext matrix of M and plaintext P 2 {0, 1}n: can generate encryption of M ¢ P Plaintext P for encryption 0 1 … 1 Every row i has the same hi =gxi hirj gmij g rj

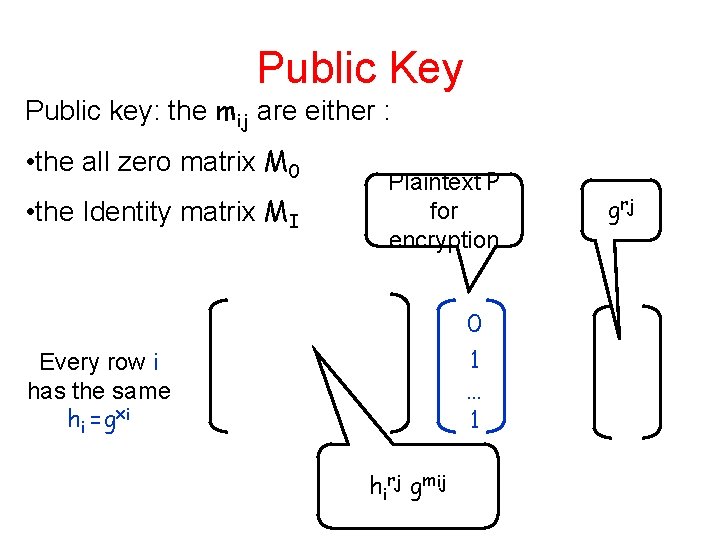
Public Key Public key: the mij are either : • the all zero matrix M 0 • the Identity matrix MI Plaintext P for encryption 0 1 … 1 Every row i has the same hi =gxi hirj gmij g rj

• Claim: if matrix is Identity: can reconstruct plaintext – From M ¢ P • Claim if matrix is all zero: lossy when dimension n larger than log q – Each entry: just a sum of the rj‘s according to P – Rest determined by hi – log q bits of information

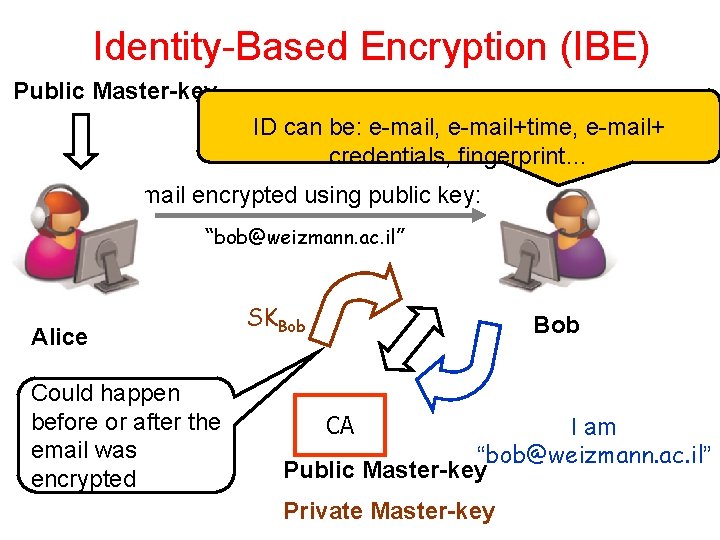
Identity Base Encryption (IBE) A public-key* encryption system where any arbitrary string can be used as the public key – Examples: user’s e-mail address, currentdate, biometric data… An authority publishes public Master-key Keeps secret private master key Extract: Given any string ID∈{0, 1}* can create SKID To encrypt need public-key and ID

Identity-Based Encryption (IBE) Public Master-key ID can be: e-mail, e-mail+time, e-mail+ credentials, fingerprint… email encrypted using public key: “bob@weizmann. ac. il” Alice Could happen before or after the email was encrypted SKBob CA I am “bob@weizmann. ac. il” Public Master-key Private Master-key

History • The concept was formulated by Adi Shamir in 1984 • First IBE schemes in 2001 – Boneh and Franklin - Crypto 2001 • Based on Pairing – Cocks – Intern. Conf. on Cryptography and Coding 2001 • Based on quadratic residuousity – First proposals: need random oracle – Later ones: standard model

Security Definition for IBE Semantic security against an adaptive id extraction – No polynomially bound adversary can distinguish with non neligible advantage between Target id encryptions of m 0 and m 1 under key id – m 0 and m 1 chosen by adversary – Adversary gets to issue extract requests • given idi obtain SKidi – How is id chosen: • Adaptively • Ahead of time: Selective-ID security – Extract may not be issued on target id

Getting CCA 1 from IBE • Public key: master public key of the IBE scheme, • Secret key: corresponding master secret key. • To encrypt a message m: – Generate a random string vk – Encrypts the message m with respect to the ``identity" vk. – Resulting ciphertext C – The ciphertext: h. C, vki.

CCA from IBE • Public key: master public key of the IBE scheme, • Secret key: corresponding master secret key. • To encrypt a message m: – Generate a key-pair (vk; sk) for a onetime strong signature scheme – Encrypt the message m with respect to the ``identity" vk. – Resulting ciphertext C is then signed using sk to obtain a signature . – The ciphertext: h. C, vk, i. • To decrypt a ciphertext h. C, vk, i: – Verify the signature on C using vk – If pass: extract the corresponding key to vk and

Getting rid of the one-time signatures One time signature: long and not so efficient • • Idea: replace signature with MACS – unconditional authentication – Replace the signature key with a commitment to the (MAC) hash function Pairwise ind • To encrypt a message m: – Generate (h, ck, dk) - ck commitment to h and dk decommitment. – Encrypt the message m ° dk ° h with respect to the identity ck. – Resulting ciphertext C is then authenticated using h: = h(C) – The ciphertext: h. C, ck, i. • To decrypt a ciphertext h. C, ck, i: – extract the corresponding key to ck and decrypt C to obtain m ° dk ° h

Homework: getting rid of the one time Signature Schemes • Is it possible to use commitment instead of one -time signature in the correlated products?

Is it circular? The value of h is still protected – from semantic security. Only know at one point all other points are unifomly ditributed For a challenge ciphertext h. C, ck, i • Any decryption C ’≠ Cquery with ck’≠ ck is “useless” – Can be answered by IBE query • If ck’ = ck query can guess whp that either – dk is not proper – h(C’) ≠ ’ - from the pairwise independence

Interactive Authentication P wants to convince V that he is approving message m P has a public key KP of an encryption scheme E. To authenticate a message m: • V P: Choose r 2 R {0, 1}n. Send c=E(m ° r, KP) • P V: Receiving c Decrypt c using KS Verify that prefix of plaintext is m. If yes - send r. V is satisfied if he receives the same r he choose

Is it Safe? Want: Existential unforgeability against adaptive chosen message attack – Adversary can ask to authenticate any sequence m 1, m 2, … – Has to succeed in making V accept a message m not authenticated – Has complete control over the channels • Intuition of security: if E does not leak information about plaintext – Nothing is leaked about r • Several problems: if E is “just” semantically secure against chosen plaintext attacks: – Adversary might change c=E(m ° r, KP) into c’=E(m’ ° r, KP) • Malleability

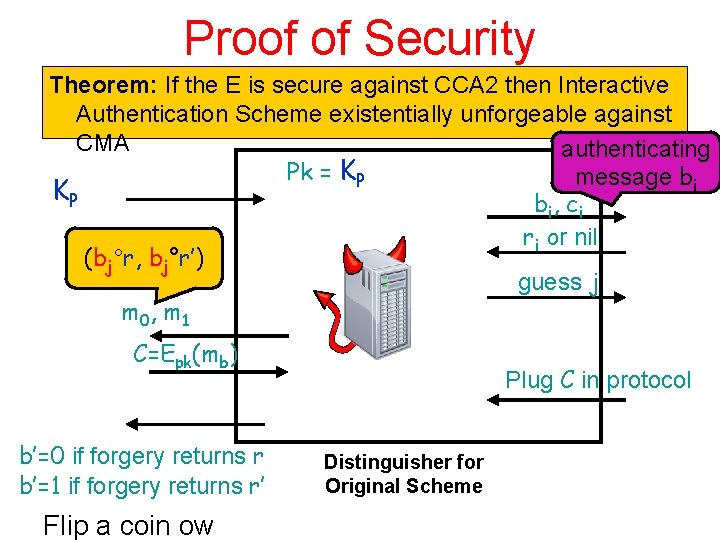
Interactive Authentication P wants to convince V that he is approving message m P has a public key KP of an encryption scheme E. To authenticate a message m: • V P: Choose r 2 R {0, 1}n. Send c=E(m ° r, KP) • P V : Receiving c Decrypt c using KS Verify that prefix of plaintext is m. If yes - send r. V is satisfied if he receives the same r he chose Claim: if E is CCA 2 secure, then scheme is existentially unforgeable against active adversary

Proof of Security Theorem: If the E is secure against CCA 2 then Interactive Authentication Scheme existentially unforgeable against CMA authenticating Pk = KP message bi KP b i, c i ri or nil (bj°r, bj°r’) guess j m 0, m 1 C=Epk(mb) b’=0 if forgery returns r b’=1 if forgery returns r’ Flip a coin ow Plug C in protocol Distinguisher for Original Scheme

No receipts • Can the verifier convince third party that the prover approved a certain message?

Authentication and Non. Repudiation • Key idea of modern cryptography [Diffie. Hellman]: can make authentication (signatures) transferable to third party - Non-repudiation. – Essential to contract signing, e-commerce… • Digital Signatures: last 25 years major effort in – Research • Notions of security • Computationally efficient constructions – Technology, Infrastructure (PKI), Commerce,

Is non-repudiation always desirable? Not necessarily so: • Privacy of conversation, no (verifiable) record. – Do you want everything you ever said to be held against you? • If Bob pays for the authentication, shouldn't be able to transfer it for free • Perhaps can gain efficiency Alternative: (Plausible) Deniability If the recipient (or any recipient) could have generated the conversation himself or an indistinguishable one

Deniable Authentication Setting: • Sender has a public key known to receiver • Want to an authentication scheme such that the receiver keeps no receipt of conversation. This means: • Any receiver could have generated the conversation itself. – There is a simulator that for any message m and verifier V* generates an indistinguishable conversation. – Exactly as in Zero-Knowledge! – An example where zero-knowledge is the ends, not the means!

Ring Signatures and Authentication Can we keep the sender anonymous? Idea: prove that the signer is a member of an ad hoc set – Other members do not cooperate – Use their `regular’ public-keys • Encryption – Should be indistinguishable which member of the set is actually doing the authentication Ring Signatures: Rivest, Shamir and Tauman Bob Alice? Eve

A Public Key Authentication Protocol P has a public key PK of an encryption scheme E. To authenticate a message m: • V P : Choose r R {0, 1}n and random bits 2{0, 1}* Send Y=E(PK, m°r, ) • P V : Verify that prefix of plaintext is indeed m. If yes - send r. V accepts iff the received r’=r Is it Unforgeable? Is it Deniable

Security of the scheme Unforgeability: depends on the strength of E • Sensitive to malleability: – if given E(PK, m°r, ) can generate E(PK, m’°r’, ’) where m’ is related to m and r’ is related to x then can forge. • The protocol allows a chosen ciphertext attack on E. – Even of the post-processing kind! • Can prove that any strategy for existential forgery can be translated into a CCA strategy on E • Works even against concurrent executions. We saw an encryption scheme satisfying the desired requirements Deniability: does V retain a receipt? ? – It does not retain one for an honest V – Need to prove knowledge of r

Simulator for honest receiver Choose r R {0, 1}n. Output: h. Y=E(PK, m°r, ), x, i Has exactly the same distribution as a real conversation when the verifier is following the protocol Statistical indistinguishability Verifier might cheat by checking whether certain ciphertext have as a prefix m No known concrete way of doing harm this way

Encryption as Commitment When the public key PK is fixed and known Y=E(PK, x, ) can be seen as commitment to x To open x: reveal , the random bits used to create Y Perfect binding: from unique decryption For any Y there are no two different x and x’ and ’ s. t. Y=E(PK, x, ) =E(PK, x’, ’) Secrecy: no information about x is leaked to those not knowing private key PS

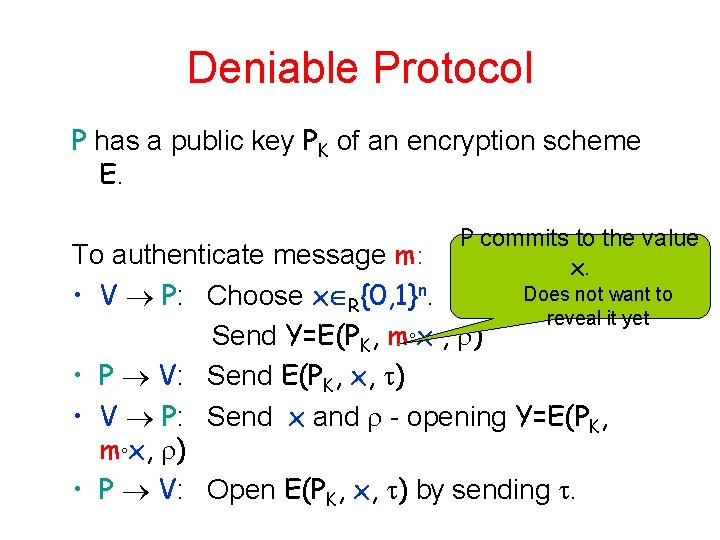
Deniable Protocol P has a public key PK of an encryption scheme E. P commits to the value x. To authenticate message m: Does not want to • V P: Choose x R{0, 1}n. reveal it yet Send Y=E(PK, m°x , ) • P V: Send E(PK, x, ) • V P: Send x and - opening Y=E(PK, m°x, ) • P V: Open E(PK, x, ) by sending .

Security of the scheme Unforgeability: as before - depends on the strength of E can simulate previous scheme (with access to D(PK , . )) Important property: E(PK, x, ) is a non-malleable commitment (wrt the encryption) to x. Deniability: can run simulator: • Extract x by running with E(PK, garbage, ) and rewinding • Expected polynomial time • Need the semantic security of E - it acts as a commitment scheme

Ring Signatures and Authentication Want to keep the sender anonymous by proving that the signer is a member of an ad hoc set – Other members do not cooperate – Use their `regular’ public-keys – Should be indistinguishable which member of the set is actually doing the authentication Bob Alice? Eve

Ring Authentication Setting • A ring is an arbitrary set of participants including the authenticator • Each member i of the ring has a public encryption key PKi – Only i knows the corresponding secret key P Si • To run a ring authentication protocol both sides need to know PK 1, PK 2, …, PKn the public keys of the ring members. . .

An almost Good Ring Authentication Protocol Ring has public keys PK 1, PK 2, …, PKn of encryption scheme E To authenticate message m with jth decryption key PSj: V P: Choose x {0, 1}n. Send E(PK 1, m°x, r 1), E(PK 2, m°x, r 2), …, E(PKn, m°x, rn) P V: Decrypt E(PKj, m°x, rj), using PSj and Send E(PK 1, x, 1), E(PK 2, x, 2), …, E(PKn, x, n) V P: open all the E(PKi, m°x, ri) by Send x and r 1, r 2 , … rn P V: Verify consistency and open all E(PKi, x, ti) by Send t 1, 2 , … n Problem: what if not all suffixes (x‘s) are equal?

The Ring Authentication Protocol Ring has public keys PK 1, PK 2, …, PKn of encryption scheme E To authenticate message m with jth decryption key PS : j V P: Choose x {0, 1}n. Send E(PK 1, m°x, r 1), E(PK 2, m°x, r 2), …, E(PK 1, m°x, rn) P V: Decrypt E(PKj, m°x, rj), using PSj and Send E(PK 1, x 1, t 1), E(PK 2, x 2, t 2), …, E(PKn, xn, tn) Where x=x 1+x 2 + xn V P: open all the E(PKi, m°x, ri) by Send x and r 1, r 2 , … rn P V: Verify consistency and open all E(PKi, x, ti) by Send t 1, t 2 , … tn and x 1, x 2 , …, x

Complexity of the scheme Sender: single decryption, n encryptions and n encryption verifications Receiver: n encryptions and n encryption verifications Communication Complexity: O(n) public-key encryptions

Security of the scheme Unforgeability: as before (assuming all keys are well chosen) since E(PK 1, x 1, t 1), E(PK 2, x 2, t 2), …, E(PK 1, xn, tn) where x=x 1+x 2 + xn is a non-malleable commitment to x Source Hiding: which key was used (among well chosen keys) is – Computationally indistinguishable during protocol – Statistically indistinguishable after protocol • If ends successfully Deniability: Can run simulator `as before’

Universal One-Way Hash functions UOWHFs • A family of functions G={g|g: {0, 1}n → {0, 1}h(n)} Such that • Easy to sample g from G and g G has succinct description • Given (n, g, x) easy to compute g(x) • h(n) < n • Hard to find target collisions: – Given (n, g, x) hard to find x’ {0, 1}n where x ≠ x’ but g(x)=g(x’) Adversary picks x before

Sources • Dolev, Dwork and Naor: Non Malleable Cryptography, Siam J. computing 2000. also Siam Review 2003 • Peikert and Waters, Lossy Trapdoor Functions and Their Applications, STOC 2008. • Rosen and Segev, Chosen Ciphertext Security via Correlated Products, TCC 2009. • Naor, Deniable Ring Authentication, Crypto 2002

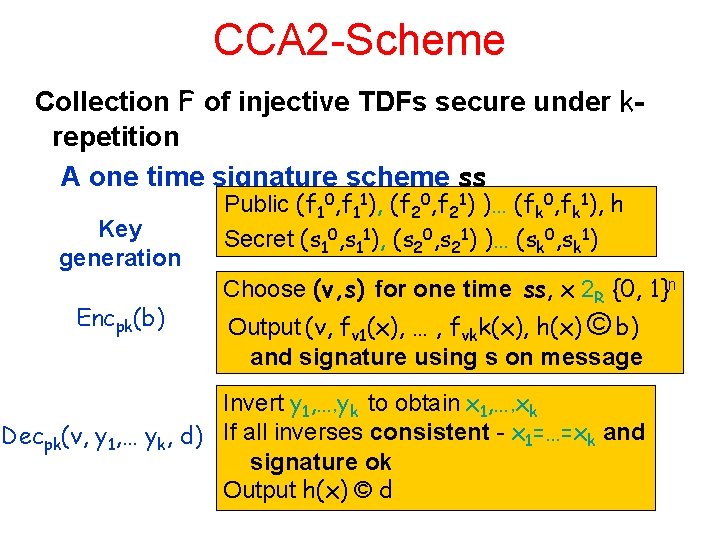
CCA 2 -Scheme Collection F of injective TDFs secure under krepetition A one time signature scheme ss Key generation Encpk(b) Public (f 10, f 11), (f 20, f 21) )… (fk 0, fk 1), h Secret (s 10, s 11), (s 20, s 21) )… (sk 0, sk 1) Choose (v, s) for one time ss, x 2 R {0, 1}n Output (v, fv 1(x), … , fvkk(x), h(x) © b) and signature using s on message Invert y 1, …, yk to obtain x 1, …, xk Decpk(v, y 1, … yk, d) If all inverses consistent - x 1=…=xk and signature ok Output h(x) © d