Topics in Cryptography Lecture 5 Topic Chosen Ciphertext

Topics in Cryptography Lecture 5 Topic: Chosen Ciphertext Security Lecturer: Moni Naor

Recap: chosen ciphertext security • Why chosen ciphertext/malleability matters • Taxonomy of Attacks and Security • Ideas for achieving CCA – Redundancy + Verification • Simple scheme achieving CCA 1 – Based on DDH

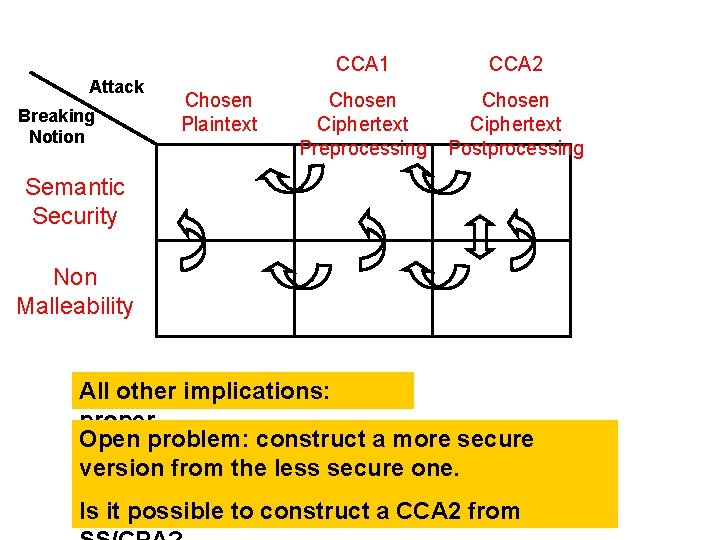
Attack Breaking Notion Chosen Plaintext CCA 1 CCA 2 Chosen Ciphertext Preprocessing Chosen Ciphertext Postprocessing Semantic Security Non Malleability All other implications: proper Open problem: construct a more secure version from the less secure one. Is it possible to construct a CCA 2 from

Ideas for achieving resistance to CCA • Add redundancy - hard to generate frivolous ciphertexts • Add methods to check consistency – This is the trickiest part: • Non interactive zero-knowledge • Specific schemes • Decrypt only if given ciphertext passes the consistency checks Important point: may decrypt with several different private keys C 1 C 2 Proof of consistency

How to prove Consistency? Zero-Knowledge proof system for language L Prover Verifier • Soundness If 2 x L Verifier rejects whp • Completeness: If x 2 L Verifier accepts • Zero Knowledge: there exists a simulator producing similar looking transcripts

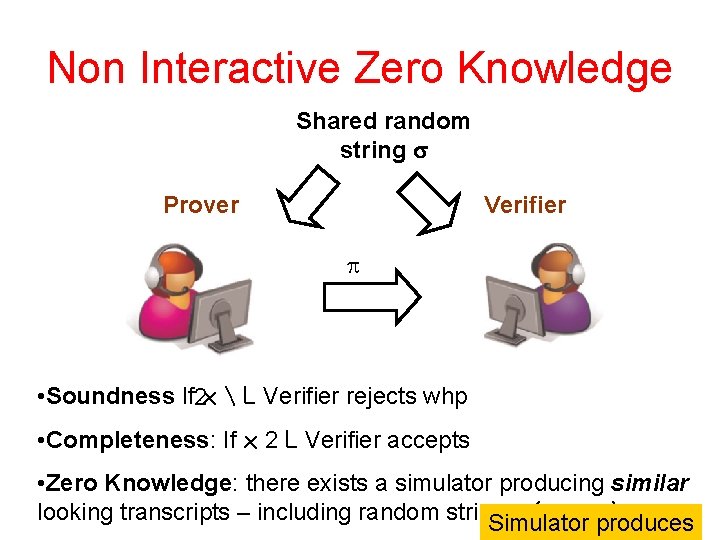
Non Interactive Zero Knowledge Shared random string Prover Verifier • Soundness If 2 x L Verifier rejects whp • Completeness: If x 2 L Verifier accepts • Zero Knowledge: there exists a simulator producing similar looking transcripts – including random string – ( , , produces x) Simulator

NIZK Relevant for soundness and zk For full specification need to clarify • When is x chosen – before or after ? – Adaptive • What does the simulator get? • Does soundness need to hold given a simulated – Cannot hold for simulated (false statement) – Simulation soundness For NP: Can be based on the existence of trapdoor permutations

• Achieving resistance to CCA with NIZK Two independent keys of some ``good” PKC KP 1 and K P 2 • A public random string for NIZK of the language {(KP 1, KP 2, C 1, C 2)| C 1 and C 2 encrypt the same message} Important point: • To encrypt message m generate ciphertexts C 1 and C 2 may decrypt with two and add a proof of consistency different private keys – Ciphertext: C 1, C 2, • To decrypt – Verify proof and then – Decrypt only if ciphertexts passed the consistency checks C 1 C 2 Proof of consistency

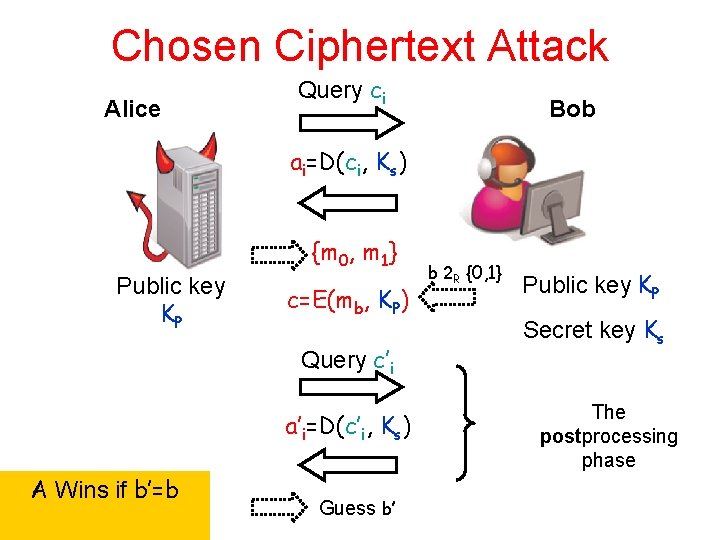
Chosen Ciphertext Attack Alice Query ci Bob ai=D(ci, Ks) {m 0, m 1} Public key KP c=E(mb, KP) Query c’i a’i=D(c’i, Ks) A Wins if b’=b Guess b’ b 2 R {0, 1} Public key KP Secret key Ks The postprocessing phase

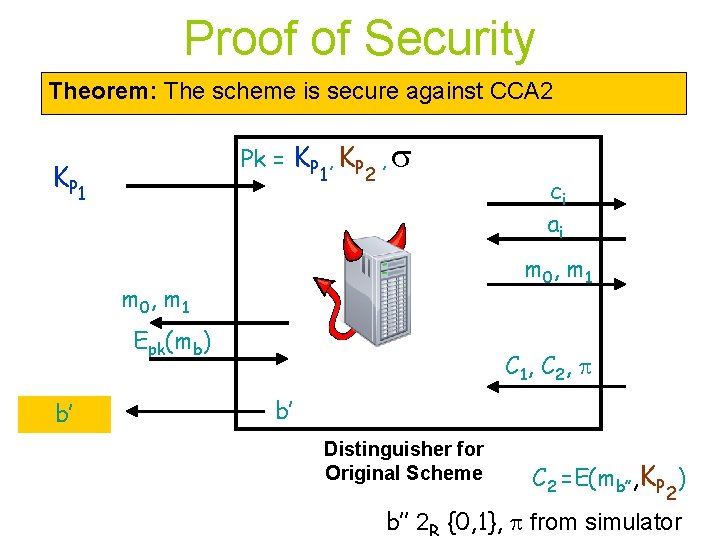
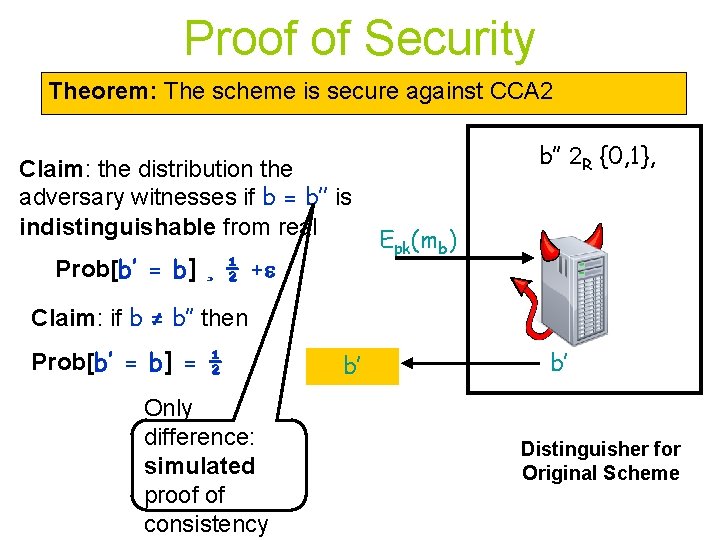
Proof of Security Theorem: The scheme is secure against CCA 2 Pk = KP , KP K P 1 1 2 , m 0, m 1 Epk(mb) b’ ci ai C 1, C 2 , b’ Distinguisher for Original Scheme C 2 =E(mb’’, KP ) 2 b’’ 2 R {0, 1}, from simulator

Proof of Security Theorem: The scheme is secure against CCA 2 Claim: the distribution the adversary witnesses if b = b’’ is indistinguishable from real Prob[b’ = b] ¸ ½ + b’’ 2 R {0, 1}, Epk(mb) Claim: if b ≠ b’’ then Prob[b’ = b] = ½ Only difference: simulated proof of consistency b’ b’ Distinguisher for Original Scheme

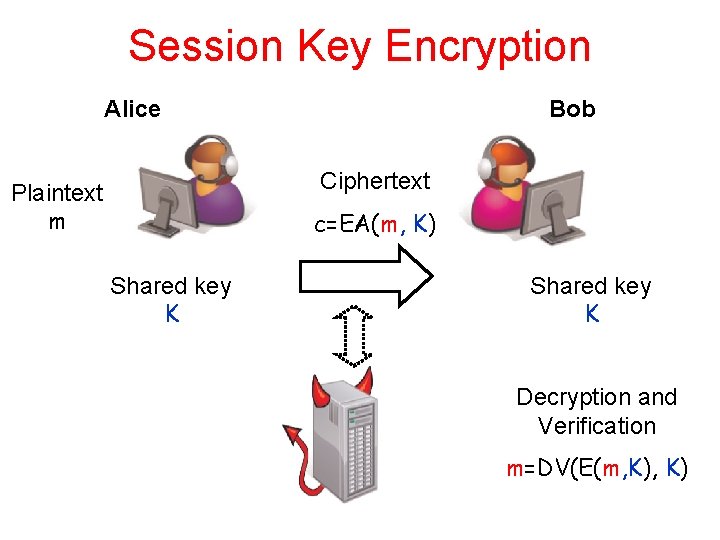
Session Key Encryption Alice Bob Ciphertext Plaintext m c=EA(m, K) Shared key K Decryption and Verification m=DV(E(m, K)

Structure of Construction: “Hybrid” Encryption: • Use public key to generate shared session key • Use shared key to encrypt + authenticate with one time scheme Decryption: • Use secret key to obtain session key • Use session decryption. Check authentication. • If fails reject. Ow output message.

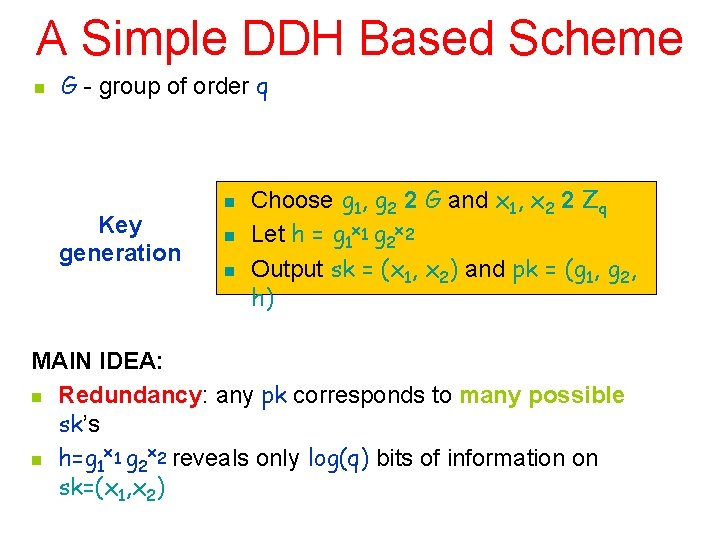
A Simple DDH Based Scheme n G - group of order q Key generation n Choose g 1, g 2 2 G and x 1, x 2 2 Zq Let h = g 1 x 1 g 2 x 2 Output sk = (x 1, x 2) and pk = (g 1, g 2, h) MAIN IDEA: n Redundancy: any pk corresponds to many possible sk’s x x n h=g 1 1 g 2 2 reveals only log(q) bits of information on sk=(x 1, x 2)

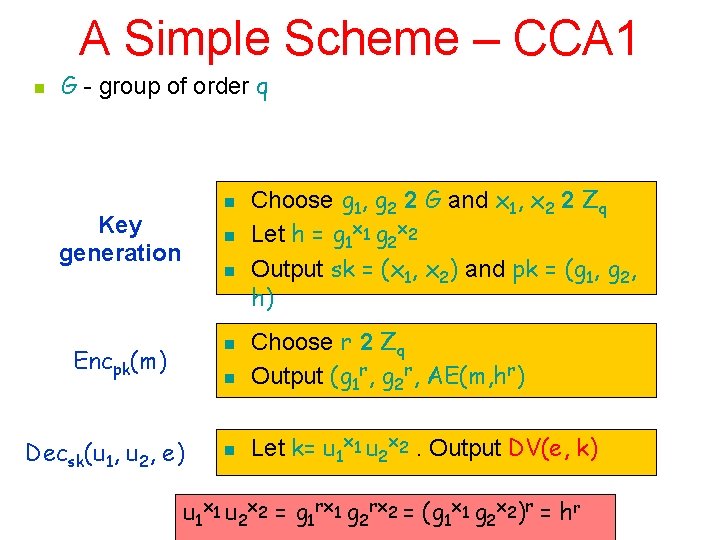
A Simple Scheme – CCA 1 n G - group of order q n Key generation n Encpk(m) n Decsk(u 1, u 2, e) n Choose g 1, g 2 2 G and x 1, x 2 2 Zq Let h = g 1 x 1 g 2 x 2 Output sk = (x 1, x 2) and pk = (g 1, g 2, h) Choose r 2 Zq Output (g 1 r, g 2 r, AE(m, hr) Let k= u 1 x 1 u 2 x 2. Output DV(e, k) u 1 x 1 u 2 x 2 = g 1 rx 1 g 2 rx 2 = (g 1 x 1 g 2 x 2)r = hr

Key property for security: no invalid ciphertexts accepted n Given the public key pk = (g 1, g 2, h) one linear equation is known on x 1, x 2 n n Given h = g 1 x 1 g 2 x 2. Still log q entropy Claim: this entropy is kept during the query-attack phase n In legitimate query ciphertexts: (v 1=g 1 r, v 2=g 2 r) and AE(m, k)) and the decryption is independent of x 1, n x 2 In invalid query ciphertexts: (v 1=g 1 r, v 2=g 2 r’) and AE(m, k)) is rejected whp challenge ciphertext is known Not clear what happens when during the attack

Generalizing leftover hash lemma To assure independence make sure that AE(m, hr) does not leak information about hr • Have a family of four-wise independent functions – For each 2 : G {0, 1}ℓ

The Modified Scheme n n G - group of order q a family of four-wise independent functions n Choose g 1, g 2 2 G, x 1, x 2 2 Zq and 2 R Let h = g 1 x 1 g 2 x 2 Key generation n n Output sk = (x 1, x 2) and pk = (g 1, g 2, h, ) Encpk(m) n Choose r 2 Zq n Output (g 1 r, g 2 r, AE(m, (hr)) n Let k= (u 1 x 1 u 2 x 2). Output DV(e, k) Decsk(u 1, u 2, e) u 1 x 1 u 2 x 2 = g 1 rx 1 g 2 rx 2 = (g 1 x 1 g 2 x 2)r = hr

Generating the Challenge Theorem: The scheme is secure against CCA 1 (g 1, g 2, g 1 r 1, g 2 r 2 , ) pk ci Generating pk given (g 1, g 2, g 1 r 1, g 2 r 2) n. Choose x 1, x 2 2 Zq x x n. Let h = g 1 1 g 2 2 n. Output pk = (g 1, g 2, h) and remember sk = (x 1, x 2) Let k= g 1 r 1 x 1 g 2 r 2 x 2 Output (g 1 r 1, g 2 r 2, AE(mb, (k))) ai m 0, m 1 Epk(mb) Distinguisher for DDH

Min-Entropy For a probability distribution X over {0, 1}n H 1(X) = - log maxx Pr[X = x] Represents the probability of the most likely value of X X is a k-source if H 1(X) ¸ k (i. e. , Pr[X = x] · 2 -k for all x) Statistical distance: ¢(X, Y) = a |Pr[X=a] – Pr[Y=a]|

Extractors Universal procedure for “purifying” an imperfect source Definition: Ext: {0, 1}n £ {0, 1}d ! {0, 1}ℓ is a (k, )-extractor if: for any k-source X ¢(Ext(X, Ud), Uℓ) · k-source of length n x “seed” d random bits s EXT ℓ almost-uniform bits

Strong Extractors Output looks random even after seeing the seed Definition: Ext: {0, 1}n £ {0, 1}d ! {0, 1}ℓ is a (k, )-strong extractor if Ext’(x, s) = s ◦ Ext(x, s) is a (k, )-extractor Leftover hash lemma [ILL 89]: Pairwise independent hash functions are strong extractors Example: Ext(x, (a, b)) = first ℓ bits of ax+b over GF[2 n] n n Output length ℓ = k – 2 log(1/ ) Seed length d = 2 n, almost pairwise independence d = O(log n +

Generalizing leftover hash lemma 2(ℓ- )/2 Leftover hash lemma [ILL 89]: Pairwise independent hash functions are strong extractors ( , (X)) is close to uniform provided X has sufficient min entropy New lemma [KPSY 09]: If (X, X’) are random variables such that • H 1(X), H 1(X’) ¸ • Prob[X=X’] = 0 • 2 R where is four-wise independent and (X) 2 {0, 1}ℓ Then ( , (X), (X’)) is 2ℓ- /2 close to uniform

The Modified Scheme n n G - group of order q a family of four-wise independent function Encpk(m) Decsk(u 1, u 2, e) (u 1, u 2) form challenge n Choose r 2 Zq n Output (g 1 r, g 2 r, AE(m, (hr)) n Let k = (u 1 x 1 u 2 x 2). Output DV(e, k) (u’ 1, u’ 2) from adversary generated query (x 1, x 2) have log q bits of entropy For (u 1, u 2 ) and (u’ 1, u’ 2) Let X = u 1 x 1 u 2 x 2 and X’= u’ 1 x 1 u’ 2 x 2 Provided ( u 1 , u 2 ) Given (X) no information is leaked about (X’) (u’ , u’ ) 1 2

Proof: summing up During the attack: • Chance for invalid ciphertext not labeled as such: Number of ciphertexts queried t ¢ Pr[forgery in AE] • Entropy of (x 1, x 2) decreased by this amount Challenge ciphertext valid or not depending on whether the input is in DDH or not. • If original adversary wins the game with probability ½+ • Advantage in distinguishing DDH from non-DDH is

Correlated Products of trapdoors One-Way Functions • Easy to evaluate: x 7→ f(x) • Hard to invert: For any efficient algorithm A Prob[A(f(x)) ∈ f− 1(f(x))] is negligible • Injective trapdoor functions (f, f− 1) ← F

Correlated Products One-Way Functions • Easy to evaluate: x 7→ f(x) • Hard to invert: For any efficient algorithm A Pr A(f(x)) ∈ f− 1(f(x)) is negligible • Injective trapdoor functions (f, f− 1) ← F TDF

Correlated Products • For a collection F of one-way functions consider (f 1(x 1), . . . , fk(xk)) for every f 1, . . . , fk ∈F. • f 1, . . . , fk is hard to invert for random (x 1, … , x k) • But what happens when x 1, … , xk are correlated?

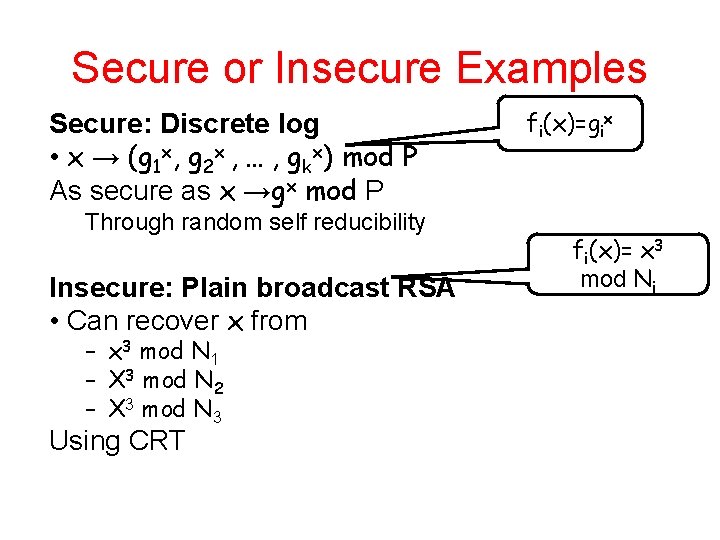
Secure or Insecure Examples Secure: Discrete log • x → (g 1 x, g 2 x , … , gkx) mod P As secure as x →gx mod P Through random self reducibility Insecure: Plain broadcast RSA • Can recover x from – x 3 mod N 1 – X 3 mod N 2 – X 3 mod N 3 Using CRT fi(x)=gix fi(x)= x 3 mod Ni

Security Under Correlated Products Definition: • F is secure under a C-correlated product if for any efficient A Pr[A(f 1, …, fk, f 1(x 1), …, fk(xk)) = (x 1, …, xk)] is negligible, where f 1, … , fk ← F and (x 1, . . . , xk) ← C. Natural correlations • x 1 = x 2 … = xk k-repetition • (x 1, … , xk) are ℓ-wise independent for ℓ < k

Reminder: CPA-Security from TDFs Collection F of injective • Hard-core bit h for F – Given f(x) infeasible to guess h(x) with a noticeable advantage The scheme: • Key generation: (pk, sk) = (f, f− 1) • Encryption: Enc(pk, b) = (f(x), h(x)©b) for x 2 R {0, 1}n • Decryption: Dec(sk, (c, d)) = h(f− 1(c)) © d

CCA-Security from Repetition Collection F of injective TDFs secure under k-repetition product • Hard-core bit h for F – Given f(x) infeasible to guess h(x) with a noticeable advantage Goldreich-Levin (inner product) is still hard core

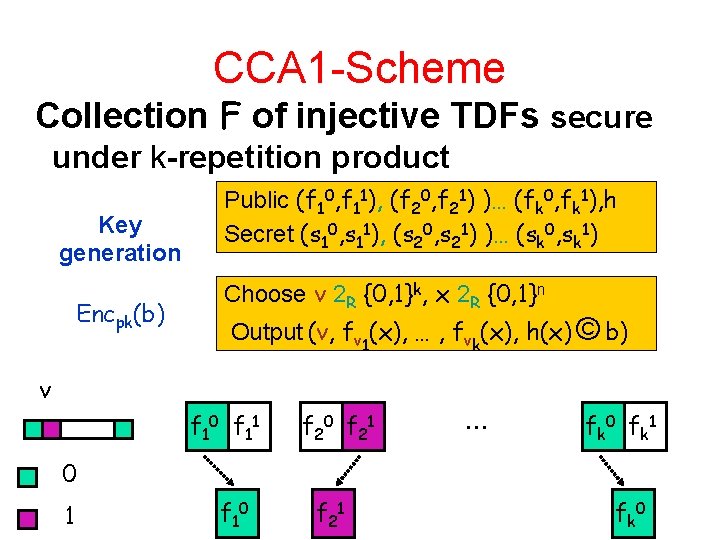
CCA 1 -Scheme Collection F of injective TDFs secure under k-repetition product Key generation Encpk(b) Public (f 10, f 11), (f 20, f 21) )… (fk 0, fk 1), h Secret (s 10, s 11), (s 20, s 21) )… (sk 0, sk 1) Choose v 2 R {0, 1}k, x 2 R {0, 1}n Output (v, fv 1(x), … , fvk(x), h(x) © b) v f 10 f 11 f 20 f 21 … f k 0 f k 1 0 1 f 10 f 21 f k 0

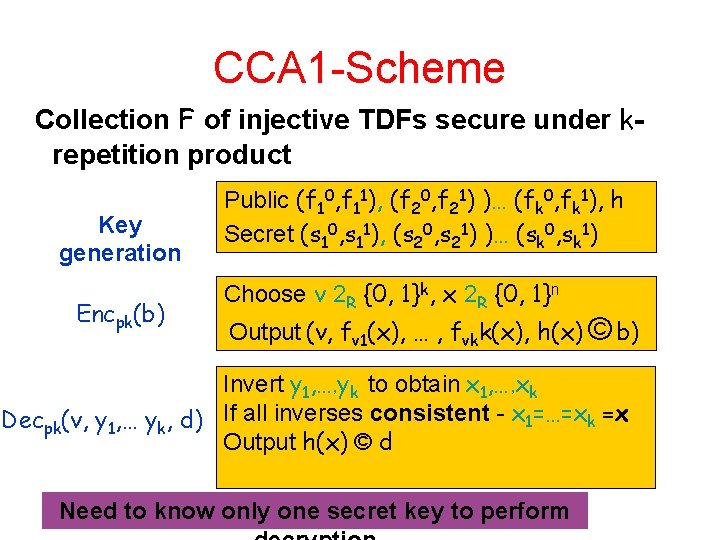
CCA 1 -Scheme Collection F of injective TDFs secure under krepetition product Key generation Encpk(b) Public (f 10, f 11), (f 20, f 21) )… (fk 0, fk 1), h Secret (s 10, s 11), (s 20, s 21) )… (sk 0, sk 1) Choose v 2 R {0, 1}k, x 2 R {0, 1}n Output (v, fv 1(x), … , fvkk(x), h(x) © b) Invert y 1, …, yk to obtain x 1, …, xk Decpk(v, y 1, … yk, d) If all inverses consistent - x 1=…=xk =x Output h(x) © d Need to know only one secret key to perform

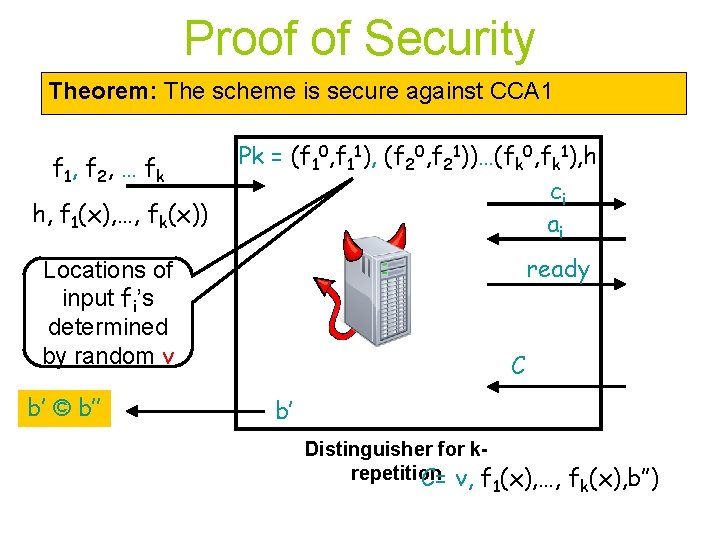
Proof of Security Theorem: The scheme is secure against CCA 1 f 1, f 2 , … f k h, f 1(x), …, fk(x)) Pk = (f 10, f 11), (f 20, f 21))…(fk 0, fk 1), h ci ai ready Locations of input fi’s determined by random v b’ © b’’ C b’ Distinguisher for krepetition C= v, f 1(x), …, fk(x), b’’)

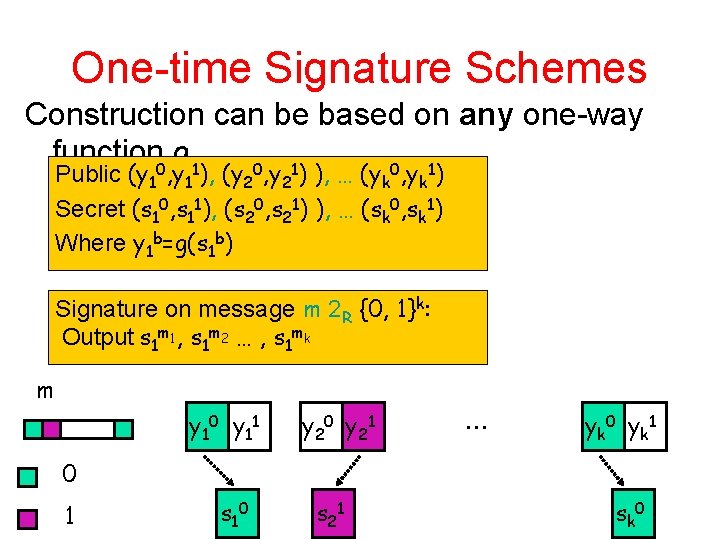
One-time Signature Schemes A signature scheme that is • Existentially unforgeable • Adversary A gets to pick and see signature on one message A Wins if he can find any other (message, signature) that is accepted by signature verification algorithm – Message should be different – Strongly unforgeable: also cannot find another signature to a message that has been signed

One-time Signature Schemes Construction can be based on any one-way function 0 g 1 0 1 Public (y 1 , y 1 ), (y 2 , y 2 ) ), … (yk , yk ) Secret (s 10, s 11), (s 20, s 21) ), … (sk 0, sk 1) Where y 1 b=g(s 1 b) Signature on message m 2 R {0, 1}k: Output s 1 m 1, s 1 m 2 … , s 1 mk m y 10 y 11 y 20 y 21 … y k 0 y k 1 0 1 s 10 s 21 s k 0

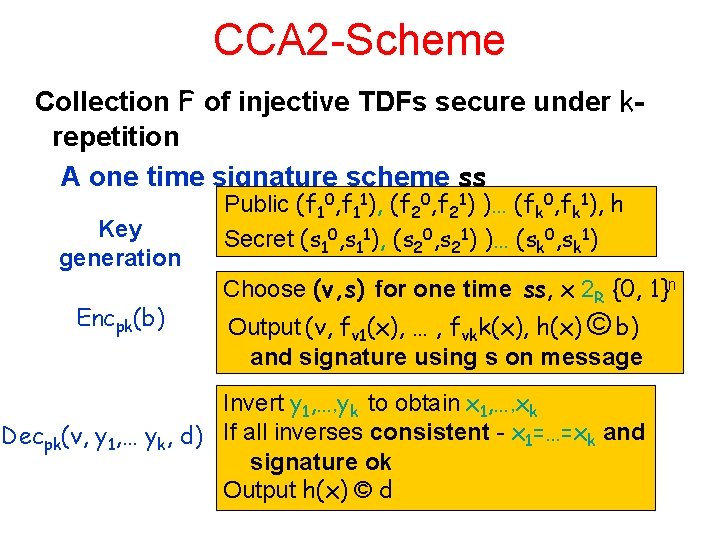
CCA 2 -Scheme Collection F of injective TDFs secure under krepetition A one time signature scheme ss Key generation Encpk(b) Public (f 10, f 11), (f 20, f 21) )… (fk 0, fk 1), h Secret (s 10, s 11), (s 20, s 21) )… (sk 0, sk 1) Choose (v, s) for one time ss, x 2 R {0, 1}n Output (v, fv 1(x), … , fvkk(x), h(x) © b) and signature using s on message Invert y 1, …, yk to obtain x 1, …, xk Decpk(v, y 1, … yk, d) If all inverses consistent - x 1=…=xk and signature ok Output h(x) © d

Homework: One time Signature Schemes • Show that if g is a one-way function the scheme is indeed a one-time signature scheme. • Show to obtain a strongly unforgeable signature scheme – You may use the existence of Universal One-way Hash Functions • Why do we need strongly unforgeable signature schemes in the CCA 2 scheme?

Universal One-Way Hash functions UOWHFs • A family of functions G={g|g: {0, 1}n → {0, 1}h(n)} Such that • Easy to sample g from G and g G has succinct description • Given (n, g, x) easy to compute g(x) • h(n) < n • Hard to find target collisions: – Given (n, g, x) hard to find x’ {0, 1}n where x ≠ x’ but g(x)=g(x’) Adversary picks x before

Interactive Authentication P wants to convince V that he is approving message m P has a public key KP of an encryption scheme E. To authenticate a message m: • V P: Choose r 2 R {0, 1}n. Send c=E(m ° r, KP) • P V : Receiving c Decrypt c using KS Verify that prefix of plaintext is m. If yes - send r. V is satisfied if he receives the same r he chose Claim: if E is CCA 2 secure, then scheme is existentially unforgeable against active adversary

Sources • Dolev, Dwork and Naor: Non Malleable Cryptography, Siam J. computing 2000. also Siam Review 2003 • Cramer and Shoup: Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack (see www. shoup. net) • Lindell: A Simpler Construction of CCA 2 -Secure Public. Key Encryption Under General Assumptions. In Eurocrypt 2003 • Kiltz, Pietrzak, Stam and Yung, A New Randomness Extraction Paradigm for Hybrid Encryption. Eurocrypt 2009. • Peikert and Waters, Lossy Trapdoor Functions and Their Applications, STOC 2008. • Rosen and Segev, Chosen Ciphertext Security via Correlated Products, TCC 2009.