Topics Descriptive Statistics A road map Examining data

Topics: Descriptive Statistics • A road map • Examining data through frequency distributions • Measures of central tendency • Measures of variability • The normal curve • Standard scores and the standard normal distribution

The Role of Description • Description as a purpose of research • Choosing the right statistical procedures

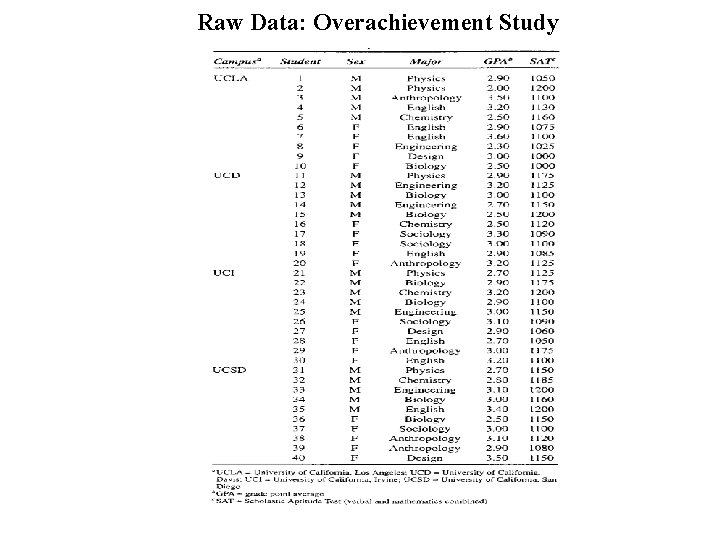
Raw Data: Overachievement Study

Frequency Distributions • A method of summarizing and highlighting aspects of the data in a data matrix, showing the frequency with which each value occurs. • Numerical Representations: a tabular arrangement of scores • Graphical Representations: a pictorial arrangement of scores

Numerical Frequency Distributions • • Ungrouped Frequency Distributions Grouped Frequency Distributions Relative Frequency Distributions Cumulative Frequency Distributions

Tabular Frequency Distributions Single-Variable (“Univariate”)

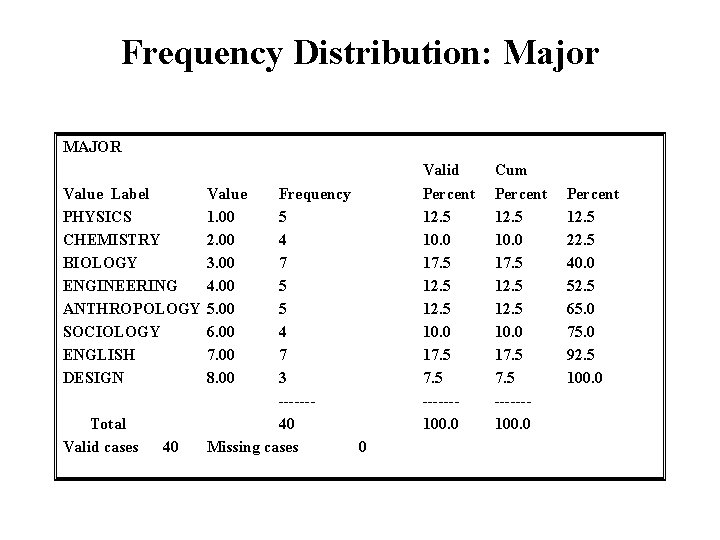
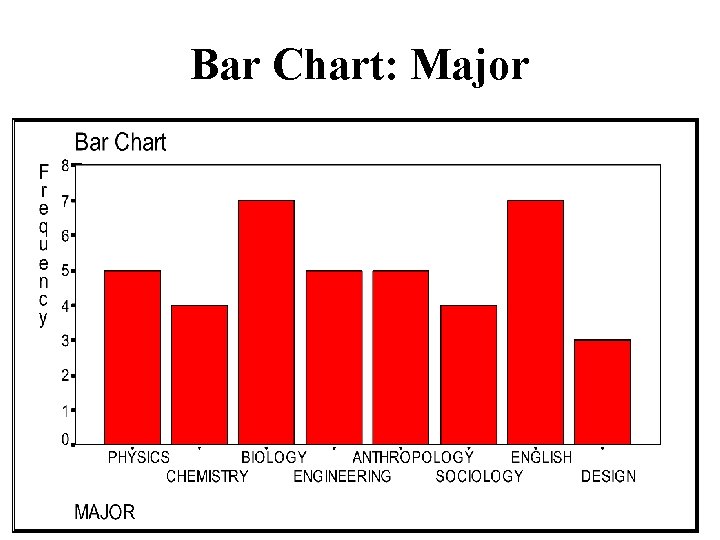
Frequency Distribution: Major MAJOR Value Label Value PHYSICS 1. 00 CHEMISTRY 2. 00 BIOLOGY 3. 00 ENGINEERING 4. 00 ANTHROPOLOGY 5. 00 SOCIOLOGY 6. 00 ENGLISH 7. 00 DESIGN 8. 00 Total Valid cases 40 Frequency 5 4 7 5 5 4 7 3 ------40 Missing cases 0 Valid Percent 12. 5 10. 0 17. 5 ------100. 0 Cum Percent 12. 5 10. 0 17. 5 ------100. 0 Percent 12. 5 22. 5 40. 0 52. 5 65. 0 75. 0 92. 5 100. 0

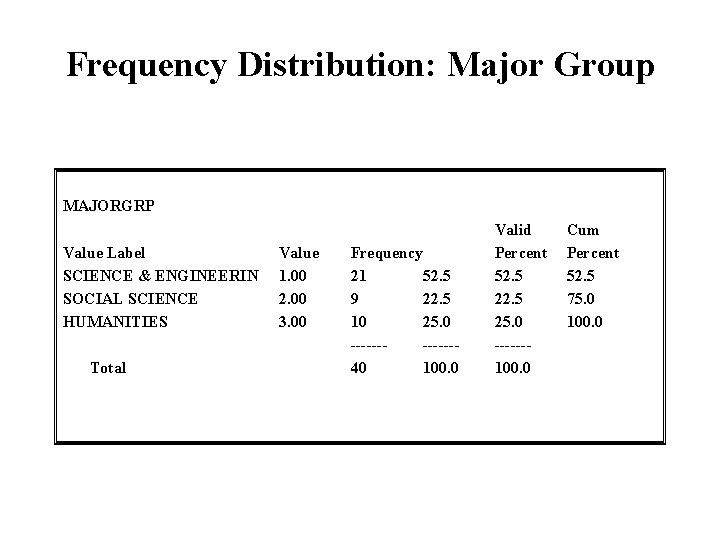
Frequency Distribution: Major Group MAJORGRP Value Label SCIENCE & ENGINEERIN SOCIAL SCIENCE HUMANITIES Total Value 1. 00 2. 00 3. 00 Frequency 21 52. 5 9 22. 5 10 25. 0 ------40 100. 0 Valid Percent 52. 5 25. 0 ------100. 0 Cum Percent 52. 5 75. 0 100. 0

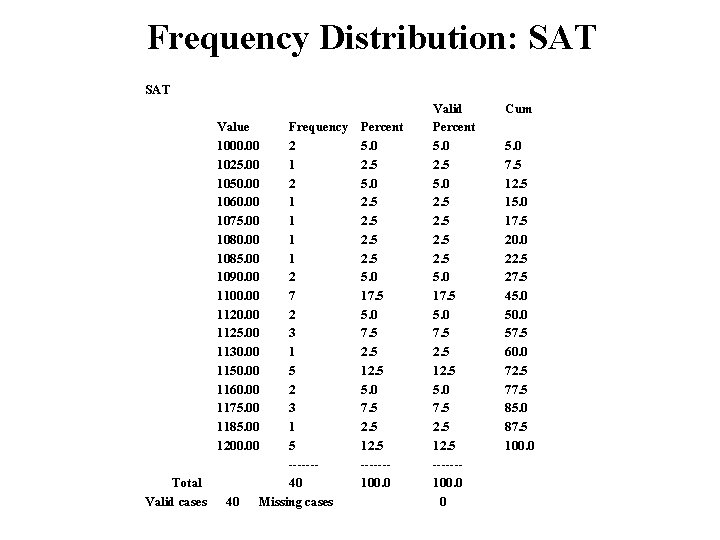
Frequency Distribution: SAT Value 1000. 00 1025. 00 1050. 00 1060. 00 1075. 00 1080. 00 1085. 00 1090. 00 1100. 00 1125. 00 1130. 00 1150. 00 1160. 00 1175. 00 1185. 00 1200. 00 Total Valid cases 40 Frequency 2 1 1 1 1 2 7 2 3 1 5 ------40 Missing cases Percent 5. 0 2. 5 2. 5 5. 0 17. 5 5. 0 7. 5 2. 5 12. 5 ------100. 0 Valid Percent 5. 0 2. 5 2. 5 5. 0 17. 5 5. 0 7. 5 2. 5 12. 5 ------100. 0 0 Cum 5. 0 7. 5 12. 5 15. 0 17. 5 20. 0 22. 5 27. 5 45. 0 50. 0 57. 5 60. 0 72. 5 77. 5 85. 0 87. 5 100. 0

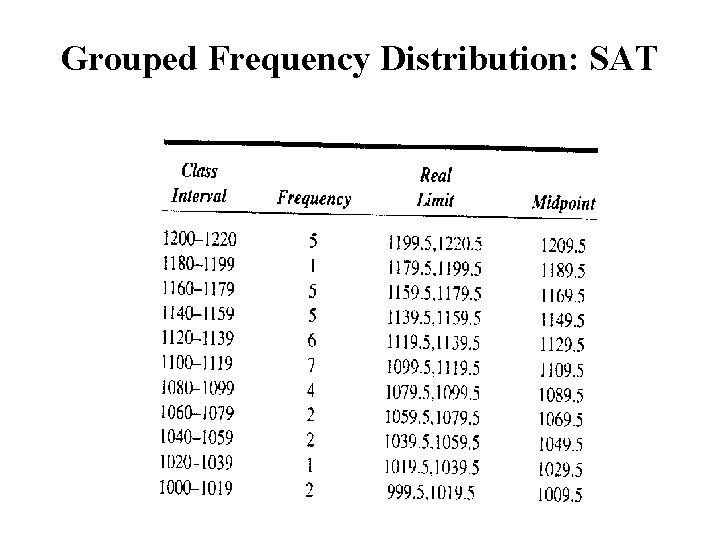
Grouped Frequency Distribution: SAT

Graphical Frequency Distributions • • • Bar Graphs Histograms Stem and Leaf Frequency Polygons Pie Chart

Graphical Frequency Distributions: Single-Variable (“Univariate”)

Bar Chart: Major

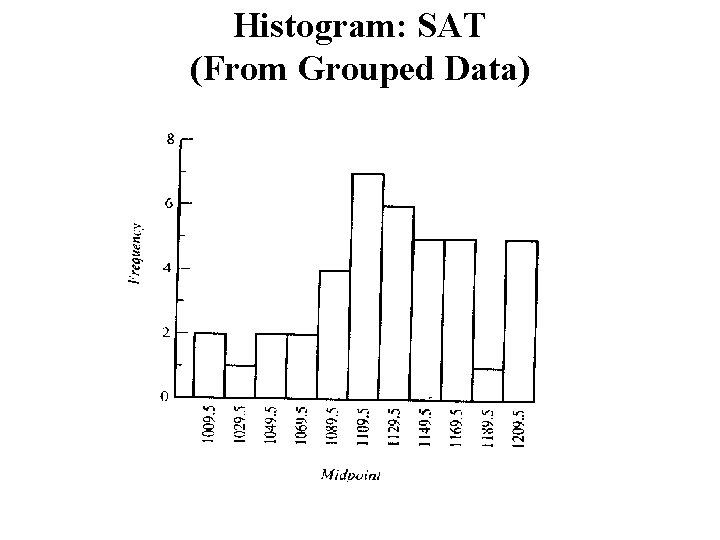
Histogram: SAT (From Grouped Data)

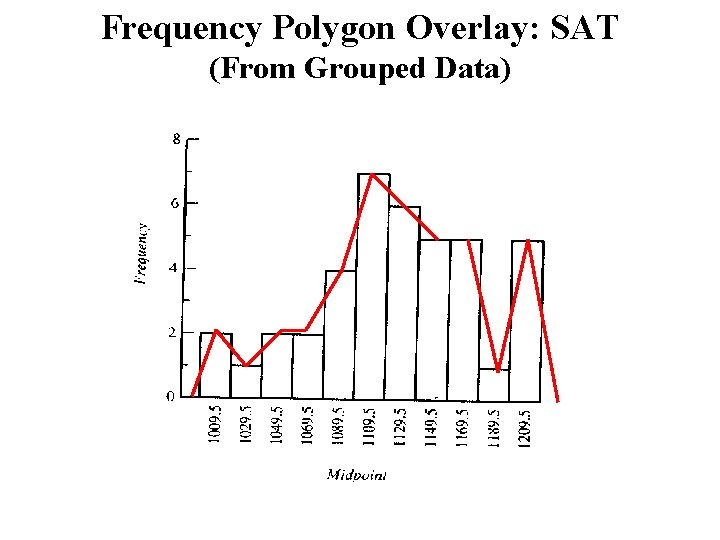
Frequency Polygon Overlay: SAT (From Grouped Data)

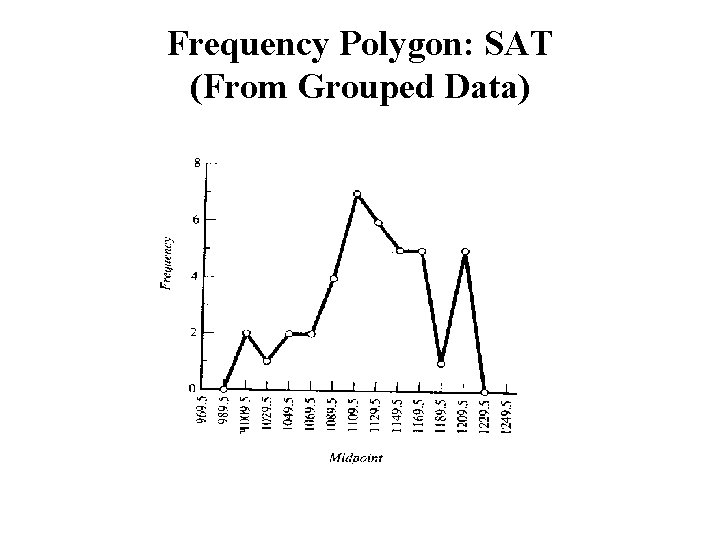
Frequency Polygon: SAT (From Grouped Data)

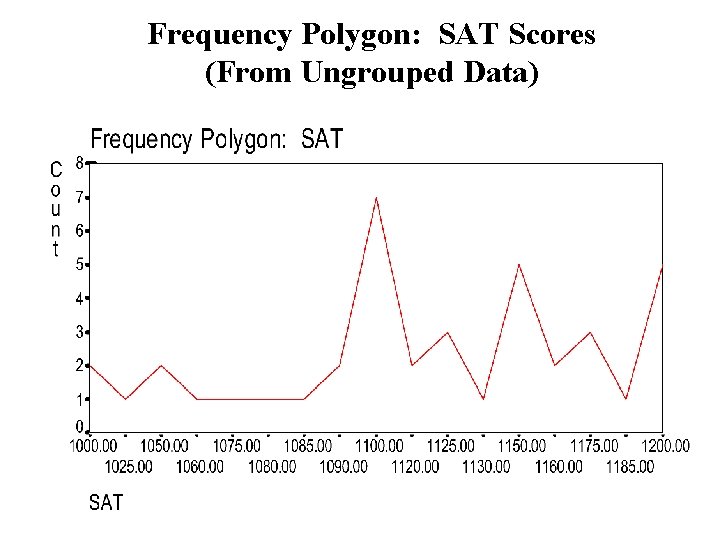
Frequency Polygon: SAT Scores (From Ungrouped Data)

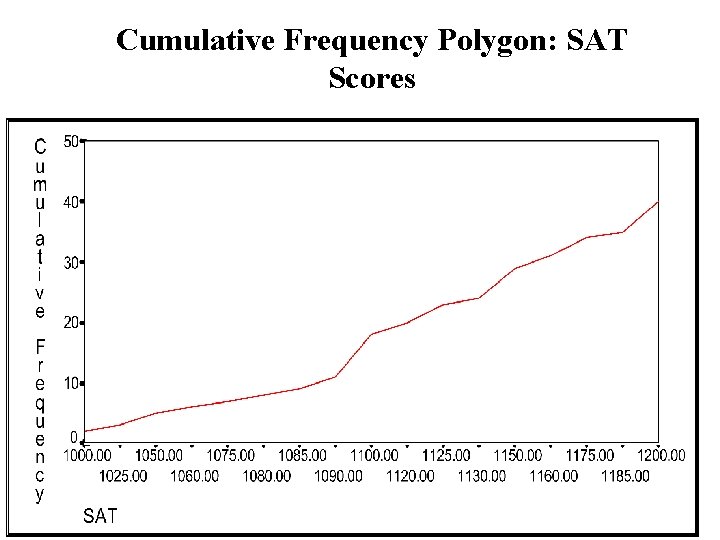
Cumulative Frequency Polygon: SAT Scores

Stem and Leaf: SAT

Stem and Leaf: SAT Stem-and-Leaf Plot Frequency 3. 00 8. 00 13. 00 11. 00 5. 00 Stem width: Each leaf: Stem & 10 10 11 11 12 . . . Leaf 002 55678899 0000000222223 55555667778 00000 100. 00 1 case(s)

Graphical Frequency Distributions Two-Variable (“Joint” or “Bivariate”)

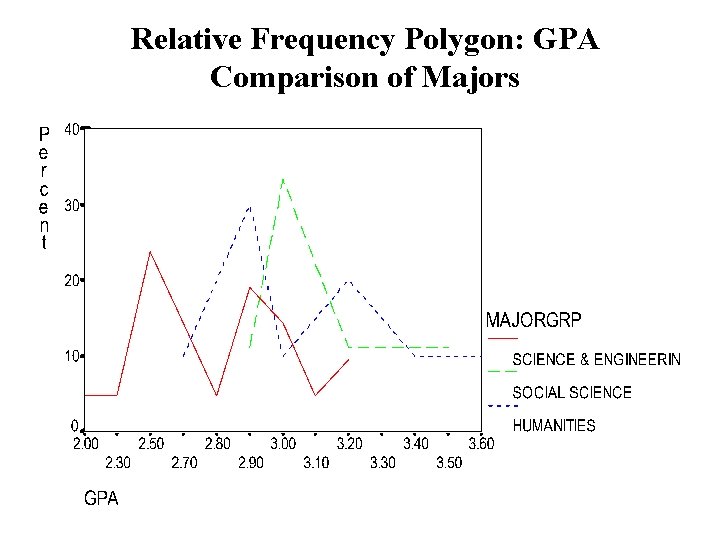
Relative Frequency Polygon: GPA Comparison of Majors

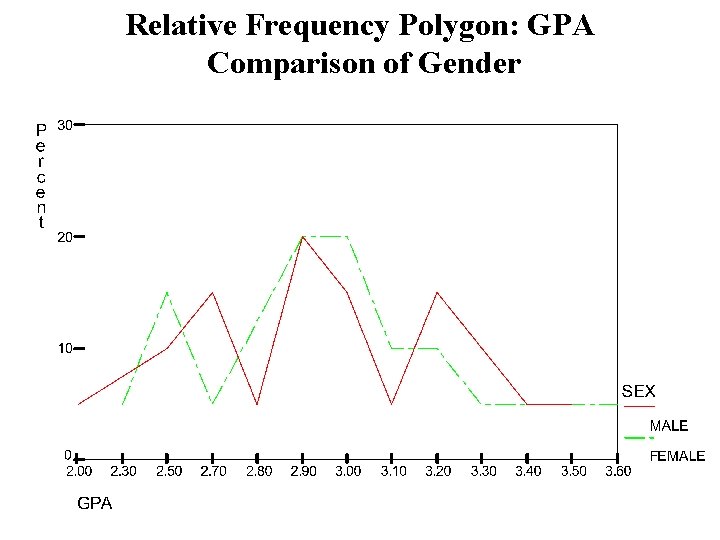
Relative Frequency Polygon: GPA Comparison of Gender

What Can Be Seen in Frequency Distributions • Shape • Central Tendency • Variability

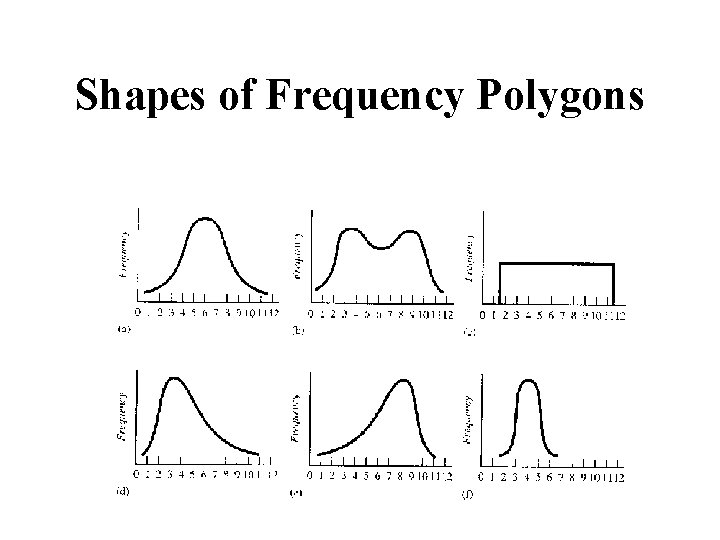
Shapes of Frequency Polygons

Shapes of Distributions

Descriptive Statistics • Central Tendency – Mode – Median – Mean • Variability – Range – Standard Deviation – Variance

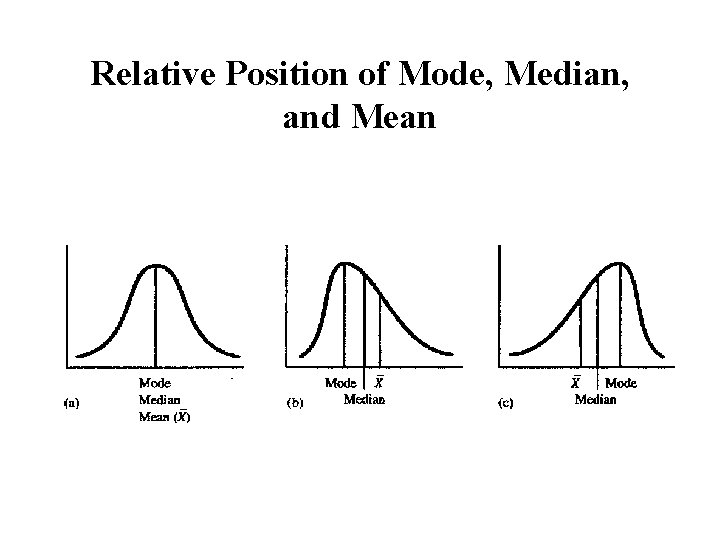
Definitions: Measures of Central Tendency • Mean: – “Arithmetic mean” – “Center of gravity” such that the “weight” of the scores above the mean exactly balances the “weight” of the scores below the mean • Median: – The number that lies at the midpoint of the distribution of scores; divides the distribution into two equal halves • Mode: – Most frequently occurring score

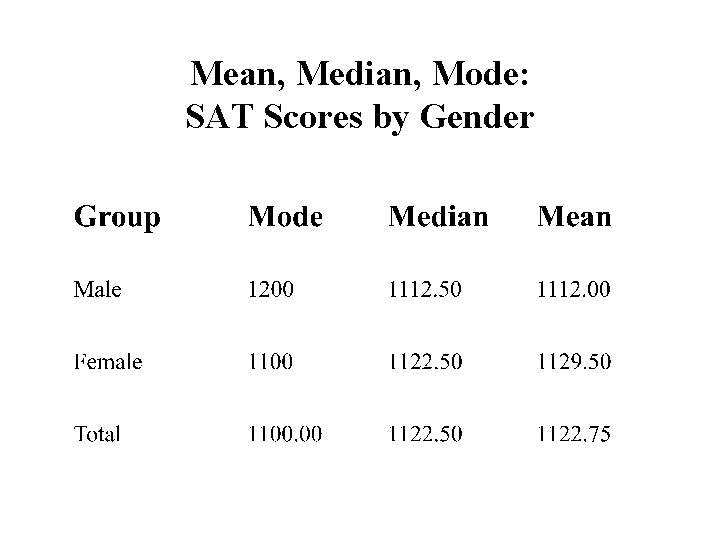
Mean, Median, Mode: SAT Scores by Gender

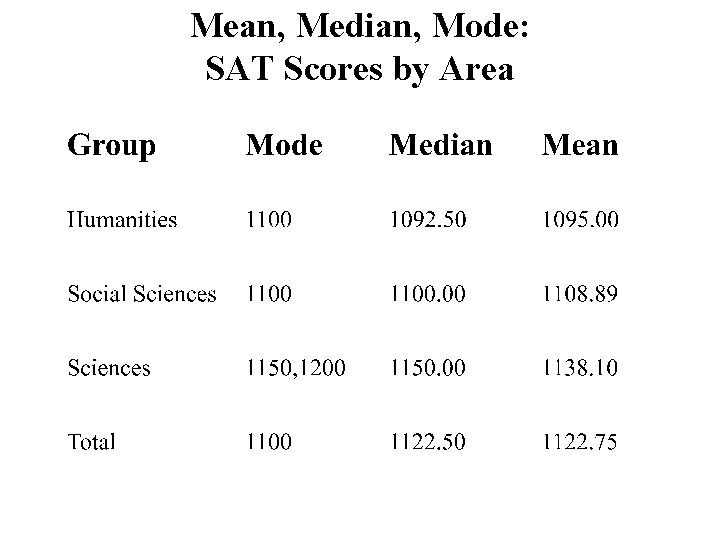
Mean, Median, Mode: SAT Scores by Area

Relative Position of Mode, Median, and Mean

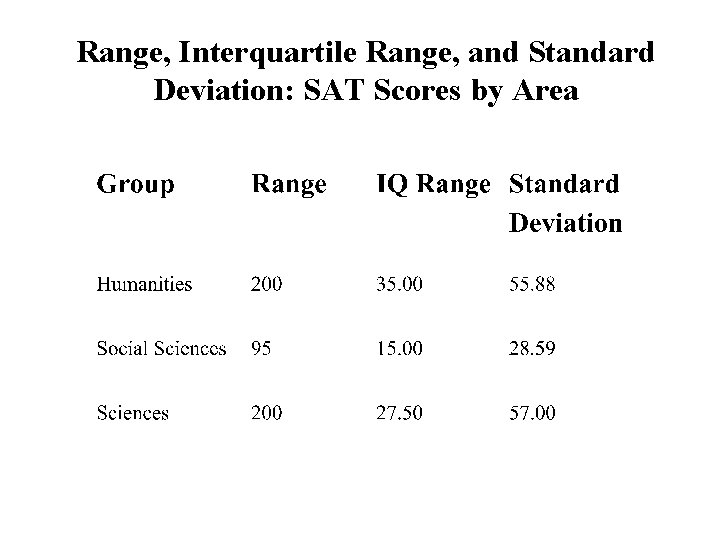
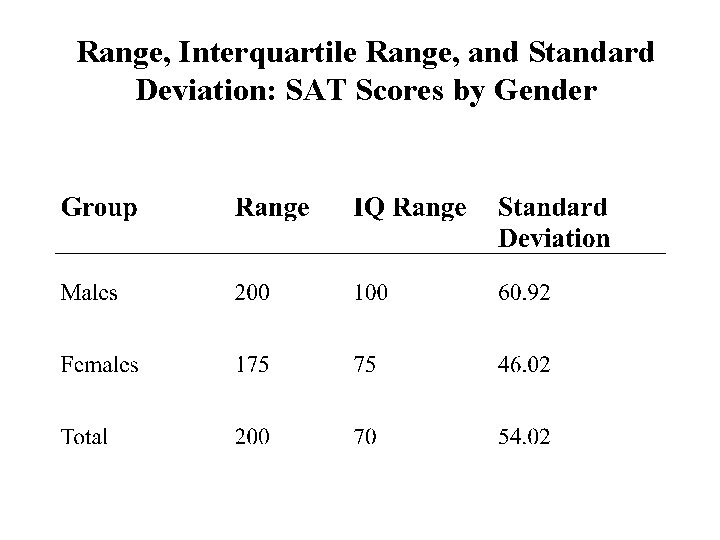
Definitions: Measures of Variability • Range: – Difference between highest and lowest score • Inter-quartile Range: – The spread of the middle 50% of the scores – The difference between the top 25% (Upper Quartile-Q 3) and the lower 25% (Lower Quartile-Q 1) • Standard Deviation: – The average dispersion or deviation of scores around the mean (measured in original score units) • Variance: – The average variability of scores (measured in squared units of the original scores (square of the standard deviation)

Range, Interquartile Range, and Standard Deviation: SAT Scores by Area

Range, Interquartile Range, and Standard Deviation: SAT Scores by Gender

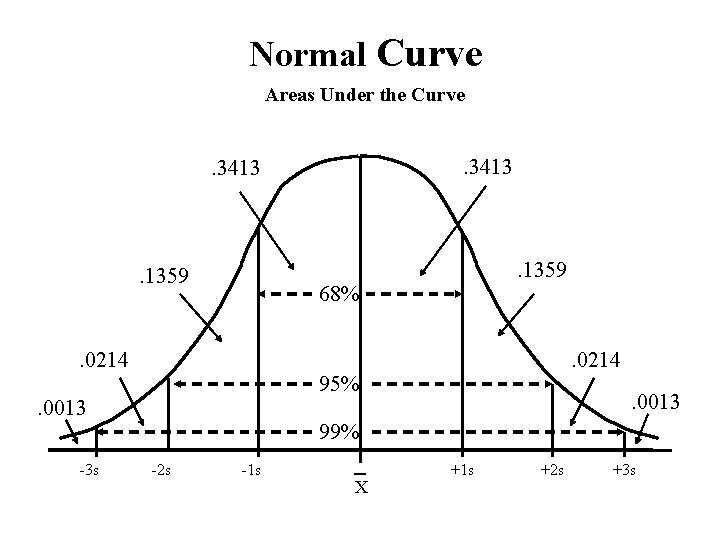
Properties of Normal Distribution • Bell-shaped (unimodal) • Symmetric about the mean • Mode, median, and mean are equal (though rarely occurs) • Asymptotic (curve never touches the abscissa)

Normal Curve Areas Under the Curve . 3413 . 1359 68% . 0214 95% . 0013 -3 s . 1359 . 0013 99% -2 s -1 s X +1 s +2 s +3 s

Definitions: Standard Scores • Standard Scores: scores expressed as SD away from the mean (z-scores) • Obtained by finding how far a score is above or below the mean and dividing that difference by the SD • Changes mean to 0 and SD to 1, but does not change the shape (called Standard Normal Distribution)

Uses of Standard Normal Distribution • What proportion of scores falls between the mean and a given raw score • What proportion of scores falls above or below a given raw score • What proportion of scores falls between two raw scores • What raw score fall above (or below) a certain percentage of scores