Topics Basic Definitions Sequential circuits State variables state

Topics • Basic Definitions – Sequential circuits – State variables, state tables, state diagrams • Latches • Metastability Lect #10 Rissacher EE 365

Sequential Circuits • Output depends on current input and past history of inputs. • “State” embodies all the information about the past needed to predict current output based on current input. – State variables, one or more bits of information which define the state of the system. Lect #10 Rissacher EE 365

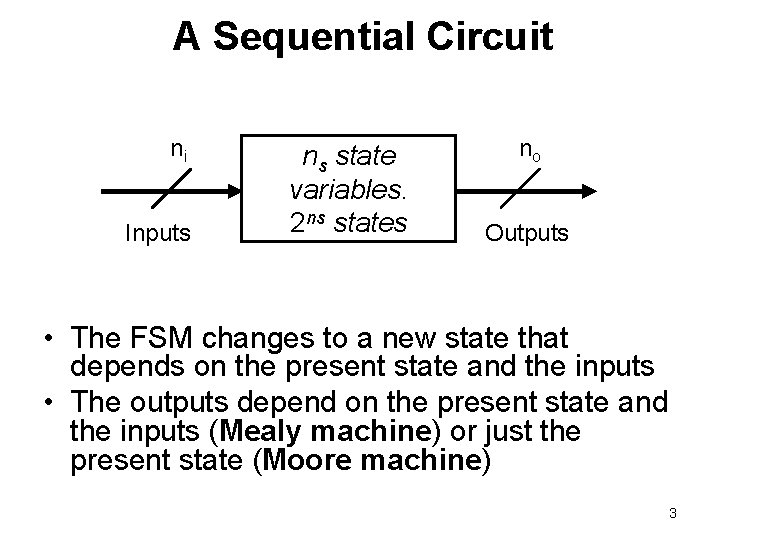
A Sequential Circuit ni Inputs ns state variables. 2 ns states no Outputs • The FSM changes to a new state that depends on the present state and the inputs • The outputs depend on the present state and the inputs (Mealy machine) or just the present state (Moore machine) 3

Finite State Machine State variables are binary values, corresponding to certain logic signals in the circuit. A circuit with ns binary state variables has 2 ns possible states. As large as it might be, 2 ns is always finite, so sequential circuits are sometime called finite-state machines.

Finite-State Machines • A generalised sequential logic system has a number of inputs (ni), and a number of outputs (no) which depend on the present, and past, values of the inputs • Sequential logic systems are normally formalised as finite-state machines (FSMs) • This does not impose limitations on the systems • FSMs are considered to have a number of internal states, each state being determined by some combination of values of the ns state variables 5

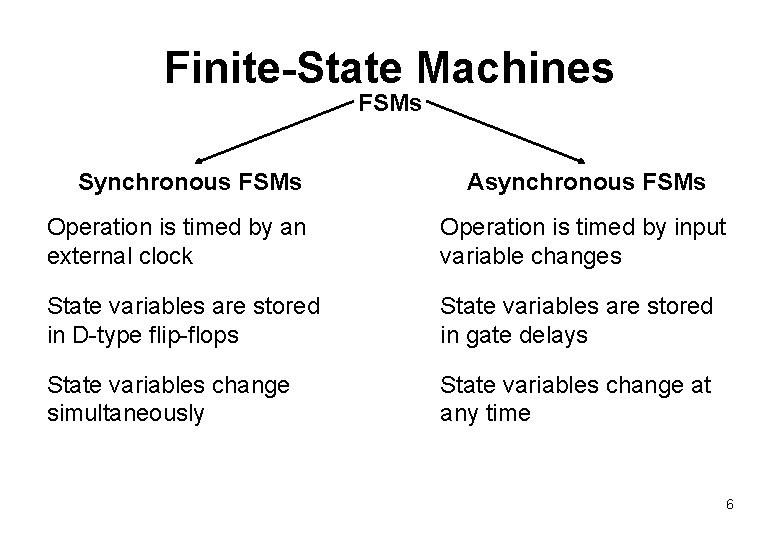
Finite-State Machines FSMs Synchronous FSMs Asynchronous FSMs Operation is timed by an external clock Operation is timed by input variable changes State variables are stored in D-type flip-flops State variables are stored in gate delays State variables change simultaneously State variables change at any time 6

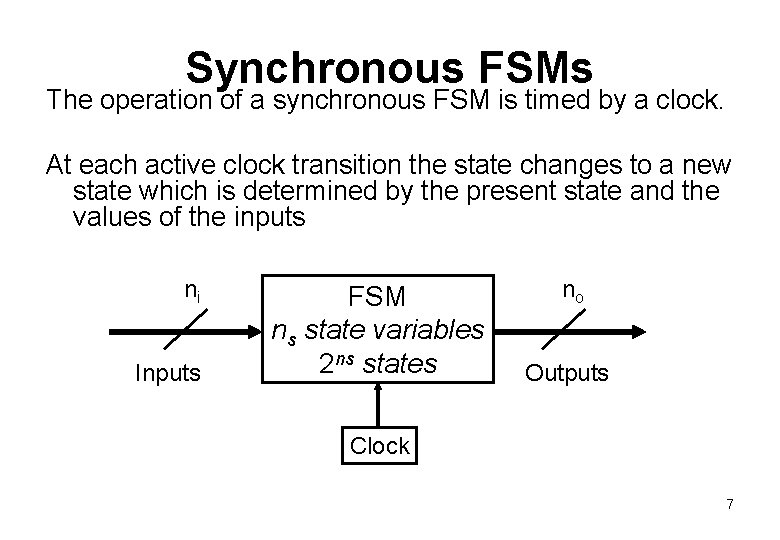
Synchronous FSMs The operation of a synchronous FSM is timed by a clock. At each active clock transition the state changes to a new state which is determined by the present state and the values of the inputs ni Inputs FSM ns state variables 2 ns states no Outputs Clock 7

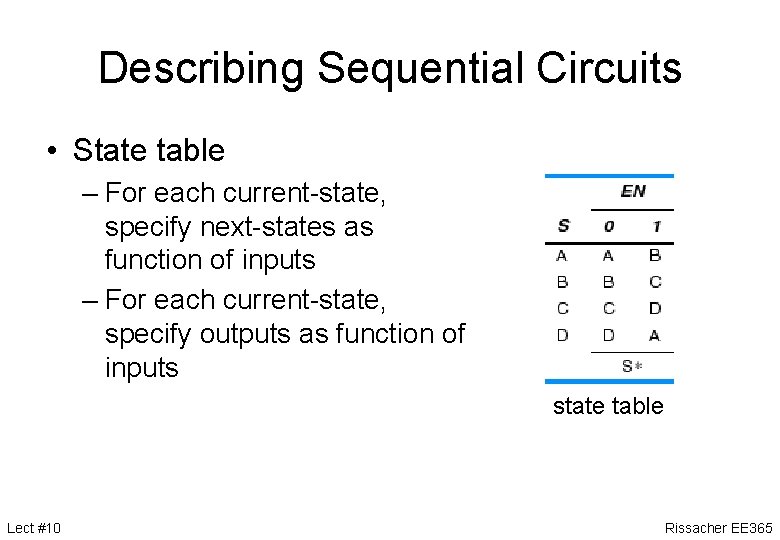
Describing Sequential Circuits • State table – For each current-state, specify next-states as function of inputs – For each current-state, specify outputs as function of inputs state table Lect #10 Rissacher EE 365

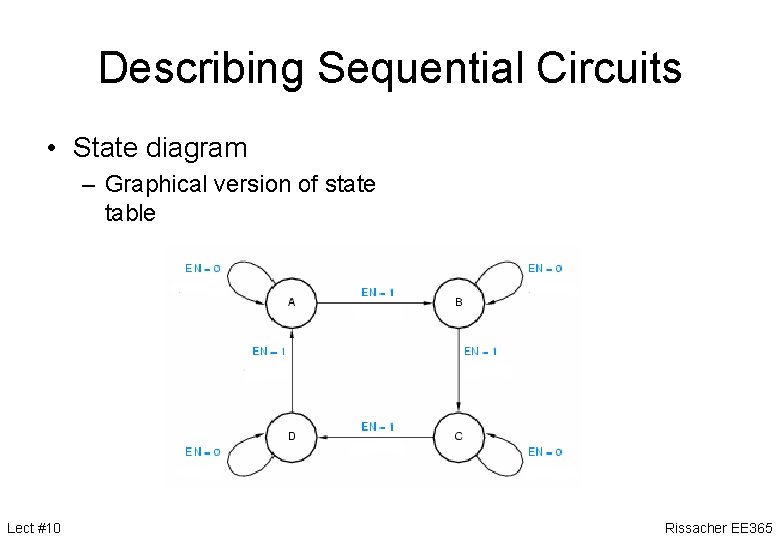
Describing Sequential Circuits • State diagram – Graphical version of state table Lect #10 Rissacher EE 365

Classifcation Sequential circuits can be classified into the following two categories: • Feedback sequential circuits • Clocked synchronous state machines A feedback sequential circuit uses ordinary gates and feedback loops to obtain memory in a logic circuit, thereby creating sequential circuit building blocks such as latches and flip-flops that are used in higher level designs. A clocked synchronous state machine uses these building blocks, to create circuits whose inputs are examined and whose outputs change in accordance with a controlling clock signal.

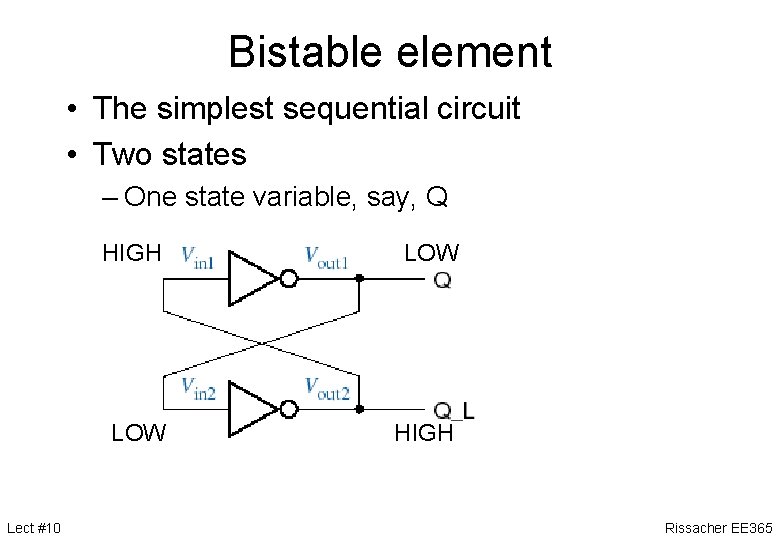
Bistable element • The simplest sequential circuit • Two states – One state variable, say, Q Lect #10 HIGH LOW HIGH Rissacher EE 365

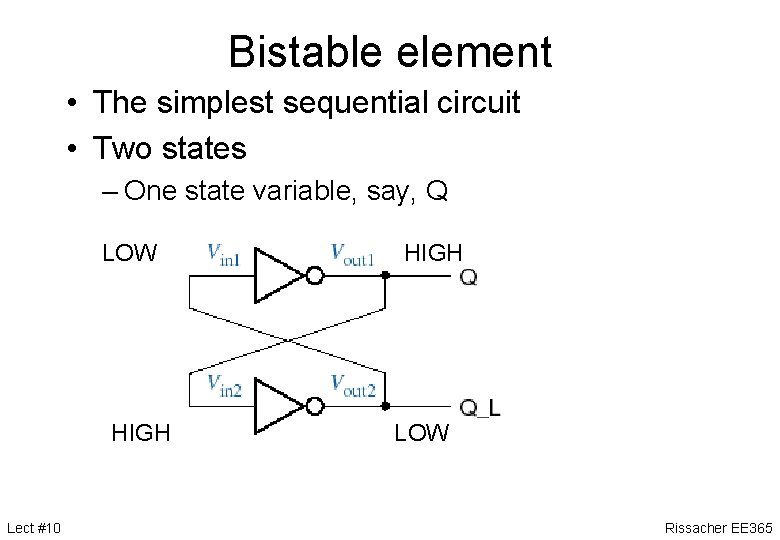
Bistable element • The simplest sequential circuit • Two states – One state variable, say, Q LOW HIGH Lect #10 HIGH LOW Rissacher EE 365

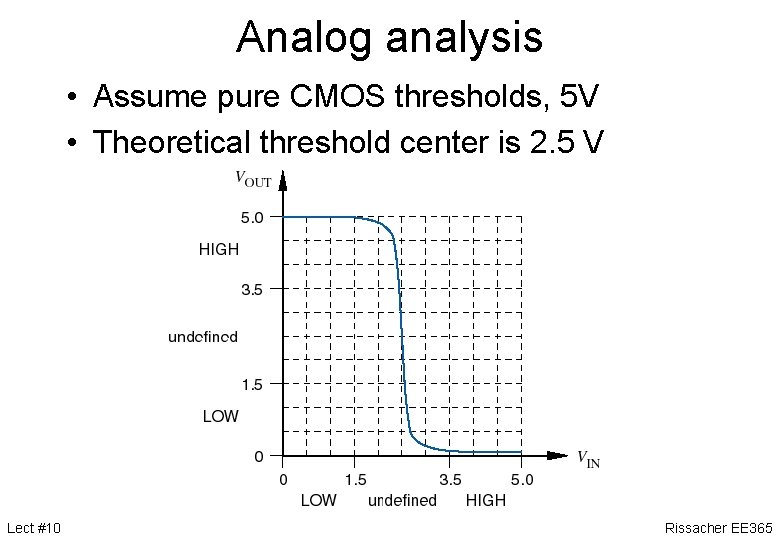
Analog analysis • Assume pure CMOS thresholds, 5 V • Theoretical threshold center is 2. 5 V Lect #10 Rissacher EE 365

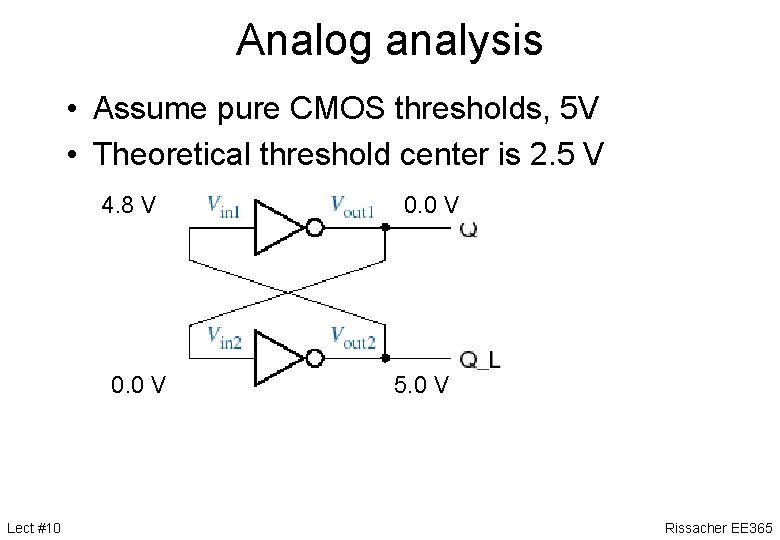
Analog analysis • Assume pure CMOS thresholds, 5 V • Theoretical threshold center is 2. 5 V 2. 5 4. 8 2. 51 VV 2. 5 V 0. 0 2. 0 Lect #10 2. 5 V 2. 0 0. 0 4. 8 5. 0 2. 5 V Rissacher EE 365

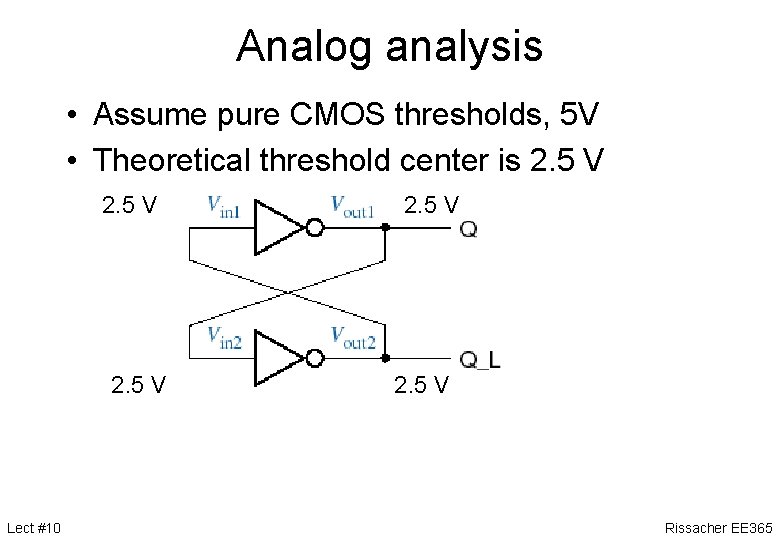
Analog analysis • Assume pure CMOS thresholds, 5 V • Theoretical threshold center is 2. 5 V Lect #10 2. 5 V Rissacher EE 365

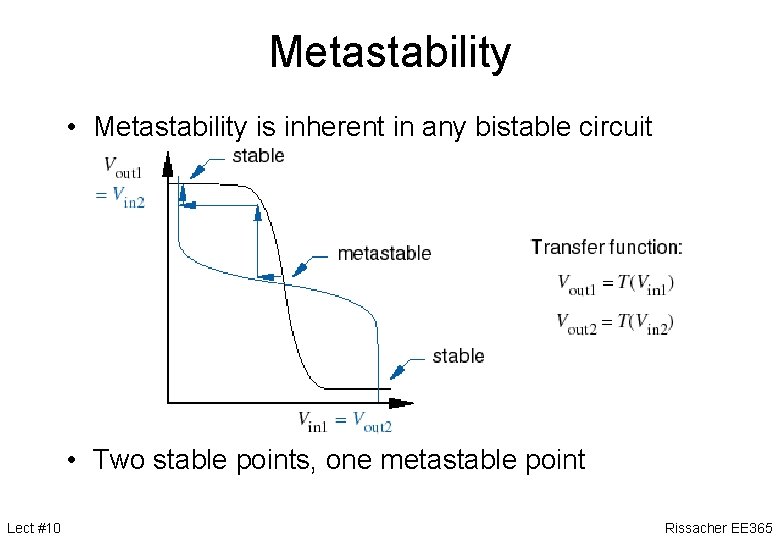
Metastability • Metastability is inherent in any bistable circuit • Two stable points, one metastable point Lect #10 Rissacher EE 365

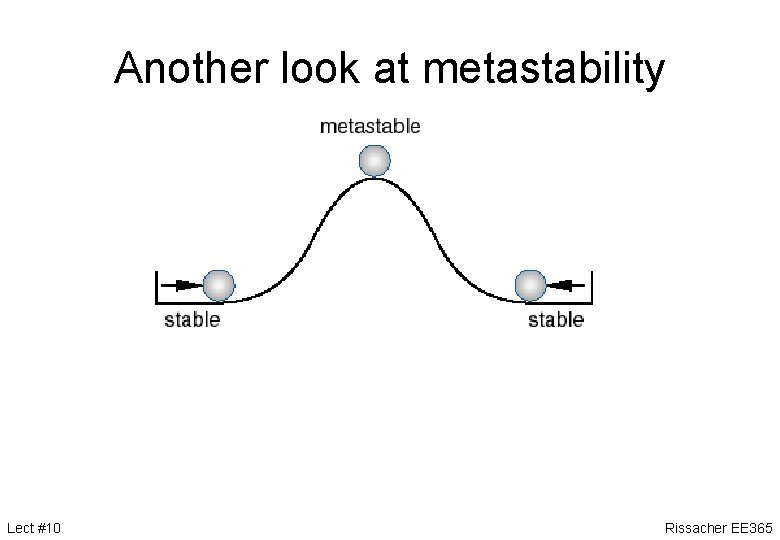
Another look at metastability Lect #10 Rissacher EE 365

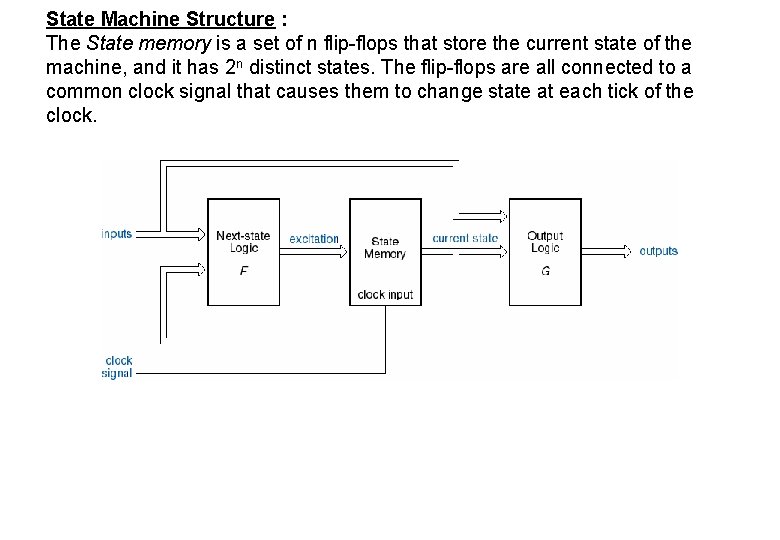
State Machine Structure : The State memory is a set of n flip-flops that store the current state of the machine, and it has 2 n distinct states. The flip-flops are all connected to a common clock signal that causes them to change state at each tick of the clock.

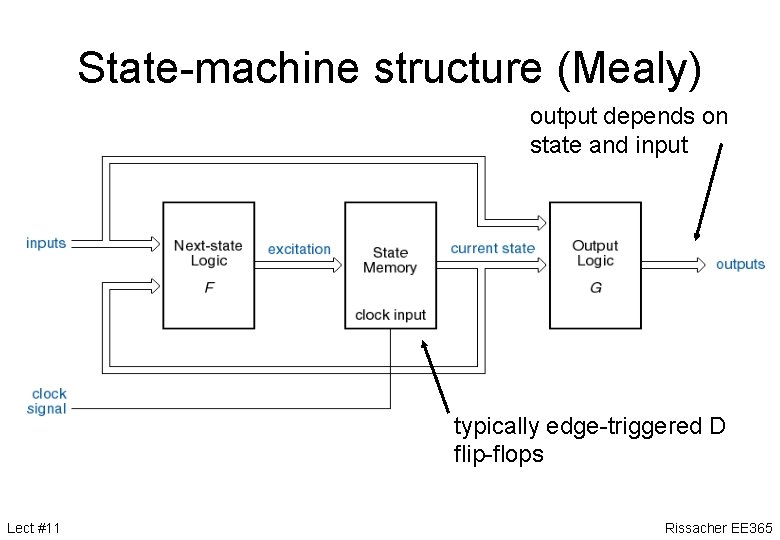
State-machine structure (Mealy) output depends on state and input typically edge-triggered D flip-flops Lect #11 Rissacher EE 365

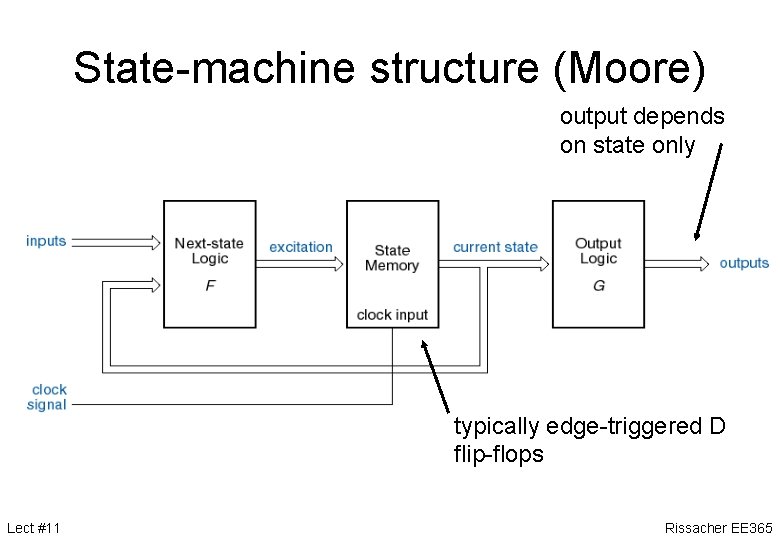
State-machine structure (Moore) output depends on state only typically edge-triggered D flip-flops Lect #11 Rissacher EE 365

Remember Mealy state and input Moore state Lect #11 Rissacher EE 365

Output-coded state assignment : It is often necessary to ensure that state-machine outputs are available as early as possible and do not change during each clock period. One way to get this behaviour is to encode the state so that the state variables themselves serve as outputs. We call this an output-coded state assignment. It produces a Moore machine in which the output logic consists of just wires.

Pipelined outputs : There is another approach for designing state machines in which the outputs during one clock period depend on the state and inputs during the previous clock period. We call these outputs as pipelined outputs and they are obtained by attaching another stage of memory to a Mealy machine’s outputs

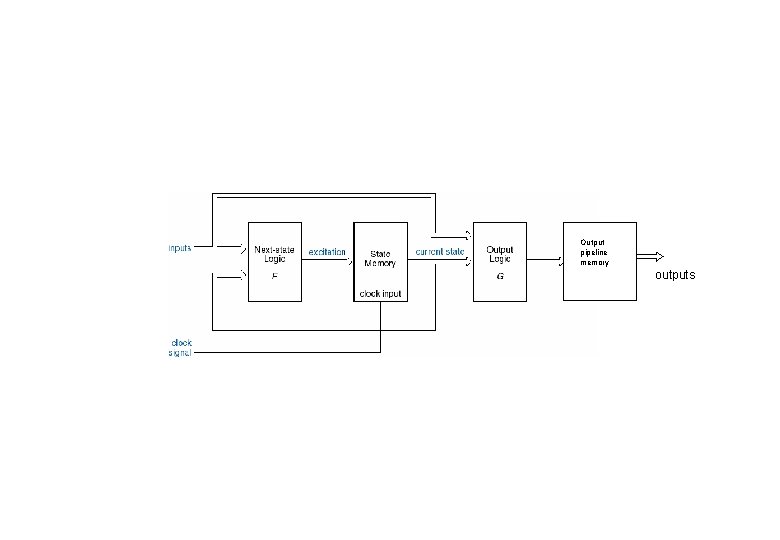
Output pipeline memory outputs

Notation, characteristic equations • Q means “the next value of Q. ” • “Excitation” is the input applied to a device that determines the next state. • “Characteristic equation” specifies the next state of a device as a function of its excitation. • S-R latch: Q = S + R´ · Q • Edge-triggered D flip-flop: Q = D Lect #11 Rissacher EE 365

State-machine analysis steps 1. Determine next-state function F and output function G. 2 a. Construct state table – For each state/input combination, determine the excitation value. – Using the characteristic equation, determine the corresponding next-state values (trivial with D f-f’s). 2 b. Construct output table – For each state/input combination, determine the output value. (Can be combined with state table. ) 3. (Optional) Draw state diagram Lect #11 Rissacher EE 365

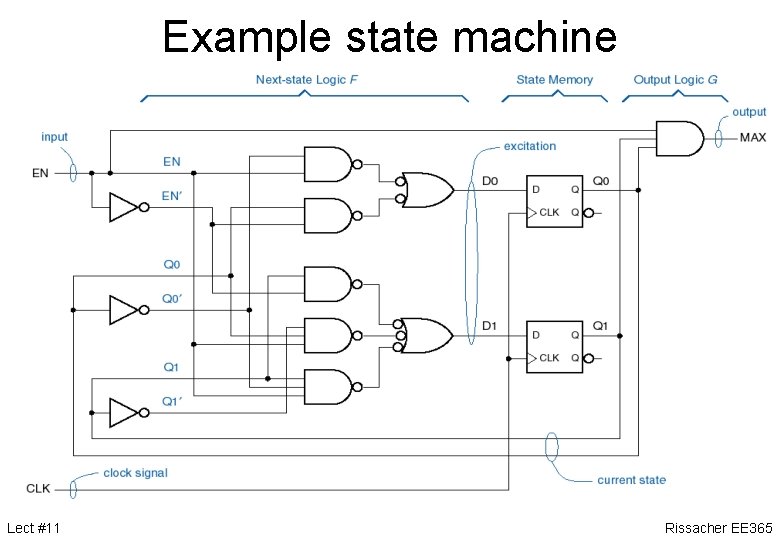
Example state machine Lect #11 Rissacher EE 365

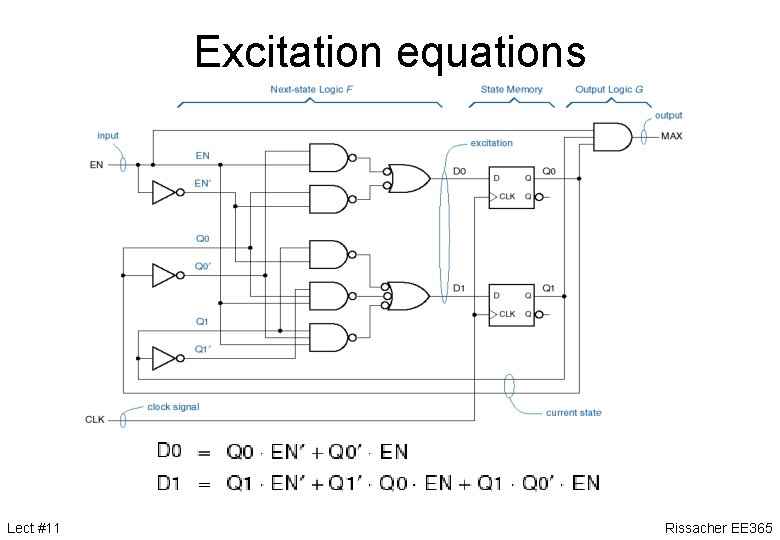
Excitation equations Lect #11 Rissacher EE 365

Transition equations • Excitation equations • Characteristic equations (D flip-flop is easy) • Substitute excitation equations into characteristic equations Lect #11 Rissacher EE 365

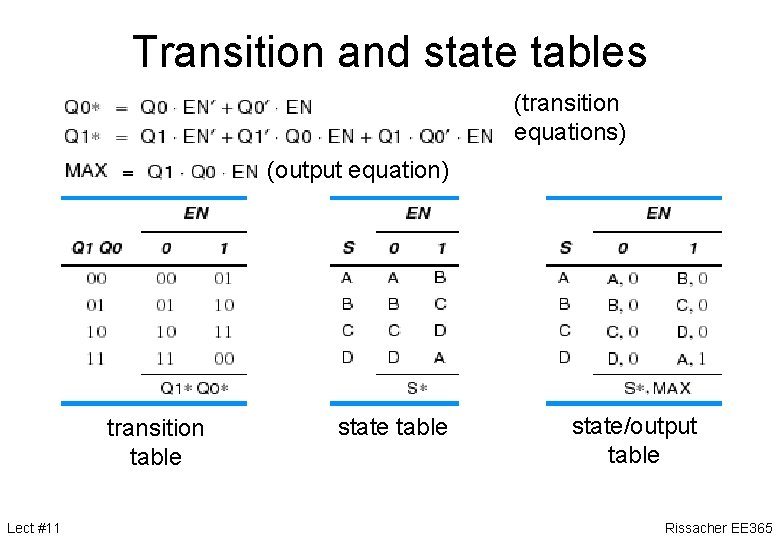
Transition and state tables (transition equations) (output equation) transition table Lect #11 state table state/output table Rissacher EE 365

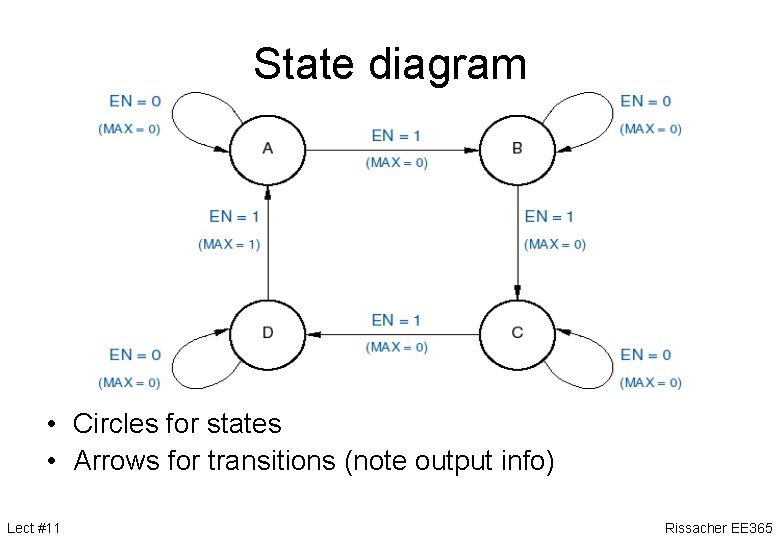
State diagram • Circles for states • Arrows for transitions (note output info) Lect #11 Rissacher EE 365