Topic Scan Conversion CSE 5280 Computer Graphics 112000

Topic >>>> Scan Conversion CSE 5280 - Computer Graphics 1/1/2000 1

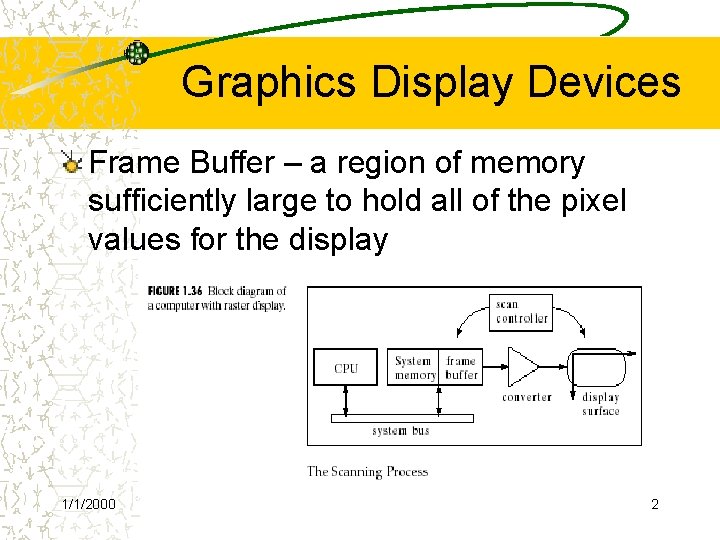
Graphics Display Devices Frame Buffer – a region of memory sufficiently large to hold all of the pixel values for the display 1/1/2000 2

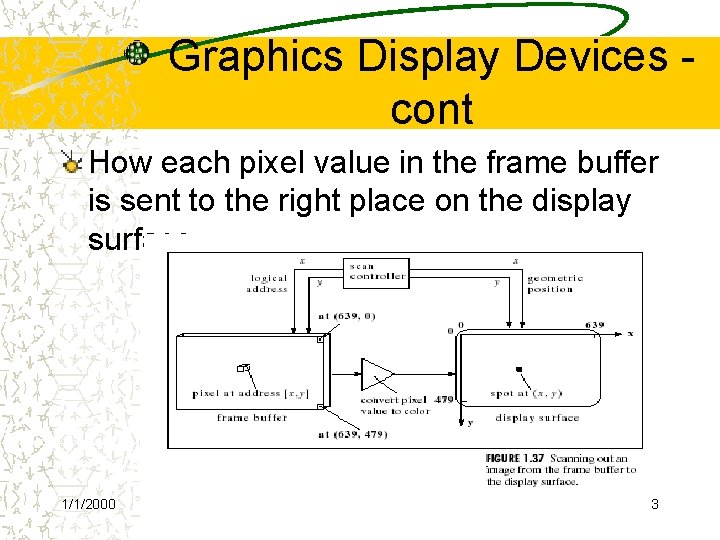
Graphics Display Devices cont How each pixel value in the frame buffer is sent to the right place on the display surface 1/1/2000 3

Graphics Devices – cont Each pixel has a 2 D address (x, y) ü For each address (x, y) there is a specific memory location that holds the value of the pixel (I. e. mem[136][252]) ü The scan controller sends the logical address (136, 252) to the frame buffer, which emits the value mem[136][252] ü The value mem[136][252] is converted to a corresponding intensity or color in the conversion circuit, and that intensity or color is sent to the proper physical position, (136, 252), on the display 1/1/2000 surface 4

Scan Converting Lines Line Drawing üDraw a line on a raster screen between 2 points üWhat’s wrong with the statement of the problem? 1/1/2000 • It does not say anything about which pts are allowed as end pts • It does not give a clear meaning to “draw” • It does not say what constitutes a “line” in the raster world • It does not say how to measure the success of 5

Scan Converting Lines cont Problem Statement üGiven 2 points P and Q in the plane, both with integer coordinates, determine which pixels on a raster screen should be “on” in order to make a picture of a unit-width line segment starting at point P and ending at point Q 1/1/2000 6

Finding the next pixel Special Case: ü Horizontal Line: • Draw pixel P and increment the x coordinate value by one to get the next pixel. ü Vertical Line: • Draw the pixel P and increment the y coordinate value by one to get the next pixel ü Diagonal Line: • Draw the pixel P and increment both the x and y coordinate values by one to get the next pixel ü What should we use in the general case? 1/1/2000 7

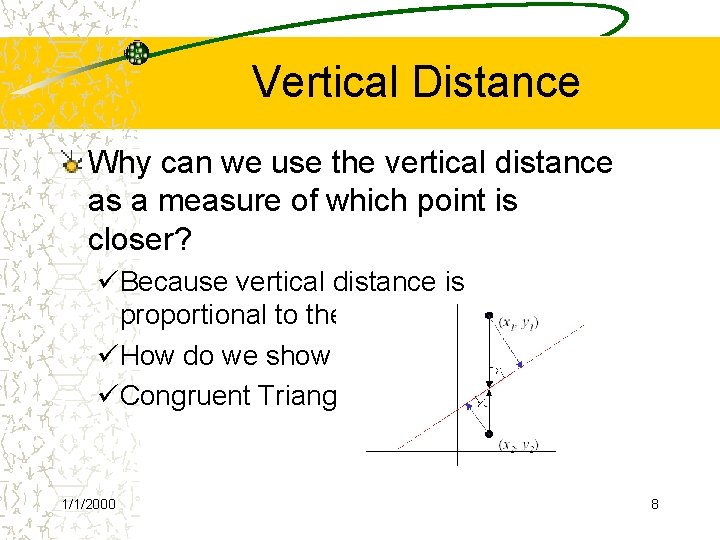
Vertical Distance Why can we use the vertical distance as a measure of which point is closer? üBecause vertical distance is proportional to the actual distance üHow do we show this? üCongruent Triangles 1/1/2000 8

Vertical Distance – cont By similar triangles we can see that the true distances to the line (in blue) are directly proportional to the vertical distances to the line (in black) for each point. Therefore the point with the smaller vertical distance to the line is the closest to the line 1/1/2000 9

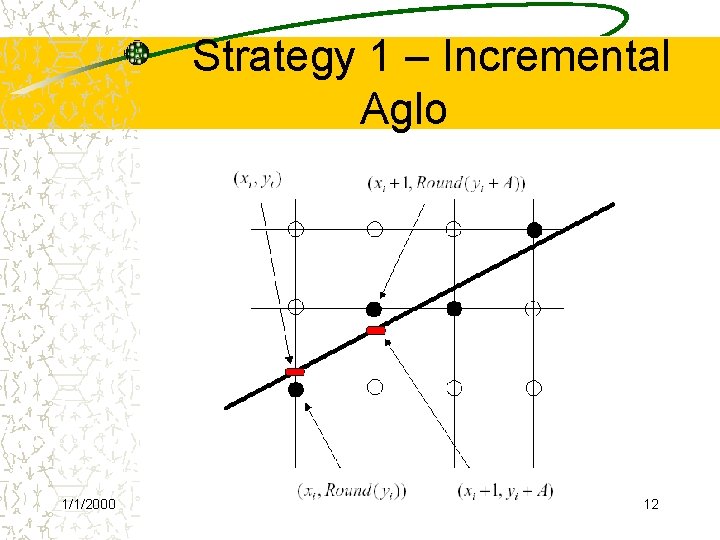
Strategy 1 – Incremental Algorithm The Basic Algorithm üFind the equation of the line that connects the 2 points P and Q üStarting with the leftmost point P, increment by 1 to calculate where A = slope, and B = y intercept üIntensify the pixel at üThis computation selects the closest pixel, the pixel whose distance to the “true” line 1/1/2000 is smallest 10

Strategy 1 – Incremental Algorithm The Incremental Algorithm üEach iteration requires a floating-point multiplication therefore, modify üIf , then üThus, a unit change in x changes y by slope A, which is the slope of the line üAt each step, we make incremental calculations based on the preceding step to find the next y value 1/1/2000 11

Strategy 1 – Incremental Aglo 1/1/2000 12

Example Code 1/1/2000 13

Problem with the Incremental Algorithm Rounding integers takes time Real variables have limited precision, summing an inexact slope (A) repetitively introduces a cumulative error buildup Variables y and A must be a real or fractional binary because the slope is a fraction üSpecial case needed for vertical lines 1/1/2000 14

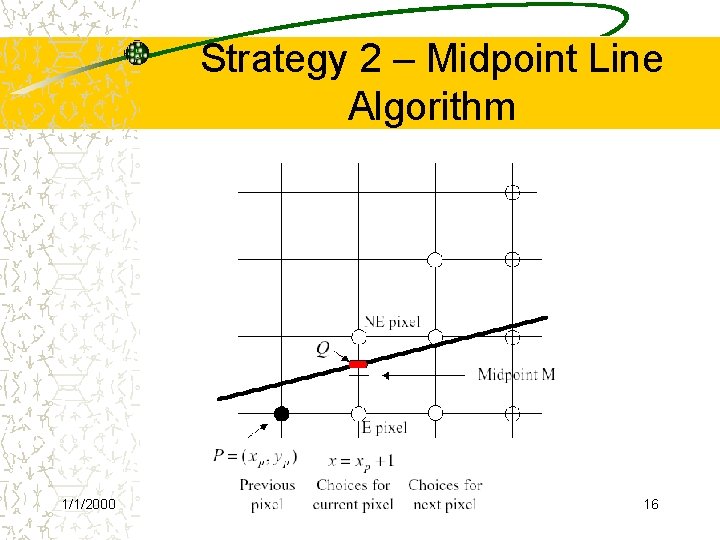
Strategy 2 – Midpoint Line Algorithm Assume that the line’s slope is shallow and positive ( 0 < slope < 1); other slopes can be handled by suitable reflections about the principle axes Call the lower left endpoint and the upper right endpoint Assume that we have just selected the pixel P at Next, we must choose between the pixel to the right (pixel E), or one right and one up (pixel NE) Let Q be the intersection point of the line 1/1/2000 15 being scan-converted with the grid line

Strategy 2 – Midpoint Line Algorithm 1/1/2000 16

Strategy 2 – Midpoint Line Algorithm The line passes between E and NE The point that is closer to the intersection point Q must be chosen Observe on which side of the line the midpoint M lies: ü E is closer to the line if the midpoint lies above the line (I. e. the line crosses the bottom half) ü NE is closer to the line if the midpoint lies below the line, I. e. , the line crosses the top half The error, the vertical distance between the chosen pixel and the actual line is always <= ½ The algorithm chooses NE as the next pixel for the line shown 1/1/2000 17 Now, find a way to calculate on which side of the

The Line The line equation as a function f(x): ü f(x) = A*x + B = dy/dx * x + B Line equation as an implicit function: ü F(x, y) = a * x + b * y + c = 0 for coefficients a, b, c where a, b != 0; from above, y *dx = dy*x + B*dx, so a = dy, b = -dx, c=B *dx, a>0 for y(0) < y(1) Properties (proof by the case analysis): ü when any point M is on the line ü when any point M is above the line ü when any point M is below the line 1/1/2000 18 ü Our decision will be based on the value of the

Decision Variable d: ü We only need the sign of to see where the line lies, and then pick the nearest pixel ü • If d > 0 choose pixel NE • If d < 0 choose pixel E • If d = 0 choose either one consistently How to update d: ü On the basis of picking E or NE, figure out the location of the M for that pixel, and the corresponding value of d for the next grid line 1/1/2000 19

Example Code 1/1/2000 20

Scan Conversion Summary 1/1/2000 21