Topic Radical Expressions Essential Question How are radical


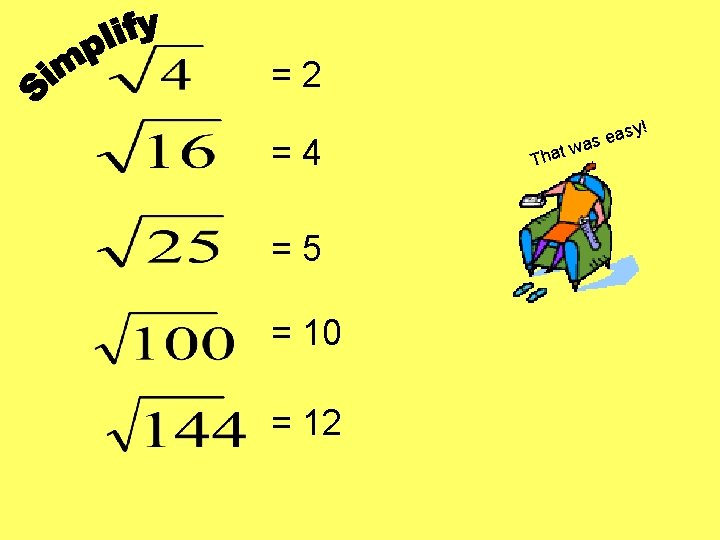
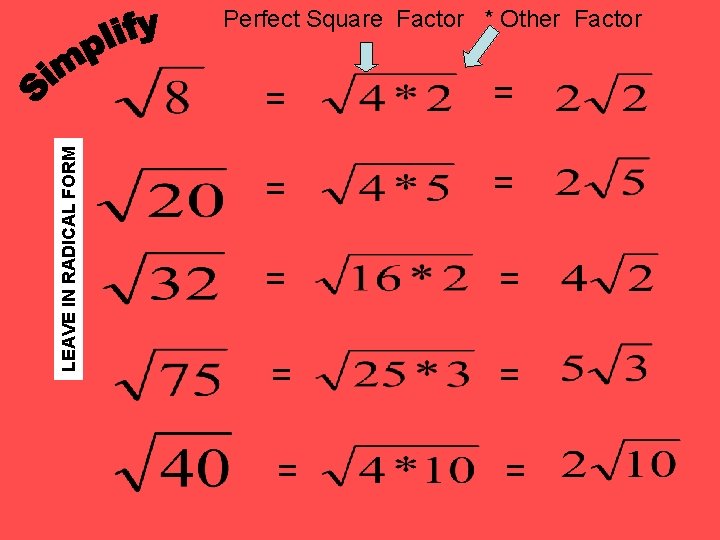





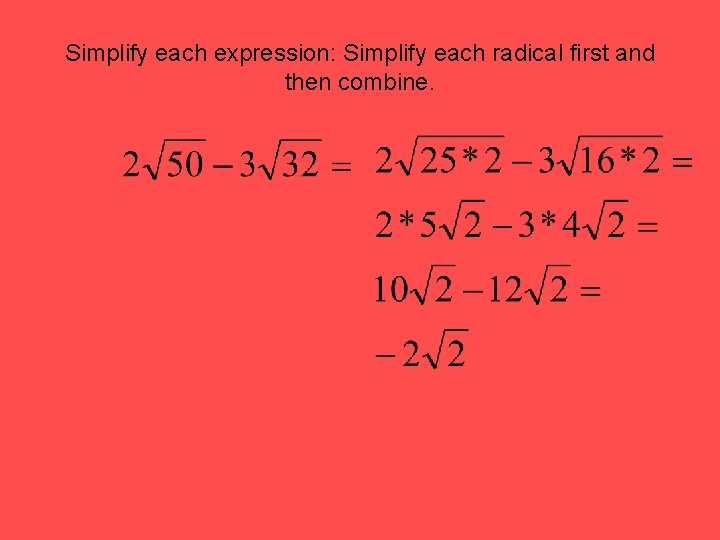
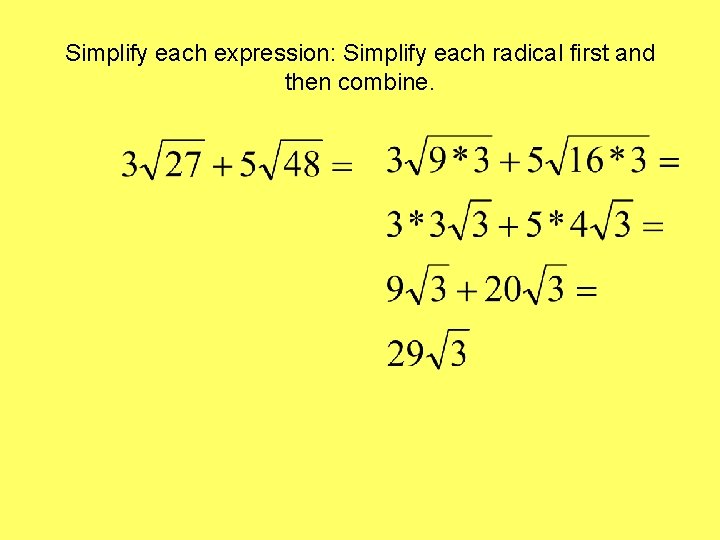
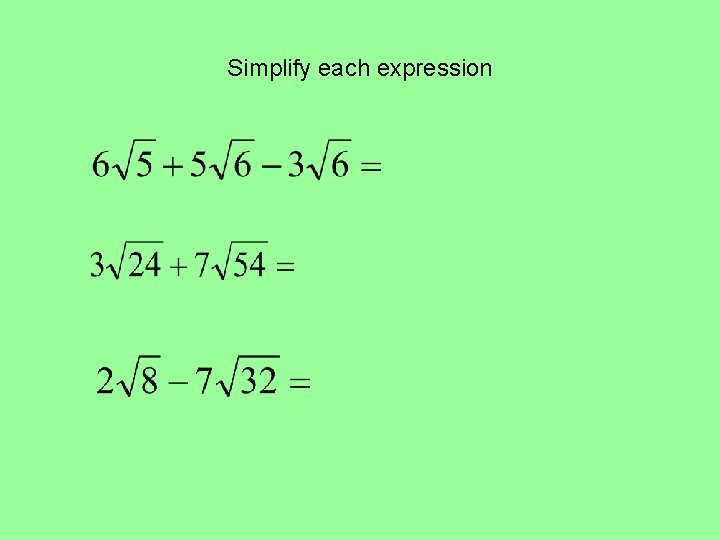
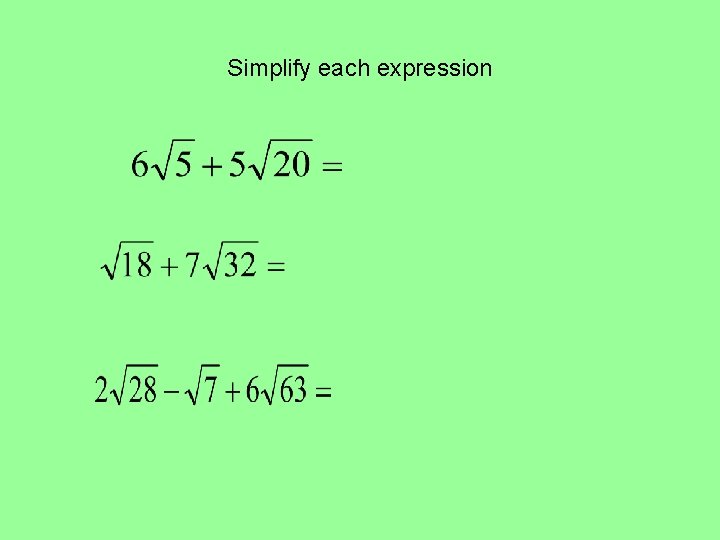










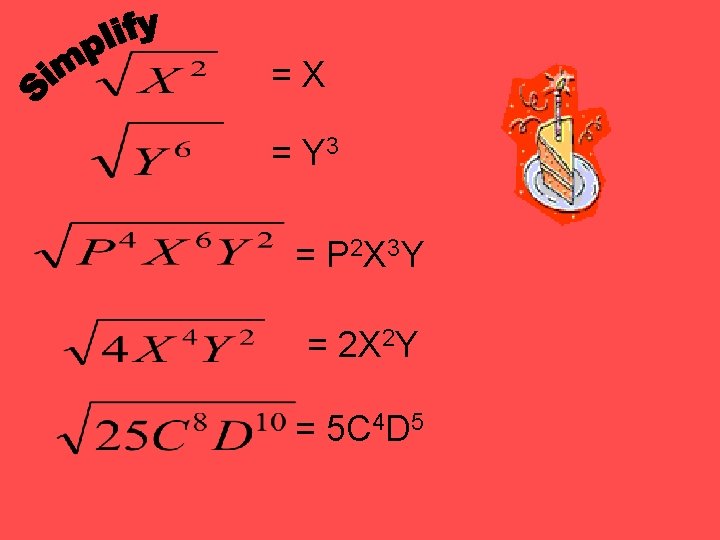

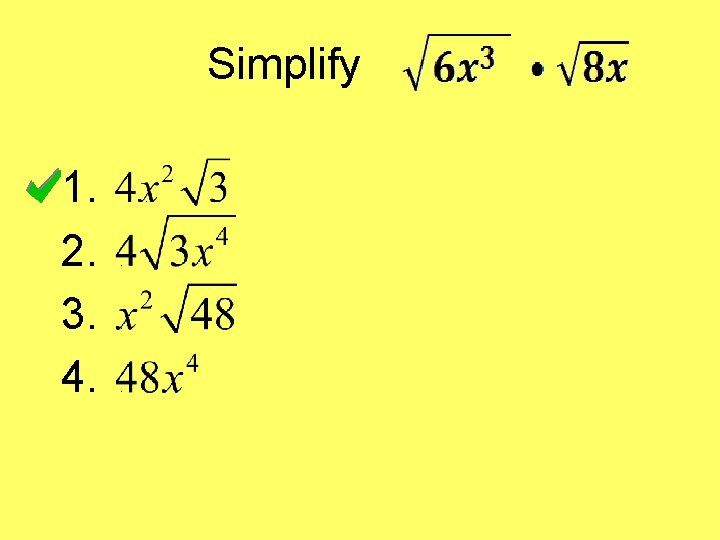
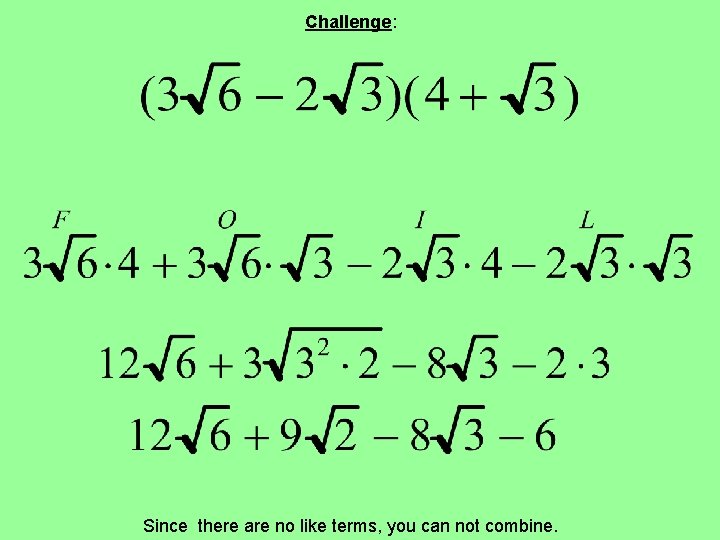

- Slides: 30

Topic: Radical Expressions Essential Question: How are radical expressions represented and how can you solve them? Simplifying Radicals

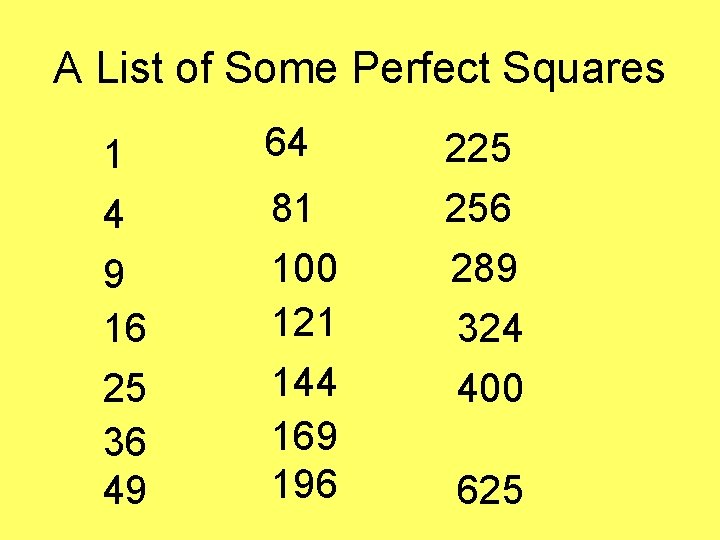
What numbers are perfect squares? 1 • 1 = 1 2 • 2 = 4 3 • 3 = 9 4 • 4 = 16 5 • 5 = 25 6 • 6 = 36 49, 64, 81, 100, 121, 144, . . .

A List of Some Perfect Squares 1 4 9 16 25 36 49 64 225 81 100 121 144 169 196 256 289 324 400 625
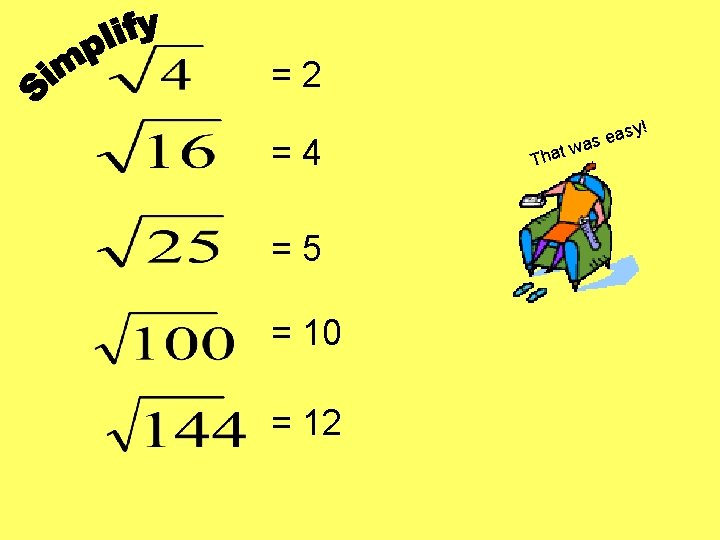
= 2 = 4 = 5 = 10 = 12 Tha t w y! s a e as
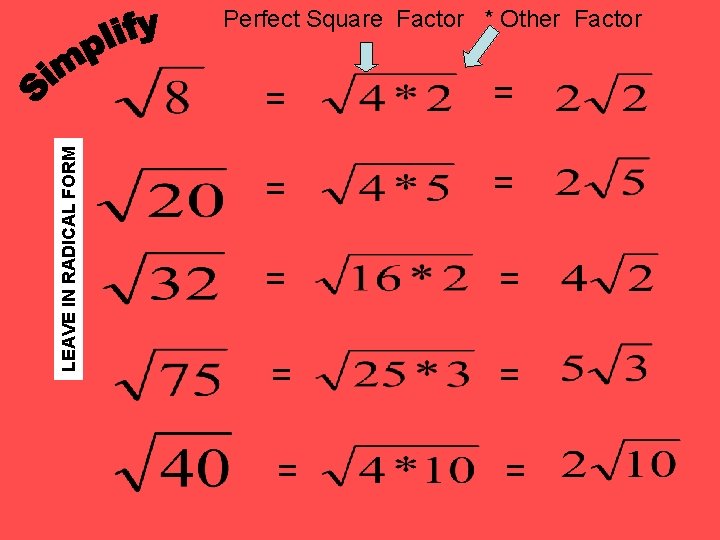
LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = = = =

LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = = = =

1. Simplify

Simplify 1. 2. 3. 4. . .

+ To combine radicals: combine the coefficients of like radicals Hint: In order to combine radicals they must be like terms

Simplify each expression
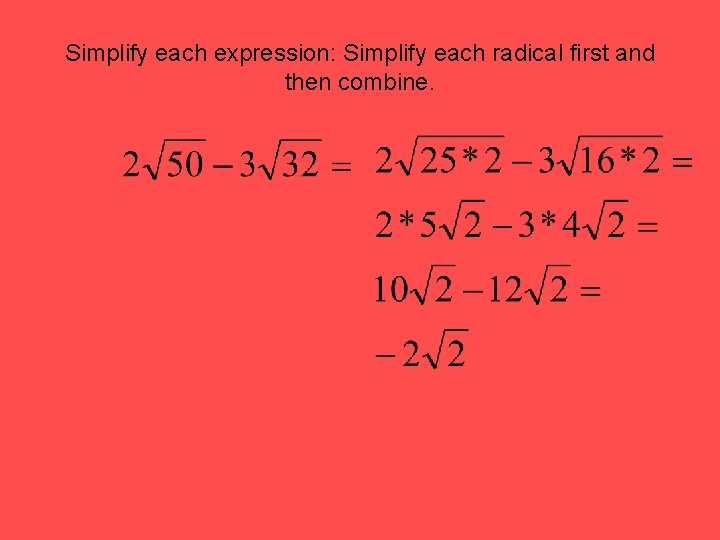
Simplify each expression: Simplify each radical first and then combine.
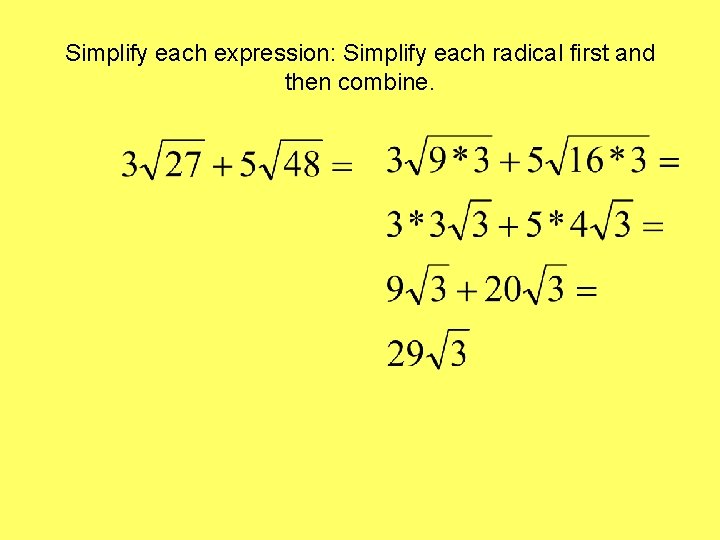
Simplify each expression: Simplify each radical first and then combine.
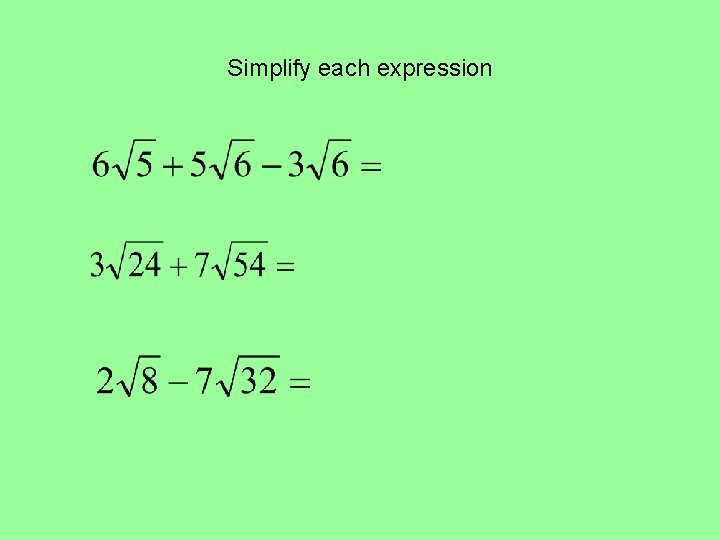
Simplify each expression
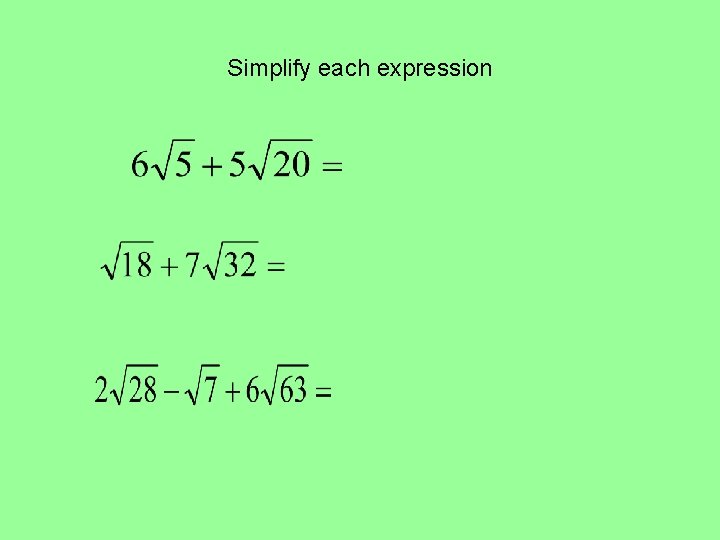
Simplify each expression

* To multiply radicals: multiply the coefficients and then multiply the radicands and then simplify the remaining radicals. Hint: to multiply radicals they DO NOT need to be like terms

Multiply and then simplify


To divide radicals: divide the coefficients, divide the radicands if possible, and rationalize the denominator so that no radical remains in the denominator


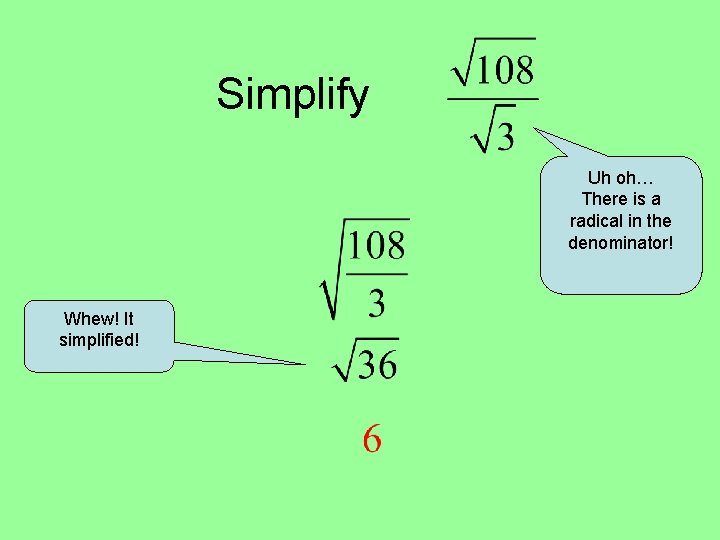
Simplify Uh oh… There is a radical in the denominator! Whew! It simplified!

Simplify Uh oh… Another radical in the denominator! Whew! It simplified again! I hope they all are like this!

This cannot be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator. 42 cannot be simplified, so we are finished.

Simplify Uh oh… There is a fraction in the radical! Since the fraction doesn’t reduce, split the radical up. How do I get rid of the radical in the denominator? Multiply by the “fancy one” to make the denominator a perfect square!

This can be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator.

This cannot be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator. Reduce the fraction.
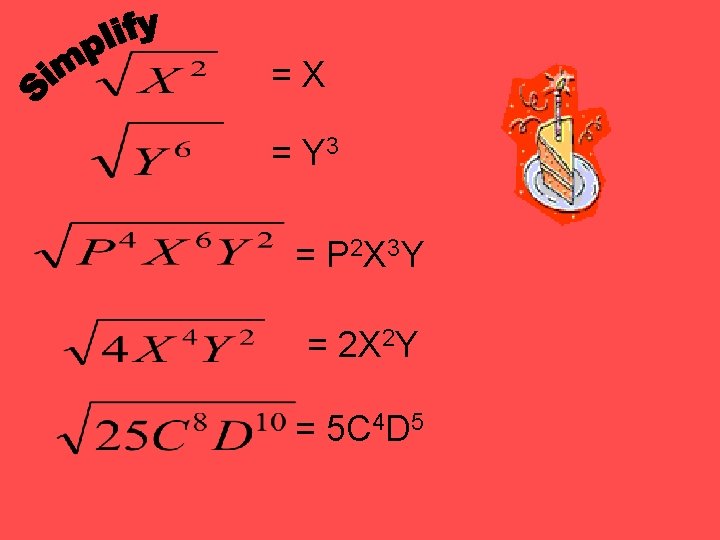
= X = Y 3 = P 2 X 3 Y = 2 X 2 Y = 5 C 4 D 5

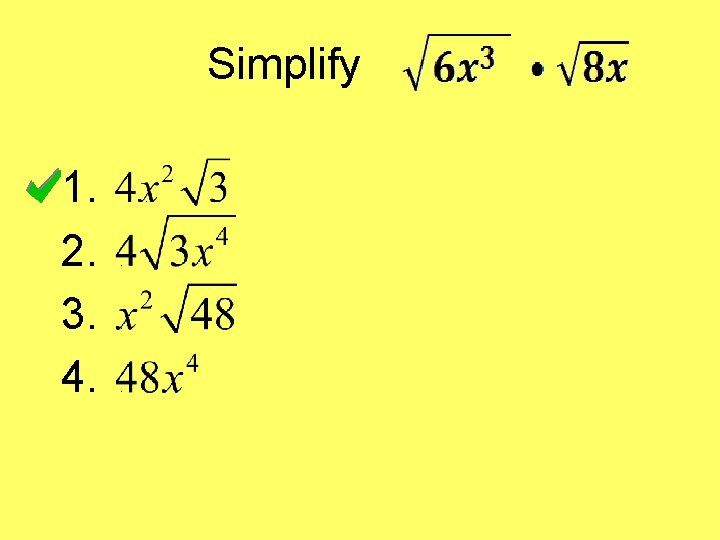
Simplify 1. 2. 3. 4. . .
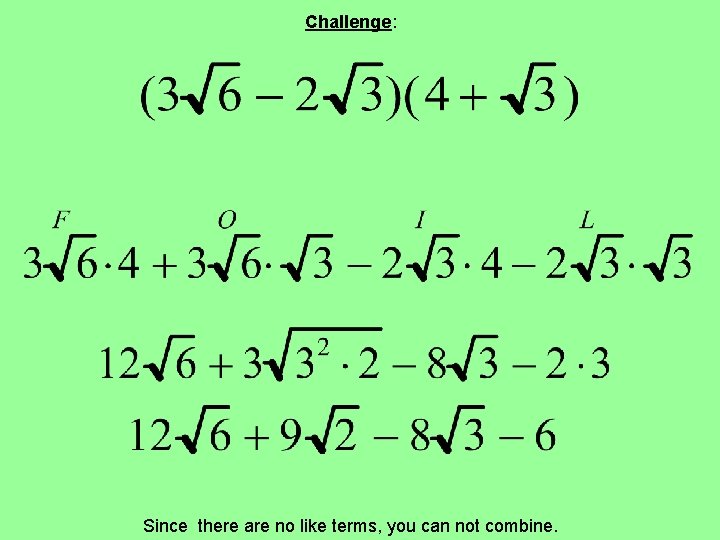
Challenge: Since there are no like terms, you can not combine.

How do you know when a radical problem is done? 1. No radicals can be simplified. Example: 2. There are no fractions in the radical. Example: 3. There are no radicals in the denominator. Example: