Topic 3 MSA Iterative Algorithms in Multiple Sequence

Topic 3: MSA Iterative Algorithms in Multiple Sequence Alignment Prepared By: 1. Chan Wei Luen 2. Lim Chee Chong 3. Poon Wei Koot 4. Xu Jin Mei 5. Yuan Ling 6. Zeng Sheng

Introduction n The introduction is MSA was given by the previous group, so we’ll not cover this here. n The major problem of progressive method is that alignments errors occurred during initial phase are propagated to the latter result. n Iterative method seeks to overcome this limitation by repeatedly realigned subgroups of the sequence and then by aligning these subgroup into a final sequence to achieve the best possible alignment.

Introduction. . In order to correct the mistakes introduced by the progressive alignment, iterative algorithm was introduced in 1987. n Barton suggested an algorithm that refines the alignment by realigning each sequence with the completed alignment less than that sequence. n For instance, sequence A 1 is aligned with the alignment of sequences A 2, A 3, … Ai , which was first removed any gaps that are common. n This process is repeated until all sequences have been realigned.

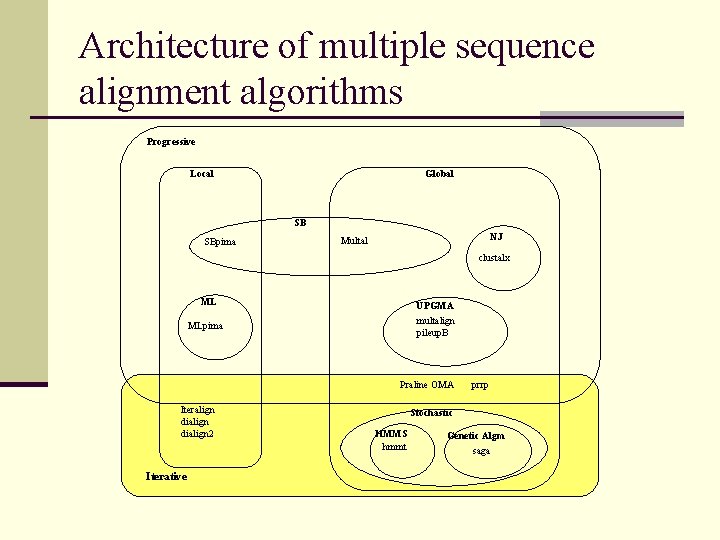
Architecture of multiple sequence alignment algorithms Progressive Global Local SB SBpima NJ Multal clustalx ML UPGMA multalign pileup. B MLpima Praline OMA Iteralign dialign 2 Iterative prrp Stochastic HMMS hmmt Genetic Algm saga

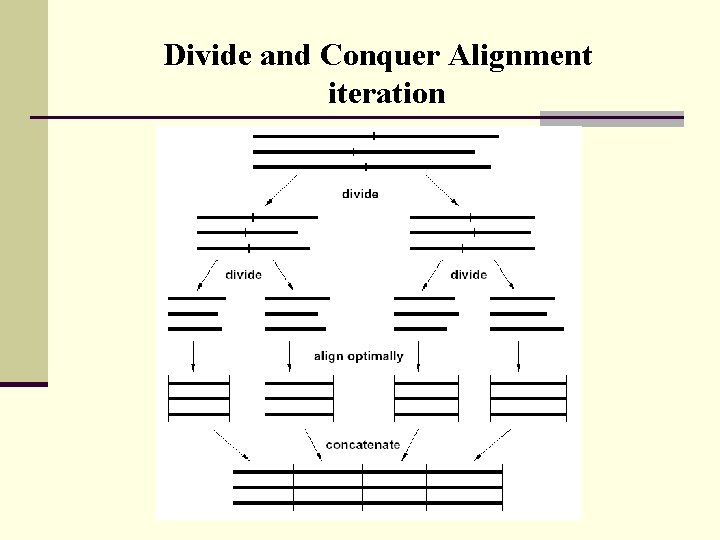
OMA n An iterative alignment algorithm n Using an improved algorithm for the optimal alignment of multiple biological sequences based on the A* algorithm n Using Divide and Conquer Alignment method (DCA) repeatedly

OMA Step 1) A small value of Z is used to divide the sequences Step 2 ) Align sub-sequences using A* algorithm and reassemble the alignment results Step 3 ) A larger value Z to divide the results of the previous alignments Step 4) Remove the inserts in divided sequences, align them and reassemble the alignment results Step 5 ) Repeat step 3 and 4 using increasing values of Z, up to optimality or you can stop at anytime.

Divide and Conquer Alignment iteration

Di. Align / Di. Align 2 n Background Ø New method for pairwise and multiple alignments Ø Di. Align and Di. Align 2 were proposed by Burkhard Morgenstern in 1998 and 1999 respectively Ø Di. Align 2 modified the weight function of Di. Align such that: it reduces the running time, ü it can be applied both globally and locally to related sequence sets ü

Di. Align / Di. Align 2 n Ø Ø Algorithm Step 1: All optimal pairwise alignments are formed and sorted v according to their weighted scores v according to the degree of overlap with other diagonals Step 2: The diagonal with the highest weight is the first one to be selected for the alignment.

Di. Align / Di. Align 2 Ø Step 3: The next diagonal from the list is checked for consistency and added to the alignment if consistent, and is repeated iteratively until no additional diagonals can be found. Ø Step 4: The program introduces gaps into the sequences until all residues connected by the selected diagonals are properly arranged.

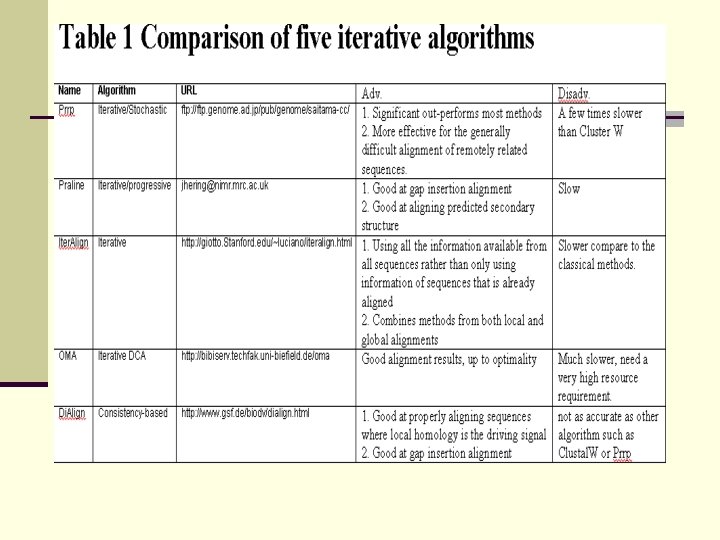
Di. Align / Di. Align 2 Ø Advantage n Good at properly aligning sequences where local homology is the driving signal. Ø Disadvantage n Not as accurate as other algorithm such as Clustal W or Prrp but it works well in sequences which require very long insertions to be properly aligned

Iteralign n Iteralign algorithm is as follows: n First, designate the r original sequences by {Si} n Each of this sequence is used to match all r sequences in an ungapped mode n Construct an “ameliorated” sequence for each of the sequences and call it {Sk(1)} n Align each of the original sequences Si to Sk(1) n Create a new ameliorated sequence {Sk(2)} n Iterate the process until no more change in the new ameliorated sequence {Sk(n)} n Call this final sequence Ck(1)

Iteralign n n Collect all Ck(1) sequences and call them {Ci(1)} set also known as consensus sequences or round 1 Use Ci(1) as the input to step 1 and repeat the whole process iteratively until there is no more change We call this final set the core blocks {Ci( )} Core blocks have the property that the consensus aligns maximally to all individual sequences Use a local Dynamic Programming (DP) method to optimize the displacements (allowing gap) of individual sequences

Iteralign

Open Issue n There are some strengths and weaknesses in iterative methods. n Pro: A common characteristic of these methods lies in that the accuracy of alignment has been markedly improved n Cons: n However, huge computational time and memory complexity is required. n n A multitude of parallel techniques have been proposed to solve this problem. However, parallelization of the iterative alignment algorithm remains a difficult task. n In summary, iterative alignment strategy is a promising trend.

Conclusion n Traditionally the most popular approach for multiple sequence alignment has been the progressively alignment method. n But over the years, Iterative alignment strategy will be a more suitable choice of multiple sequence alignment.