Topic 3 Data Binary Numbers Computer Science Number

Topic 3: Data Binary Numbers Computer Science

Number Systems “There are 10 types of people in the world: Those who understand binary, and those who don’t. ” • Do you understand the saying? 2 Data: Binary Numbers

Number Systems • As far as numbers go, we’re most used to denary • It’s the number system that uses 10 possible digits 0 to 9 • A number is made up of as many of these digits as needed 1 42 3 34 314159 Data: Binary Numbers

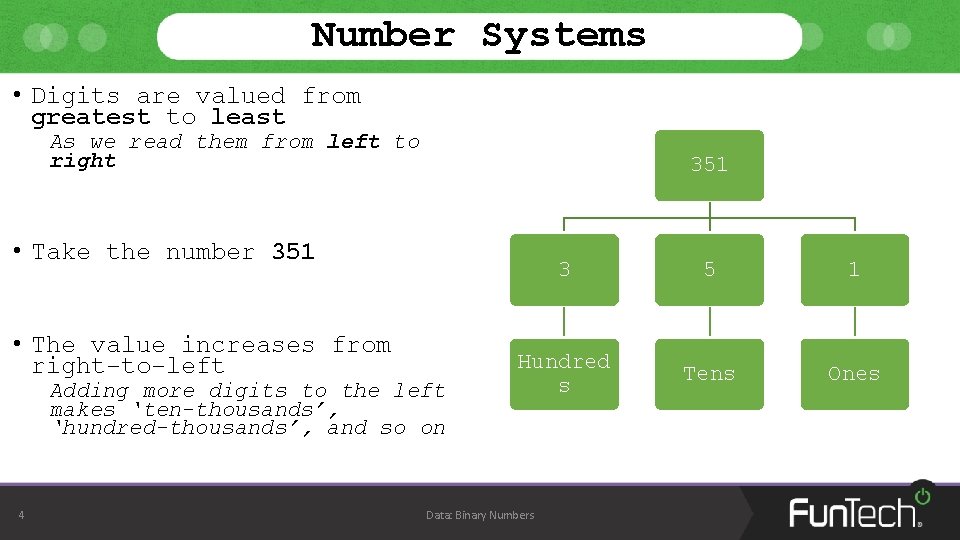
Number Systems • Digits are valued from greatest to least As we read them from left to right 351 • Take the number 351 • The value increases from right-to-left Adding more digits to the left makes ‘ten-thousands’, ‘hundred-thousands’, and so on 4 3 5 1 Hundred s Tens Ones Data: Binary Numbers

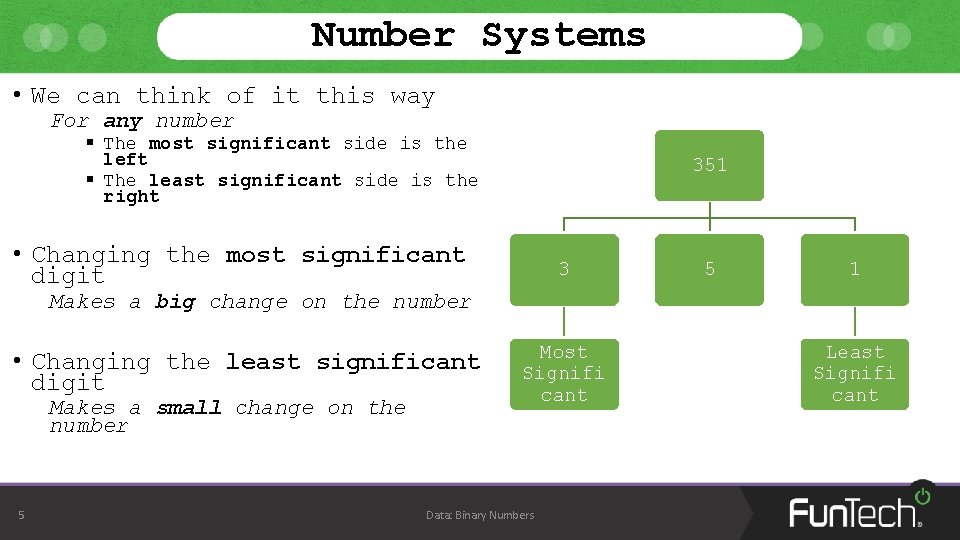
Number Systems • We can think of it this way For any number § The most significant side is the left § The least significant side is the right 351 • Changing the most significant digit 3 5 1 Makes a big change on the number • Changing the least significant digit Makes a small change on the number 5 Most Signifi cant Data: Binary Numbers Least Signifi cant

Number Systems • Every number system works off a base • Denary is in base 10 • That means every digit has 10 possible 0 to 9 The base appears near the bottom of values the number 35110 • Base 9 would have 9 possible values 0 to 8 • Base 4 would have 4 possible values 0 to 3 6 Data: Binary Numbers 0. 510

Number Systems • With any base, we can calculate the denary result 102 3 101 5 100 1 (3 x 102) + (5 x 101) + (1 x 100) = (3 x 100) + (5 x 10) + (1 x 1) = 300 + 50 + 1 = 351 • Each next significant digit is always the next power up of the base E. g. the least significant digit is always [base] 0 Then we have [base] 1 Most significant digit is [base] n - 1 where n is the number of digits • We multiply the digit’s worth by the digit • Finally, we add together each product to get the final result 7 Data: Binary Numbers

Number Systems • Calculating this result is a bit redundant in denary We already have the result • But this lets us convert other number systems to denary • Let’s look at another number system • Called binary 8 Data: Binary Numbers

Binary • The binary number system is a base 2 system Has 0 and 1 as possible digits • Here are some examples 00101 0 1101 1111111 1 000011011 11000011010101101 01010 • Still follows the same number system rules Digit on right is least significant Digit on left is most significant 9 Data: Binary Numbers

Binary • Let’s look at a number 23 1 22 20 0 1 21 0 (23 x 1) + (22 x 0) + (21 x 0) + (20 x 1) = (8 x 1) + (4 x 0) + (2 x 0) + (1 x 1) 2 = 8 + 0 + 1 = 9 • The number in binary is 1001 Can also be written as 10012 Let’s readers know its in base • Can calculate its denary value by doing the calculation from before Multiply the digit’s worth by the digit’s value 10 Data: Binary Numbers

• Calculate the denary value for each of these binary numbers 11 1101 0010 010101 001100 100000 1100001111 10001101 Data: Binary Numbers

Denary to Binary • Turning a number from one system into another is an example of conversion • The exercise made you convert from binary to denary • How about going the other way around? It’s not as simple But still easy to follow 12 Data: Binary Numbers

Denary to Binary • We start with a number • Then we find the largest power of 2 that fits in it Cannot be larger • We take this power away from the number Ending up with a result Starting number: Largest Power of 2: Take the power away: Mark that as a 1: Then look at next power: Take that power away: Marks that as a 1: And repeat the process… • We put a 1 in that digit on the binary number We put 0 if we can’t subtract it • We repeat this process, going down the powers Until we reach the end 26 2 5 2 4 2 3 2 2 2 1 2 0 1 1 • The end result is the binary version 13 End up with Data: Binary Numbers 103 64 (26) 103 – 64 = 59 26 -> 1 32 (25) 59 – 32 = 27 25 -> 1 27 – 16 = 11 24 -> 1 11 – 8 = 3 23 -> 1 3 – 4 (CAN’T DO) 22 -> 0 3– 2=1 21 -> 1 1– 1=0 20 -> 1

• Calculate the binary value for each of these denary numbers 14 15 7 3 78 64 80 102 125 255 Data: Binary Numbers

Binary in Computers • There’s a reason why binary is important • It’s used on computers every day • Computers are made up of electrical circuits • These circuits have two states: low voltage, and high voltage Seem familiar? • If there are only two states, we can represent a circuit using a single binary digit Low voltage: 0 High voltage: 1 15 Data: Binary Numbers

Binary in Computers • These voltages (and subsequent binary) are used for lots of things Data on computers § § Images Numbers Characters Video Memory addresses § Where things are stored on a computer • Using binary to store data (like text) is known as encoding Something we’ll be looking at this term 16 Data: Binary Numbers

Binary in Computers • Data on a computer has a very specific unit Bits Bit: 0 or 1 (single digit) Byte: 00110101 (8 bits) Word: 32/64 bits (depending on computer architecture) • Each digit in a binary number is a single bit • So, a 4 digit binary number has 4 bits • A group of 8 bits makes a single byte • Either 32 or 64 bits (depending on the computer architecture) makes a word 17 Data: Binary Numbers

Units of Data • Things on the computer can get pretty large Videos, for example, are typically larger than text documents • Showing their size in bytes would end up with very large numbers • Instead, we can use other units of measurement • There are two types for data Units representing powers of 2: kibibytes Units representing powers of 10: kilobytes 18 Data: Binary Numbers

Units of Data • In SI (International System of Units), we have base units Metres (m) Litres (l) Bytes (B) • We can represent larger values by adding prefixes kilo (103) kilobytes (k. B) mega (106) (MB) giga (109) gigabytes (GB) tera (1012) (TB) 19 kilometres (km) megametres (Mm) megalitres (Ml) gigametres (Gm) terametres (Tm) Data: Binary Numbers kilolitres (kl) megabytes gigalitres (Gl) teralitres (Tl) terabytes

Units of Data • So, we have 1 k. B = 1, 000 B 1 MB = 1, 000 k. B = 1, 000 B 1 GB = 1, 000 MB = 1, 000 k. B = 1, 000, 000 B 1 TB = 1, 000 GB = 1, 000 MB = 1, 000, 000 k. B = 1, 000, 000 B • However, binary works in base 2, not base 10 • So there’s a different set of units we can use 20 Data: Binary Numbers

Units of Data • We can use the ‘kibi’ equivalent of the prefixes kibibyte: Ki. B 1 Ki. B mebibyte: Mi. B 1 Mi. B gibibyte: Gi. B 1 Gi. B tebibyte: Ti. B 1, 099, 511, 627, 776 B = = 210 B = 210 Ki. B 210 Mi. B 210 Gi. B 1, 024 B = 220 B = 1, 048, 576 B = 220 Ki. B = 230 B = 1, 073, 741, 824 = 220 Mi. B = 230 Ki. B = 240 B = • These are more ‘accurate’ than the SI units, as these units work in base 2 • Historically, kilo has been used when kibi was actually meant In terms of hard-drive sizes 21 Data: Binary Numbers

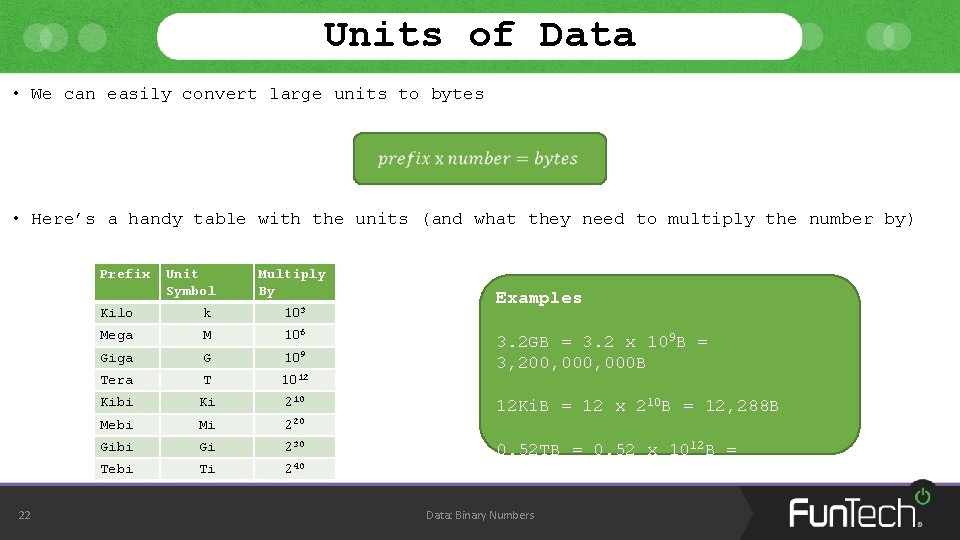
Units of Data • We can easily convert large units to bytes • Here’s a handy table with the units (and what they need to multiply the number by) Prefix 22 Unit Symbol Multiply By Kilo k 103 Mega M 106 Giga G 109 Tera T 1012 Kibi Ki 210 Mebi Mi 220 Gibi Gi 230 Tebi Ti 240 Examples 3. 2 GB = 3. 2 x 109 B = 3, 200, 000 B 12 Ki. B = 12 x 210 B = 12, 288 B 0. 52 TB = 0. 52 x 1012 B = 520, 000, 000 B Data: Binary Numbers

• Calculate the number of bytes for the following values 23 2 KB 1. 3 Ki. B 10 MB 0. 5 Gi. B 1. 2 TB 0. 2 Mi. B Data: Binary Numbers

Converting Between Units • We have two different sets of units • So we may be asked to convert from one unit to another MB to Mi. B Ki. B to GB Gi. B to MB • To go from one to the other, we always follow the same rule First find the number of bytes Then divide this by the prefix we’re moving to 24 Data: Binary Numbers

• Convert the following amounts of bytes to the requested unit 25 2 KB to Ki. B 4 Mi. B to MB 2. 5 Gi. B to GB 0. 2 MB to Ki. B 1. 2 TB to Gi. B 0. 2 Mi. B to KB Data: Binary Numbers