Topic 2 Multipressure Systems Ts diagram Standard VCRC

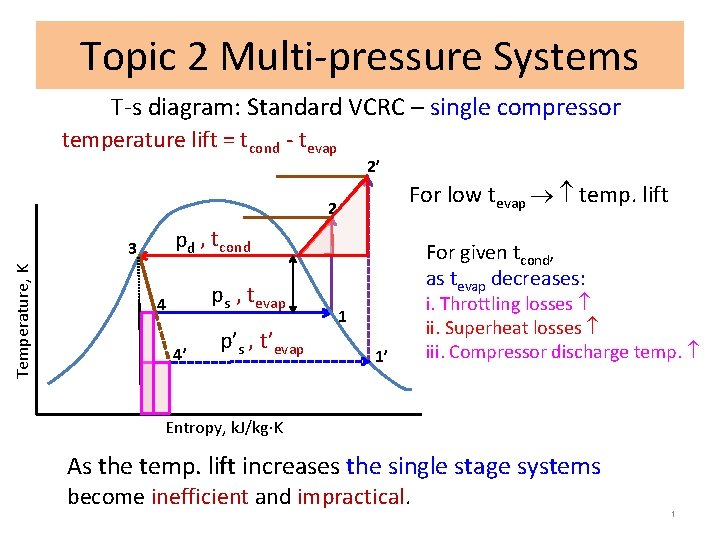
Topic 2 Multi-pressure Systems T-s diagram: Standard VCRC – single compressor temperature lift = tcond - tevap 2’ For low tevap temp. lift 2 pd , tcond Temperature, K 3 ps , tevap 4 4’ p’s , t’evap For given tcond, as tevap decreases: 1 1’ i. Throttling losses ii. Superheat losses iii. Compressor discharge temp. Entropy, k. J/kg K As the temp. lift increases the single stage systems become inefficient and impractical. 1

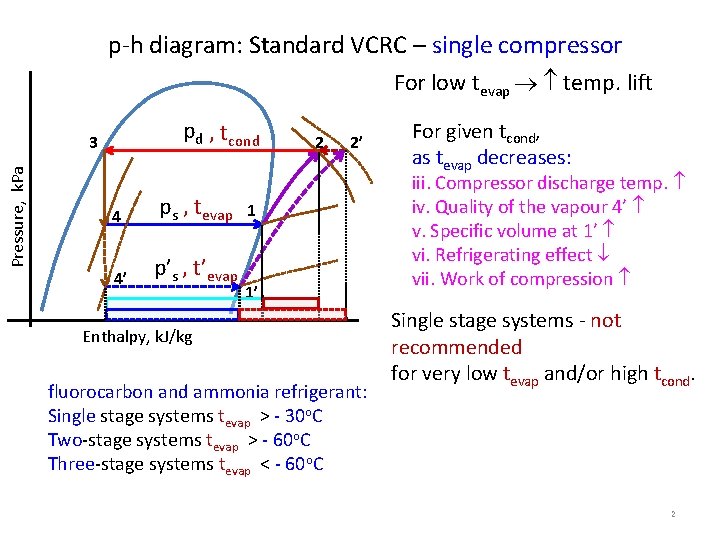
p-h diagram: Standard VCRC – single compressor For low tevap temp. lift pd , tcond Pressure, k. Pa 3 4 ps , tevap 4’ p’s , t’evap 2 2’ 1 1’ Enthalpy, k. J/kg fluorocarbon and ammonia refrigerant: Single stage systems tevap > - 30 o. C Two-stage systems tevap > - 60 o. C Three-stage systems tevap < - 60 o. C For given tcond, as tevap decreases: iii. Compressor discharge temp. iv. Quality of the vapour 4’ v. Specific volume at 1’ vi. Refrigerating effect vii. Work of compression Single stage systems - not recommended for very low tevap and/or high tcond. 2

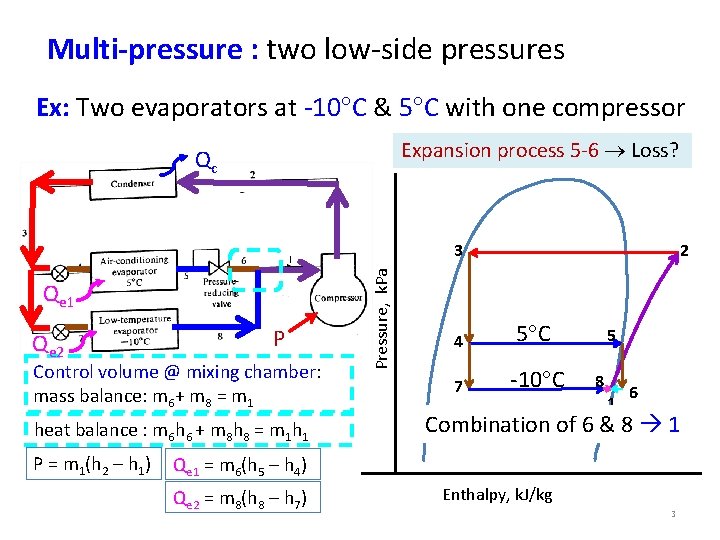
Multi-pressure : two low-side pressures Ex: Two evaporators at -10 C & 5 C with one compressor Expansion process 5 -6 Loss? Qc Qe 1 Qe 2 P Control volume @ mixing chamber: mass balance: m 6+ m 8 = m 1 heat balance : m 6 h 6 + m 8 h 8 = m 1 h 1 P = m 1(h 2 – h 1) Pressure, k. Pa 3 2 4 5 C 7 -10 C 5 8 1 6 Combination of 6 & 8 1 Qe 1 = m 6(h 5 – h 4) Qe 2 = m 8(h 8 – h 7) Enthalpy, k. J/kg 3

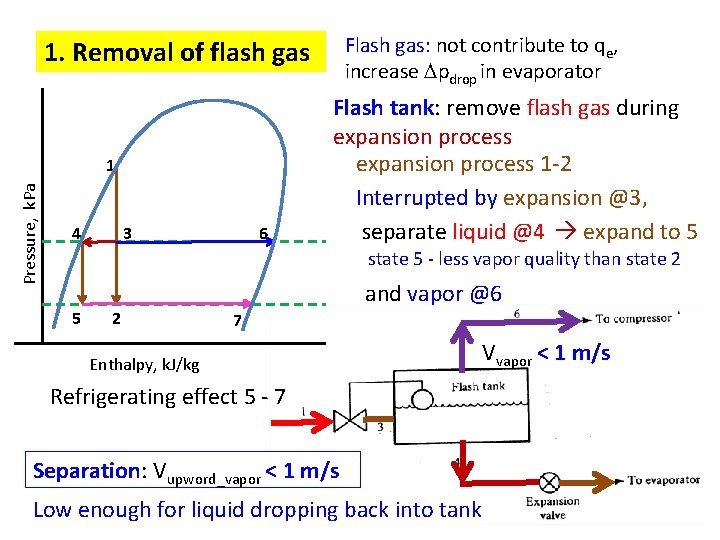
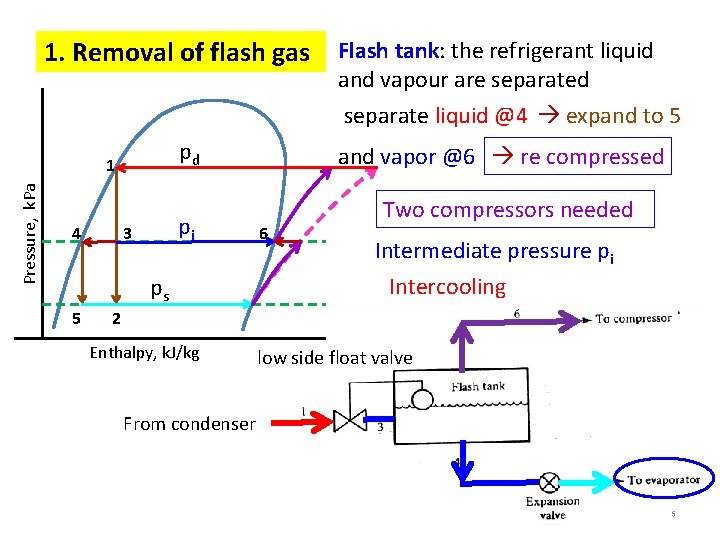
Flash gas: not contribute to qe, increase pdrop in evaporator 1. Removal of flash gas Pressure, k. Pa 1 4 3 6 Flash tank: remove flash gas during expansion process 1 -2 Interrupted by expansion @3, separate liquid @4 expand to 5 state 5 - less vapor quality than state 2 5 2 and vapor @6 7 Enthalpy, k. J/kg Vvapor < 1 m/s Refrigerating effect 5 - 7 Separation: Vupword_vapor < 1 m/s Low enough for liquid dropping back into tank 4

1. Removal of flash gas Flash tank: the refrigerant liquid and vapour are separated separate liquid @4 expand to 5 pd Pressure, k. Pa 1 4 pi 3 ps 5 and vapor @6 re compressed 6 Two compressors needed Intermediate pressure pi Intercooling 2 Enthalpy, k. J/kg low side float valve From condenser 5

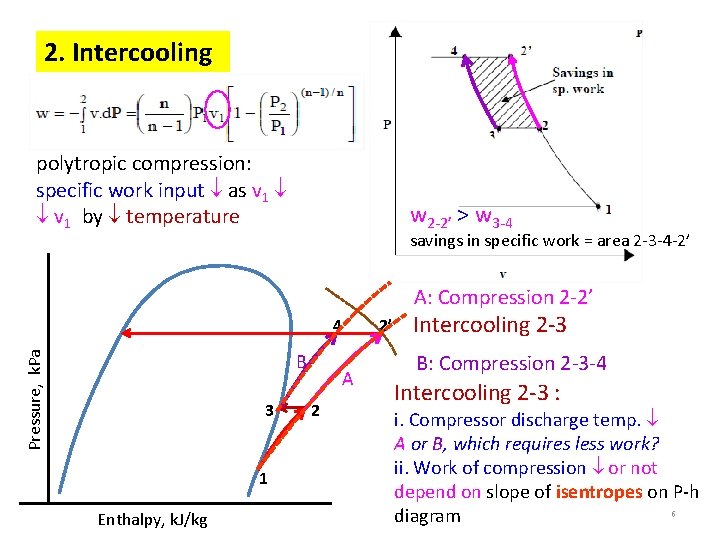
2. Intercooling polytropic compression: specific work input as v 1 by temperature w 2 -2’ > w 3 -4 savings in specific work = area 2 -3 -4 -2’ A: Compression 2 -2’ Pressure, k. Pa 4 B 3 1 Enthalpy, k. J/kg A 2 2’ Intercooling 2 -3 B: Compression 2 -3 -4 Intercooling 2 -3 : i. Compressor discharge temp. A or B, which requires less work? ii. Work of compression or not depend on slope of isentropes on P-h 6 diagram

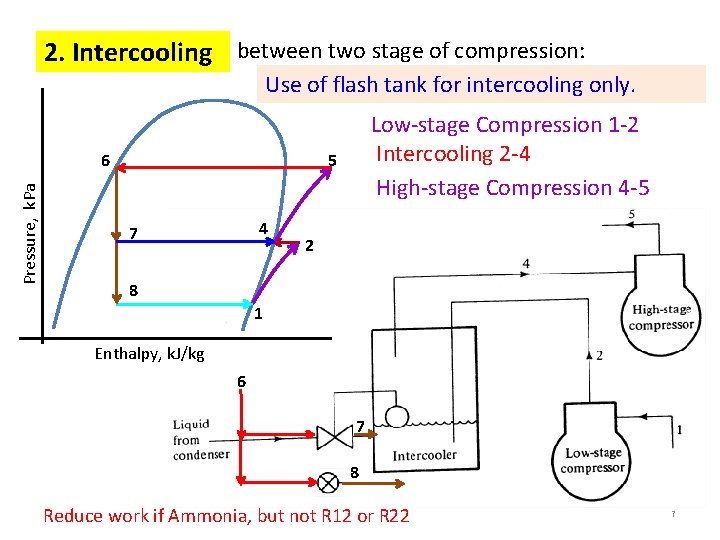
2. Intercooling between two stage of compression: Use of flash tank for intercooling only. Pressure, k. Pa 6 Low-stage Compression 1 -2 Intercooling 2 -4 High-stage Compression 4 -5 5 4 7 2 8 1 Enthalpy, k. J/kg 6 7 8 Reduce work if Ammonia, but not R 12 or R 22 7

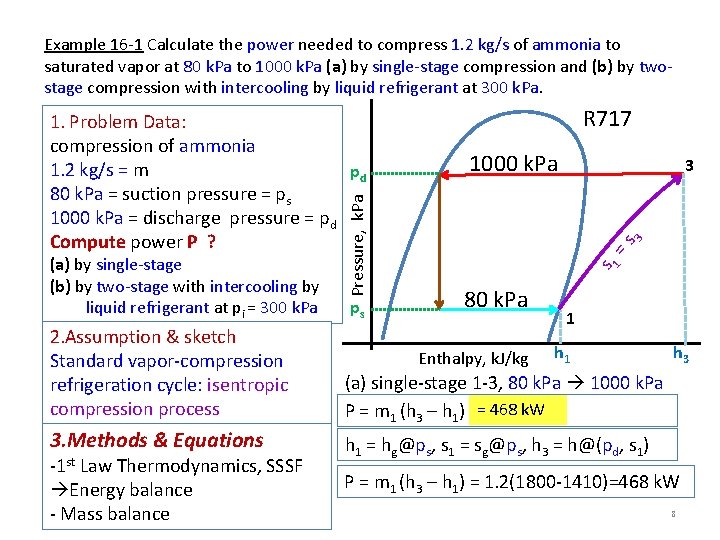
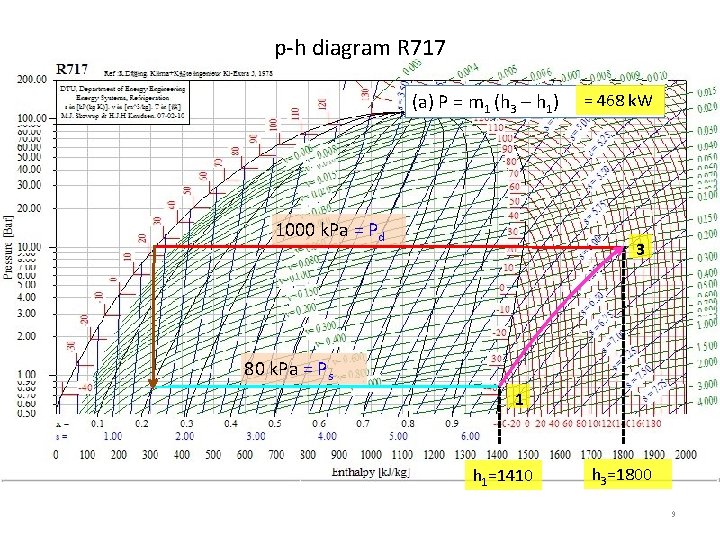
Example 16 -1 Calculate the power needed to compress 1. 2 kg/s of ammonia to saturated vapor at 80 k. Pa to 1000 k. Pa (a) by single-stage compression and (b) by twostage compression with intercooling by liquid refrigerant at 300 k. Pa. ps R 717 1000 k. Pa =s 3 3 s 1 (a) by single-stage (b) by two-stage with intercooling by liquid refrigerant at pi = 300 k. Pa Pressure, k. Pa 1. Problem Data: compression of ammonia 1. 2 kg/s = m pd 80 k. Pa = suction pressure = ps 1000 k. Pa = discharge pressure = pd Compute power P ? 80 k. Pa 1 2. Assumption & sketch Standard vapor-compression refrigeration cycle: isentropic compression process (a) single-stage 1 -3, 80 k. Pa 1000 k. Pa P = m 1 (h 3 – h 1) = 468 k. W 3. Methods & Equations h 1 = hg@ps, s 1 = sg@ps, h 3 = h@(pd, s 1) -1 st Law Thermodynamics, SSSF Energy balance - Mass balance Enthalpy, k. J/kg h 1 h 3 P = m 1 (h 3 – h 1) = 1. 2(1800 -1410)=468 k. W 8

p-h diagram R 717 (a) P = m 1 (h 3 – h 1) 1000 k. Pa = Pd = 468 k. W 3 80 k. Pa = Ps 1 h 1=1410 h 3=1800 9

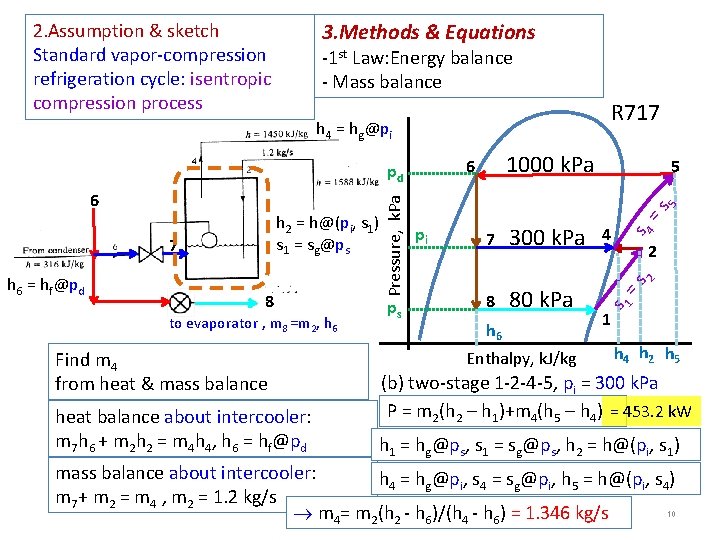
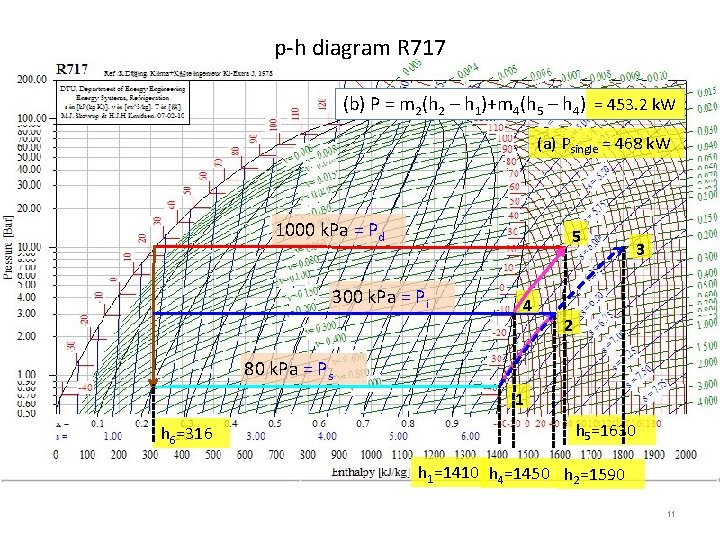
3. Methods & Equations 2. Assumption & sketch Standard vapor-compression refrigeration cycle: isentropic compression process -1 st Law: Energy balance - Mass balance R 717 h 4 = hg@pi 8 to evaporator , m 8 =m 2, h 6 Find m 4 from heat & mass balance heat balance about intercooler: m 7 h 6 + m 2 h 2 = m 4 h 4, h 6 = hf@pd ps 5 =s 300 k. Pa 4 8 80 k. Pa s 4 7 2 2 h 6 = hf@pd pi h 6 Enthalpy, k. J/kg =s 7 5 s 1 h 2 = h@(pi, s 1) s 1 = sg@ps Pressure, k. Pa 6 1000 k. Pa 6 pd 1 h 4 h 2 h 5 (b) two-stage 1 -2 -4 -5, pi = 300 k. Pa P = m 2(h 2 – h 1)+m 4(h 5 – h 4) = 453. 2 k. W h 1 = hg@ps, s 1 = sg@ps, h 2 = h@(pi, s 1) mass balance about intercooler: h 4 = hg@pi, s 4 = sg@pi, h 5 = h@(pi, s 4) m 7+ m 2 = m 4 , m 2 = 1. 2 kg/s 10 m 4= m 2(h 2 - h 6)/(h 4 - h 6) = 1. 346 kg/s

p-h diagram R 717 (b) P = m 2(h 2 – h 1)+m 4(h 5 – h 4) = 453. 2 k. W (a) Psingle = 468 k. W 1000 k. Pa = Pd 5 300 k. Pa = Pi 4 3 2 80 k. Pa = Ps 1 h 6=316 h 5=1630 h 1=1410 h 4=1450 h 2=1590 11

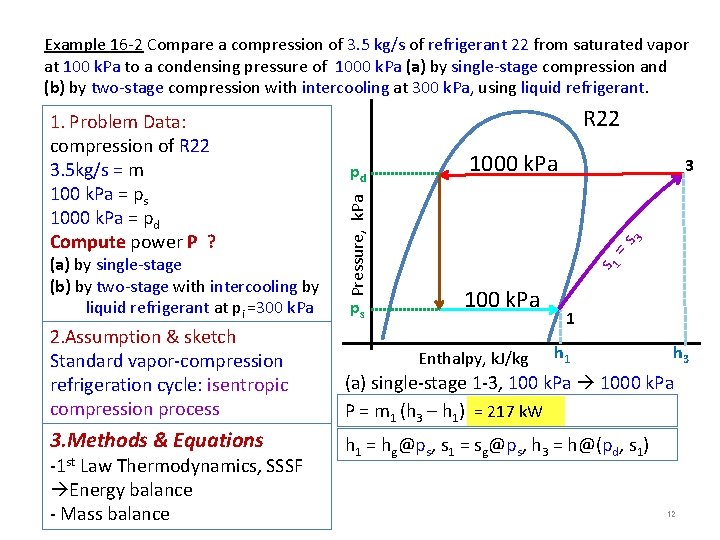
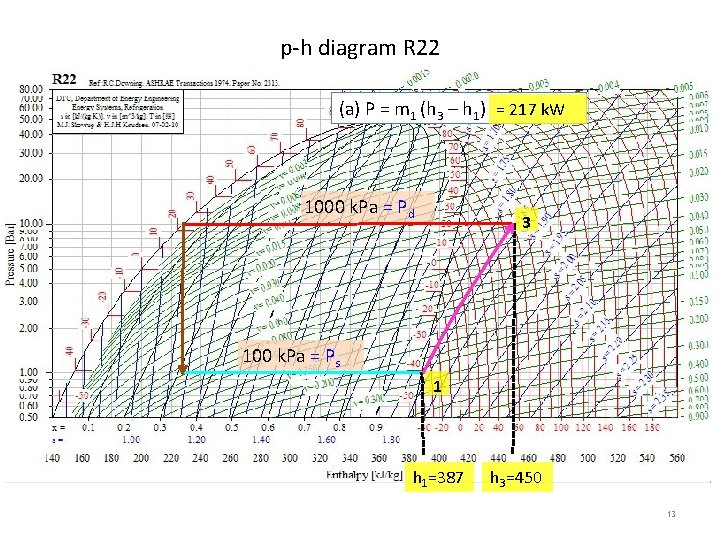
Example 16 -2 Compare a compression of 3. 5 kg/s of refrigerant 22 from saturated vapor at 100 k. Pa to a condensing pressure of 1000 k. Pa (a) by single-stage compression and (b) by two-stage compression with intercooling at 300 k. Pa, using liquid refrigerant. ps 1000 k. Pa 3 3 =s pd s 1 (a) by single-stage (b) by two-stage with intercooling by liquid refrigerant at pi =300 k. Pa R 22 Pressure, k. Pa 1. Problem Data: compression of R 22 3. 5 kg/s = m 100 k. Pa = ps 1000 k. Pa = pd Compute power P ? 100 k. Pa 1 2. Assumption & sketch Standard vapor-compression refrigeration cycle: isentropic compression process (a) single-stage 1 -3, 100 k. Pa 1000 k. Pa P = m 1 (h 3 – h 1) = 217 k. W 3. Methods & Equations h 1 = hg@ps, s 1 = sg@ps, h 3 = h@(pd, s 1) -1 st Law Thermodynamics, SSSF Energy balance - Mass balance Enthalpy, k. J/kg h 1 h 3 12

p-h diagram R 22 (a) P = m 1 (h 3 – h 1) = 217 k. W 1000 k. Pa = Pd 3 100 k. Pa = Ps 1 h 1=387 h 3=450 13

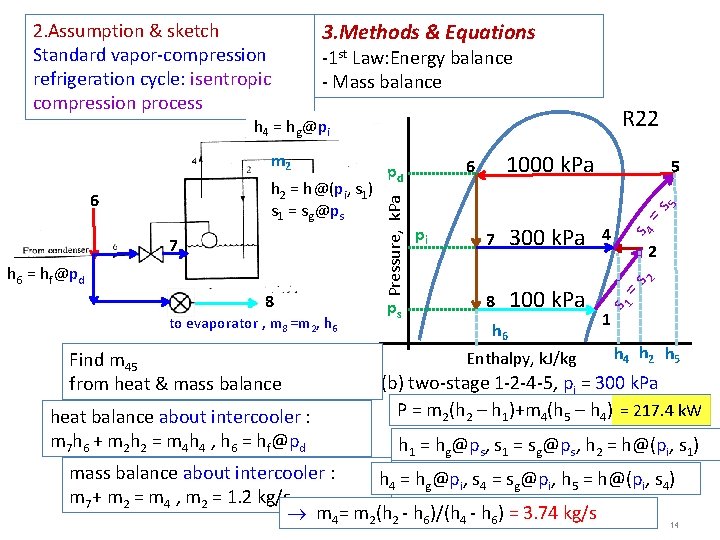
3. Methods & Equations -1 st Law: Energy balance - Mass balance R 22 h 4 = hg@pi 8 to evaporator , m 8 =m 2, h 6 Find m 45 from heat & mass balance heat balance about intercooler : m 7 h 6 + m 2 h 2 = m 4 h 4 , h 6 = hf@pd ps 5 =s 7 300 k. Pa 4 8 100 k. Pa 2 2 h 6 = hf@pd pi h 6 Enthalpy, k. J/kg =s 7 5 s 1 h 2 = h@(pi, s 1) s 1 = sg@ps 6 1000 k. Pa 6 pd Pressure, k. Pa m 2 s 4 2. Assumption & sketch Standard vapor-compression refrigeration cycle: isentropic compression process 1 h 4 h 2 h 5 (b) two-stage 1 -2 -4 -5, pi = 300 k. Pa P = m 2(h 2 – h 1)+m 4(h 5 – h 4) = 217. 4 k. W h 1 = hg@ps, s 1 = sg@ps, h 2 = h@(pi, s 1) mass balance about intercooler : h 4 = hg@pi, s 4 = sg@pi, h 5 = h@(pi, s 4) m 7+ m 2 = m 4 , m 2 = 1. 2 kg/s m 4= m 2(h 2 - h 6)/(h 4 - h 6) = 3. 74 kg/s 14

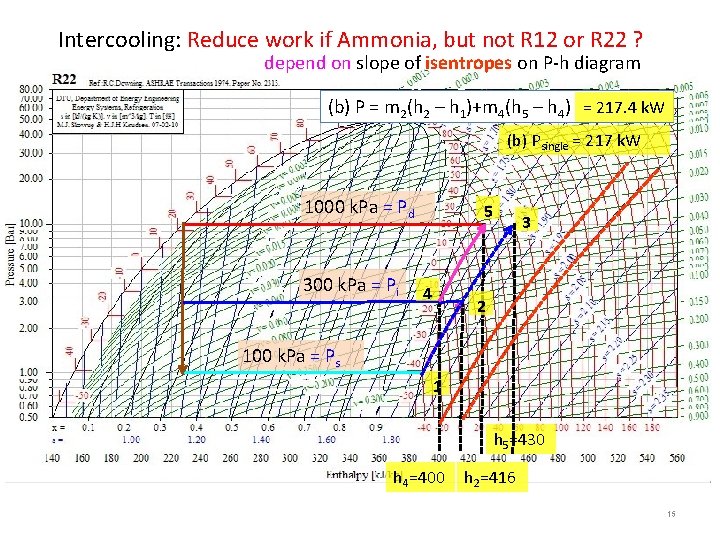
Intercooling: Reduce work if Ammonia, but not R 12 or R 22 ? depend on slope of isentropes on P-h diagram (b) P = m 2(h 2 – h 1)+m 4(h 5 – h 4) = 217. 4 k. W (b) Psingle = 217 k. W 1000 k. Pa = Pd 300 k. Pa = Pi 5 4 3 2 100 k. Pa = Ps 1 h 5=430 h 4=400 h 2=416 15

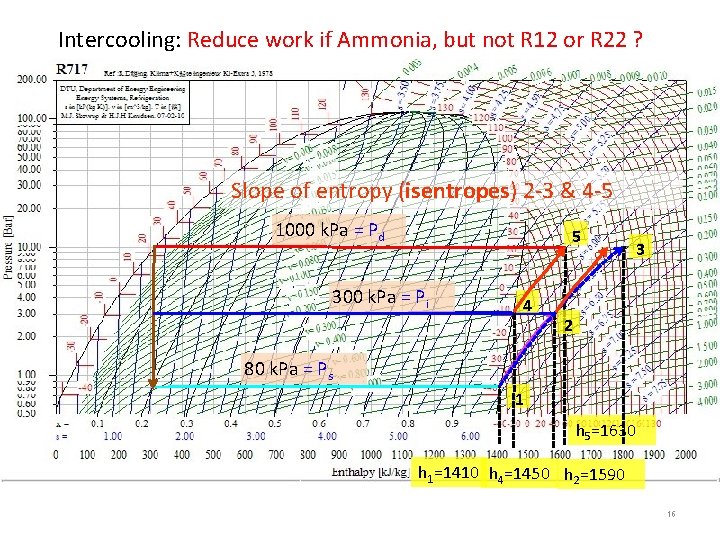
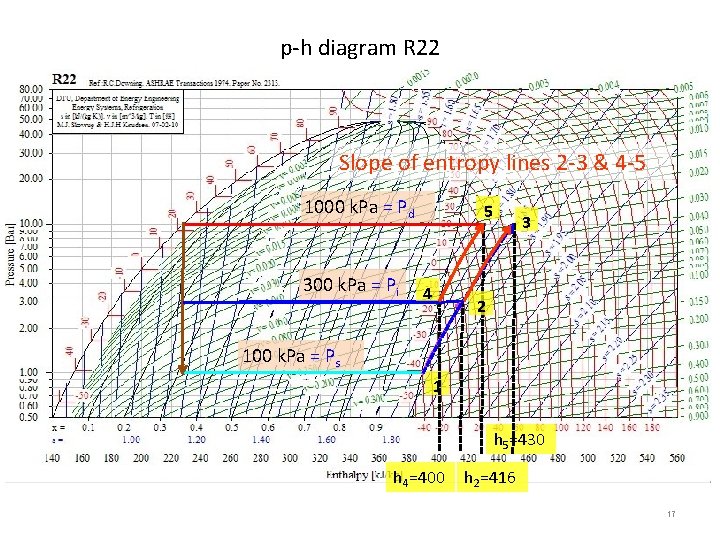
Intercooling: Reduce work if Ammonia, but not R 12 or R 22 ? Slope of entropy (isentropes) 2 -3 & 4 -5 1000 k. Pa = Pd 5 300 k. Pa = Pi 4 3 2 80 k. Pa = Ps 1 h 5=1630 h 1=1410 h 4=1450 h 2=1590 16

p-h diagram R 22 Slope of entropy lines 2 -3 & 4 -5 1000 k. Pa = Pd 300 k. Pa = Pi 5 4 3 2 100 k. Pa = Ps 1 h 5=430 h 4=400 h 2=416 17

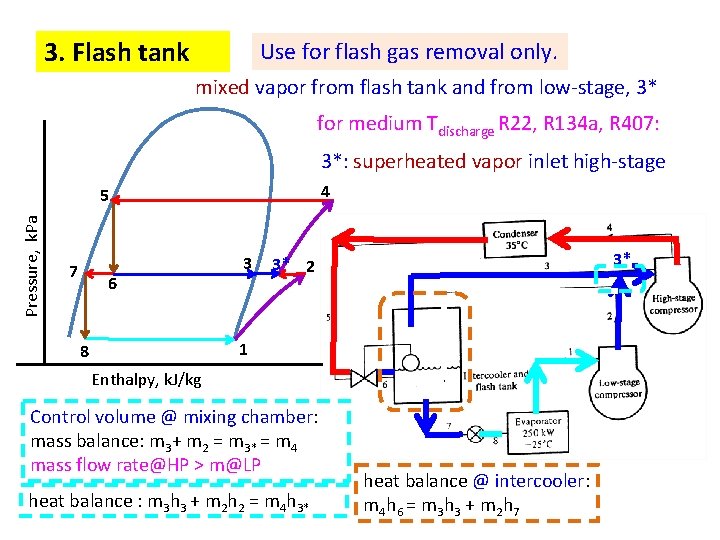
3. Flash tank Use for flash gas removal only. mixed vapor from flash tank and from low-stage, 3* for medium Tdischarge R 22, R 134 a, R 407: 3*: superheated vapor inlet high-stage 4 Pressure, k. Pa 5 7 6 3 3* 3* 2 1 8 Enthalpy, k. J/kg Control volume @ mixing chamber: mass balance: m 3+ m 2 = m 3* = m 4 mass flow rate@HP > m@LP heat balance : m 3 h 3 + m 2 h 2 = m 4 h 3* heat balance @ intercooler: m 4 h 6 = m 3 h 3 + m 2 h 7

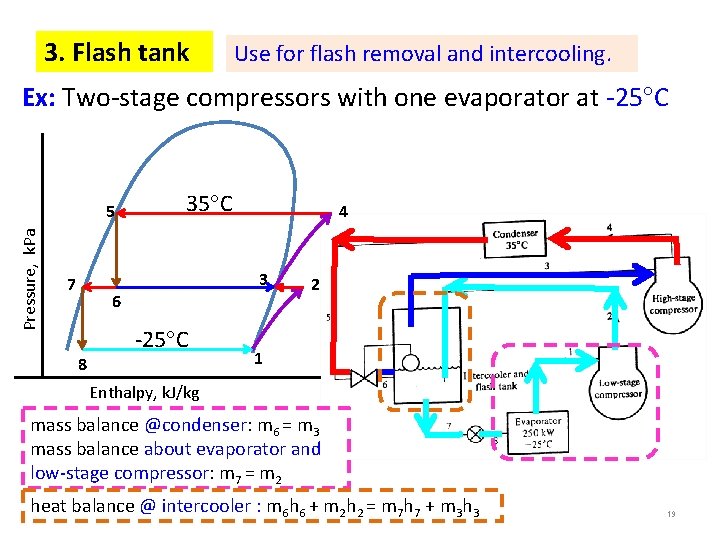
3. Flash tank Use for flash removal and intercooling. Ex: Two-stage compressors with one evaporator at -25 C Pressure, k. Pa 5 35 C 4 3 7 6 8 -25 C 2 1 Enthalpy, k. J/kg mass balance @condenser: m 6 = m 3 mass balance about evaporator and 19 low-stage compressor: m 7 = m 2 heat balance @ intercooler : m 6 h 6 + m 2 h 2 = m 7 h 7 + m 3 h 3 19

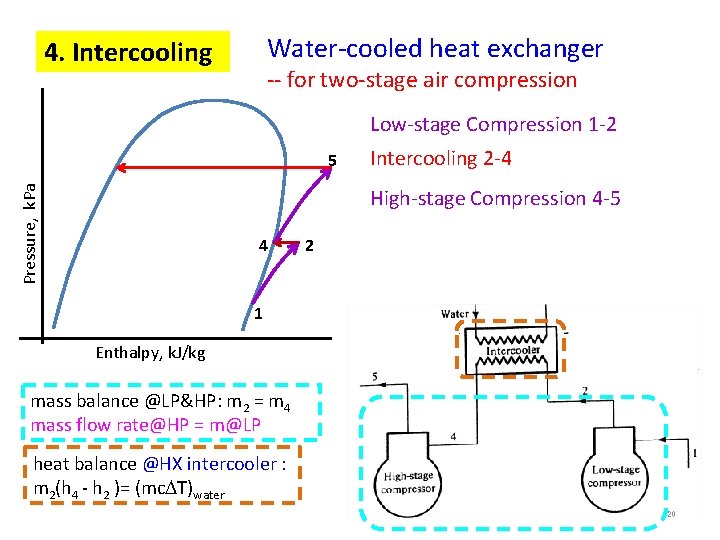
Water-cooled heat exchanger 4. Intercooling -- for two-stage air compression Low-stage Compression 1 -2 Pressure, k. Pa 5 Intercooling 2 -4 High-stage Compression 4 -5 4 2 1 Enthalpy, k. J/kg mass balance @LP&HP: m 2 = m 4 mass flow rate@HP = m@LP heat balance @HX intercooler : m 2(h 4 - h 2 )= (mc T)water 20

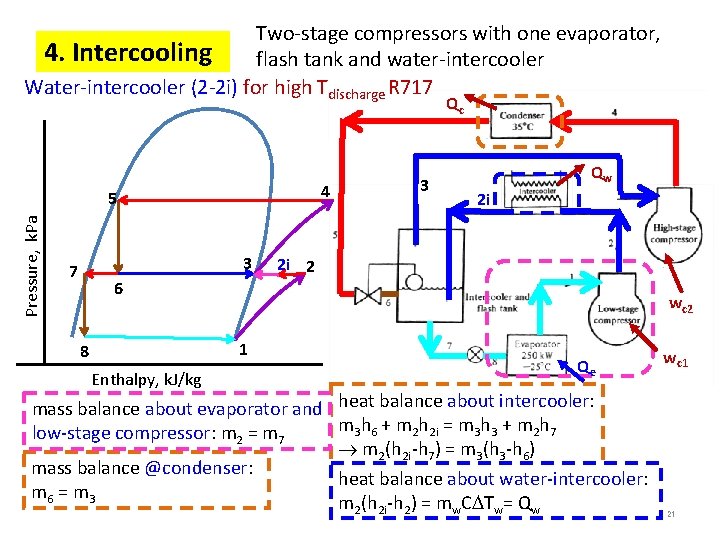
Two-stage compressors with one evaporator, 4. Intercooling flash tank and water-intercooler Water-intercooler (2 -2 i) for high Tdischarge R 717 Qc 4 Pressure, k. Pa 5 3 7 3 Qw 2 i 2 i 2 6 wc 2 c 1 8 Enthalpy, k. J/kg Qe mass balance about evaporator and heat balance about intercooler: m 3 h 6 + m 2 h 2 i = m 3 h 3 + m 2 h 7 low-stage compressor: m 2 = m 7 21 m 2(h 2 i-h 7) = m 3(h 3 -h 6) mass balance @condenser: heat balance about water-intercooler: m 6 = m 3 m 2(h 2 i-h 2) = mw. C Tw= Qw wc 1 21

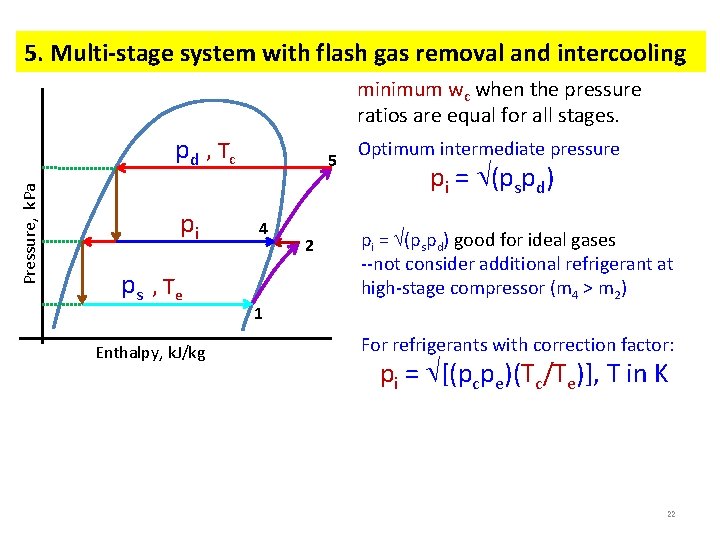
5. Multi-stage system with flash gas removal and intercooling minimum wc when the pressure ratios are equal for all stages. Pressure, k. Pa p d , Tc pi p s , Te Enthalpy, k. J/kg 5 4 1 2 Optimum intermediate pressure pi = (pspd) good for ideal gases --not consider additional refrigerant at high-stage compressor (m 4 > m 2) For refrigerants with correction factor: pi = [(pcpe)(Tc/Te)], T in K 22

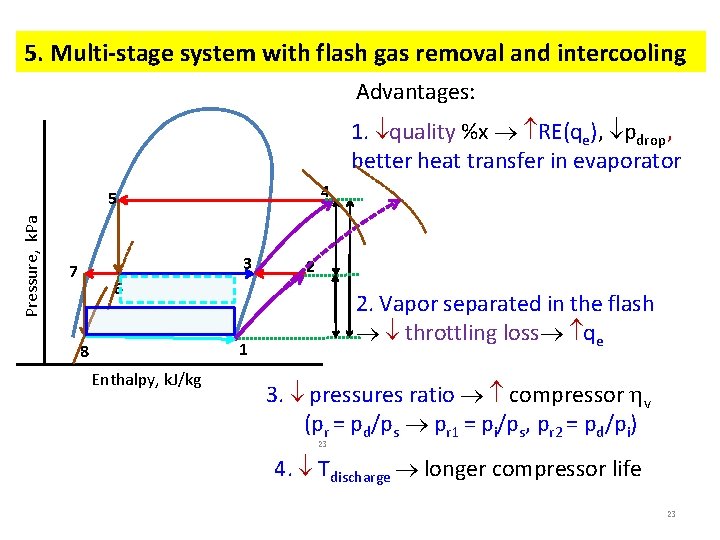
5. Multi-stage system with flash gas removal and intercooling Advantages: 1. quality %x RE(qe), pdrop, better heat transfer in evaporator 4 Pressure, k. Pa 5 3 7 2 6 2. Vapor separated in the flash throttling loss qe 1 8 Enthalpy, k. J/kg 3. pressures ratio compressor v (pr = pd/ps pr 1 = pi/ps, pr 2 = pd/pi) 23 4. Tdischarge longer compressor life 23

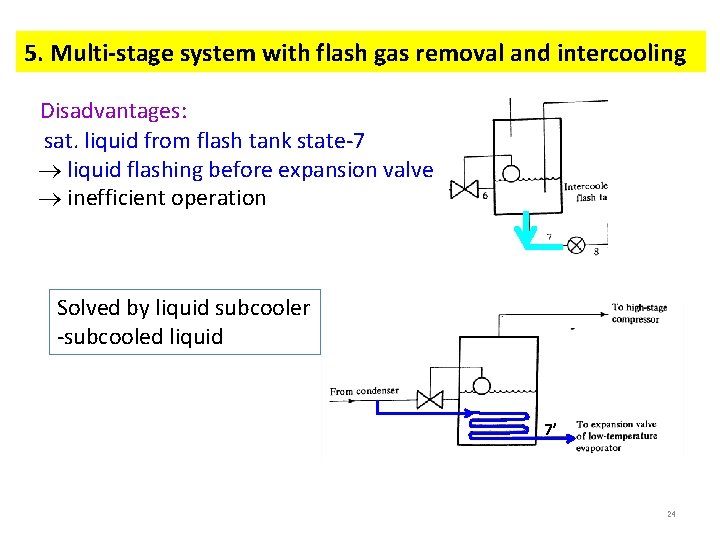
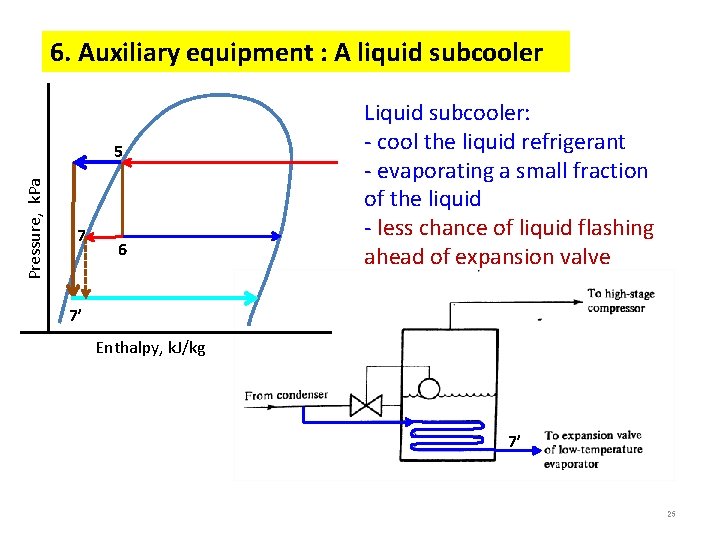
5. Multi-stage system with flash gas removal and intercooling Disadvantages: sat. liquid from flash tank state-7 liquid flashing before expansion valve inefficient operation Solved by liquid subcooler -subcooled liquid 7’ 24

6. Auxiliary equipment : A liquid subcooler Pressure, k. Pa 5 7 6 Liquid subcooler: - cool the liquid refrigerant - evaporating a small fraction of the liquid - less chance of liquid flashing ahead of expansion valve 7’ Enthalpy, k. J/kg 7’ 25

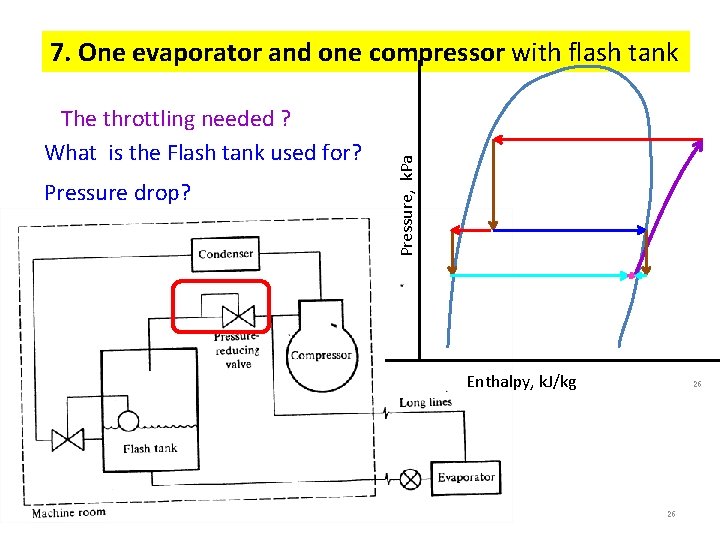
The throttling needed ? What is the Flash tank used for? Pressure drop? Pressure, k. Pa 7. One evaporator and one compressor with flash tank Enthalpy, k. J/kg 26 26

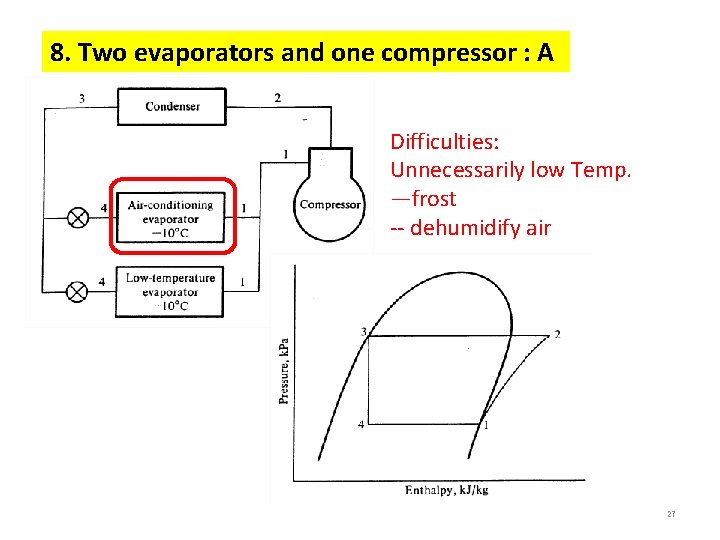
8. Two evaporators and one compressor : A Difficulties: Unnecessarily low Temp. —frost -- dehumidify air 27

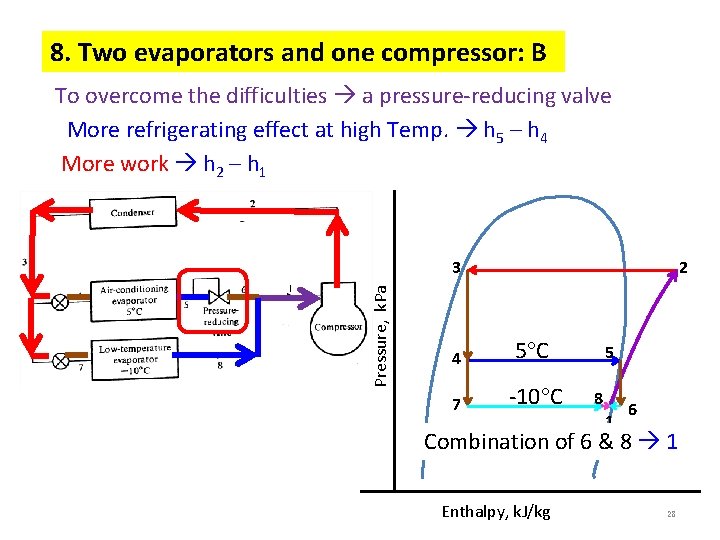
8. Two evaporators and one compressor: B To overcome the difficulties a pressure-reducing valve More refrigerating effect at high Temp. h 5 – h 4 More work h 2 – h 1 Pressure, k. Pa 3 2 4 5 C 7 -10 C 5 8 1 6 Combination of 6 & 8 1 Enthalpy, k. J/kg 28

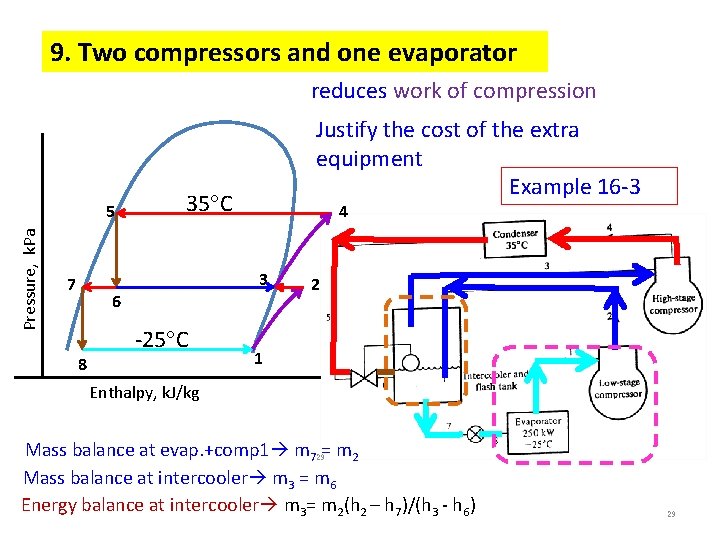
9. Two compressors and one evaporator reduces work of compression Pressure, k. Pa 5 Justify the cost of the extra equipment Example 16 -3 35 C 4 3 7 6 8 -25 C 2 1 Enthalpy, k. J/kg Mass balance at evap. +comp 1 m 729= m 2 Mass balance at intercooler m 3 = m 6 Energy balance at intercooler m 3= m 2(h 2 – h 7)/(h 3 - h 6) 29

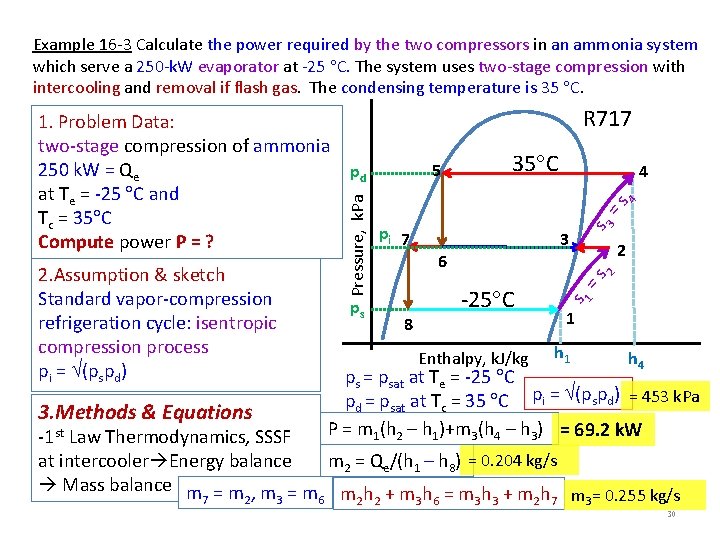
Example 16 -3 Calculate the power required by the two compressors in an ammonia system which serve a 250 -k. W evaporator at -25 C. The system uses two-stage compression with intercooling and removal if flash gas. The condensing temperature is 35 C. 3. Methods & Equations 5 ps 35 C 4 pi 7 s 3 =s 4 pd 3 2 8 -25 C Enthalpy, k. J/kg =s 2 6 s 1 2. Assumption & sketch Standard vapor-compression refrigeration cycle: isentropic compression process pi = (pspd) R 717 Pressure, k. Pa 1. Problem Data: two-stage compression of ammonia 250 k. W = Qe at Te = -25 C and Tc = 35 C Compute power P = ? 1 h 4 ps = psat at Te = -25 C pd = psat at Tc = 35 C pi = (pspd) = 453 k. Pa P = m 1(h 2 – h 1)+m 3(h 4 – h 3) = 69. 2 k. W -1 st Law Thermodynamics, SSSF m 2 = Qe/(h 1 – h 8) = 0. 204 kg/s at intercooler Energy balance Mass balance m = m , m = m m h + m h = m h + m h m = 0. 255 kg/s 7 2 3 6 2 2 3 6 3 3 2 7 3 30

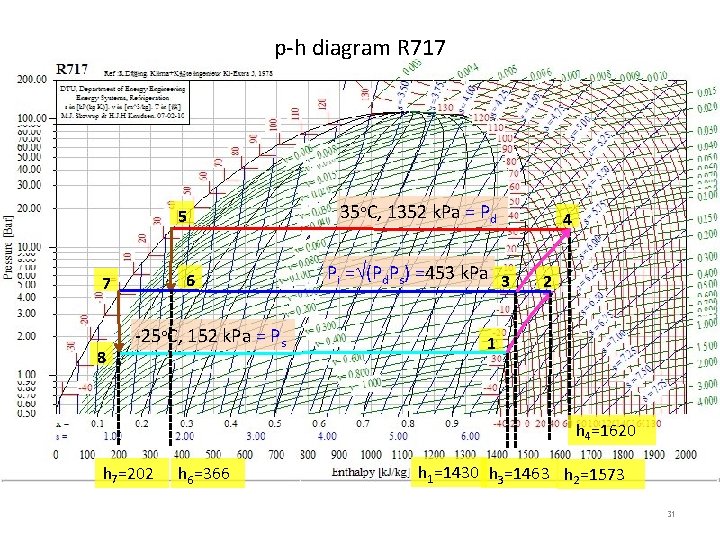
p-h diagram R 717 5 6 7 8 -25 C, 152 k. Pa = Ps 35 C, 1352 k. Pa = Pd Pi = (Pd. Ps) =453 k. Pa 3 4 2 1 h 4=1620 h 7=202 h 6=366 h 1=1430 h 3=1463 h 2=1573 31

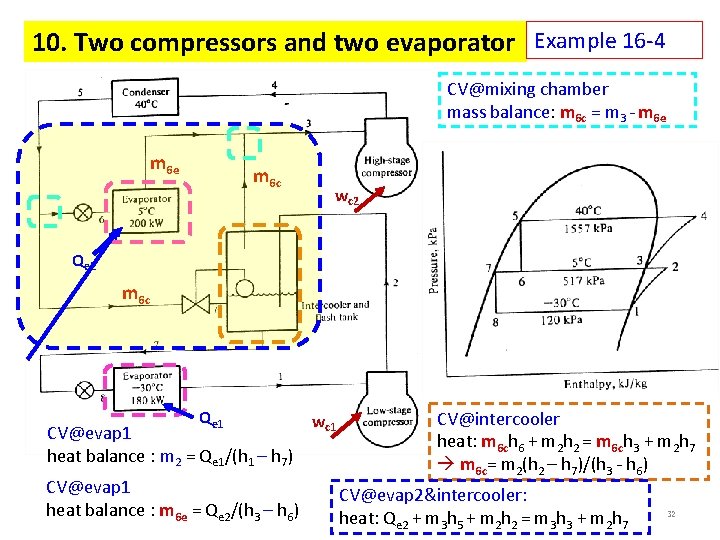
10. Two compressors and two evaporator Example 16 -4 CV@mixing chamber mass balance: m 6 c = m 3 - m 6 e m 6 c wc 2 Qe 2 m 6 c Qe 1 CV@evap 1 heat balance : m 2 = Qe 1/(h 1 – h 7) CV@evap 1 heat balance : m 6 e = Qe 2/(h 3 – h 6) wc 1 CV@intercooler heat: m 6 ch 6 + m 2 h 2 = m 6 ch 3 + m 2 h 7 m 6 c= m 2(h 2 – h 7)/(h 3 - h 6) CV@evap 2&intercooler: heat: Qe 2 + m 3 h 5 + m 2 h 2 = m 3 h 3 + m 2 h 7 32

Example 16 -4 In an ammonia system one evaporator is to provide 180 k. W of refrigeration at -30 C and another evaporator is to provide 200 k. W at 5 C. The system uses two-stage compression with intercoolomg and is arranged as in Fig. 16 -12 a. The condensing temperature is 40 C. Calculate the power required by the compressors. 1. Problem Data: two-stage compression of ammonia 180 k. W = Qe 1 at Te 1 = -30 C and 200 k. W = Qe 2 at Te 2 = 5 C Tc = 40 C Compute power P = ? 2. Assumption & sketch Standard vapor-compression refrigeration cycle: isentropic compression process 3. Methods & Equations Qe 2 Qe 1 P = m 1(h 2 – h 1)+m 3(h 4 – h 3) = 91. 5 k. W CV@evap 2: m 6 e = Qe 2/(h 3 – h 6) = 0. 185 kg/s -1 st Law Thermodynamics, SSSF CV@evap 1: m 2 = Qe 1/(h 1 – h 7) = 0. 150 kg/s Energy balance Mass balance CV@mixing chamber: m 7 = m 2, m 3 = m 6 e+m 6 c CV@intercooler heat: m 6 c= m 2(h 2 – h 7)/(h 3 - h 6) m 3 = 0. 382 kg/s or CV@evap 2&intercooler: Qe 2 + m 3 h 5 + m 2 h 2 = m 3 h 3 + m 2 h 7

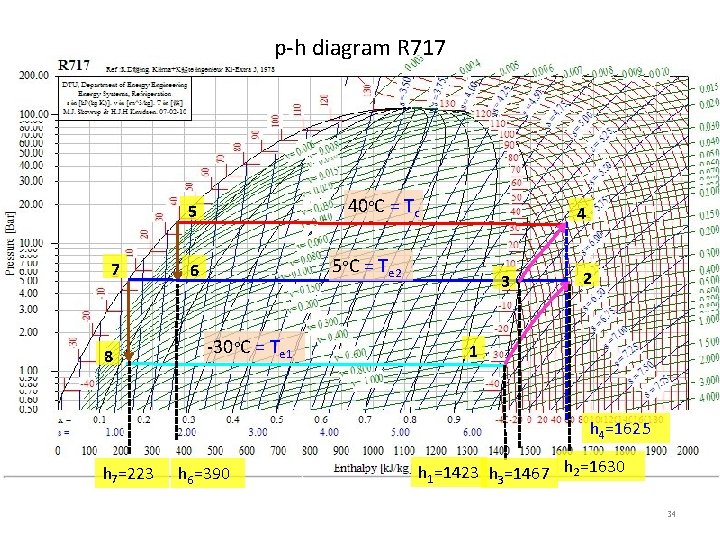
p-h diagram R 717 40 C = Tc 5 7 8 4 5 C = Te 2 6 -30 C = Te 1 3 2 1 h 4=1625 h 7=223 h 6=390 h 1=1423 h 3=1467 h 2=1630 34

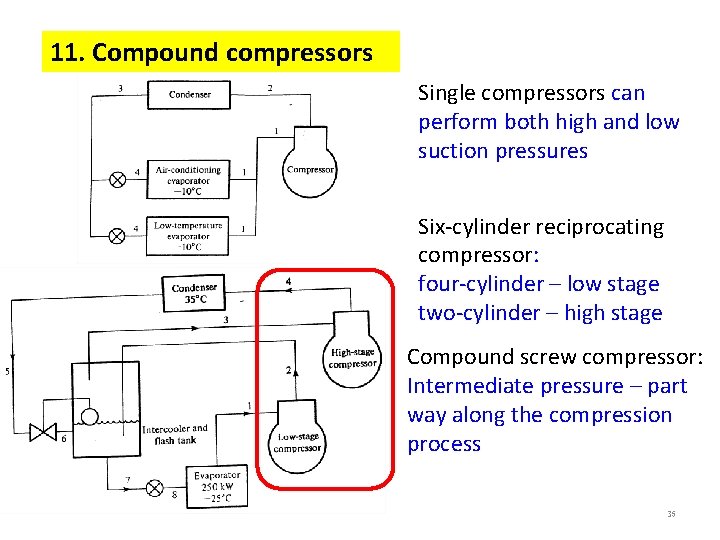
11. Compound compressors Single compressors can perform both high and low suction pressures Six-cylinder reciprocating compressor: four-cylinder – low stage two-cylinder – high stage Compound screw compressor: Intermediate pressure – part way along the compression process 35

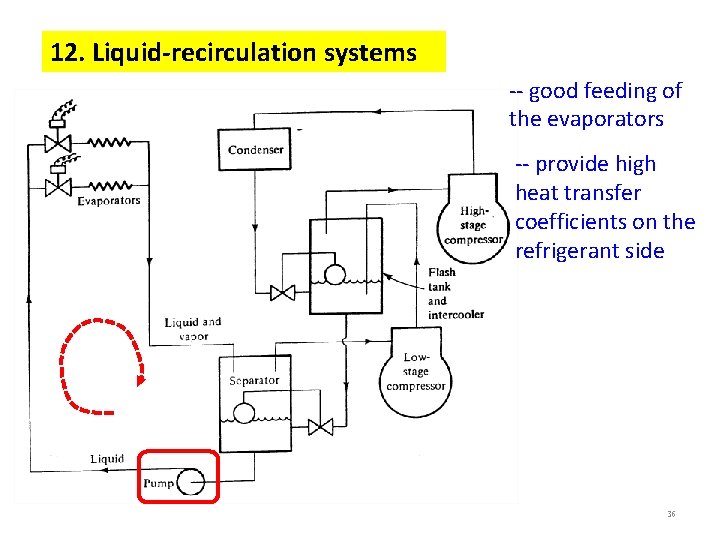
12. Liquid-recirculation systems -- good feeding of the evaporators -- provide high heat transfer coefficients on the refrigerant side 36

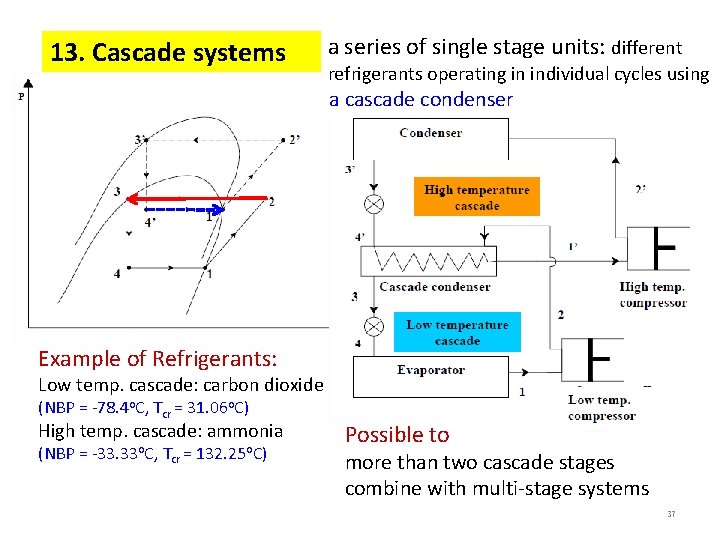
13. Cascade systems a series of single stage units: different refrigerants operating in individual cycles using a cascade condenser Example of Refrigerants: Low temp. cascade: carbon dioxide (NBP = -78. 4 o. C, Tcr = 31. 06 o. C) High temp. cascade: ammonia (NBP = -33. 33 o. C, Tcr = 132. 25 o. C) Possible to more than two cascade stages combine with multi-stage systems 37

14. Summary Flash tank: remove flash gas during expansion process - decrease the power required by the compressors Intercooling between two stage of compression: - reduces work of compression for ammonia -reduces the discharge temp. reduce : oil carbonization : sticky compressor valves : lubrication difficulties in reciprocating compressor Decision based on economic: saving & additional cost Factors: refrigerant, type of compressor, size of system Screw compressors – handle larger pressure ratio than reciprocating compressors Multistage compression: decrease pressure ratio reduce wear on bearing surfaces 38