TOPIC 1 Describing Motion AVERAGE SPEED One way

TOPIC 1: Describing Motion

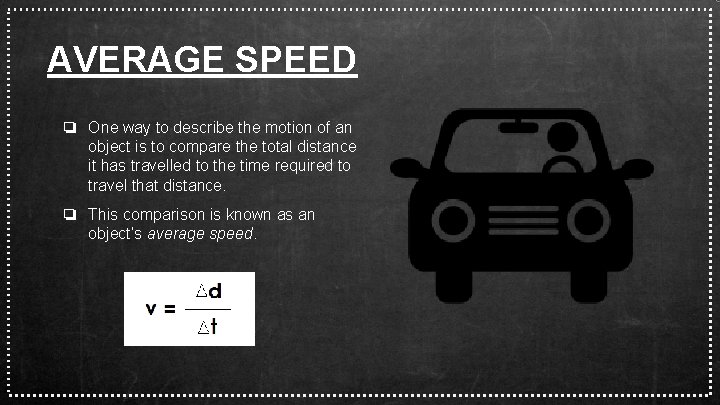
AVERAGE SPEED ❏ One way to describe the motion of an object is to compare the total distance it has travelled to the time required to travel that distance. ❏ This comparison is known as an object’s average speed.

Calculating Average Speed: Examples ❏ A cyclist travels a distance of 40. 0 km over a period of 2. 5 h. What is the cyclist’s average speed? ❏ A cheetah runs at an average speed of 80 km/h. If the cheetah runs for a period of 0. 15 h, how far does it travel? ❏ A taxi drives a distance of 298 km from Calgary to Edmonton. If the taxi travels at an average speed of 110 km/h, how long will it take to reach its destination?

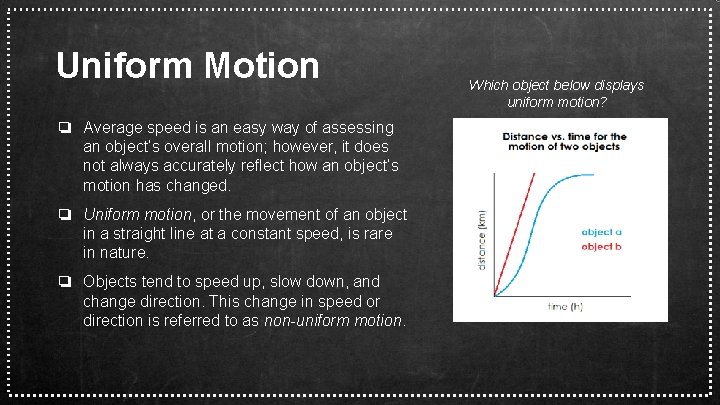
Uniform Motion ❏ Average speed is an easy way of assessing an object’s overall motion; however, it does not always accurately reflect how an object’s motion has changed. ❏ Uniform motion, or the movement of an object in a straight line at a constant speed, is rare in nature. ❏ Objects tend to speed up, slow down, and change direction. This change in speed or direction is referred to as non-uniform motion. Which object below displays uniform motion?

Speed Limits? ❏ Vehicles do not typically travel with uniform motion (except for on long, straight highways). What, then, are speed limits referring to? ❏ Rather than referring to average speed, speed limits actually indicate the speed that you should be travelling at that instant in time. ❏ This is known as instantaneous speed.

Scalar Quantities ❏ Average speed is an example of of a scalar quantity. ❏ Scalar quantities are measurements that do not include direction. ❏ Time and volume are other examples of scalar quantities.

Unit Conversions ❏ Although highway speed limits are understood to be a measurement of km/h in Canada, average speed can also be measured in m/s ❏ To convert from m/s to km/h (or vice versa), it is important to recall that 1 km contains 1000 meters, and 1 hour contains 3600 seconds.

Unit Conversions: Example ❏ An owl is able to drop a distance of 1. 30 m in 0. 80 s to capture its prey. Determine the owl’s average speed during its descent in km/h. METHOD 1: Convert meters to km and seconds to hours before calculating your answer METHOD 2: Calculate the answer in m/s and then use unit analysis to convert your answer into km/h

AVERAGE VELOCITY ❏ If you want to know how fast an object is moving, the average speed of the object is useful; however, average speed does not reveal anything about the direction of motion. ❏ Average velocity describes both how fast an object is moving and the direction it moves.

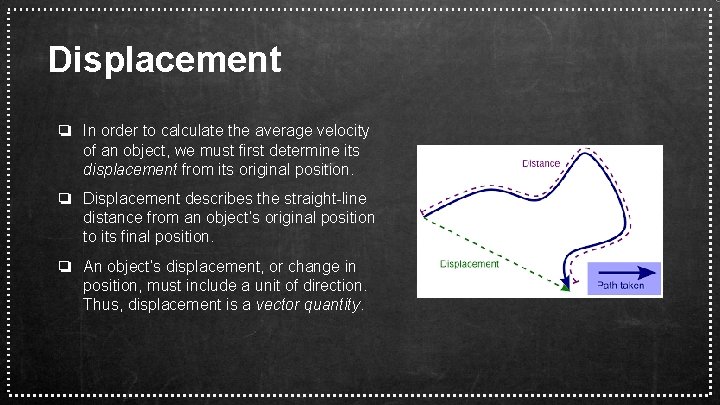
Displacement ❏ In order to calculate the average velocity of an object, we must first determine its displacement from its original position. ❏ Displacement describes the straight-line distance from an object’s original position to its final position. ❏ An object’s displacement, or change in position, must include a unit of direction. Thus, displacement is a vector quantity.

Calculating Displacement ❏ When displacement is calculated, it is convenient to assign a sign (+ or -) to each direction. ❏ Conventionally, North = + and South = ❏ For example, if a vehicle travels 50 km [S] and then turns around and travels another 75 km [N], its total displacement may be calculated by adding these two distances together with their appropriate signs: Displacement = (-50 km) + (+75 km) = +25 km or 25 km [N]

Calculating Displacement ❏ We can also use a diagram to help calculate displacement. ❏ Consider the previous example: If a vehicle travels 50 km [S] and then turns around and travels another 75 km [N], what is its total displacement? Displacement = (-50 km) + (+75 km) = +25 km or 25 km [N]

Calculating Displacement: Examples ❏ If John walks 2. 6 km [N] to school in the morning and returns home along the same path in the afternoon, what is John’s total displacement from his house at the end of the day? ❏ If John walks 2. 6 km [N] to school in the morning and another 0. 2 km [N] to his friends house after school, what is John’s total displacement from his home at the end of the day? ❏ John walks 2. 6 km [N] to school in the morning. After school, he walks 3. 8 km [S] to work. What is John’s total displacement from his home at the end of the day?

Calculating Average Velocity: Examples Now that you know how to calculate displacement, you should be able to determine the velocity of an object. Recall that velocity can be calculated by dividing an object’s displacement by the amount of time required to travel that distance. ❏ A vehicle travels 110 km [N] and then turns around and travels another 24 km [S]. If the entire trip takes 1. 2 h to complete, what must have been the average velocity of the vehicle? ❏ A soccer player kicks the ball forward 9. 5 m to their teammate, who then directs the ball another 5. 3 m forward into the net. If the ball reaches the net in 4. 3 s after being kicked by the first player, what is the average velocity of the ball?

Calculating Average Velocity: Examples ❏ An antelope travels 13. 5 km [N] from its home. If it requires 0. 30 h to travel this distance, what is the antelope’s velocity? ❏ A cyclist travels at a velocity of 23 km/h [W]. What will be their total displacement after a period of 0. 25 h? ❏ An object’s displacement from its original position is +0. 55 m. If it travels that distance at a velocity of 1. 3 m/s, how long did it require to reach its destination?

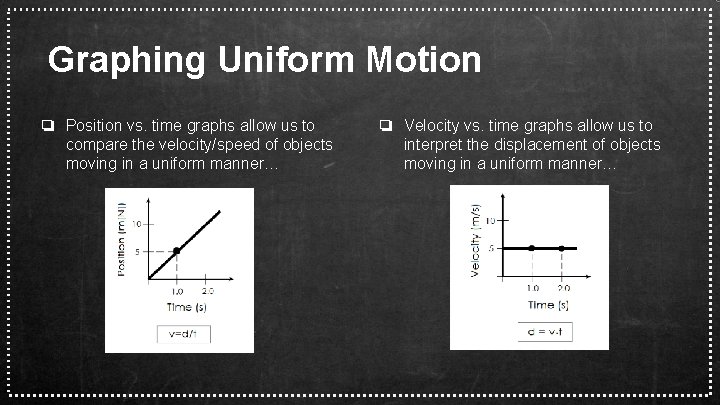
Graphing Uniform Motion ❏ Position vs. time graphs allow us to compare the velocity/speed of objects moving in a uniform manner… ❏ Velocity vs. time graphs allow us to interpret the displacement of objects moving in a uniform manner…

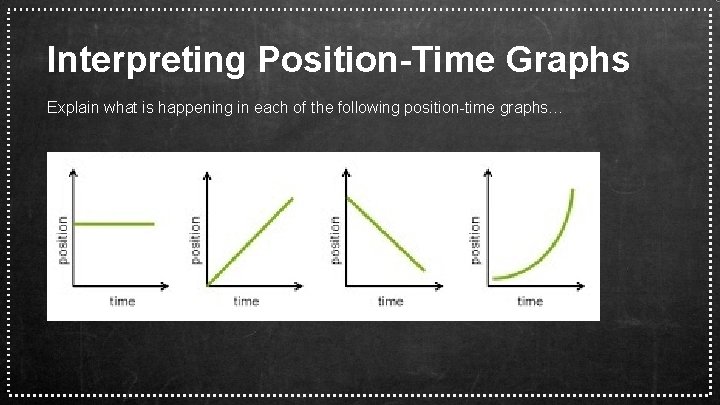
Interpreting Position-Time Graphs Explain what is happening in each of the following position-time graphs…

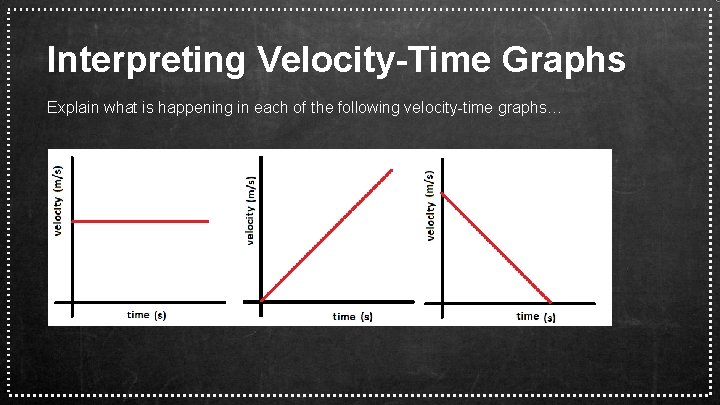
Interpreting Velocity-Time Graphs Explain what is happening in each of the following velocity-time graphs…

ACCELERATION ❏ If an object is speeding up or slowing down, it is no longer moving with uniform motion; instead, it is said to be moving with non-uniform motion. ❏ Acceleration is a type of nonuniform motion that describes the change in velocity that occurs over a specific time interval. ❏ Acceleration is typically measured in units of m/s 2

Calculating Acceleration: Examples ❏ A car travelling 70 km/h east speeds up over a period of 4. 5 s to travel at a velocity of 90 km/h east. Determine the average acceleration of the car in m/s 2 ❏ A sprinter on a high school track team can achieve an average acceleration of 3. 0 m/s 2 from rest to a maximum velocity of 11. 0 m/s. How long does it take the sprinter to reach this maximum velocity? ❏ A group of children riding an inflatable tube start from rest and travel down a hill, accelerating at an average rate of 1. 15 m/s 2. Determine the speed the tube reaches near the bottom of the hill after travelling for 6. 0 s.

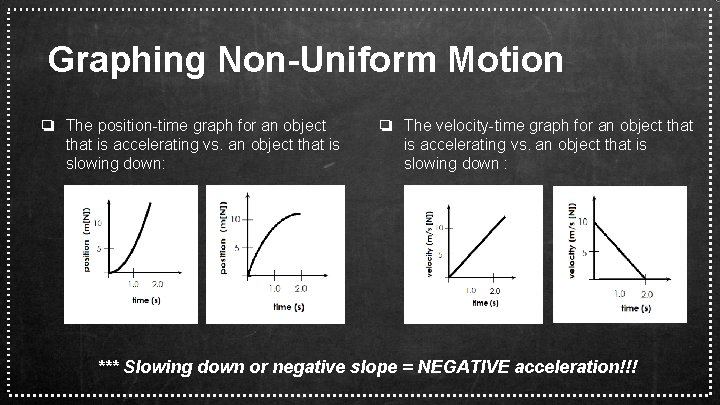
Graphing Non-Uniform Motion ❏ The position-time graph for an object that is accelerating vs. an object that is slowing down: ❏ The velocity-time graph for an object that is accelerating vs. an object that is slowing down : *** Slowing down or negative slope = NEGATIVE acceleration!!!

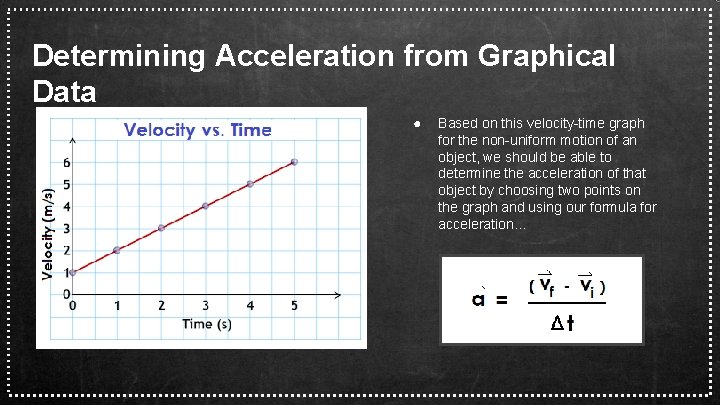
Determining Acceleration from Graphical Data ● Based on this velocity-time graph for the non-uniform motion of an object, we should be able to determine the acceleration of that object by choosing two points on the graph and using our formula for acceleration…

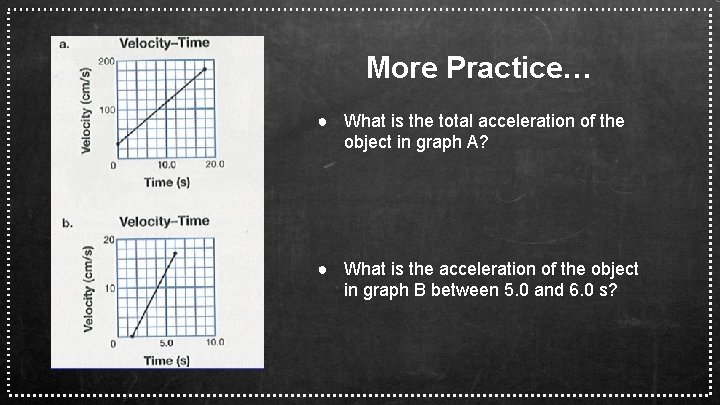
More Practice… ● What is the total acceleration of the object in graph A? ● What is the acceleration of the object in graph B between 5. 0 and 6. 0 s?

Calculating Displacement during Accelerated Motion ❏ The displacement of an object during acceleration may be calculated by multiplying the average velocity of an object by the time interval in which it travelled at said velocity… EXAMPLE: A car merges into a highway with an initial velocity of 65. 0 km/h [E]. The car reaches a final velocity of 100. 0 km/h [E] in 4. 00 s. Calculate the displacement of the car in meters.

Acceleration due to Gravity ❏ All objects, regardless of their mass, fall to the earth’s surface with an average acceleration of 9. 81 m/s 2. This value is referred to as the acceleration due to gravity. ❏ Note that acceleration due to gravity does not take into account air resistance. ❏ If applied to the equation for acceleration, this allows us to solve for the final or initial velocity of an object that is falling as well as the time required to fall.

Acceleration due to Gravity: Example ❏ During a baseball game, a ball leaves a bat and travels straight up into the air. At its highest point, the ball travels a displacement of 18. 5 m from the bat. Determine the amount of time the ball will take to fall back down to the batter from its highest point if its final velocity before reaching the batter is 11. 5 m/s. (remember: acceleration due to gravity = 9. 81 m/s 2 !)

Another way of Calculating Displacement during Accelerated Motion ❏ What if the final velocity of an object is not given, but its acceleration IS provided? ? ? ❏ Our original formula no longer allows us to find displacement. Instead, we must use this formula: EXAMPLE: John leaves the surface of a trampoline with an initial velocity of 11. 8 m/s and travels straight up. Determine the displacement of the gymnast after 0. 80 s.

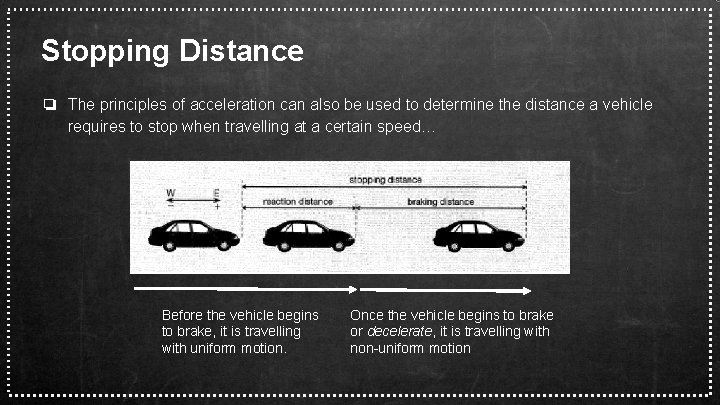
Stopping Distance ❏ The principles of acceleration can also be used to determine the distance a vehicle requires to stop when travelling at a certain speed… Before the vehicle begins to brake, it is travelling with uniform motion. Once the vehicle begins to brake or decelerate, it is travelling with non-uniform motion

1) Calculating Stopping Distance Calculate the distance travelled while the driver reacts (i. e. the distance travelled while moving with uniform motion). . . V = d/t so d = (v)(t) 2) Calculate the distance travelled once the driver starts braking (i. e. the distance travelled while moving with nonuniform motion). . . Before the vehicle begins to brake, it is travelling with uniform motion. Step 1 Step 2 Once the vehicle begins to brake or decelerate, it is travelling with non-uniform motion ● First use the rate of deceleration given to calculate the time required to stop: - vi) /a ● a = (vf - vi) / t so t = (vf Then use the time required to stop, initial, and final velocity of the vehicle provided to determine its displacement: d = [(vi + vf) / 2] (t)

Calculating Stopping Distance EXAMPLE The typical reaction time for most drivers is about 1. 50 s. A vehicle travelling under typical conditions is able to decelerate at a rate of -5. 85 m/s 2. Determine the minimum stopping distance of a vehicle travelling at a velocity of +110 km/h. Before the vehicle begins to brake, it is travelling with uniform motion. Step 1 Step 2 Once the vehicle begins to brake or decelerate, it is travelling with non-uniform motion