Tomography and Reconstruction Lecture Overview Applications Backgroundhistory of

Tomography and Reconstruction Lecture Overview • Applications • Background/history of tomography • Measurement of Projection data • Example of flame tomography • Radon Transform • Fourier Slice Theorem • Filtered Back Projection • Algebraic techniques School of Engineering

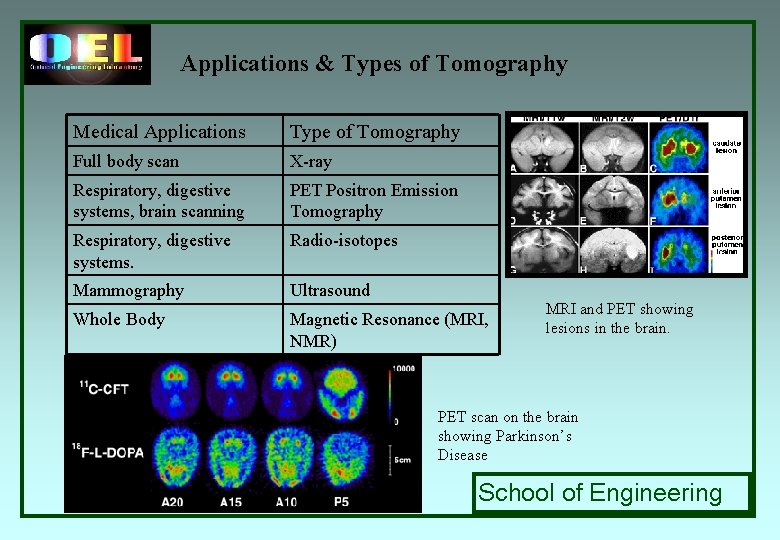
Applications & Types of Tomography Medical Applications Type of Tomography Full body scan X-ray Respiratory, digestive systems, brain scanning PET Positron Emission Tomography Respiratory, digestive systems. Radio-isotopes Mammography Ultrasound Whole Body Magnetic Resonance (MRI, NMR) MRI and PET showing lesions in the brain. PET scan on the brain showing Parkinson’s Disease School of Engineering

Applications & Types of Tomography Non Medical Applications Type of Tomography Oil Pipe Flow Turbine Plumes Flame Analysis Resistive/Capacitance Tomography Optical Tomography ECT on industrial pipe flows School of Engineering

The History • Johan Radon (1917) showed how a reconstruction from projections was possible. • Cormack (1963, 1964) introduced Fourier transforms into the reconstruction algorithms. • Hounsfield (1972) invented the X-ray Computer scanner for medical work, (which Cormack and Hounsfield shared a Nobel prize). • EMI Ltd (1971) announced development of the EMI scanner which combined X-ray measurements and sophisticated algorithms solved by digital computers. School of Engineering

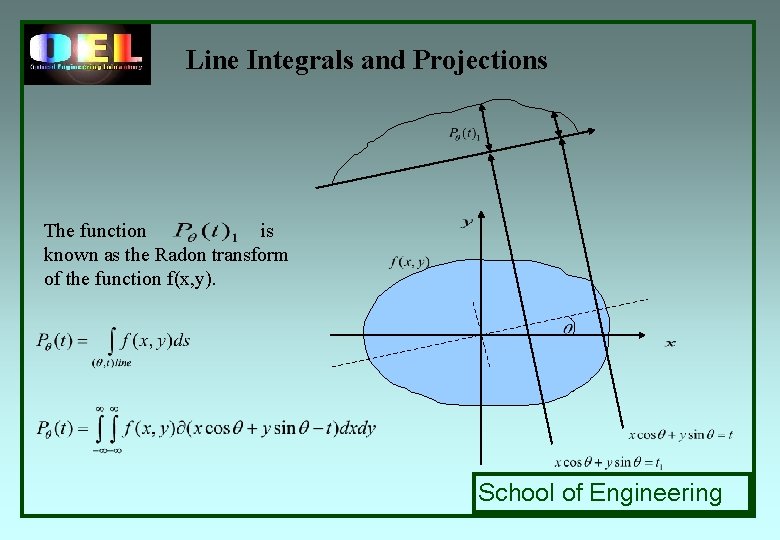
Line Integrals and Projections The function is known as the Radon transform of the function f(x, y). School of Engineering

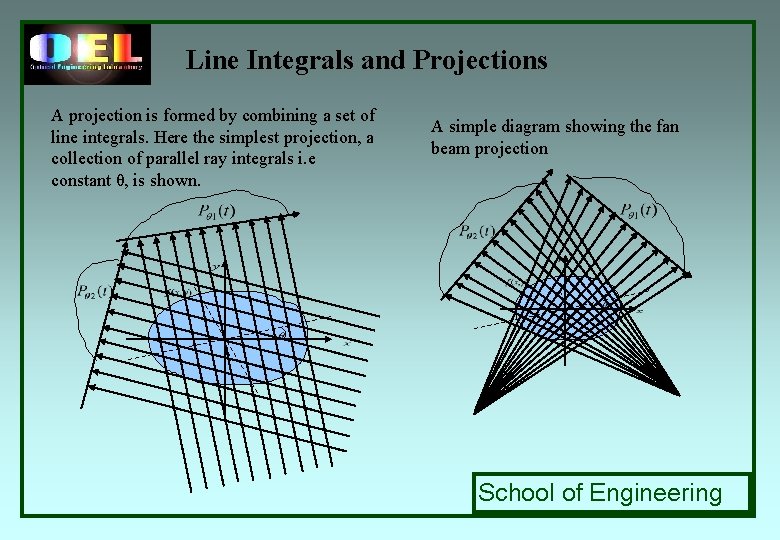
Line Integrals and Projections A projection is formed by combining a set of line integrals. Here the simplest projection, a collection of parallel ray integrals i. e constant θ, is shown. A simple diagram showing the fan beam projection School of Engineering

Fourier Slice Theorem The Fourier slice theorem is derived by taking the one-dimensional Fourier transform of a parallel projection and noting that it is equal to a slice of the two-dimensional Fourier transform of the original object. It follows that given the projection data, it should then be possible to estimate the object by simply performing the 2 D inverse Fourier transform. Start by defining the 2 D Fourier transform of the object function as The part in brackets is the equation for a projection along lines of constant x Define the projection at angle θ, Pθ(t) and its transform by For simplicity θ=0 which leads to v=0 As the phase factor is no-longer dependent on y, the integral can be split. Substituting in Thus the following relationship between the vertical projection and the 2 D transform of the object function: School of Engineering

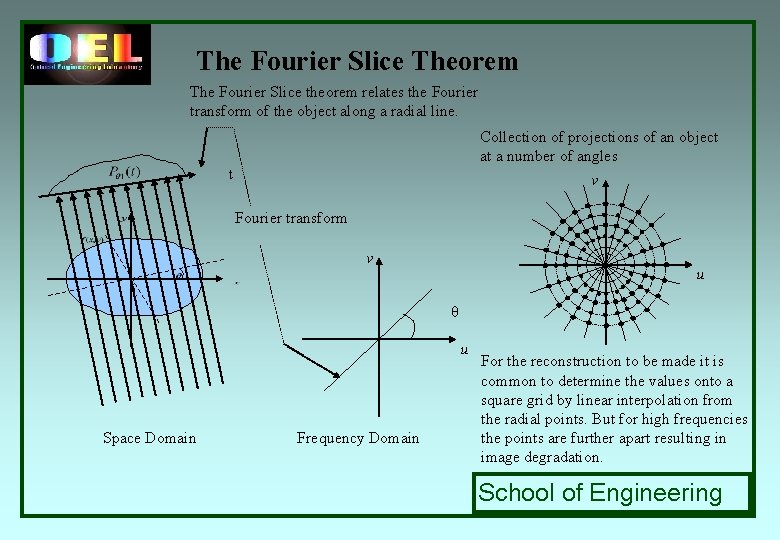
The Fourier Slice Theorem The Fourier Slice theorem relates the Fourier transform of the object along a radial line. Collection of projections of an object at a number of angles t v Fourier transform v u θ u Space Domain Frequency Domain For the reconstruction to be made it is common to determine the values onto a square grid by linear interpolation from the radial points. But for high frequencies the points are further apart resulting in image degradation. School of Engineering

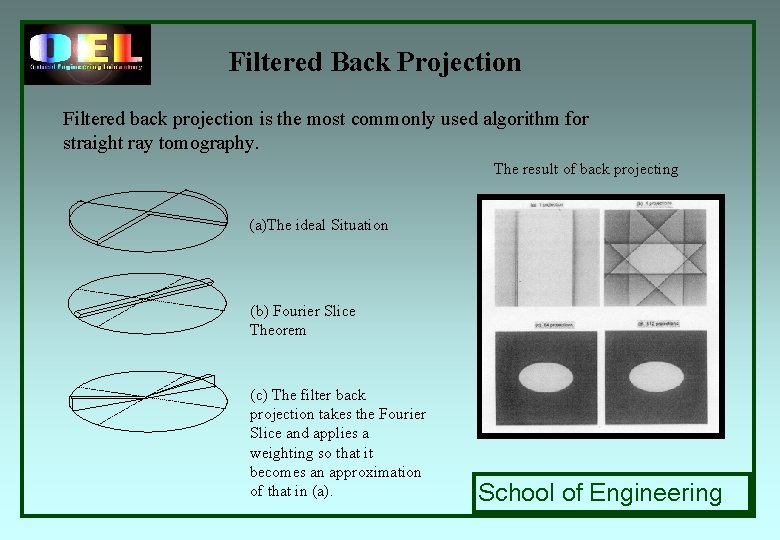
Filtered Back Projection Filtered back projection is the most commonly used algorithm for straight ray tomography. The result of back projecting (a)The ideal Situation (b) Fourier Slice Theorem (c) The filter back projection takes the Fourier Slice and applies a weighting so that it becomes an approximation of that in (a). School of Engineering

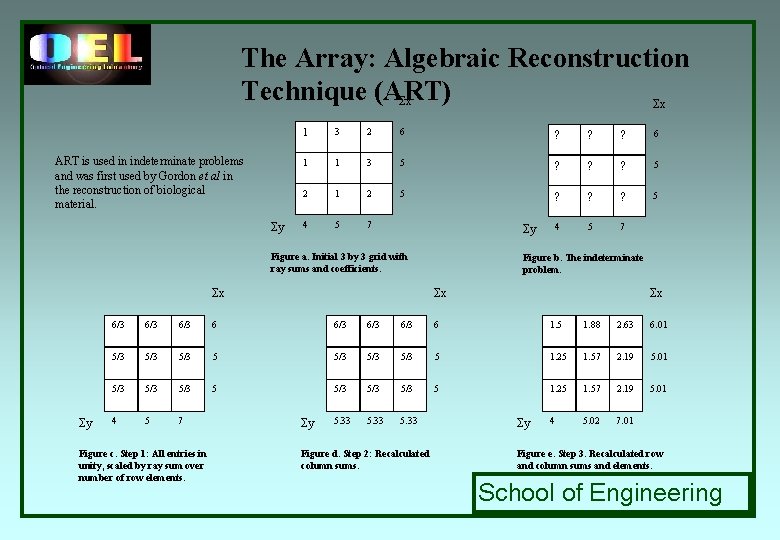
The Array: Algebraic Reconstruction Technique (ART) Σx Σx ART is used in indeterminate problems and was first used by Gordon et al in the reconstruction of biological material. Σy 1 3 2 6 ? ? ? 6 1 1 3 5 ? ? ? 5 2 1 2 5 ? ? ? 5 4 5 7 Σy Figure a. Initial 3 by 3 grid with ray sums and coefficients. Σx Σy Figure b. The indeterminate problem. Σx Σx 6/3 6/3 6/3 6 1. 5 1. 88 2. 63 6. 01 5/3 5/3 5/3 5 1. 25 1. 57 2. 19 5. 01 4 5 7 5. 33 4 5. 02 7. 01 Figure c. Step 1: All entries in unity, scaled by ray sum over number of row elements. Σy Figure d. Step 2: Recalculated column sums. Σy Figure e. Step 3. Recalculated row and column sums and elements. School of Engineering

Measurement of projection data Attenuation of X-rays Assume no loss of intensity of the beam due to divergence, however the beam does attenuate due to photons either being absorbed or scattered by the object. Photoelectric Absorption Compton Scattering This consists of an x-ray photon imparting all of its energy to an inner electron of an atom. The electron uses this energy to overcome the binding energy within its shell, and the rest appearing as kinetic energy in this freed electron. This consists of the interaction of the photon with either the free electron or a loosely bound outer shell electron. As a result the x-ray is deflected from its original direction. School of Engineering

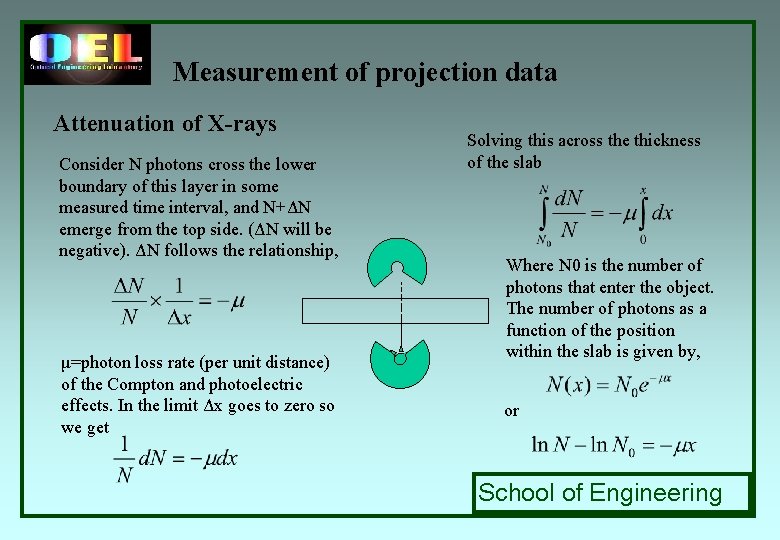
Measurement of projection data Attenuation of X-rays Consider N photons cross the lower boundary of this layer in some measured time interval, and N+ΔN emerge from the top side. (ΔN will be negative). ΔN follows the relationship, μ=photon loss rate (per unit distance) of the Compton and photoelectric effects. In the limit Δx goes to zero so we get Solving this across the thickness of the slab Where N 0 is the number of photons that enter the object. The number of photons as a function of the position within the slab is given by, or School of Engineering

Flame Thickness, Emission and Absorption Fibre optic to spectrograph Mercury lamp Transmitted portion of back light radiation, L 2 Burner Interpretation of Results Transmitted portion of backlight radiation, L 2: Radiation incident on fibre from backlight, L 1: 72% transmission at 309 nm Optical thickness at 309 nm, Radiant intensity of backlight, L 1 11. 53 counts 16. 06 counts Absorption Coefficient: Radiance emitted by gas, L 3 Signal leaving flame Signal entering flame Optical arrangement used to determine the optical thickness of a flame. Emission Coefficient: Background Lamp, L 1 Flame, L 3 Flame+Lamp, L Counts 77. 71 93. 76 439. 29 450. 82 Minus Background - 16. 06 361. 59 373. 12 School of Engineering

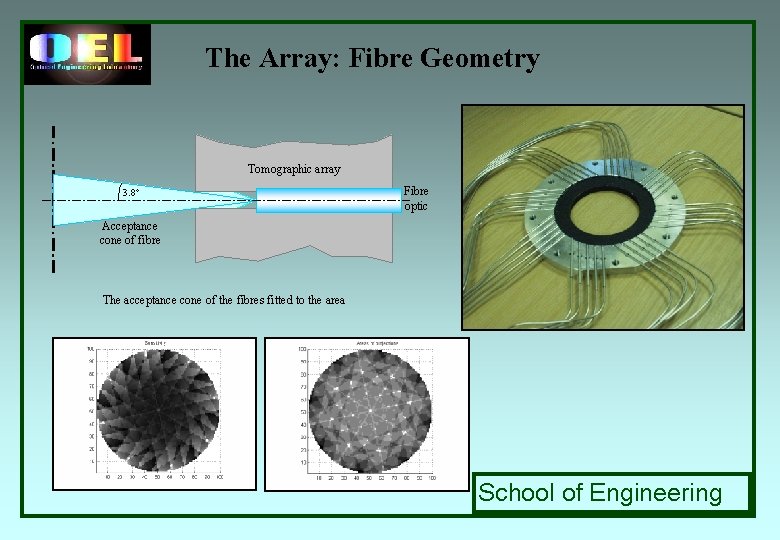
The Array: Fibre Geometry Tomographic array 3. 8 Fibre optic Acceptance cone of fibre The acceptance cone of the fibres fitted to the area School of Engineering

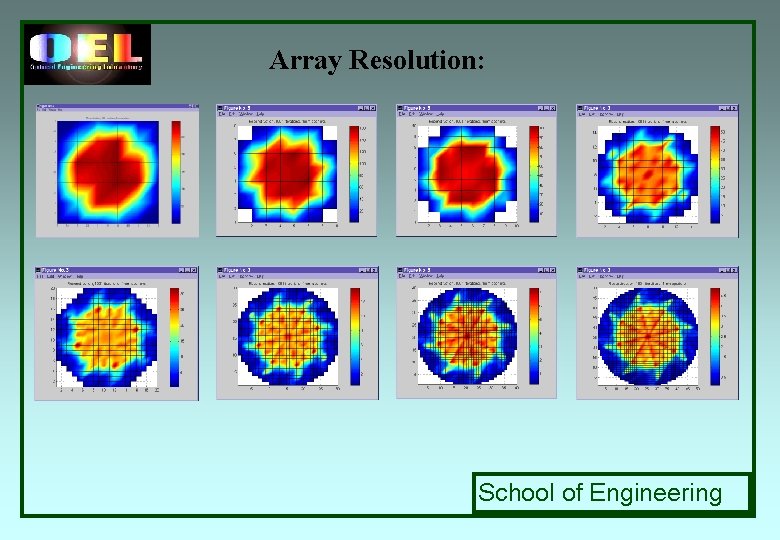
Array Resolution: School of Engineering

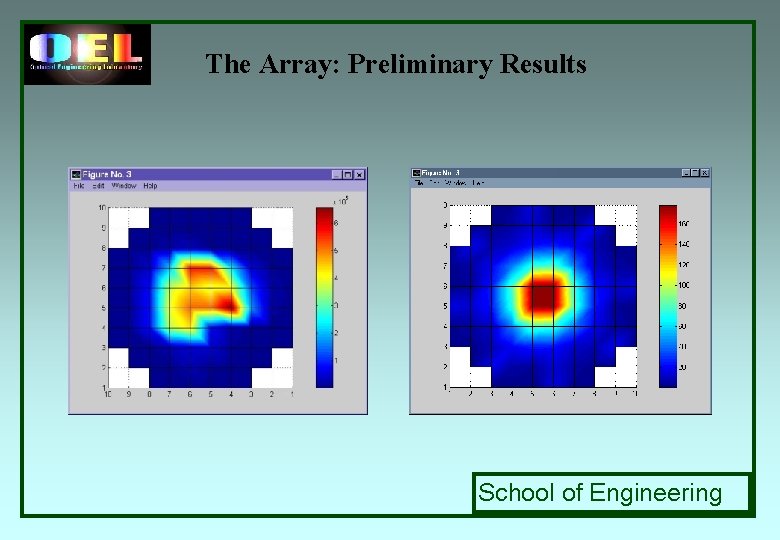
The Array: Preliminary Results School of Engineering

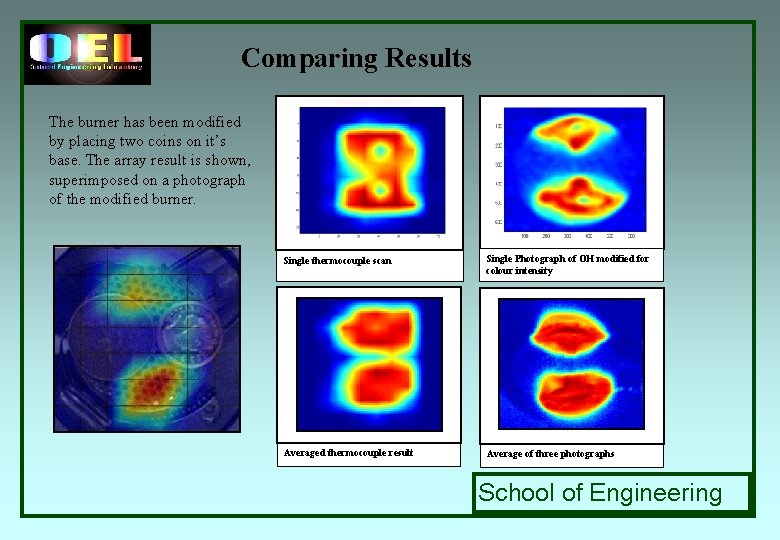
Comparing Results The burner has been modified by placing two coins on it’s base. The array result is shown, superimposed on a photograph of the modified burner. Single thermocouple scan Single Photograph of OH modified for colour intensity Averaged thermocouple result Average of three photographs School of Engineering