Tomasz Michaek HIGH RAYLEIGH NUMBER NATURAL CONVECTION IN

Tomasz Michałek HIGH RAYLEIGH NUMBER NATURAL CONVECTION IN A CUBIC ENCLOSURE Institute of Fundamental Technological Research Polish Academy of Sciences, Dept. of Mechanics and Physics of Fluids, Poland.

Outline 1. Experimental benchmark – – Sensitivity Analysis Towards Benchmark Definition Experimental measurements Results for moderate Ra Numbers Experimental Benchmark (Ra = 1. 5*106, Pr =11. 78) 2. Towards high Ra Numbers and transition regime – – 2 D full velocity & temperature fields Statistics of velocity fields Time series of velocities Validation of computational results

Building credibility to CFD results Verification Code/Program verification • Method of manufactured solution [Roache] Verification of Calculation • Richardson extrapolation (RE) Validation of Idealized problems Validation of actual configuration • Unit problems • Benchmark cases • Analytical solutions • Generalized RE [Stern at all. ] • Numerical benchmarks [Ghia, de Vahl Davis, Le Quere, …] • Simplified/Partial Flow Path • Grid Convergence Index (GCI) [Roache] • Actual Hardware [Sindir et al. ] sensitivity analysis

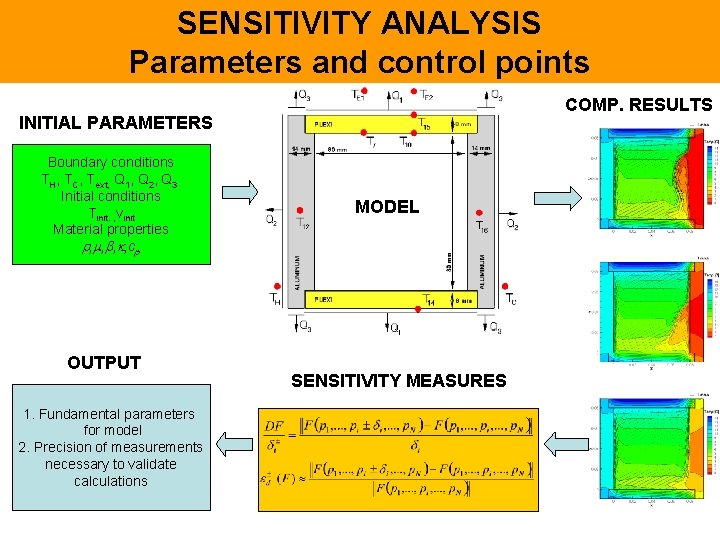
SENSITIVITY ANALYSIS Parameters and control points COMP. RESULTS INITIAL PARAMETERS Boundary conditions TH, TC, Text, Q 1, Q 2, Q 3 Initial conditions Tinit. , vinit Material properties , , cp OUTPUT 1. Fundamental parameters for model 2. Precision of measurements necessary to validate calculations MODEL SENSITIVITY MEASURES

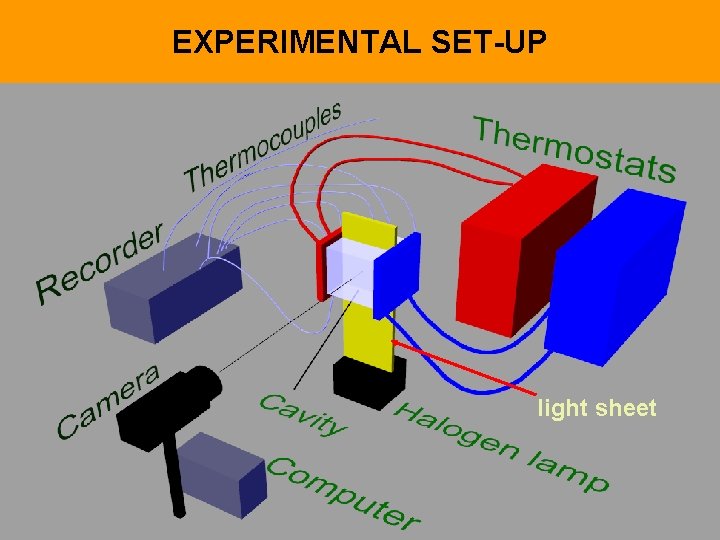
EXPERIMENTAL SET-UP light sheet

CAVITY DETAILS Control points for monitoring internal and external temperatures CENTRAL CROS-SECTION TE 1 TE 2 T 14 PLEXIGLASS WALL Tc WALL Th ALUMINIUM TL T 10 ALUMINIUM WALL T 7 PLEXIGLASS WALL T 15 TP

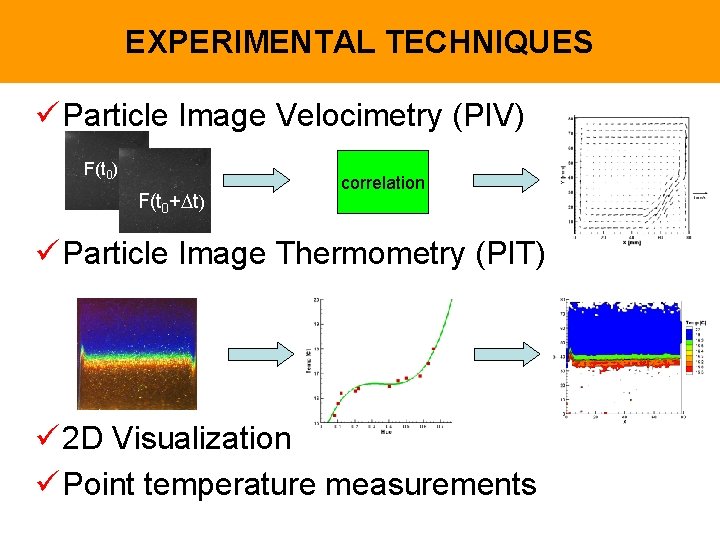
EXPERIMENTAL TECHNIQUES ü Particle Image Velocimetry (PIV) F(t 0+ t) correlation ü Particle Image Thermometry (PIT) ü 2 D Visualization ü Point temperature measurements

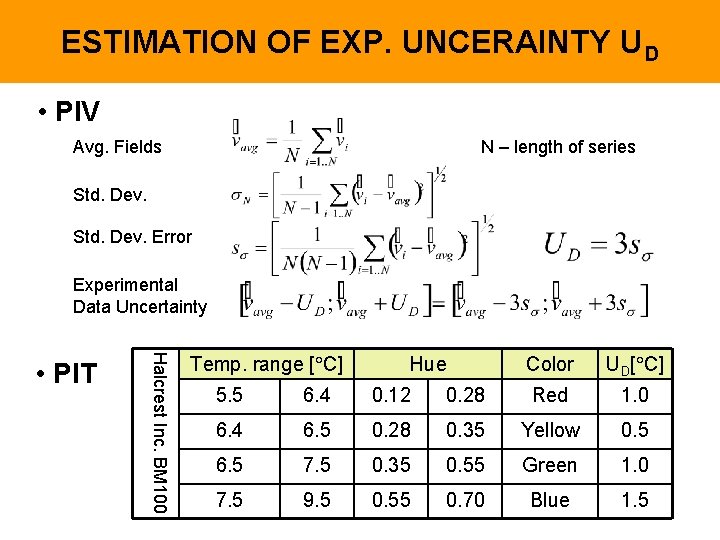
ESTIMATION OF EXP. UNCERAINTY UD • PIV Avg. Fields N – length of series Std. Dev. Error Experimental Data Uncertainty Halcrest Inc. BM 100 • PIT Temp. range [ C] Hue Color UD[ C] 5. 5 6. 4 0. 12 0. 28 Red 1. 0 6. 4 6. 5 0. 28 0. 35 Yellow 0. 5 6. 5 7. 5 0. 35 0. 55 Green 1. 0 7. 5 9. 5 0. 55 0. 70 Blue 1. 5

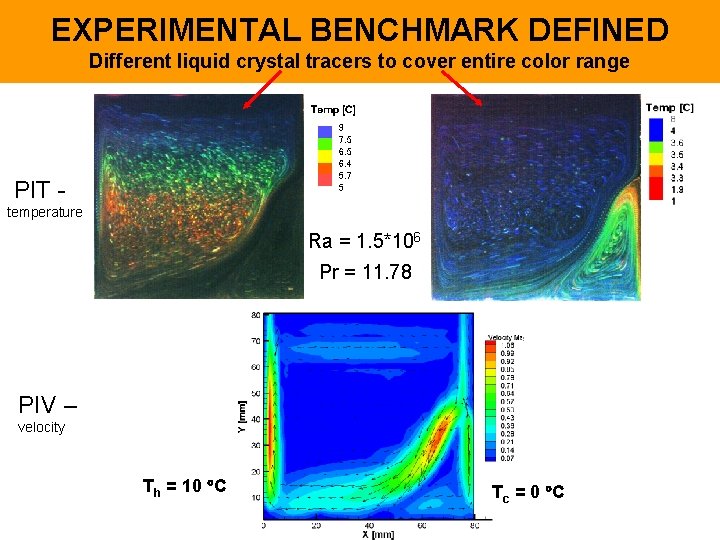
EXPERIMENTAL BENCHMARK DEFINED Different liquid crystal tracers to cover entire color range PIT temperature Ra = 1. 5*106 Pr = 11. 78 PIV – velocity Th = 10 C Tc = 0 C

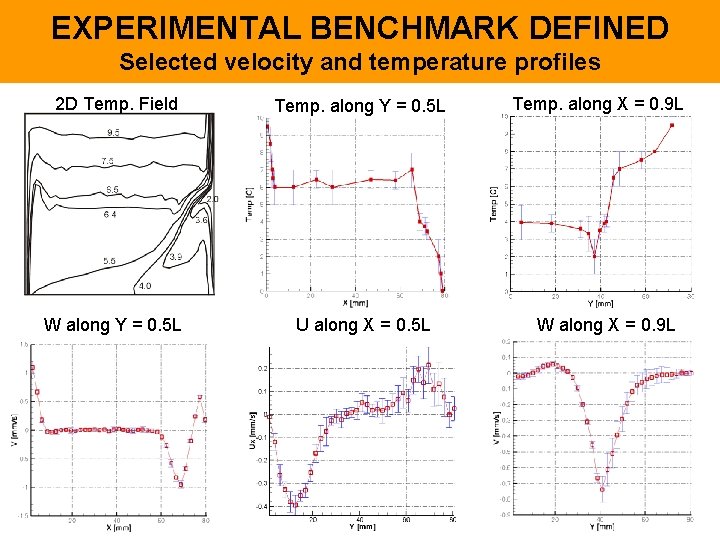
EXPERIMENTAL BENCHMARK DEFINED Selected velocity and temperature profiles 2 D Temp. Field Temp. along Y = 0. 5 L W along Y = 0. 5 L U along X = 0. 5 L Temp. along X = 0. 9 L W along X = 0. 9 L

EXPERIMENTAL UNCERTAINTY ESTIMATION N = 40, t = 1 s • PIV Temp. range [ C] Mix C • PIT two sets of tracers Hue Color UD[ C] BM 100 0. 0 3. 0 0. 11 0. 18 Red 1. 0 3. 5 0. 18 0. 25 Yellow 0. 5 3. 9 0. 25 0. 48 Green 0. 5 3. 9 8. 0 0. 48 0. 66 Blue 3. 0 5. 5 6. 4 0. 12 0. 28 Red 1. 0 6. 4 6. 5 0. 28 0. 35 Yellow 0. 5 6. 5 7. 5 0. 35 0. 55 Green 1. 0 7. 5 9. 5 0. 55 0. 70 Blue 1. 5

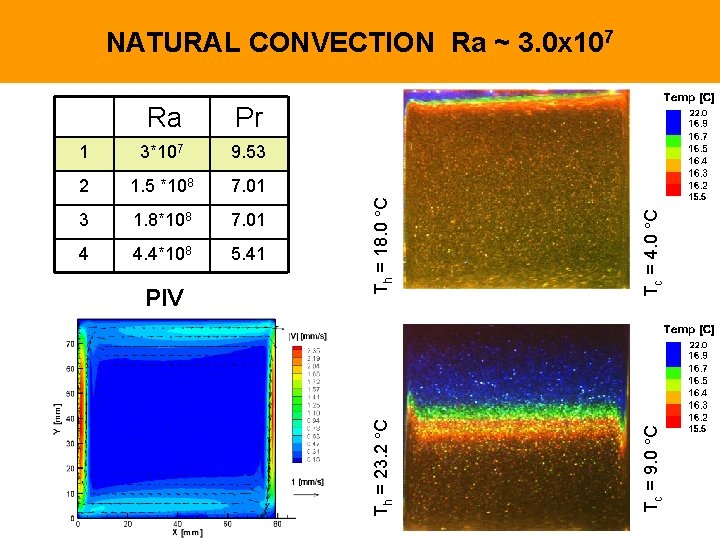
3*107 9. 53 2 1. 5 *108 7. 01 3 1. 8*108 7. 01 4 4. 4*108 5. 41 PIV Tc = 4. 0 C 1 Tc = 9. 0 C Pr Th = 18. 0 C Ra Th = 23. 2 C NATURAL CONVECTION Ra ~ 3. 0 x 107

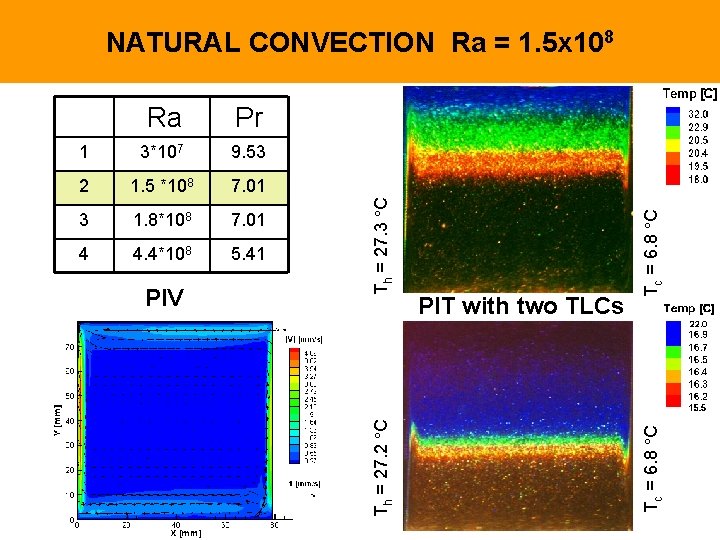
3*107 9. 53 2 1. 5 *108 7. 01 3 1. 8*108 7. 01 4 4. 4*108 5. 41 PIV PIT with two TLCs Tc = 6. 8 C 1 Tc = 6. 8 C Pr Th = 27. 2 C Ra Th = 27. 3 C NATURAL CONVECTION Ra = 1. 5 x 108

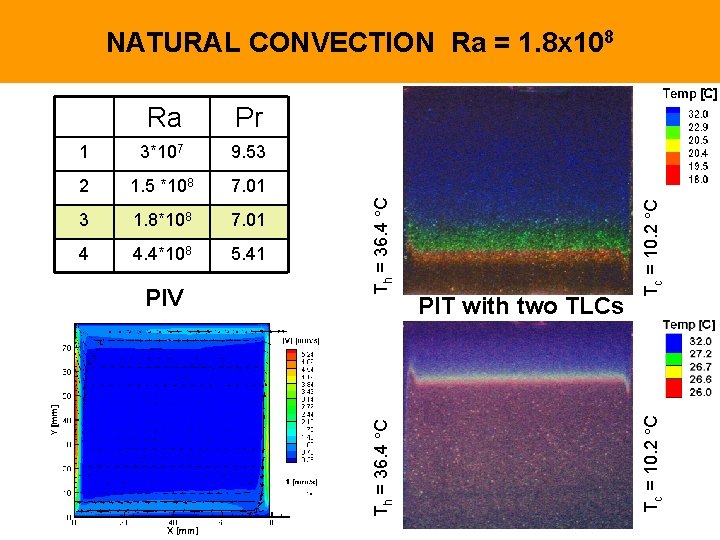
3*107 9. 53 2 1. 5 *108 7. 01 3 1. 8*108 7. 01 4 4. 4*108 5. 41 PIV PIT with two TLCs Tc = 10. 2 C 1 Tc = 10. 2 C Pr Th = 36. 4 C Ra Th = 36. 4 C NATURAL CONVECTION Ra = 1. 8 x 108

3*107 9. 53 2 1. 5 *108 7. 01 3 1. 8*108 7. 01 4 4. 4*108 5. 41 PIV PIT with two TLCs Tc = 14. 2 C 1 Tc = 14. 0 C Pr Th = 45. 8 C Ra Th = 45. 8 C NATURAL CONVECTION Ra = 4. 4 x 108

NATURAL CONVECTION AT HIGH RAYLEIGH NUMBER Ra = 3. 107 control points and area selected for velocity measurements Ra = 4. 4. 108

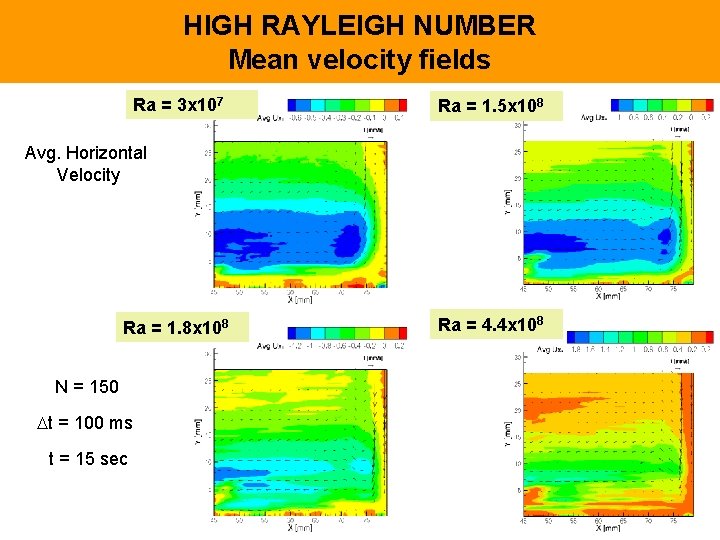
HIGH RAYLEIGH NUMBER Mean velocity fields Ra = 3 x 107 Ra = 1. 5 x 108 Avg. Horizontal Velocity Ra = 1. 8 x 108 N = 150 t = 100 ms t = 15 sec Ra = 4. 4 x 108

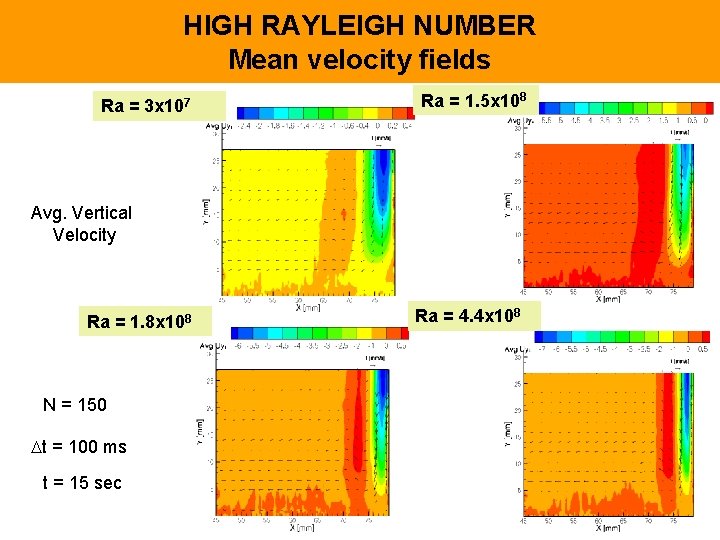
HIGH RAYLEIGH NUMBER Mean velocity fields Ra = 3 x 107 Ra = 1. 5 x 108 Avg. Vertical Velocity Ra = 1. 8 x 108 N = 150 t = 100 ms t = 15 sec Ra = 4. 4 x 108

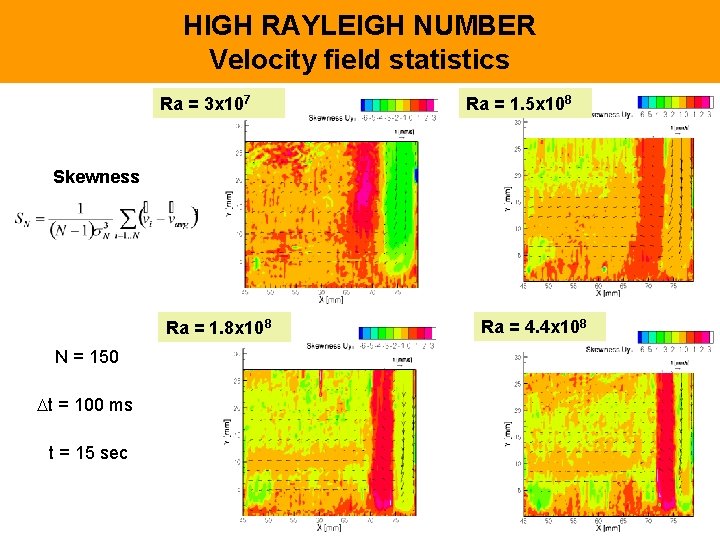
HIGH RAYLEIGH NUMBER Velocity field statistics Ra = 3 x 107 Ra = 1. 5 x 108 Skewness Ra = 1. 8 x 108 N = 150 t = 100 ms t = 15 sec Ra = 4. 4 x 108

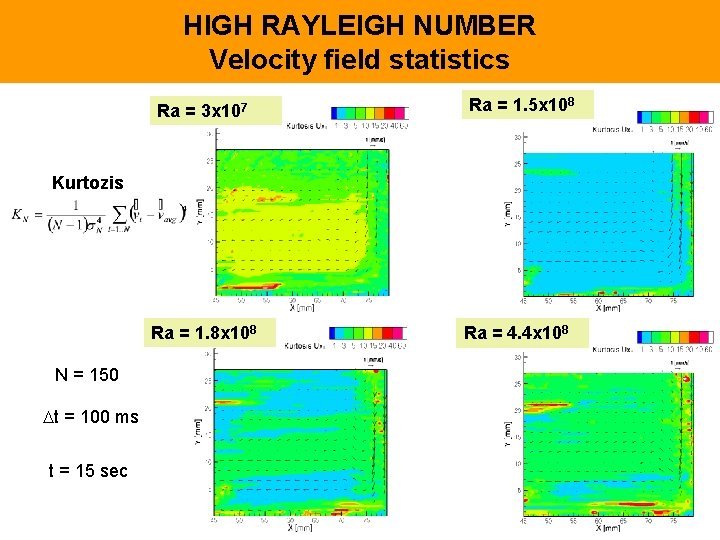
HIGH RAYLEIGH NUMBER Velocity field statistics Ra = 3 x 107 Ra = 1. 5 x 108 Kurtozis Ra = 1. 8 x 108 N = 150 t = 100 ms t = 15 sec Ra = 4. 4 x 108

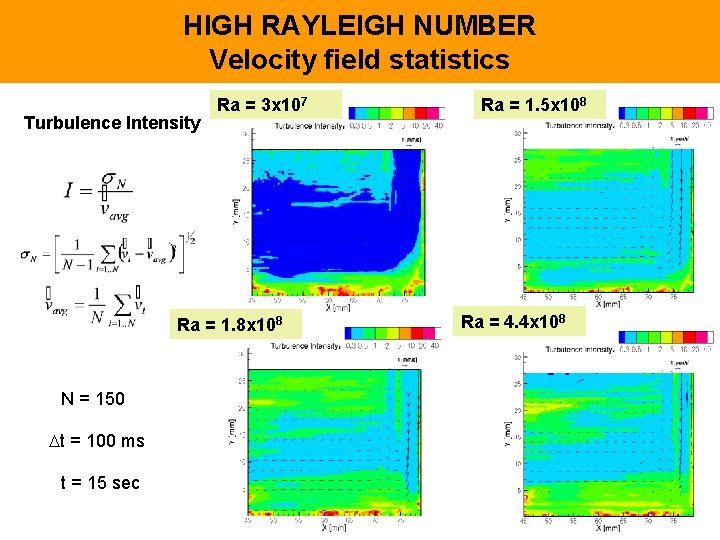
HIGH RAYLEIGH NUMBER Velocity field statistics Turbulence Intensity Ra = 3 x 107 Ra = 1. 8 x 108 N = 150 t = 100 ms t = 15 sec Ra = 1. 5 x 108 Ra = 4. 4 x 108

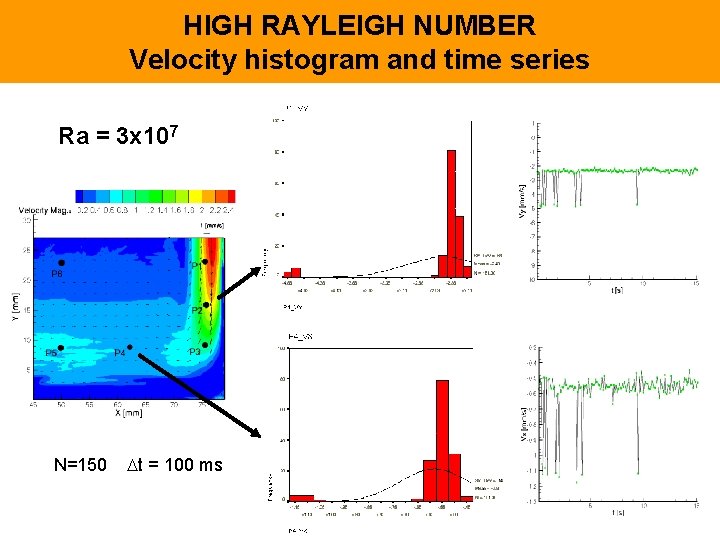
HIGH RAYLEIGH NUMBER Velocity histogram and time series Ra = 3 x 107 N=150 t = 100 ms

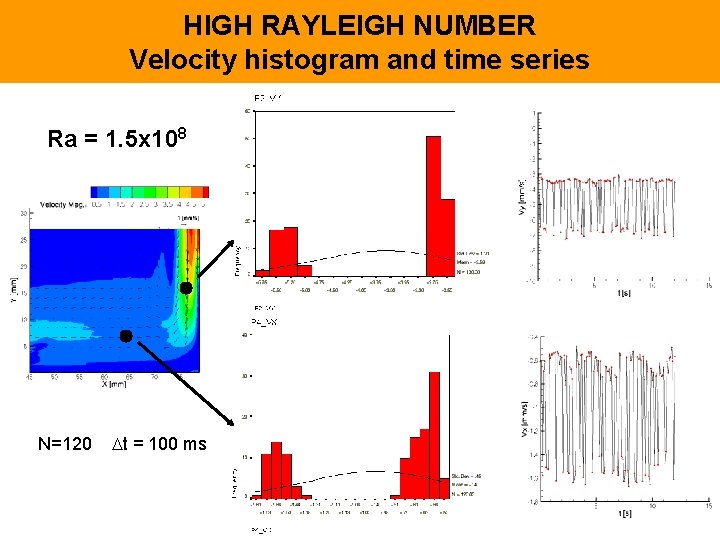
HIGH RAYLEIGH NUMBER Velocity histogram and time series Ra = 1. 5 x 108 N=120 t = 100 ms

HIGH RAYLEIGH NUMBER Velocity histogram and time series Ra = 1. 8 x 108 N=134 t = 100 ms

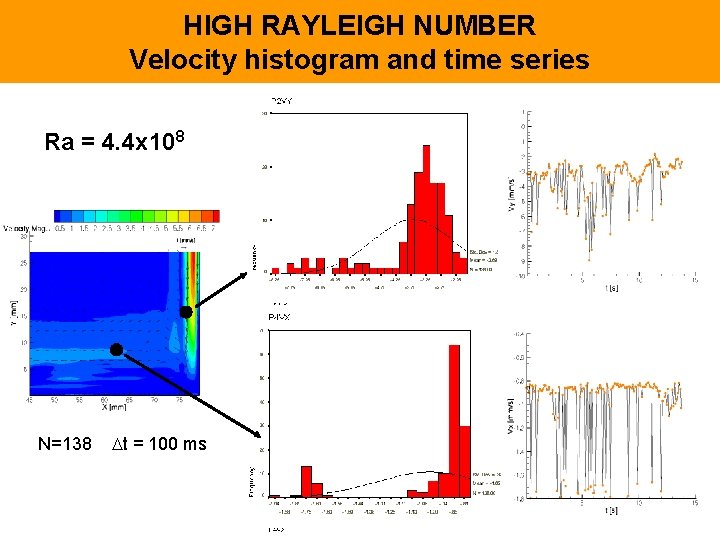
HIGH RAYLEIGH NUMBER Velocity histogram and time series Ra = 4. 4 x 108 N=138 t = 100 ms

VALIDATION METHODOLOGY Stern et all. , Comprehensive approach to verification and validation of CFD simulations – Part 1: Methodology and procedures Journal of Fluids Engineering – Transactions of ASME, 123 (4), pp. 793 -802, 2001. • Validation error • Validation metric In our examples: for water

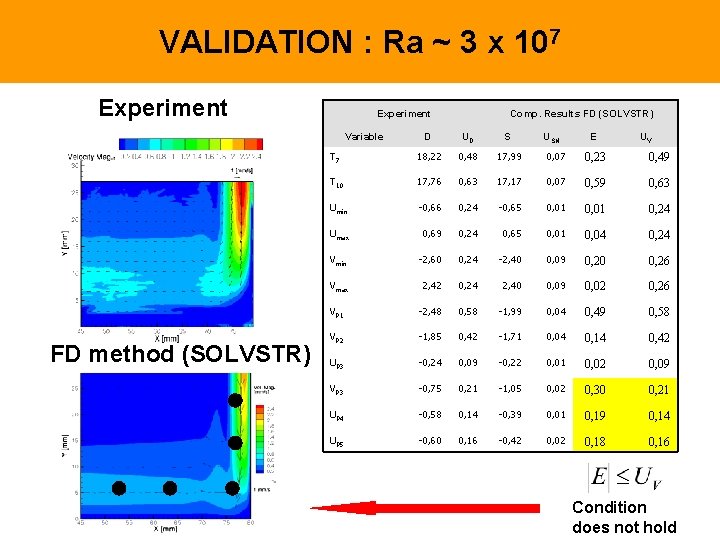
VALIDATION : Ra ~ 3 x 107 Experiment Variable FD method (SOLVSTR) Comp. Results FD (SOLVSTR) D UD S USN E UV T 7 18, 22 0, 48 17, 99 0, 07 0, 23 0, 49 T 10 17, 76 0, 63 17, 17 0, 07 0, 59 0, 63 Umin -0, 66 0, 24 -0, 65 0, 01 0, 24 Umax 0, 69 0, 24 0, 65 0, 01 0, 04 0, 24 Vmin -2, 60 0, 24 -2, 40 0, 09 0, 20 0, 26 Vmax 2, 42 0, 24 2, 40 0, 09 0, 02 0, 26 VP 1 -2, 48 0, 58 -1, 99 0, 04 0, 49 0, 58 VP 2 -1, 85 0, 42 -1, 71 0, 04 0, 14 0, 42 UP 3 -0, 24 0, 09 -0, 22 0, 01 0, 02 0, 09 VP 3 -0, 75 0, 21 -1, 05 0, 02 0, 30 0, 21 UP 4 -0, 58 0, 14 -0, 39 0, 01 0, 19 0, 14 UP 5 -0, 60 0, 16 -0, 42 0, 02 0, 18 0, 16 Condition does not hold

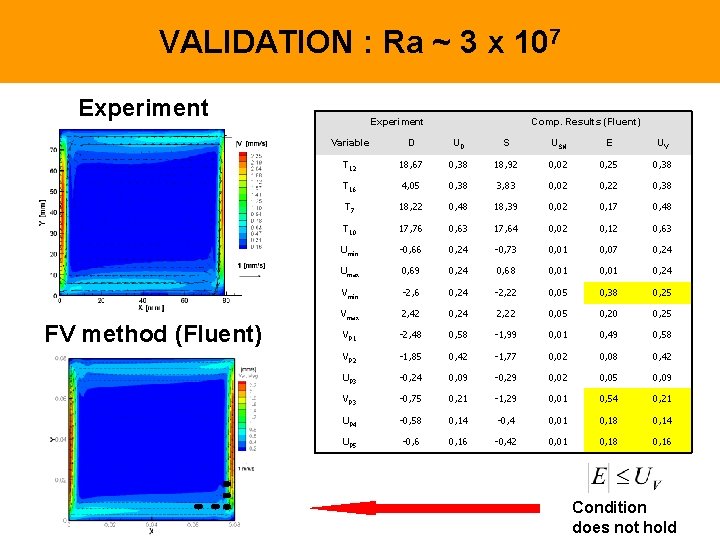
VALIDATION : Ra ~ 3 x 107 Experiment FV method (Fluent) Experiment Comp. Results (Fluent) Variable D UD S USN E UV T 12 18, 67 0, 38 18, 92 0, 02 0, 25 0, 38 T 16 4, 05 0, 38 3, 83 0, 02 0, 22 0, 38 T 7 18, 22 0, 48 18, 39 0, 02 0, 17 0, 48 T 10 17, 76 0, 63 17, 64 0, 02 0, 12 0, 63 Umin -0, 66 0, 24 -0, 73 0, 01 0, 07 0, 24 Umax 0, 69 0, 24 0, 68 0, 01 0, 24 Vmin -2, 6 0, 24 -2, 22 0, 05 0, 38 0, 25 Vmax 2, 42 0, 24 2, 22 0, 05 0, 20 0, 25 VP 1 -2, 48 0, 58 -1, 99 0, 01 0, 49 0, 58 VP 2 -1, 85 0, 42 -1, 77 0, 02 0, 08 0, 42 UP 3 -0, 24 0, 09 -0, 29 0, 02 0, 05 0, 09 VP 3 -0, 75 0, 21 -1, 29 0, 01 0, 54 0, 21 UP 4 -0, 58 0, 14 -0, 4 0, 01 0, 18 0, 14 UP 5 -0, 6 0, 16 -0, 42 0, 01 0, 18 0, 16 Condition does not hold

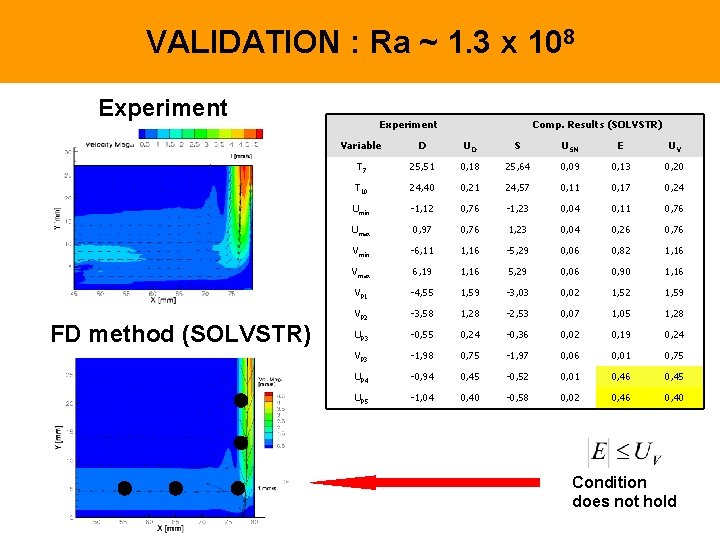
VALIDATION : Ra ~ 1. 3 x 108 Experiment FD method (SOLVSTR) Experiment Comp. Results (SOLVSTR) Variable D UD S USN E UV T 7 25, 51 0, 18 25, 64 0, 09 0, 13 0, 20 T 10 24, 40 0, 21 24, 57 0, 11 0, 17 0, 24 Umin -1, 12 0, 76 -1, 23 0, 04 0, 11 0, 76 Umax 0, 97 0, 76 1, 23 0, 04 0, 26 0, 76 Vmin -6, 11 1, 16 -5, 29 0, 06 0, 82 1, 16 Vmax 6, 19 1, 16 5, 29 0, 06 0, 90 1, 16 VP 1 -4, 55 1, 59 -3, 03 0, 02 1, 59 VP 2 -3, 58 1, 28 -2, 53 0, 07 1, 05 1, 28 UP 3 -0, 55 0, 24 -0, 36 0, 02 0, 19 0, 24 VP 3 -1, 98 0, 75 -1, 97 0, 06 0, 01 0, 75 UP 4 -0, 94 0, 45 -0, 52 0, 01 0, 46 0, 45 UP 5 -1, 04 0, 40 -0, 58 0, 02 0, 46 0, 40 Condition does not hold

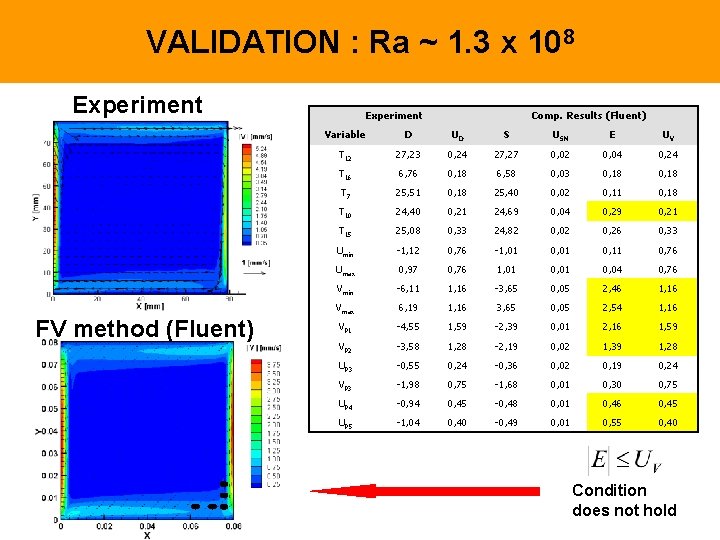
VALIDATION : Ra ~ 1. 3 x 108 Experiment FV method (Fluent) Experiment Comp. Results (Fluent) Variable D UD S USN E UV T 12 27, 23 0, 24 27, 27 0, 02 0, 04 0, 24 T 16 6, 76 0, 18 6, 58 0, 03 0, 18 T 7 25, 51 0, 18 25, 40 0, 02 0, 11 0, 18 T 10 24, 40 0, 21 24, 69 0, 04 0, 29 0, 21 T 15 25, 08 0, 33 24, 82 0, 02 0, 26 0, 33 Umin -1, 12 0, 76 -1, 01 0, 11 0, 76 Umax 0, 97 0, 76 1, 01 0, 04 0, 76 Vmin -6, 11 1, 16 -3, 65 0, 05 2, 46 1, 16 Vmax 6, 19 1, 16 3, 65 0, 05 2, 54 1, 16 VP 1 -4, 55 1, 59 -2, 39 0, 01 2, 16 1, 59 VP 2 -3, 58 1, 28 -2, 19 0, 02 1, 39 1, 28 UP 3 -0, 55 0, 24 -0, 36 0, 02 0, 19 0, 24 VP 3 -1, 98 0, 75 -1, 68 0, 01 0, 30 0, 75 UP 4 -0, 94 0, 45 -0, 48 0, 01 0, 46 0, 45 UP 5 -1, 04 0, 40 -0, 49 0, 01 0, 55 0, 40 Condition does not hold

CONCLUSIONS The sensitivity analysis was used to identify fundamental (crucial) parameters for considered configuration. Experimental benchmark was defined for moderate Ra numbers. Agreement between computational results and experimental data was achieved. 2 D Temperature fields, 2 D Velocity fields were determined for high Ra numbers in the central cross-section of the box cavity heated from the side. Uncertainty of experimental data was assessed. Velocity fluctuations were observed in these experiments for high Ra number below Rac. Numerical simulations were performed for Ra = 3 x 107, 1. 3 x 108 (FV, FD). Validation procedure was performed in order to assess modeling errors. Velocity fluctuations were not reproduced by computational results. These fluctuations were attributed to non-uniformity of thermal boundary conditions along the bottom wall.

Thank you for your attention!