Toma de Decisiones Toda toma de decisin empieza

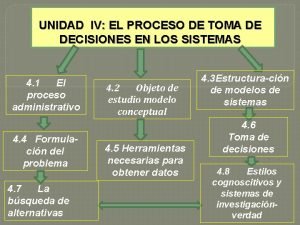
Toma de Decisiones Toda toma de decisión empieza con la detección de un problema. Para tomar la decisión correcta, se debe: Definir el problema en forma clara Formular el o los objetivos Identificar las restricciones Identificar las alternativas de solución Evaluar las alternativas y elegir la mejor

Toma de Decisiones ¿Como se elige la mejor alternativa? Métodos Cualitativos En base a la experiencia y al juicio profesional de la persona que toma la decisión Métodos Cuantitativos En base a la utilización de herramientas matemáticas que permitan maximizar la efectividad en la toma de decisiones.

Investigación de Operaciones La dificultad de tomar decisiones ha hecho que el hombre se aboque en la búsqueda de una herramienta o método que le permita tomar las mejores decisiones de acuerdo a los recursos disponibles y a los objetivos que persigue. Este conjunto de herramientas o métodos es lo que llamaremos Investigación de Operaciones. Definición más formal “Enfoque científico de la toma de decisiones que requiere la operación de sistemas organizacionales”. La IO nos ofrece una serie de herramientas cuantitativas para la toma de decisiones.

Investigación de Operaciones Para la aplicación de la IO se siguen los siguientes pasos: • La IO comienza con la observación cuidadosa de la realidad. • Formular el problema. • Construir un modelo que intente abstraer la esencia del problema real. • Solución del modelo. • Análisis de sensibilidad, hay que ver como se comporta el modelo ante cambios en las restricciones y/o parámetros del modelo • Implementar los resultados, se debe interpretar los resultados y dar conclusiones y cursos de acción para la optimización del problema real

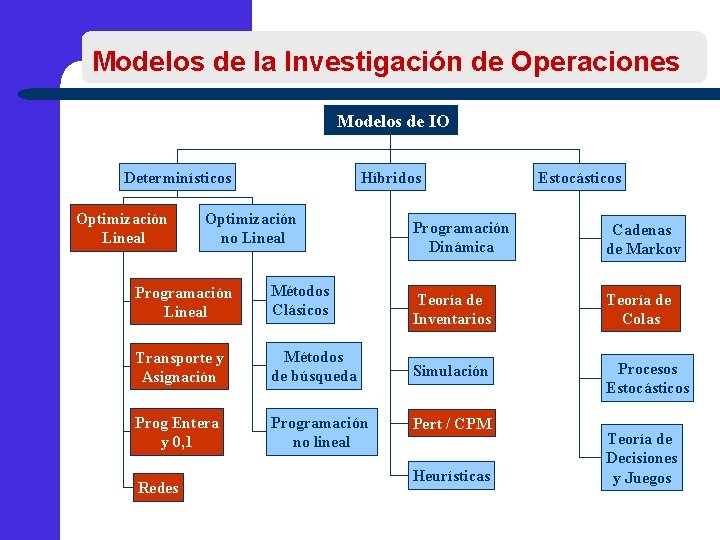
Modelos de la Investigación de Operaciones Modelos de IO Determinísticos Optimización Lineal Híbridos Optimización no Lineal Programación Lineal Métodos Clásicos Transporte y Asignación Métodos de búsqueda Prog Entera y 0, 1 Programación no lineal Redes Estocásticos Programación Dinámica Cadenas de Markov Teoría de Inventarios Teoría de Colas Simulación Procesos Estocásticos Pert / CPM Heurísticas Teoría de Decisiones y Juegos

Programación Lineal FO: Max o Min Z = C X Sujeto a AX B Xj 0 ; j = 1, 2, . . , n La Programación Lineal es una herramienta para resolver problemas de optimización que se caracterizan por tener como función objetivo y restricciones combinaciones lineales de las variables de decisión. Conceptos Básicos: • Variables de Decisión • Función Objetivo • Restricciones de Signo

Programación Lineal Consideremos el siguiente ejemplo para describir los conceptos básicos presentes en todo problema de programación lineal (PPL) 1. - Una mueblería produce mesas y sillas de madera. Cada mesa es vendida en $27. 000 y se requiere $10. 000 en materiales para su construcción, además, el costo unitario por mano de obra es de $14. 000. En el caso de las sillas, el precio de venta es de $21. 000 y los costos de materiales y mano de obra son $9. 000 y $10. 000 respectivamente. La fabricación de cada producto requiere de dos labores: carpintería y terminaciones. Una mesa requiere de 1 hora de carpintería y 2 de terminaciones, mientras que la silla requiere de 1 hora en cada labor.

Programación Lineal Cada semana, la mueblería puede obtener todos los materiales que desee, sin embargo, se pueden dedicar hasta 100 horas a las terminaciones y hasta 80 horas a la carpintería. La demanda por mesas no está limitada, mientras que la demanda por sillas es de 40 unidades. Formule un modelo matemático que permita maximizar las utilidades de la mueblería. Variables de decisión: Se debe comenzar definiendo las variables de decisión relevantes. En un PPL las variables de decisión deben ser capaces de describir completamente las decisiones que puedan ser tomadas y todas las variantes que existan.

Programación Lineal Antes de definir las variables de decisión es importante definir las unidades involucradas en el problema. En este caso, se habla de unidades de sillas y mesas, de horas de trabajo por unidad y de demanda semanal. De acuerdo a ello, una buena opción para definir las variables de decisión consiste en asociar las variables al número de unidades de sillas y mesas a producir por semana. Por lo tanto, podemos definir: X 1 = Número de mesas producidas por semana. X 2 = Número de sillas producidas por semana.

Programación Lineal Función Objetivo: En un PPL, se debe tomar la decisión de maximizar (usualmente las utilidades) o de minimizar (usualmente los costos) cierta función de las variables de decisión. La función que se va a optimizar se llama Función Objetivo (FO) y en ella no aparece ningún término independiente o constante. Los valores de las variables de decisión son independientes de cualquier constante. En el ejemplo, los costos e ingresos no dependen del valor de X 1 o X 2 por lo tanto basta concentrarse en maximizar la diferencia entre: Ingresos Semanales – Costos de Materiales – Costos por mano de obra

Programación Lineal Luego se deben expresar los términos anteriores en función de las variables de decisión X 1 y X 2. Por lo que la función objetivo queda (expresada en miles de $): (27 X 1 + 21 X 2) – (10 X 1 + 9 X 2) – (14 X 1 + 10 X 2) = 3 X 1 + 2 X 2 Así, el objetivo de la mueblería es escoger los valores X 1 y X 2 tal que se maximice 3 X 1 + 2 X 2 Denotando por Z el valor de la FO para cualquier PPL, la función de la mueblería es: Max Z = 3 X 1 + 2 X 2 El coeficiente que acompaña a cada variable en la FO se denomina coeficiente en la función objetivo de la variable y refleja el aporte unitario de dicha variable a la función objetivo

Programación Lineal Restricciones: En las medidas que las variables crecen, la FO aumenta su valor. Por lo tanto si se pudiera escoger arbitrariamente el valor de la variables, la mueblería podría hacer crecer el valor de sus utilidades en forma infinita. En la práctica esto no es posible y en el ejemplo el valor que toman las variables está limitado por las siguientes 3 restricciones: • Máximo 100 horas semanales para terminaciones. • Máximo 80 horas semanales para carpintería. • Producción máxima de 40 sillas semanales. Luego, el próximo paso consiste en formular matemáticamente las restricciones anteriores en función de las variables de decisión.

Programación Lineal Para formular la primera restricción en función de las variables X 1 y X 2 observamos que: Hrs. terminaciones x mesa + hrs. terminaciones x silla hrs. disponibles para terminación Por lo que la restricción queda: 2 X 1 + X 2 100 Es importante notar que todos los valores en la expresión anterior son por semana, ya que las variables de decisión se han escogido con esa referencia.

Programación Lineal Análogamente la segunda restricción queda: X 1 + X 2 80 Finalmente, la tercera restricción sólo limita el valor de la variable X 2 40 Restricciones de Signo: Para completar la formulación del modelo es importante definir si existe alguna restricción de signo para cada variable de decisión. Si una variable de decisión Xi debe cumplir condiciones de NO NEGATIVIDAD, debemos agregar la siguiente restricción: Xi 0

Programación Lineal Si la variable de decisión Xi puede asumir valores positivos o negativos se dice que Xi no tiene restricción de signo (SRS). En el ejemplo ambas variables de decisión se refieren a cantidades a producir, por lo tanto son no negativas. Sin embargo, en otros ejemplos las variables pueden ser SRS, por ejemplo en el caso de que Xi se refiere al saldo de alguna cuenta. Combinando todas las expresiones anteriores, es posible completar el modelo matemático para este problema de optimización, quedando de la siguiente forma:

Programación Lineal Definición de variables: X 1: número de mesas producidas por semana. X 2: número de sillas producidas por semana. F. O: Max Z = 3 X 1 + 2 X 2 S a: 2 X 1 + X 2 100 Horas disponibles para terminaciones por semana X 1 + X 2 80 Horas disponibles para carpintería por semana X 2 40 Producción máxima de sillas por semana Xj 0 j=1 y 2 No negatividad

Programación Lineal Generalización: Dado un conjunto de m desigualdades o ecuaciones lineales, con n variables, se requiere hallar valores de estas variables que satisfagan las restricciones y maximicen o minimicen alguna función lineal de las variables FO: Max o Min Z = C X Sujeto a AX B Xj 0 ; j = 1, 2, . . , n

Programación Lineal Matemáticamente Hallar Xj ; j = 1, 2, . . . , n Para Max o Min Z = C 1 X 1 + C 2 X 2 +. . . + Cn Xn Sujeto a a 11 X 1 +. . . + a 1 j Xj +. . . + a 1 n Xn ó b 1. . . ai 1 X 1 +. . . + aij Xj +. . . + ain Xn ó bi. . . am 1 X 1 +. . . + amj Xj +. . . + amn Xn ó bm Xj 0 j = 1, 2, . . . , n

Características de la PL 1. - Una función f(X 1, X 2, . . . , Xn) de X 1, X 2, . . . , Xn es una función lineal sí y sólo sí para un conjunto de constante C 1, C 2, . . . , Cn se tiene: f(X 1, X 2, . . . , Xn) = C 1 X 1 + C 2 X 2 +. . . + Cn. Xn Linealidad asume que no pueden haber términos del siguiente tipo: 2. - Asume las propiedades aditivas y multiplicativas • Si una unidad tipo 1 necesita 2 horas en la máquina A y una unidad tipo 2 necesita 3 horas, entonces ambas necesitan 5 horas. • Si una unidad tipo 3 necesita 1 hora en la máquina B, entonces 5 unidades necesitan 5 horas

Características de la PL 3. - La función que se va a optimizar se llama Función Objetivo y en ella no aparece ningún término independiente o constante. Los valores de las Xj son independientes de cualquier constante 4. - Los valores de las variables de decisión deben satisfacer un conjunto de restricciones. Cada restricción debe ser una ecuación o desigualdad lineal. 5. - Existe una restricción de signo asociada a cada variable. Para toda variable Xi la restricción de signo especifica si Xi debe ser no negativa o bien sin restricción de signo. 6. - En las m restricciones no deben considerarse las condiciones de no negatividad de las variables (Xj 0)

Características de la PL 7. - Supuesto de Divisibilidad, requiere que cada variable puede tomar valores fraccionarios. En el ejemplo anterior, el supuesto se traduce en que es aceptable producir 2, 4 sillas o 1, 6 mesas. Evidentemente este supuesto no es válido en el ejemplo, en este caso se puede proceder a formular el problema como un problema de programación lineal entera (PPE), problema en que una o más variables deben ser enteras. Cuando no se satisface el supuesto de divisibilidad, una posibilidad es redondear la solución obtenida a un valor entero, sin embargo, no existe garantías que dicha solución sea la mejor. 8. - Supuesto de Certeza: exige que cada parámetro, es decir, coeficientes de la función objetivo, coeficientes del lado derecho de las restricciones, etc. sean conocidos con certeza, es decir, no se acepta incertidumbre en sus valores

Características de la PL Regiones Factibles y Soluciones Óptimas Dos de los conceptos más fundamentales en los PPL son el de región factible y de solución óptima de un problema. Llamaremos punto a la especificación de un valor para cada variable de decisión. La región factible para un PPL es el conjunto de puntos que satisfacen todas las restricciones (incluidas las de signo) del problema. En el caso de un problema de maximización, una solución óptima del PPL es un punto de la región factible que está asociado al mayor valor posible de la función objetivo. Similarmente, para un problema de minimización, una solución óptima es un punto que está asociado al menor valor.

Características de la PL Cualquier conjunto Xj que satisface las restricciones se llama “solución al problema”. Si satisface la condición de no negatividad se llama “solución factible” y si además optimiza la función objetivo se llama “solución factible óptima” Usualmente hay un número infinito de soluciones factibles al problema, de todas estas se tiene que tratar de hallar, en lo posible, una óptima.