Toke pravci i ravnine Gordana Beissmann prof Sadraj

Točke, pravci i ravnine Gordana Beissmann, prof.

Sadržaj n n n n Aksiomi geometrije prostora Položaj pravaca u ravnini Položaj pravca i ravnine u prostoru Položaj pravaca u prostoru Određenost ravnine Položaj dviju ravnina u prostoru Položaj triju ravnina u prostoru 2

n n U izgradnji matematičkog opisa svijeta postoje pojmovi koji se ne mogu definirati pomoću jednostavnijih – njih smatramo poznatima samima po sebi. Umjesto pokušaja njihova definiranja dovoljno je popisati njihova osnovna svojstva aksiomima jer o tim pojmovima i njihovim osnovnim svojstvima postoji jasan geometrijski zor. 3

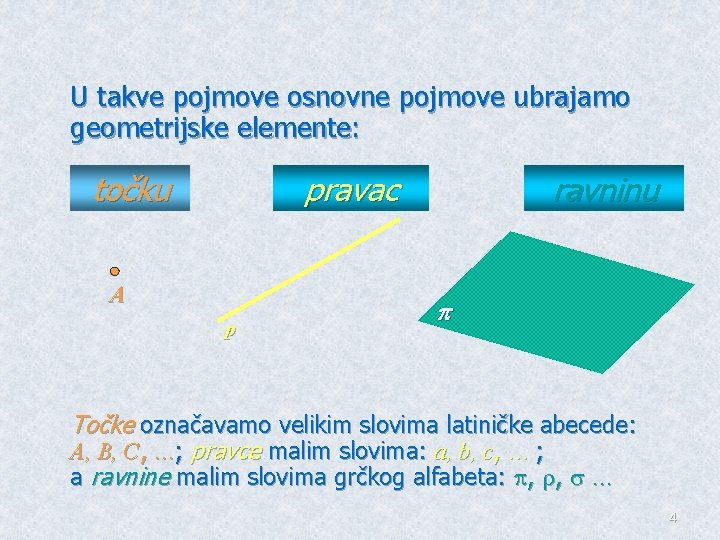
U takve pojmove osnovne pojmove ubrajamo geometrijske elemente: točku pravac A p ravninu Točke označavamo velikim slovima latiničke abecede: A, B, C, …; pravce malim slovima: a, b, c, … ; a ravnine malim slovima grčkog alfabeta: , , … 4

Aksiomi n n Najjednostavnija, elementarna svojstva koja se sama ne mogu dokazati, već se počevši od njih izvode sva ostala, nazivamo aksiomima. Aksiomi su tvrdnje koje se ne dokazuju, već se u okviru neke teorije drže ispravnima. 5

Aksiomi geometrije prostora A 1) Kroz dvije različite točke prolazi točno jedan pravac. p B A AB = p 6

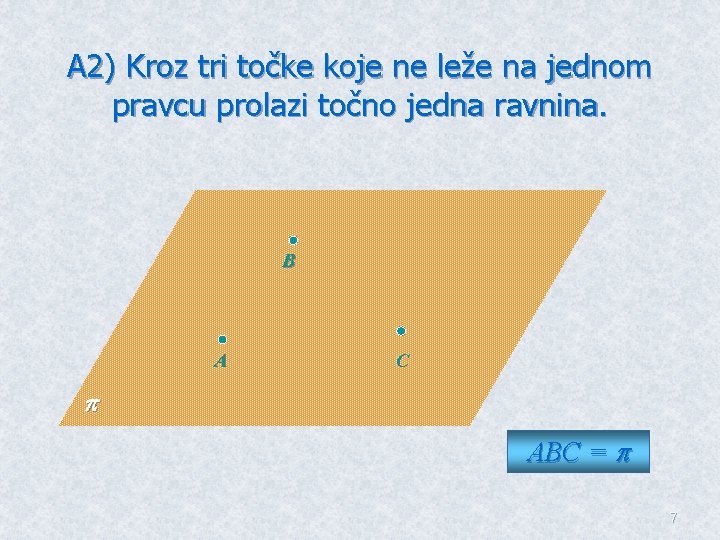
A 2) Kroz tri točke koje ne leže na jednom pravcu prolazi točno jedna ravnina. B A C ABC = 7

A 3) Pravac koji prolazi kroz dvije različite točke ravnine leži u toj ravnini. p A B p 8

A 4) Ako dvije različite ravnine imaju zajedničku točku, onda se sijeku po pravcu. p A =p 9

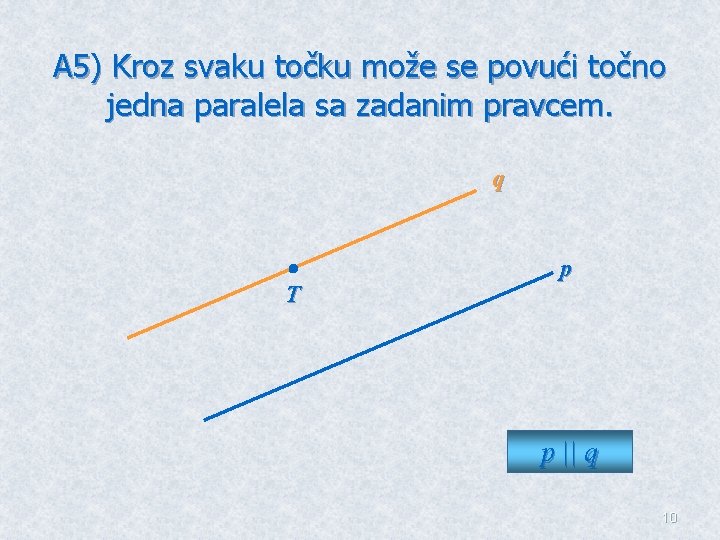
A 5) Kroz svaku točku može se povući točno jedna paralela sa zadanim pravcem. q T p p || q 10

Osnovni aksiomi geometrije prostora glase: (A 1) Kroz dvije različite točke prolazi točno jedan pravac. (A 2) Kroz tri točke koje ne leže na jednom pravcu prolazi točno jedna ravnina. (A 3) Pravac koji prolazi kroz dvije različite točke ravnine leži u toj ravnini. (A 4) Ako dvije različite ravnine imaju zajedničku točku, onda se sijeku po pravcu. (A 5) Kroz svaku točku može se povući točno jedna paralela sa zadanim pravcem. 11

Zadatak: Koristeći aksiome geometrije prostora odgovori na postavljena pitanja. Ako se dva pravca sijeku u dvije točke, tada su oni: 1. a) b) c) d) paralelni okomiti podudaraju se ništa od navedenog nije točno. Dvije ravnine prostora mogu se sjeći: 2. a) b) c) d) u jednoj točki u dvije točke po pravcu ne moraju se sjeći. 12

3. Je li neka od sljedećih dviju tvrdnji istinita: a) b) Kroz zadanu točku A i bio koju točku zadanog pravca p može se postaviti samo jedan pravac. Neka je H sjecište visina trokuta ABC. Kroz točke A i H može se postaviti samo jedan pravac. 13

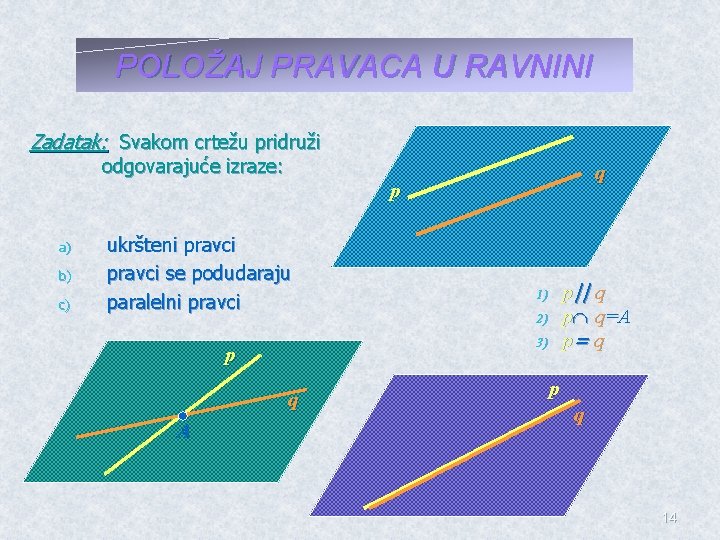
POLOŽAJ PRAVACA U RAVNINI Zadatak: Svakom crtežu pridruži odgovarajuće izraze: q p a) b) c) ukršteni pravci se podudaraju paralelni pravci 2) 3) p q A p|| q p q=A p= q 1) p q 14

Definicija: Za dva pravca p i q koja leže u istoj ravnini kažemo da su paralelni pravci ako se podudaraju ili se ne sijeku (pišemo: p||q). Zaključak: Dva su pravca u ravnini ili paralelna ili se sijeku u jednoj točki. Pritom paralelnost uključuje i slučaj istovjetnih pravaca. 15

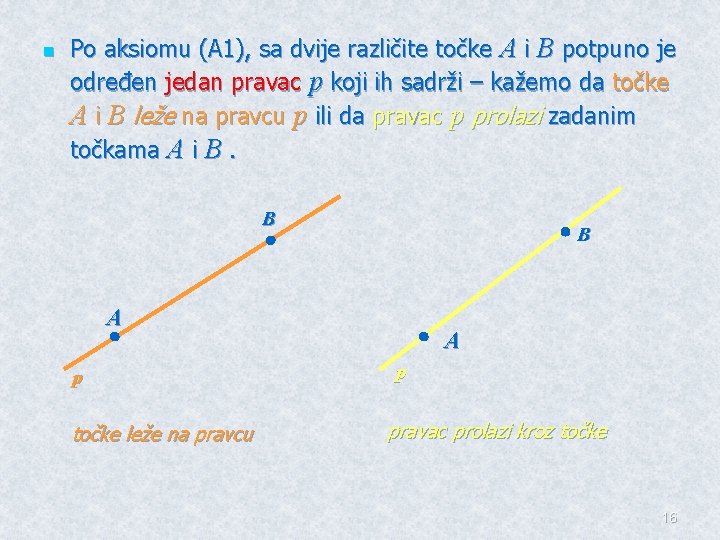
n Po aksiomu (A 1), sa dvije različite točke A i B potpuno je određen jedan pravac p koji ih sadrži – kažemo da točke A i B leže na pravcu p ili da pravac p prolazi zadanim točkama A i B. B B A p točke leže na pravcu A p pravac prolazi kroz točke 16

Definicija: Tri točke (ili više točaka) su kolinearne ako leže na istom pravcu. Tri točke (ili više točaka) su nekolinearne ako ne postoji pravac koji ih sadrži. B p A B A C C kolinearne točke nekolinearne točke 17

POLOŽAJ PRAVCA I RAVNINE U PROSTORU Pravac p i ravnina mogu se u prostoru nalaziti u tri različita položaja: 1. pravac leži u ravnini p p 18

2. pravac i ravnina se sijeku, pri čemu pravac ne leži u ravnini ( p = A ) p A p =A - točka A naziva se sjecište ili probodište pravca i ravnine 19

3. pravac i ravnina nemaju zajedničkih točaka (p|| ) - kažemo da je pravac p paralelan s ravninom p p || 20

Zaključak: Pravac i ravnina u prostoru ili su paralelni ili se sijeku u jednoj točki. Pritom paralelnost uključuje i slučaj kad pravac leži u ravnini. 21

Zadaci: 1. 2. U koliko točaka se sijeku pravac i ravnina u svakom od navedena tri slučaja? Zadana je ravnina i paralelogram ABCD. Može li ovoj ravnini pripadati: n n n točno jedan vrh paralelograma; točno dva vrha; točno tri vrha paralelograma? 22

POLOŽAJ PRAVACA U PROSTORU Dva pravca u prostoru mogu biti u jednom od sljedeća dva položaja: 1. 2. pravci leže u istoj ravnini, pravci ne leže u istoj ravnini. 23

1. pravci leže u istoj ravnini Definicija: Dva su pravca paralelna ako leže u istoj ravnini i ne sijeku se. q p p q 24

2. pravci ne leže u istoj ravnini Definicija: q Dva su pravca mimoilazna ako ne leže u istoj ravnini. p Korisno je poznavati jednostavan kriterij mimoilaznosti, koji kaže: ako jedan pravac leži u ravnini, a drugi pravac probada tu ravninu u točki koja ne pripada tom pravcu, onda su ta dva pravca mimoilazna. 25

Zaključak: Dva pravca u prostoru mogu biti u jednom od dva položaja: 1. 2. Pravci leže u istoj ravnini. Pravci su mimoilazni. 26

Zadaci: 1. 2. 3. Ako su pravci a i b mimoilazni, te b i c mimoilazni, jesu li nužno i pravci a i c mimoilazni? Kakav može biti međusoban položaj dvaju pravaca od kojih svaki leži u jednoj od dviju paralelnih ravnina? D Zadan je tetraedar ABCD. Moraju li uvijek C pravci AB i CD biti mimoilazni? B A 27

ODREĐENOST RAVNINE Kažemo da je ravnina zadana ili određena nekim elementima (točkama, pravcima) ako ih ona sadrži i ako je to jedina ravnina s tim svojstvom. (Često kažemo: ravnina je jednoznačno određena zadanim elementima. ) 28

pravcem i točkom koja ne leži na njemu tri točke koje ne leže na istom pravcu Ravnina je jednoznačno određena s: dva pravca koja se sijeku dva paralelna pravca koji se ne podudaraju 29

Uočimo da u svakom od navedenih slučajeva možemo istaknuti barem tri nekolinearne točke koje prema aksiomu (A 2) onda jednoznačno određuju ravninu. 30

Definicija: Ako neke točke leže u istoj ravnini, za njih kažemo da su komplanarne točke. Ako ne postoji ravnina koja ih sadrži, onda kažemo da su zadane točke nekomplanarne. C C A B komplanarne točke A B nekomplanarne točke 31

Zadaci: 1. Koliko različitih ravnina možemo postaviti kroz: a) b) c) dvije različite točke, tri različite točke, četiri različite točke od kojih nikoje tri nisu kolinearne? 2. Odredi najveći broj točaka u prostoru koje su uvijek komplanarne. 3. Koliko je različitih ravnina određeno s pet točaka od kojih nikoje četiri nisu komplanarne? 32

POLOŽAJ DVIJU RAVNINA U PROSTORU Dvije ravnine se u prostoru mogu naći u jednom od sljedeća tri položaja: 1. 2. 3. ravnine se podudaraju, ravnine se sijeku, ravnine se ne sijeku. 33

U koliko točaka se sijeku ravnine u svakom od navedenih slučajeva? p 1 2 1 2 U koliko se najmanje točaka prema osnovnim aksiomima geometrije prostora moraju sjeći zadane ravnine da bi nastupio svaki od navedenih slučajeva? 1 2 34

Definicija: Za dvije ravnine i kažemo da su paralelne ravnine ako se podudaraju ili se ne sijeku (pišemo: || ). Zaključak: Dvije ravnine prostora mogu biti ili paralelne ili je njihov presjek pravac. Pritom paralelnost uključuje slučaj kad su ravnine istovjetne. 35

POLOŽAJ TRIJU RAVNINA U PROSTORU Tri različite ravnine u prostoru mogu biti u jednom od sljedećih položaja: 1. 2. 3. 4. 5. sve tri ravnine su paralelne, ravnine se sijeku duž jednog pravca, po dvije ravnine sijeku se u tri paralelna pravca, dvije ravnine su paralelne, a treća ih siječe duž dva paralelna pravca, ravnine se sijeku u jednoj točki. 36

Zadatak: 1. Dvije ravnine koje se sijeku presječene su trećom ravninom. Mogu li dobivena dva pravca biti paralelna? 37