Todays topics Java Recursion Upcoming Graphics Reading Great

Today’s topics Java Recursion Upcoming Graphics Reading Great Ideas, Chapter 4 (begin Chapter 5 for graphics) Comp. Sci 001 14. 1

Recursion v v Actually have been using it in everyday life Dictionary Example q v Use Clone Model to sort this out q v v Need dictionary to use a dictionary o Look up word o Definition may use words we don’t understand o Look up those words o Etc. Like using multiple dictionaries Recursion implies a self-referential process In computing we say a function invokes itself Comp. Sci 001 14. 2

Recursion v Recursion is a Divide and Conquer strategy q q v Factorial Example q q q v Decomposing problem 1. Base Case (halting case) 2. Recursive case (which must get us closer to solution) If we don’t have base case, infinite recursion o Very much like an infinite loop o (very bad!) Definition of N Factorial (domain is non-negative integers) o N! = N * (N-1)! o 0! = 1 Note we defined factorial (or !) in terms of ! Which part corresponds to the base case? In class demo… Comp. Sci 001 14. 3

Factorial Program public class Rec. Fact extends java. applet. Applet implements Action. Listener { Text. Field m. Instruct, m. Results; Int. Field g. N; Button b. Fact; public void init() { m. Instruct = new Text. Field(70); m. Instruct. set. Text( "Enter N, then press button for factorial"); g. N = new Int. Field(10); g. N. set. Label("N"); b. Fact = new Button("Factorial"); m. Results = new Text. Field(70); add(m. Instruct); add(g. N); add(b. Fact); add(m. Results); b. Fact. add. Action. Listener(this); } Comp. Sci 001 14. 4

Factorial Program. 2 public int if (n == { return } return n } fact(int n) { 0) 1; * fact(n - 1); public void action. Performed(Action. Event event) { int k; k = g. N. get. Int(); m. Results. set. Text(k + " factorial = " + fact(k)); } } Comp. Sci 001 14. 5

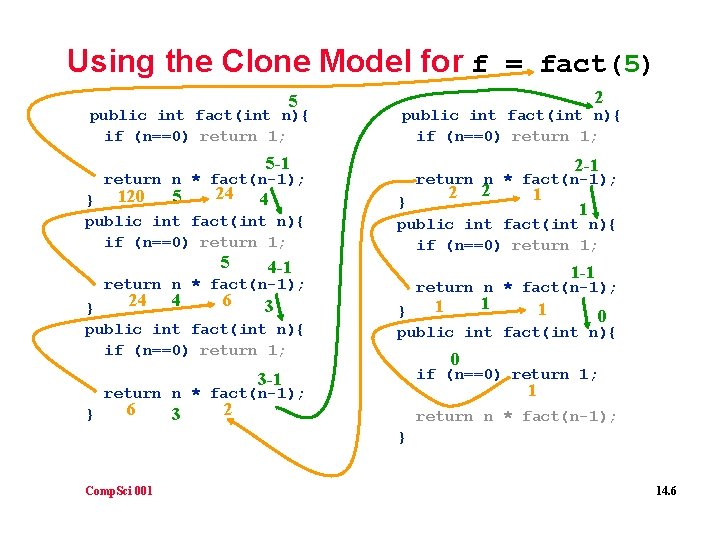
Using the Clone Model for f = fact(5) 5 public int fact(int n){ if (n==0) return 1; 2 public int fact(int n){ if (n==0) return 1; 5 -1 return n * fact(n-1); 24 4 5 } 120 public int fact(int n){ if (n==0) return 1; 5 2 -1 return n * fact(n-1); 2 4 -1 return n * fact(n-1); 24 4 6 3 } public int fact(int n){ if (n==0) return 1; 1 -1 return n * fact(n-1); 1 1 1 } 0 public int fact(int n){ 0 if (n==0) return 1; 3 -1 1 return n * fact(n-1); } 6 3 2 1 } 1 public int fact(int n){ if (n==0) return 1; 2 return n * fact(n-1); } Comp. Sci 001 14. 6

Recursive vs Iterative v Notice that recursive solution required No Loop q Repetition is implicit in the process v Could have used iterative public int fact(int n) { int prod = 1; while(n > 0) { prod = prod * n; n = n - 1; } return prod; (looping) approach: } v Is actually simpler for this problem q v For some problems, recursion is much easier (when comfortable with it) Watch the SIZE OF THE NUMBERS ! ! Comp. Sci 001 14. 7

Exponentiation v Want to calculate X to the Nth power q v Brute force approach q q v Also written as XN XN = X*X*X* … X*X How many multiplications? Can we do better? How would you calculate 7 64 with simple 4 -function calculator? Might calculate 49=7*7. Then can use 4932 q q How many multiplications now? Carry on with this idea: 2401 = 49*49. o Leaves us with 240116 Comp. Sci 001 14. 8

Exponentiation Recursively v Want to calculate X to the Nth power recursively v Base case: N = 0 X 0 = 1. 0 v Recursive case: N is an even number XN = XN/2 * XN/2 v Recursive case: N is an odd number XN = X * XN/2 v Ready to put this into code Comp. Sci 001 14. 9

Recursive Expon public class Recurse extends java. applet. Applet implements Action. Listener { Int. Field g. N; Double. Field g. X; Label l. N, l. X; Button b. Fact, b. Exp; Text. Field m. Results; int k, n; double x; public void init() { l. N = new Label("N"); l. X = new Label("X"); m. Instruct = new Text. Field(60); m. Instruct. set. Text( "Enter N and X, then press button for function"); Comp. Sci 001 14. 10

Recursive Expon. 2 g. N = new Int. Field(10); g. X = new Double. Field(10); b. Fact = new Button("Factorial"); b. Exp = new Button("Exponential"); m. Results = new Text. Field(60); b. Fact. add. Action. Listener(this); b. Exp. add. Action. Listener(this); add(m. Instruct); add(l. N); add(g. N); add(l. X); add(g. X); add(b. Fact); add(b. Exp); add(m. Results); } public void action. Performed(Action. Event event) { Object cause = event. get. Source(); if (cause == b. Fact) { n = g. N. get. Int(); x = g. X. get. Double(); m. Results. set. Text(n + " factorial = " + fact(n)); } Comp. Sci 001 14. 11

Recursive Expon. 3 if (cause == b. Exp) { n = g. N. get. Int(); x = g. X. get. Double(); m. Results. set. Text( x + " to the " + n + " power = " + expon(x, n)); } } int fact(int n) { if (n<=1) { return 1; } return n * fact(n-1); } Comp. Sci 001 14. 12

Recursive Expon. 4 double expon(double x, int n) { double xnot; if (n == 0) { return 1. 0; } xnot = expon(x, n/2); if ( n == 2*(n/2)) { // or if (n%2 == 0) i. e. , is it even? return xnot * xnot; } else { return x * xnot; } } } Comp. Sci 001 14. 13

Other uses of Recursion v Recursion sometime associated with self-similar structure q q v Processing folders (directories) q q v Important in computer science (think of your family tree) Many other applications Recursion can be expensive q q v Each folder may contain files or other folders Folder containing folders is self-referential Processing tree-like data structures q v Fractals are a graphic instantiation of similar ideas Will look at this later Each invocation of a method (function) incurs overhead Use iteration when this is obvious solution (e. g. N!) For many complicated problems, recursive solution is easier! Comp. Sci 001 14. 14

Church-Markov-Turing Thesis Any non-trivial computer language that one can invent is apparently capable of computing no more and no fewer functions than all other nontrivial programming languages. This part of Java lets you solve all kinds of problems and implement all computer algorithms. See how far we have gotten! Comp. Sci 001 14. 15