Todays Lesson Comparing Linear Quadratic Exponential Functions DECEMBER

Today’s Lesson: Comparing Linear, Quadratic, & Exponential Functions DECEMBER, 14, 2017

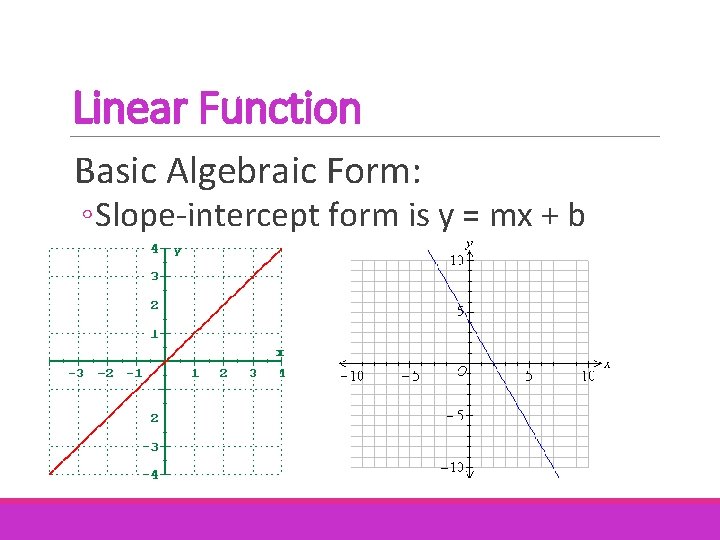
Linear Function Basic Algebraic Form: ◦ Slope-intercept form is y = mx + b

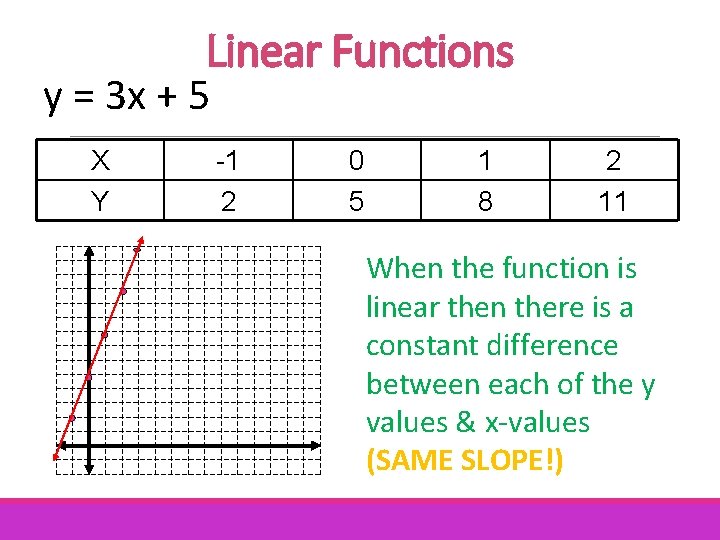
Linear Functions y = 3 x + 5 X Y -1 2 0 5 1 8 2 11 When the function is linear then there is a constant difference between each of the y values & x-values (SAME SLOPE!)

Word Problem - Linear ABC bowling charges $5 for shoe rental and then an additional $3 per game bowled. If Chelsie bowls 4 games, how much will she have to pay?

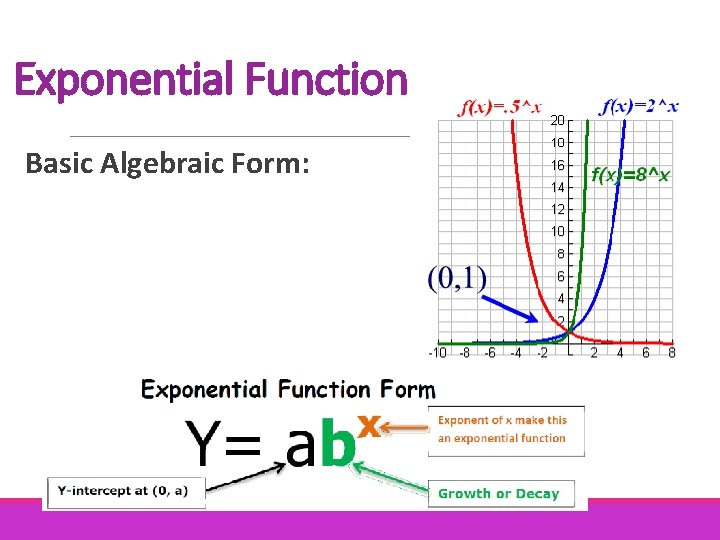
Exponential Function Basic Algebraic Form:

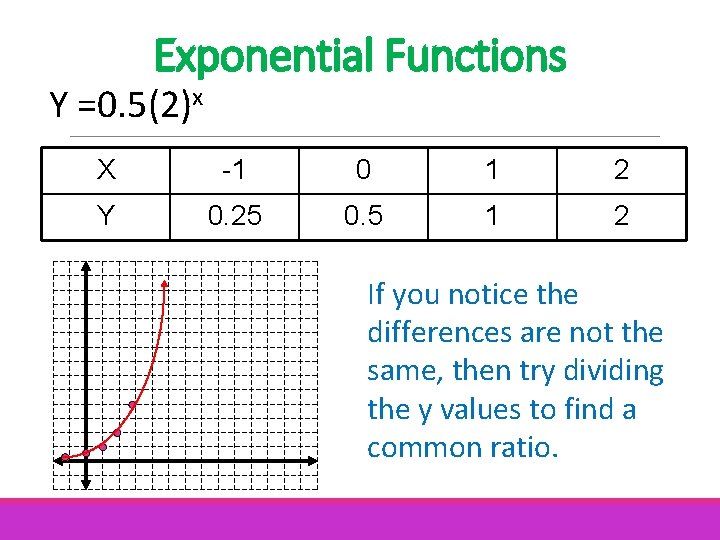
Exponential Functions Y =0. 5(2)x X -1 0 1 2 Y 0. 25 0. 5 1 2 If you notice the differences are not the same, then try dividing the y values to find a common ratio.

Word Problem – Exponential A colony of bacteria has a mass 0. 5 grams and doubles every hour. How much will the colony of bacteria weigh after 6 hours?

Quadratic Functions

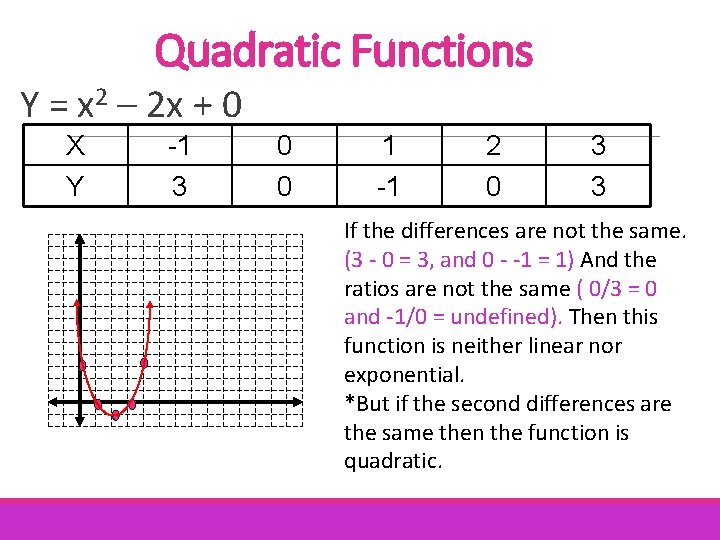
Quadratic Functions Y = x 2 – 2 x + 0 X Y -1 3 0 0 1 -1 2 0 3 3 If the differences are not the same. (3 - 0 = 3, and 0 - -1 = 1) And the ratios are not the same ( 0/3 = 0 and -1/0 = undefined). Then this function is neither linear nor exponential. *But if the second differences are the same then the function is quadratic.

Word Problem – Quadratic The product of a number and the number minus four is -3. What is the number?

Identifying from an equation: Linear Quadratic Exponential Has an x with no exponent. Has an x 2 in the equation. Has an x as the exponent. y = 5 x + 1 y = ½x 2 x + 3 y = 6 y= 2 x 2 y= x 2 + 3 x – 5 x 2 +9 + 4 y = 7 y = 3 x + 1 y = 52 x 4 x + y = 13

Examples: LINEAR, QUADRATIC or EXPONENTIAL? a)y = 6 x + 3 b)y = 7 x 2 +5 x – 2 c)9 x + 3 = y d)42 x = 8

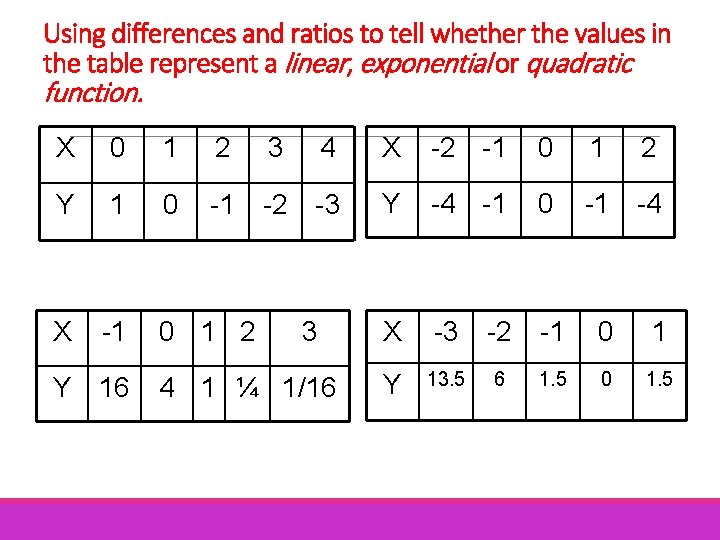
Using differences and ratios to tell whether the values in the table represent a linear, exponential or quadratic function. X 0 1 2 4 X -2 -1 0 1 Y 1 0 -1 -2 -3 Y -4 -1 0 -1 -4 X -1 X -3 -2 -1 0 1 Y 13. 5 6 1. 5 0 1. 5 Y 16 0 1 2 3 3 4 1 ¼ 1/16 2

A chambered nautilus is a marine animal that lives in the outermost chamber of its shell. When the Nautilus outgrows a chamber it adds a new, larger chamber to its shell. The table shows the volumes (in cubic cm) of consecutive chambers of a nautilus. Tell whether the data can be modeled by a linear function, an exponential function, or a quadratic function. Chamber Volume (cm 3) 1 2 3 4 5 6 0. 837 0. 889 0. 945 1. 005 1. 068 1. 135

The table shows the body temperature B (in degrees Celsius) of a desert spiny lizard at various air temperatures A (in degrees Celsius) Tell whether the data can be modeled by a linear function, an exponential function, or a quadratic function. Air Temp, A (ºC) 26 27 28 29 30 Body Tem (ºC) 33. 44 33. 78 34. 12 34. 46 34. 80

The time it takes for a clock’s pendulum to swing from one side to another and back again is called the pendulums period. The table shows the period t (in seconds) of a pendulum of length l (in feet). Tell whether the data can be modeled by a liner function, and exponential function or a quadratic function. Period, t(sec) 1 2 3 4 5 Length, l (ft) 0. 82 3. 28 7. 38 13. 12 20. 5

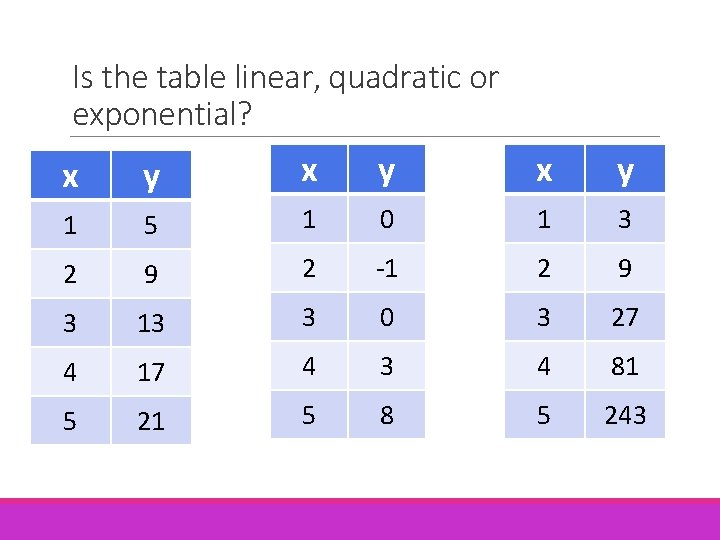
Is the table linear, quadratic or exponential? x y x y 1 5 1 0 1 3 2 9 2 -1 2 9 3 13 3 0 3 27 4 17 4 3 4 81 5 21 5 8 5 243

Homework COMPARING FUNCTIONS WORKSHEET