Todays Lecture Objectives Review Learn fluid dynamics Conservation

Today’s Lecture Objectives: – Review (Learn) fluid dynamics • Conservation equation – Mass – Momentum – Energy

Terminology • • Fluid particle Scalar vs. Vector Boundary conditions Steady State vs. Unsteady State Stream lines Gradient Lines Incompressible vs. Compressible fluids …… – Examples

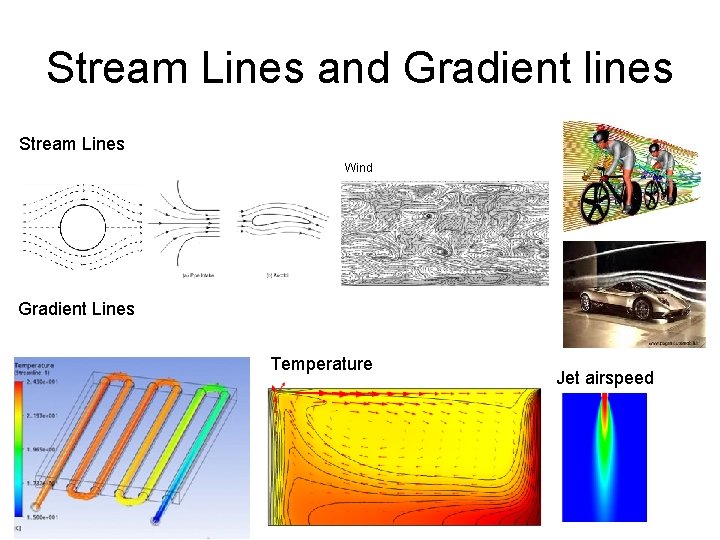
Stream Lines and Gradient lines Stream Lines Wind Gradient Lines Temperature Jet airspeed

Steady-state vs. Unsteady-stat https: //www. youtube. com/watch? v=IDe. GDFZSYo 8

Notations Velocity components: • • On the white board: vx, vy, vz In the book: u v w Time: , Time period: T Vector: V scalar: vx Density: Pressure: p, Concentration: C, … General notation for scalar (can be any , vx, …) Finite spatial distance(length): ∆x, ∆y, ∆z; Finite volume: V Infinitely small length: x, y, z ; Infinitely small volume: V Force F, Normalized force: f= F/V; Stress: xx, xy Mass: m, acceleration a Area: Ax, Ay, Az In this class we will primarily Cartesian coordinate system

Control Volumes 1) Volume is fixed in space (Eulerian type). Fluid can freely pass through the volume’s boundary. 2) 2)Volume is attached to the fluid (Lagrangian type). Volume is freely carried along with the fluid, and no fluid passes through its boundary.

Total Derivative Shows how variable change during time while traveling from A to B Change in are introduced by changing boundary conditions over time and by moving from part A to B z mathematical definition A y Total derivative allows all arguments vary x Physical interpretation … B V

Fluid Dynamics: Conservation equations

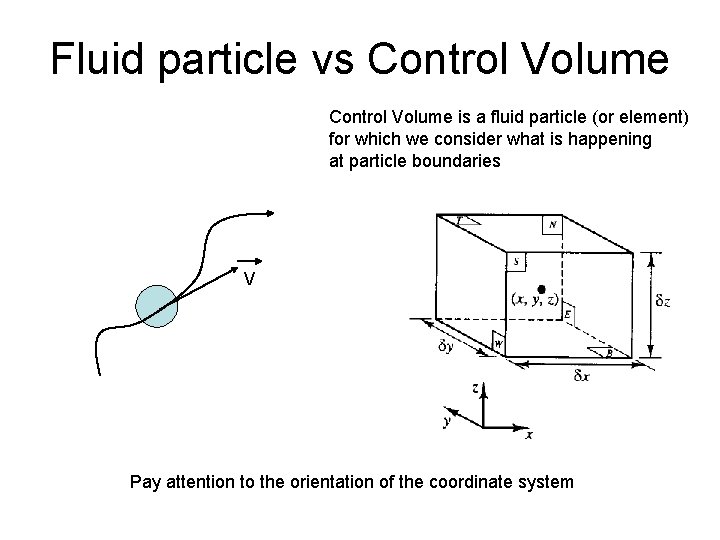
Fluid particle vs Control Volume is a fluid particle (or element) for which we consider what is happening at particle boundaries V Pay attention to the orientation of the coordinate system

Important operations Total derivative for fluid particle which is moving: V z any scalar y Vector and scalar operators: scalar vector x

Gradient of a scalar and Divergence of a vector Gradient of a scalar - nabla operator Divergence of a vector Vector filed You can also write that Where is the gradient of temperature largest?

Notation Density ( ) In our problems (indoor and outdoor air and water flows) the change of is so small that we can assume constant (most of the time) Incompressible flow vs. incompressible fluid ! Book (handouts) vs. Class notes We are going to use these interchangeably Vx ≡ u Vy ≡ v Vz ≡ w

Continuity equation -conservation of mass Mass flow in and out of control volume Infinitely small volume V = δxδyδz Volume sides: Ax = δyδz Ay = δxδz Az = δxδy Change of density in volume = = Σ(Mass in) - Σ(Mass out) same = …. ………………. See equation 2. 2 in notes

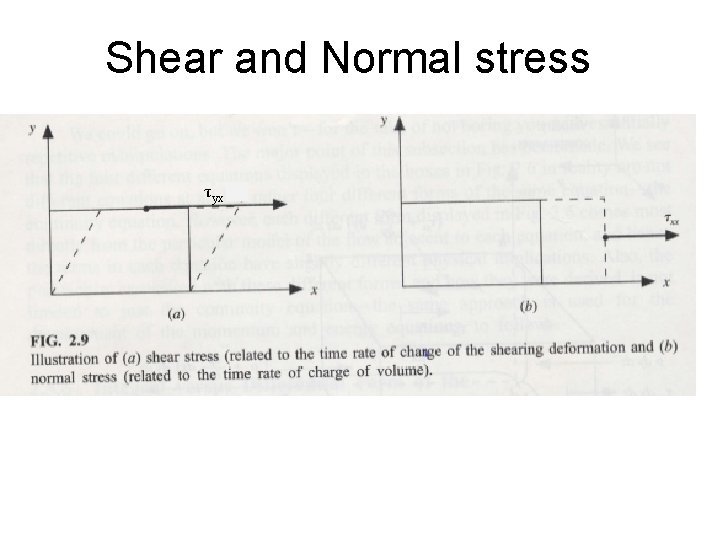
Shear and Normal stress τyx

Momentum equation –Newton’s second law dimensions of fluid particle Stress components in x direction total derivative forces per unit of volume in direction x ……………….

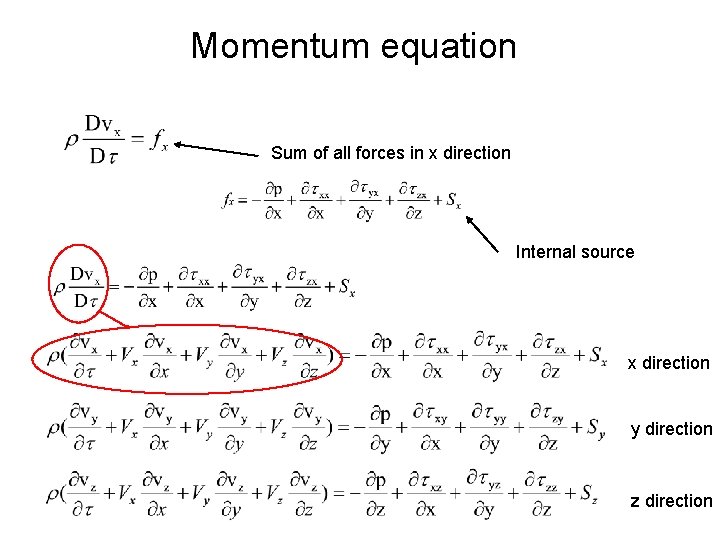
Momentum equation Sum of all forces in x direction Internal source x direction y direction z direction

Newtonian fluids • Viscous stress are proportional to the rate of deformation (e) Elongation: Shearing deformation: Viscous stress: viscosity For incompressible flow 0

Momentum equations for Newtonian fluids After substitution: x direction: y direction: z direction:

Momentum equations for Newtonian fluids Same like previous slide with some rearrangements: x direction: 0 y direction: z direction:

Momentum equations for Newtonian fluids Finally: x direction: y direction: z direction: