Today in Inorganic Uses of Symmetry in Chemistry

First, some housekeeping 1. What sections of Chapter 3 are we covering? (in Housecroft)

Symmetry may be defined as a feature of an object which is invariant to

Previously in Inorganic…. Today in Inorganic…. 1. Properties of Groups - Introduction to Inorganic

When all the Symmetry of an item are taken together, magical things happen. The

Let’s see how this works with symmetry operations. NOTE: that only symmetry operations form

Now, observe what the C 3 operation does: 1 3 C 3 2 1

A useful way to check the 4 group properties is to make a “multiplication”

Now, observe what happens when two different symmetry elements exist together: Start with an

Now, observe what happens when two symmetry elements exist together: Now add one mirror

Now, observe what happens when two symmetry elements exist together: 1 3 3 C

Here’s the thing: Do the set of operations, {E, C 32 s 1} still

This is the problem, right? How to get from A to C in ONE

What is needed? Another mirror plane! 1 3 3 C 3 2 2 s

And if there’s a 2 nd mirror, there must be …. 1 1 3

“Multiplication” Table for set of Symmetry Operations {E, C 32, s 1, s 2,

We answered this question: Does the set of operations {E, C 32 s 1

Inhuman Transformations (not a horror movie!) 5 types of symmetry operations. Which one(s) can

The set of symmetry operations that forms a Group is call a Point Group—it

What’s the difference between: sv and sh sv is parallel to major rotation axis,

Previously in Inorganic…. Today in Inorganic…. 1. Classes of Point Groups - Properties of

The Types of point groups If an object has no symmetry (only the identity

Linear Groups or cylindrical class C∞v and D∞h = C∞ + infinite sv =

See any repeating relationship among the Cubic groups ? T: 4 C 3 and

Slides: 45

Download presentation

Today in Inorganic…. Uses of Symmetry in Chemistry Symmetry elements and operations Properties of Groups Symmetry Groups, i. e. , Point Groups Learn how to see differently…. .

First, some housekeeping 1. What sections of Chapter 3 are we covering? (in Housecroft) In Chapter 3: 3. 1 -. 7 (to p. 76) and 3. 8 2. 1 st Problems set due next Thursday.

Symmetry may be defined as a feature of an object which is invariant to transformation Symmetry elements are geometrical items about which symmetry transformations—or symmetry operations—occur. There are 5 types of symmetry elements. 1. Mirror plane of reflection, s z y x

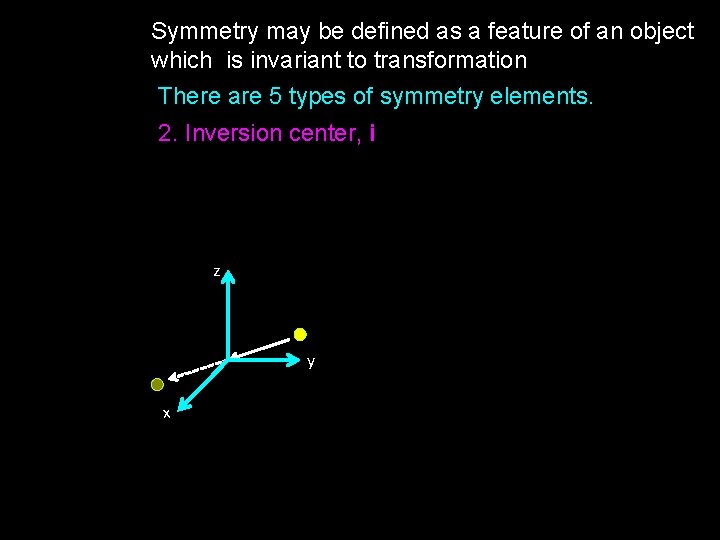
Symmetry may be defined as a feature of an object which is invariant to transformation There are 5 types of symmetry elements. 2. Inversion center, i z y x

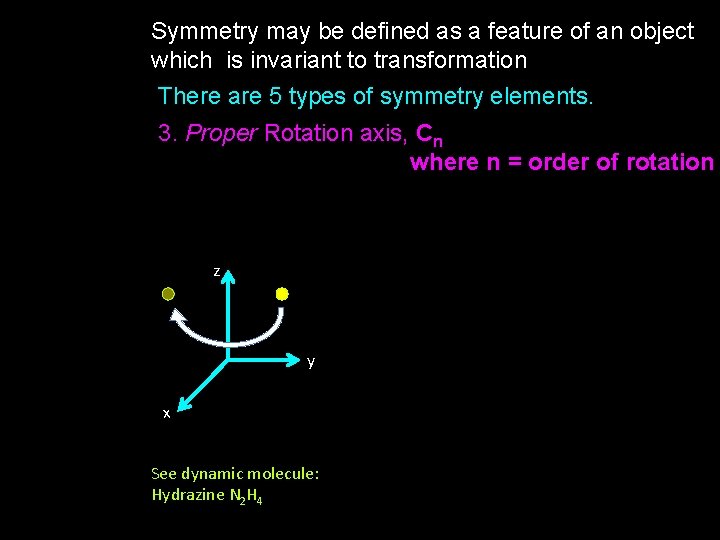
Symmetry may be defined as a feature of an object which is invariant to transformation There are 5 types of symmetry elements. 3. Proper Rotation axis, Cn where n = order of rotation z y x See dynamic molecule: Hydrazine N 2 H 4

Previously in Inorganic…. Today in Inorganic…. 1. Properties of Groups - Introduction to Inorganic - Uses of Symmetry in Chemistry - Symmetry elements and operations 2. Symmetry Groups, i. e. , Point Groups and How to Assign Point Groups “the flowchart” 3. Classes of Point Groups 4. Inhuman Transformations Learn how to see differently…. .

Symmetry may be defined as a feature of an object which is invariant to transformation There are 5 types of symmetry elements. 4. Improper Rotation axis, Sn where n = order of rotation Something NEW!!! Cn followed by s z y See dynamic molecule:

Symmetry may be defined as a feature of an object which is invariant to transformation There are 5 types of symmetry elements. 5. Identity, E, same as a C 1 axis z y x

When all the Symmetry of an item are taken together, magical things happen. The set of symmetry operations (NOT elements) in an object can form a Group A “group” is a mathematical construct that has four criteria (‘properties”) A Group is a set of things that: 1) has closure property 2) demonstrates associativity 3) possesses an identity 4) possesses an inversion for each operation

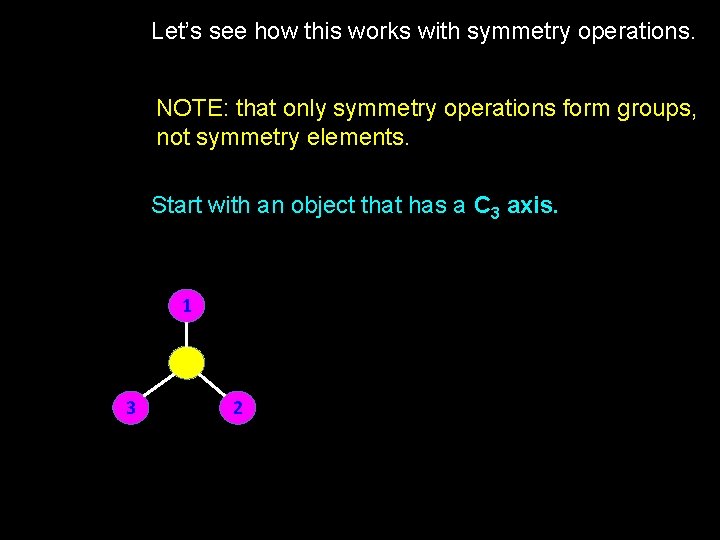
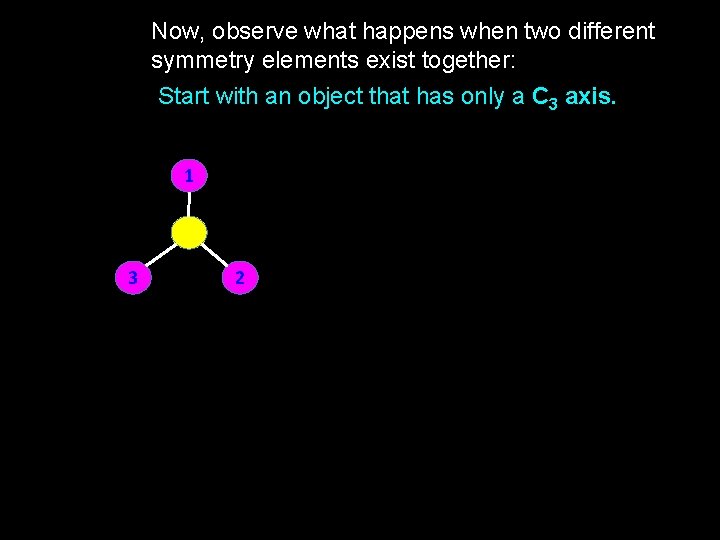
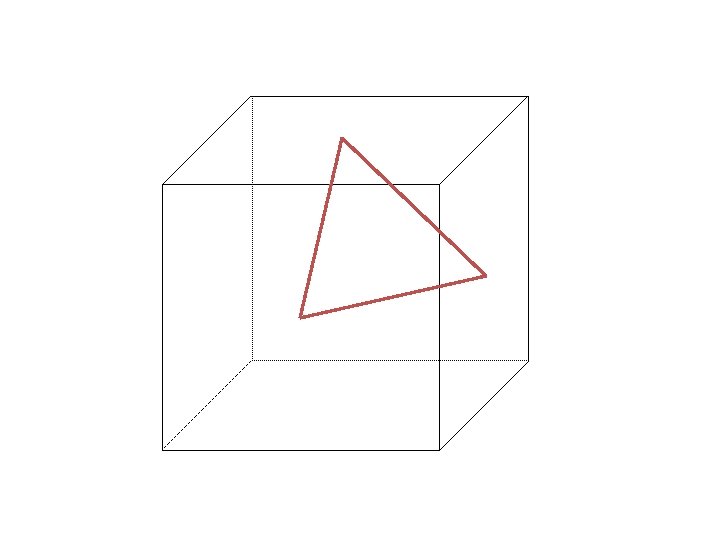
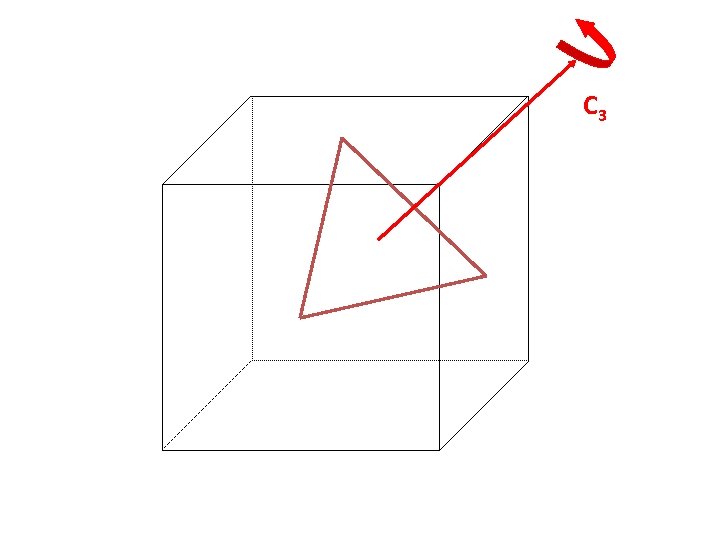
Let’s see how this works with symmetry operations. NOTE: that only symmetry operations form groups, not symmetry elements. Start with an object that has a C 3 axis. 1 3 2

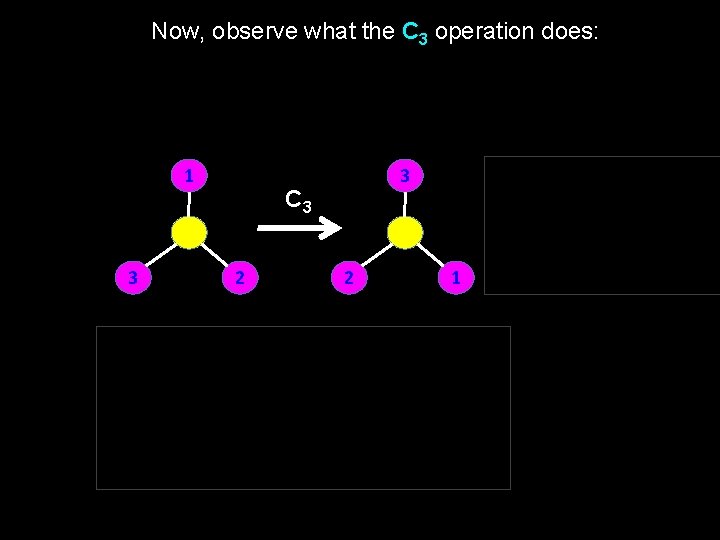
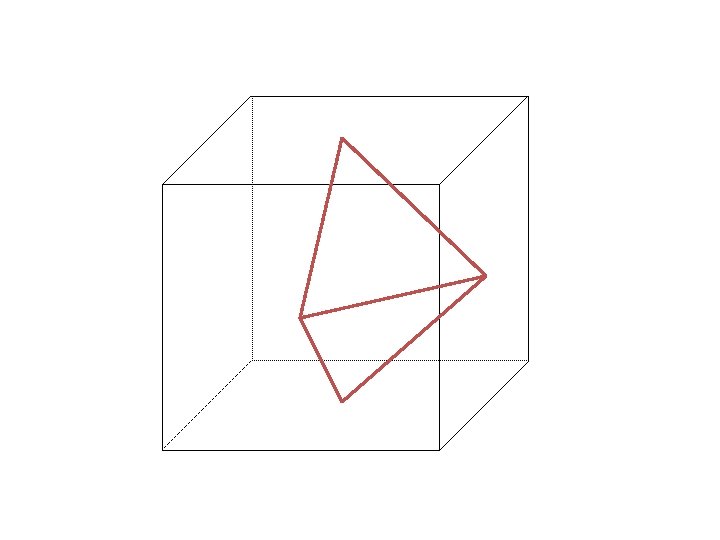
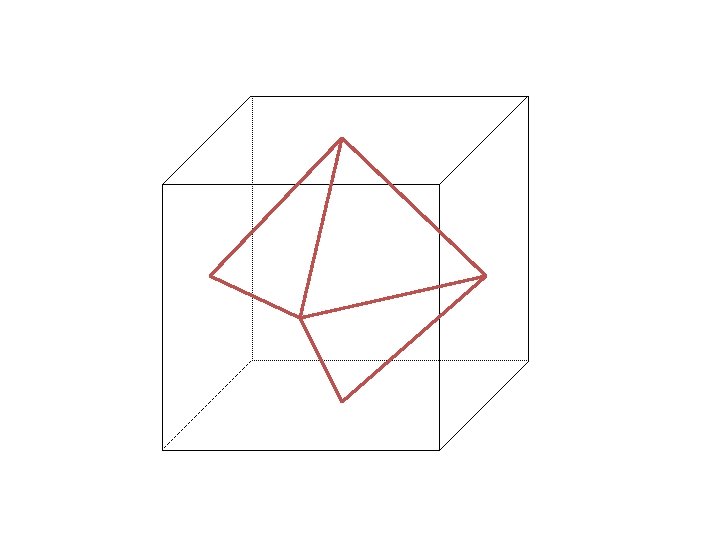
Now, observe what the C 3 operation does: 1 3 C 3 2 1 3 2 C 3 2 2 3 C 3 1 2 2 1 3

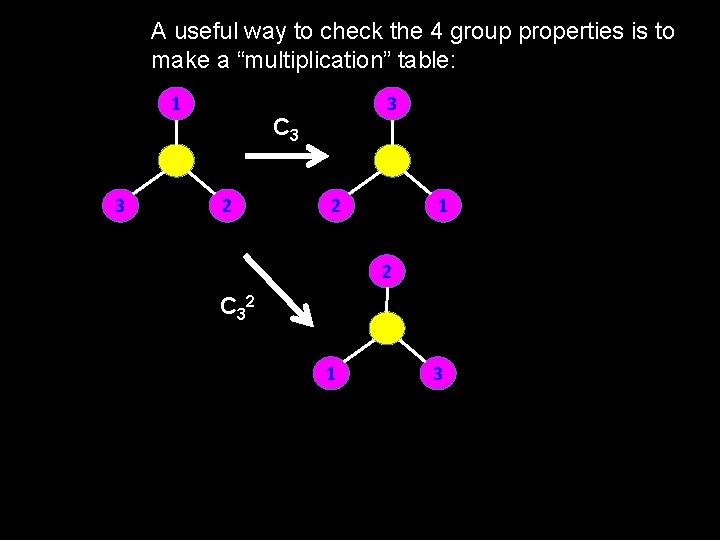
A useful way to check the 4 group properties is to make a “multiplication” table: 1 3 3 C 3 2 2 1 2 C 32 1 3

Now, observe what happens when two different symmetry elements exist together: Start with an object that has only a C 3 axis. 1 3 2

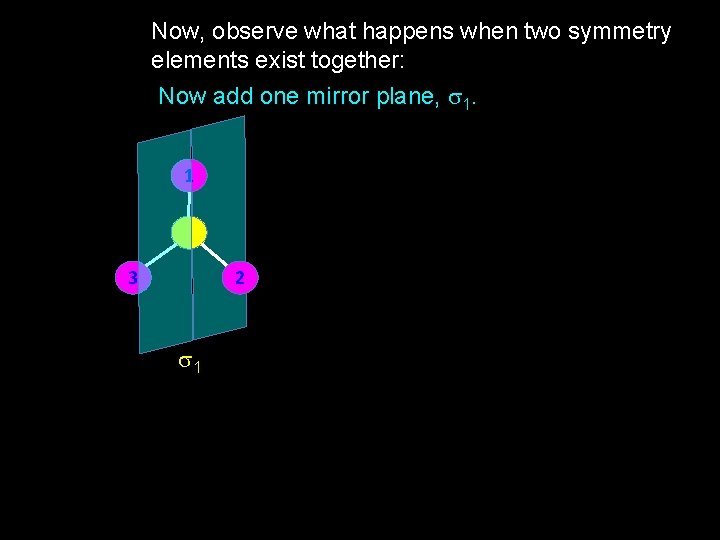
Now, observe what happens when two symmetry elements exist together: Now add one mirror plane, s 1. 1 3 2 s 1

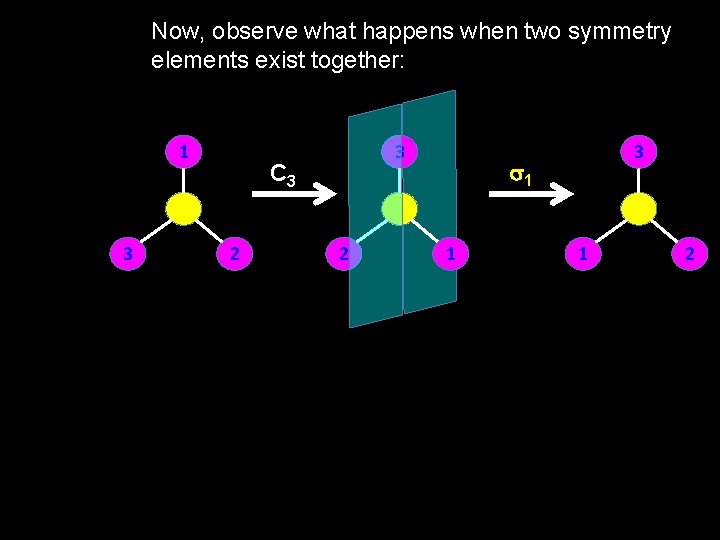
Now, observe what happens when two symmetry elements exist together: 1 3 3 C 3 2 2 3 s 1 1 1 2

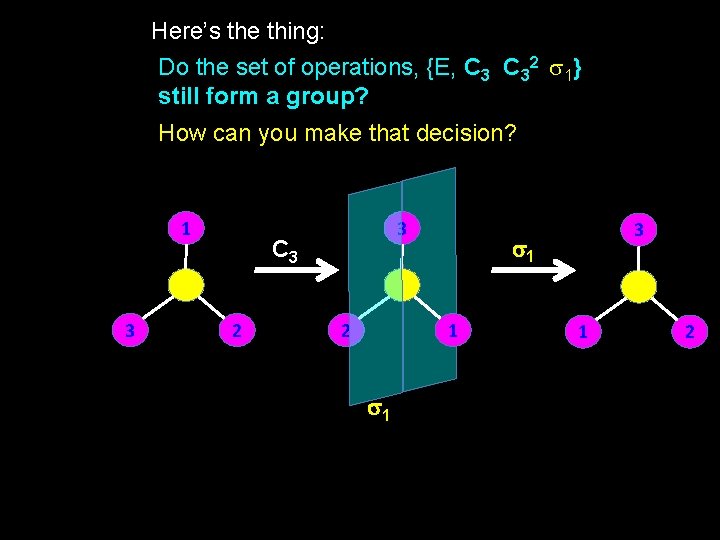
Here’s the thing: Do the set of operations, {E, C 32 s 1} still form a group? How can you make that decision? 1 3 3 C 3 2 2 s 1 1 s 1 3 1 2

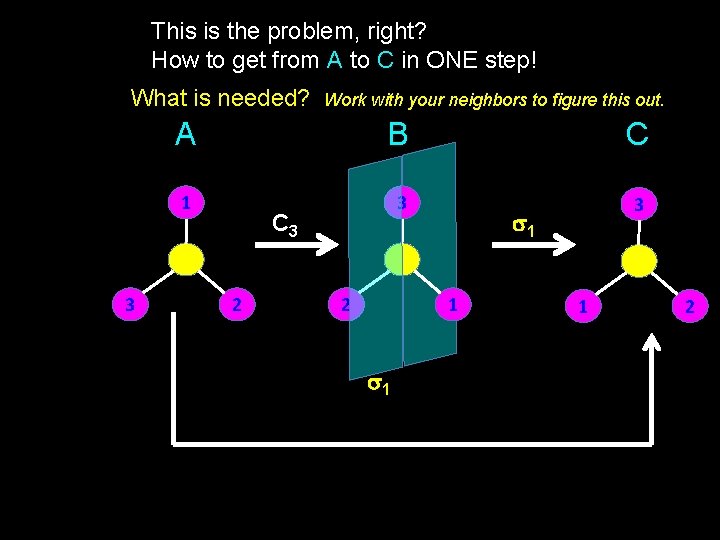
This is the problem, right? How to get from A to C in ONE step! What is needed? 3 Work with your neighbors to figure this out. A B C 1 3 3 C 3 2 2 s 1 1 2

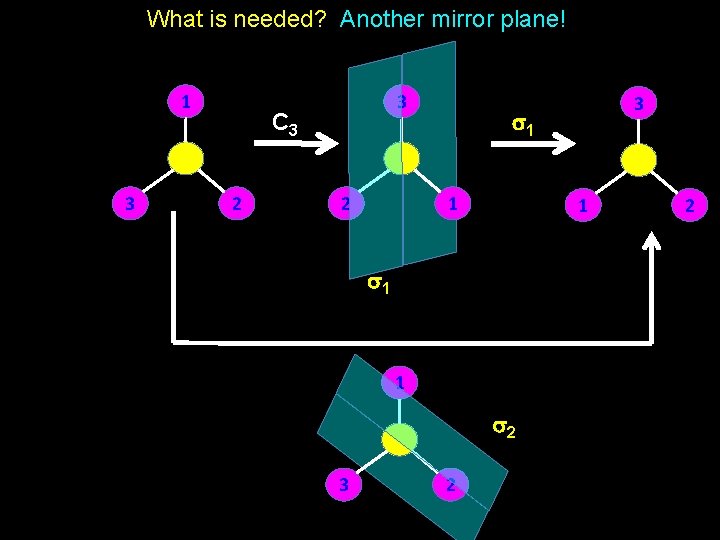
What is needed? Another mirror plane! 1 3 3 C 3 2 2 s 1 1 1 s 2 3 3 2 2

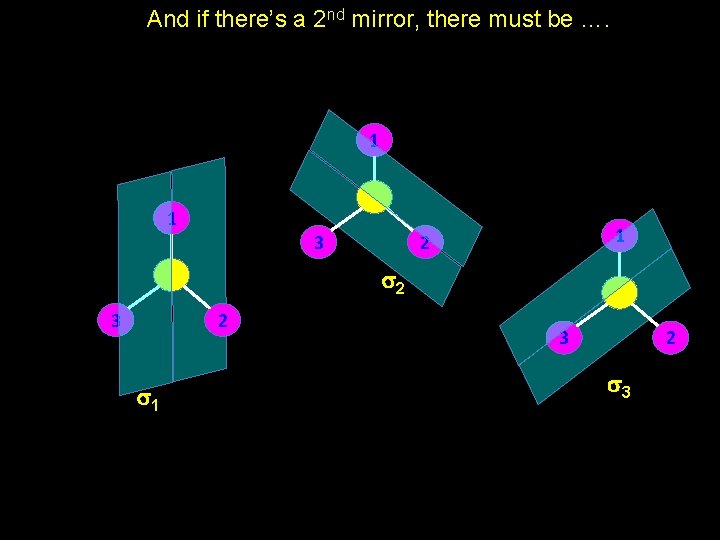
And if there’s a 2 nd mirror, there must be …. 1 1 3 1 2 s 2 3 2 s 1 3 2 s 3

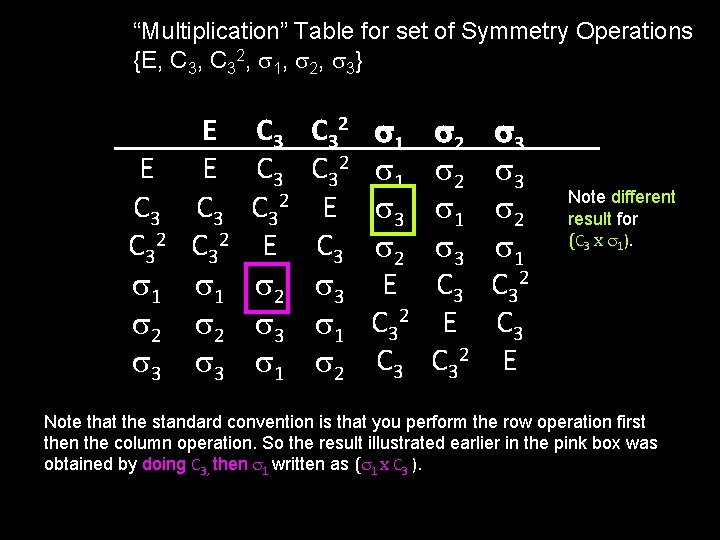
“Multiplication” Table for set of Symmetry Operations {E, C 32, s 1, s 2, s 3} E C 3 2 s 1 s 2 s 3 E E C 3 2 s 1 s 2 s 3 C 3 C 3 2 E s 2 s 3 s 1 C 3 2 E C 3 s 1 s 2 s 1 s 3 s 2 E C 3 2 C 3 s 2 s 1 s 3 C 3 E C 3 2 s 3 s 2 s 1 C 3 2 C 3 E Note different result for (C 3 x s 1). Note that the standard convention is that you perform the row operation first then the column operation. So the result illustrated earlier in the pink box was obtained by doing C 3, then s 1 written as (s 1 x C 3 ).

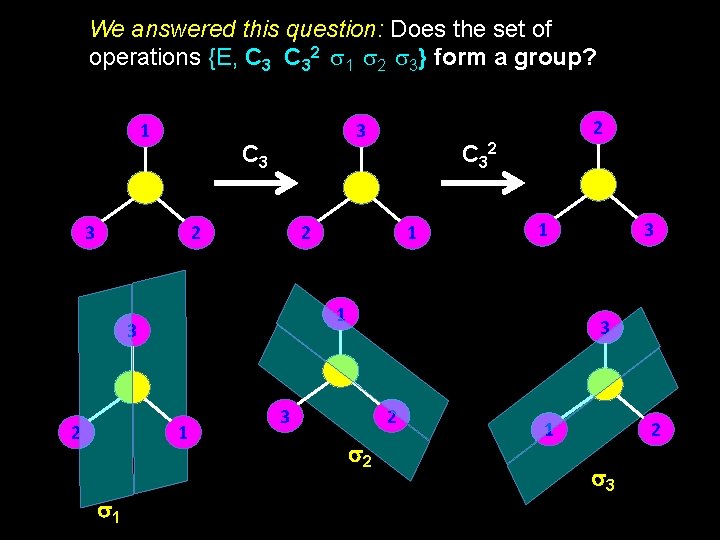
We answered this question: Does the set of operations {E, C 32 s 1 s 2 s 3} form a group? 1 C 3 3 2 1 1 s 1 C 32 2 3 3 3 3 2 s 2 1 2 s 3

Inhuman Transformations (not a horror movie!) 5 types of symmetry operations. Which one(s) can you do? ? Rotation Reflection Inversion Improper rotation Identity

The set of symmetry operations that forms a Group is call a Point Group—it describes completely the symmetry of an object around a point. The set {E, C 32 s 1 s 2 s 3} includes the operations of the C 3 v point group. Point Group symmetry assignments for any object can most easily be assigned by following a flowchart.

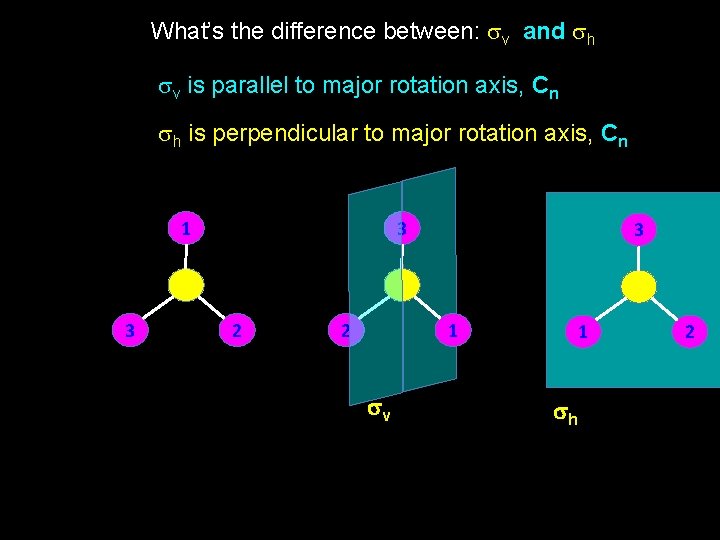
What’s the difference between: sv and sh sv is parallel to major rotation axis, Cn sh is perpendicular to major rotation axis, Cn 1 3 3 2 2 3 1 sv 1 sh 2

Previously in Inorganic…. Today in Inorganic…. 1. Classes of Point Groups - Properties of Groups 2. Symmetry and Chirality - How to Assign Point Groups - Inhuman Transformations Learn how to see differently…. . 3. Intorduction Character Tables

The Types of point groups If an object has no symmetry (only the identity E) it belongs to group C 1 Axial Point groups or Cn class Cn = E + n Cn ( n operations) Cnh= E + n Cn + sh (2 n operations) Cnv = E + n Cn + n sv ( 2 n operations) Dihedral Point Groups or Dn class Dn = Cn + n. C 2 (^) Dnd = Cn + n. C 2 (^) + n sd Dnh = Cn + n. C 2 (^) + sh Sn groups: S 1 = Cs S 2 = Ci S 3 = C 3 h S 4 , S 6 forms a group S 5 = C 5 h

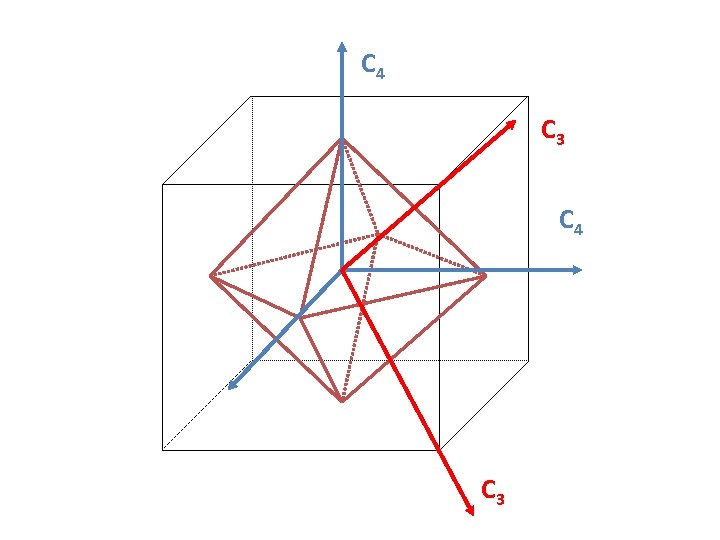
Linear Groups or cylindrical class C∞v and D∞h = C∞ + infinite sv = D∞ + infinite sh Cubic groups or the Platonic solids. . T: 4 C 3 and 3 C 2, mutually perpendicular Td (tetrahedral group): T + 3 S 4 axes + 6 sv O: 3 C 4 and 4 C 3, many C 2 Oh (octahedral group): O + i + 3 sh + 6 sv Icosahedral group: Ih : 6 C 5, 10 C 3, 15 C 2, i, 15 sv

See any repeating relationship among the Cubic groups ? T: 4 C 3 and 3 C 2, mutually perpendicular Td (tetrahedral group): T + 3 S 4 axes + 6 sv O: 3 C 4 and 4 C 3, many C 2 Oh (octahedral group): O + i + 3 sh + 6 sv Icosahedral group: Ih : 6 C 5, 10 C 3, 15 C 2, i, 15 sv

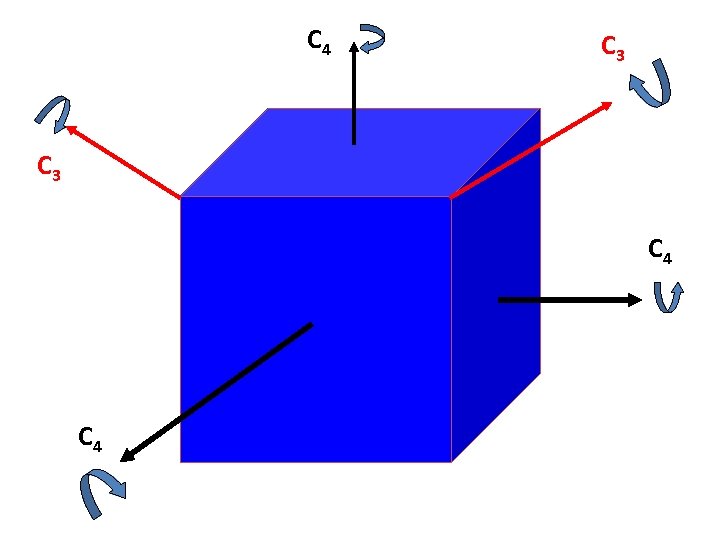
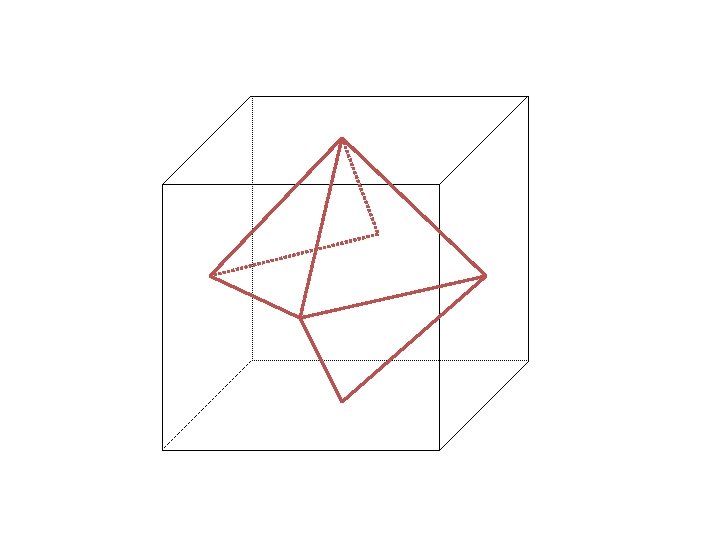
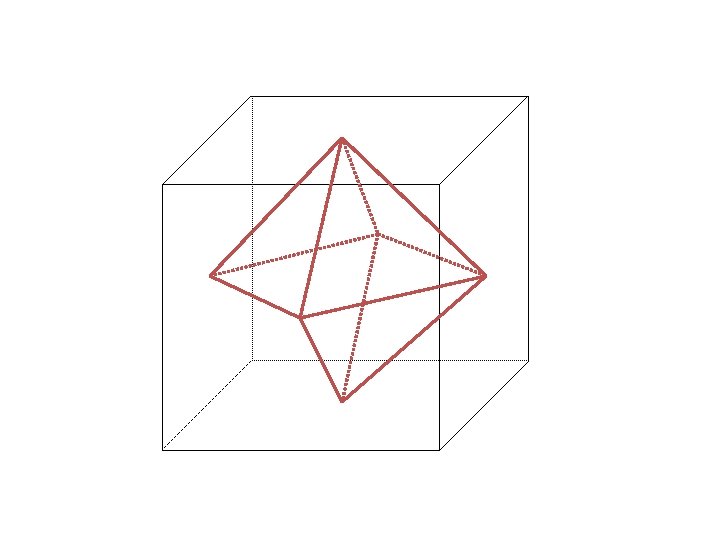
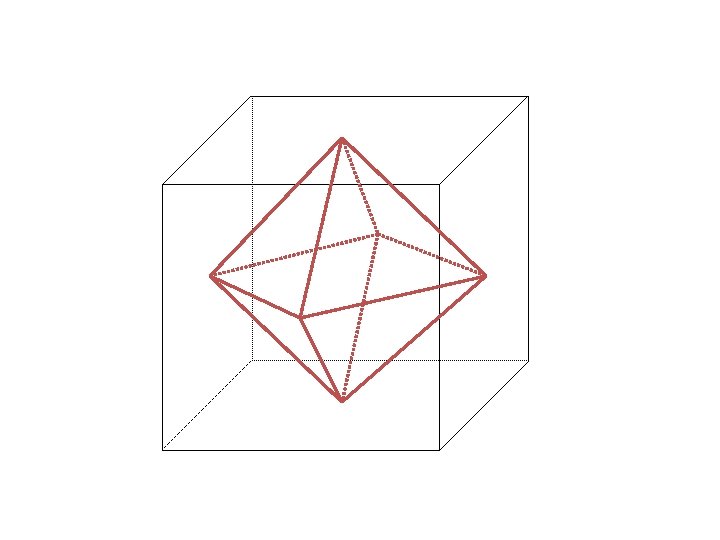
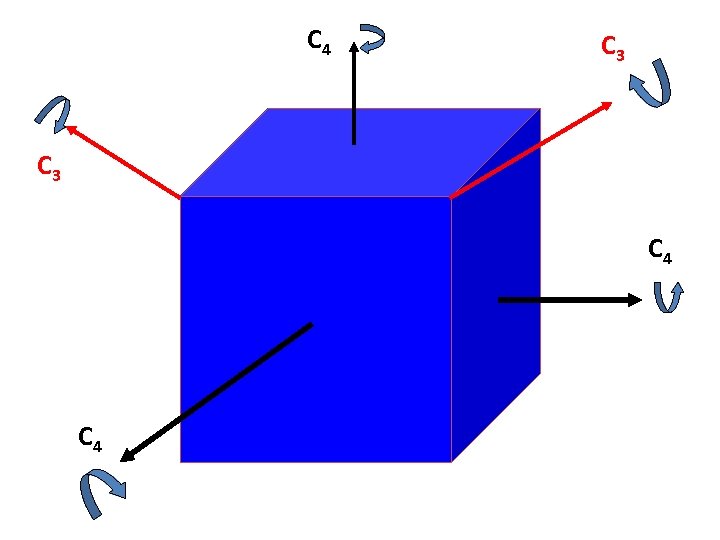
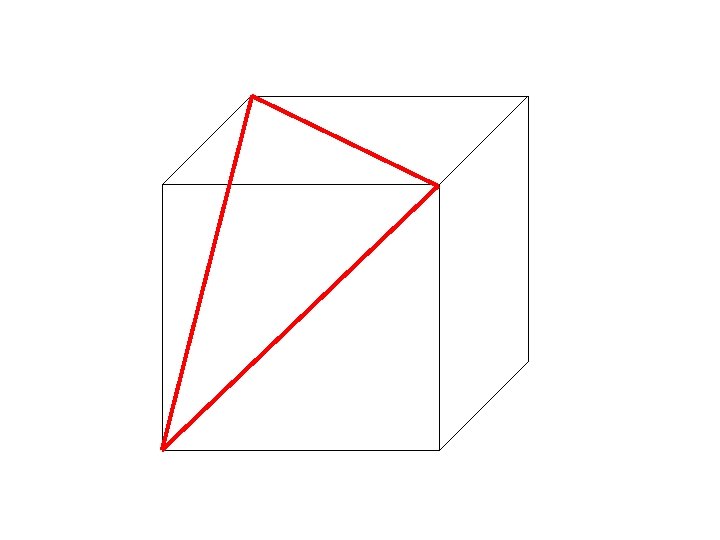
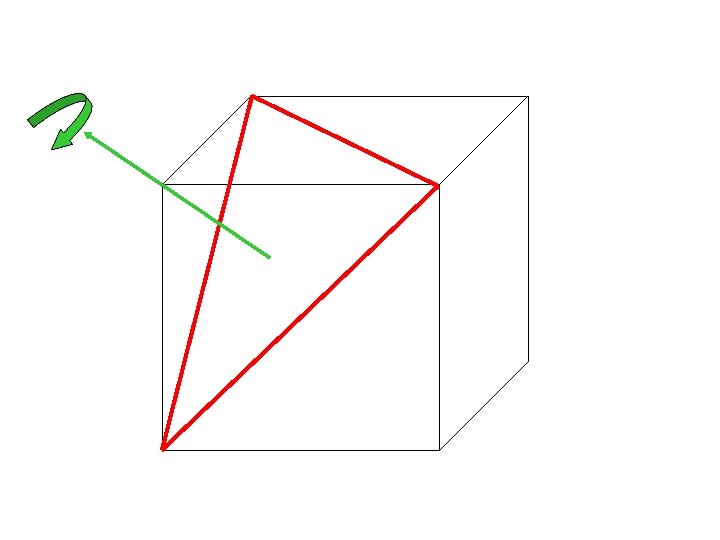
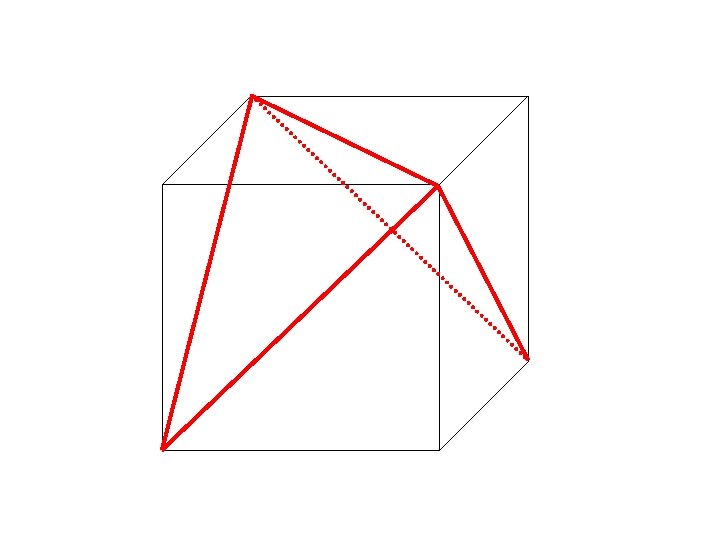
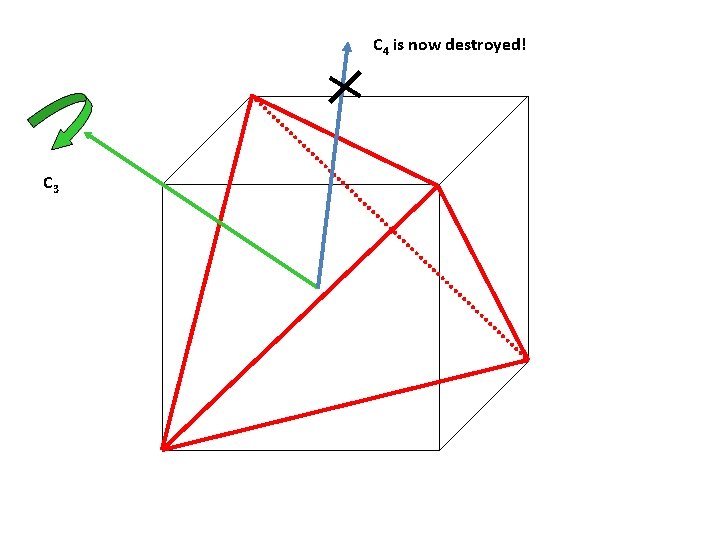
See any repeating relationship among the Cubic groups ? T: 4 C 3 and 3 C 2, mutually perpendicular Td (tetrahedral group): T + 3 S 4 axes + 6 sv O: 3 C 4 and 4 C 3, many C 2 Oh : 3 C 4 and 4 C 3, many C 2 + i + 3 sh + 6 sv Icosahedral group: Ih : 6 C 5, 10 C 3, 15 C 2, i, 15 sv How is the point symmetry of a cube related to an octahedron? How is the symmetry of an octahedron related to a tetrahedron? …. Let’s see!

C 4 C 3 C 4

C 3

C 4 C 3

C 4 C 3 C 4

C 4 is now destroyed! C 3