Today Imaging with coherent light Coherent image formation









- Slides: 40

Today Imaging with coherent light • Coherent image formation –space domain description: impulse response –spatial frequency domain description: coherent transfer function MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 1

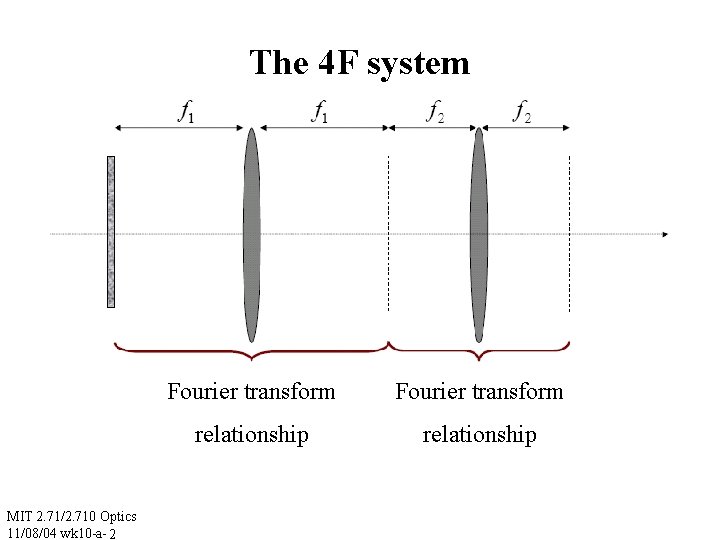
The 4 F system MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 2 Fourier transform relationship

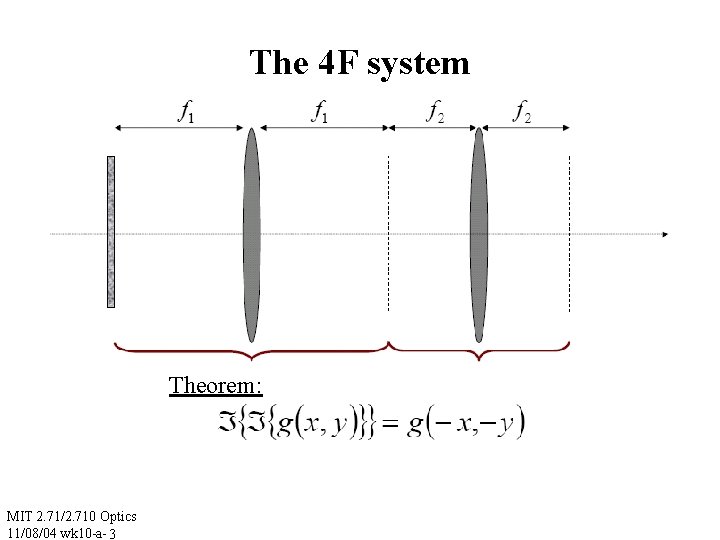
The 4 F system Theorem: MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 3

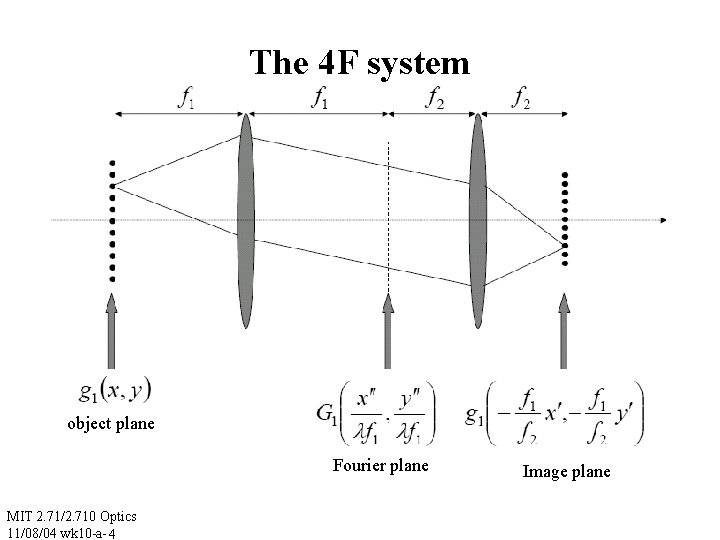
The 4 F system object plane Fourier plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 4 Image plane

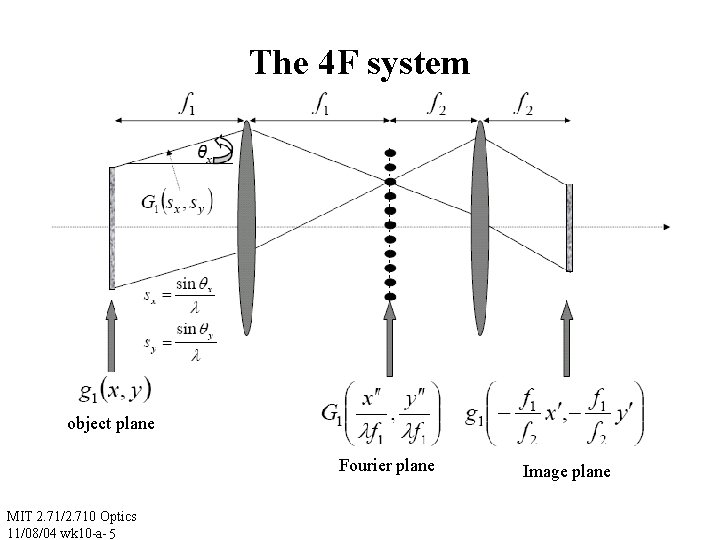
The 4 F system object plane Fourier plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 5 Image plane

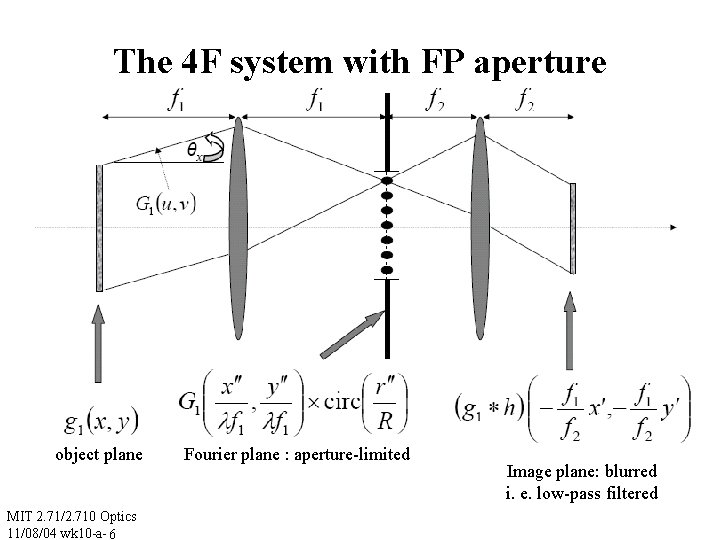
The 4 F system with FP aperture object plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 6 Fourier plane : aperture-limited Image plane: blurred i. e. low-pass filtered

Impulse response & transfer function A point source at the input plane. . . results not in a point image but in a diffraction pattern h(x’, y’) Point source at the origin ↔delta function δ(x, y) h(x’, y’) is the inpulse response of the system More commonly, h(x’, y’) is called the Coherent Point Spread Function (Coherent PSF) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 7

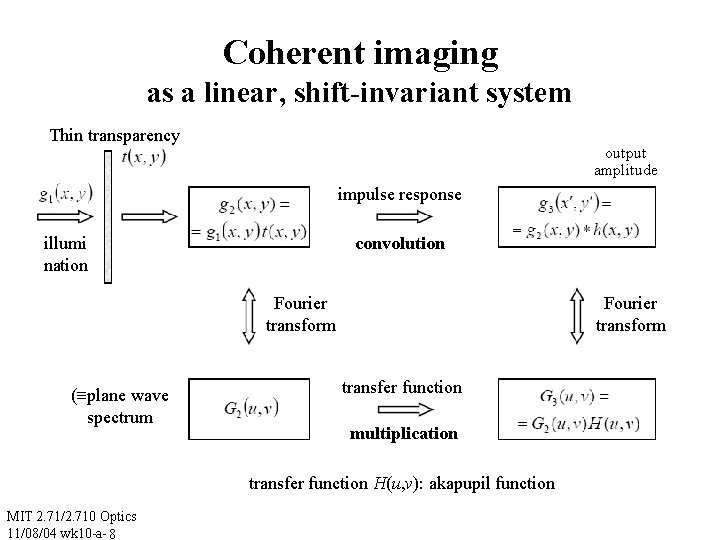
Coherent imaging as a linear, shift-invariant system Thin transparency output amplitude impulse response illumi nation convolution Fourier transform (≡plane wave spectrum Fourier transform transfer function multiplication transfer function H(u, v): akapupil function MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 8

Transfer function & impulse response of rectangular aperture Transfer function: circular aperture MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 9 Impulse response: Airy function

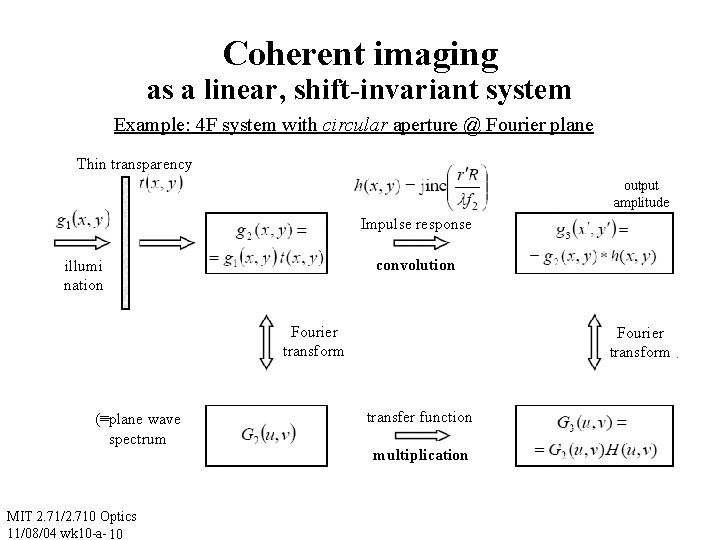
Coherent imaging as a linear, shift-invariant system Example: 4 F system with circular aperture @ Fourier plane Thin transparency output amplitude Impulse response convolution illumi nation Fourier transform (≡plane wave spectrum MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 10 Fourier transform transfer function multiplication

Transfer function & impulse response of rectangular aperture MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 11

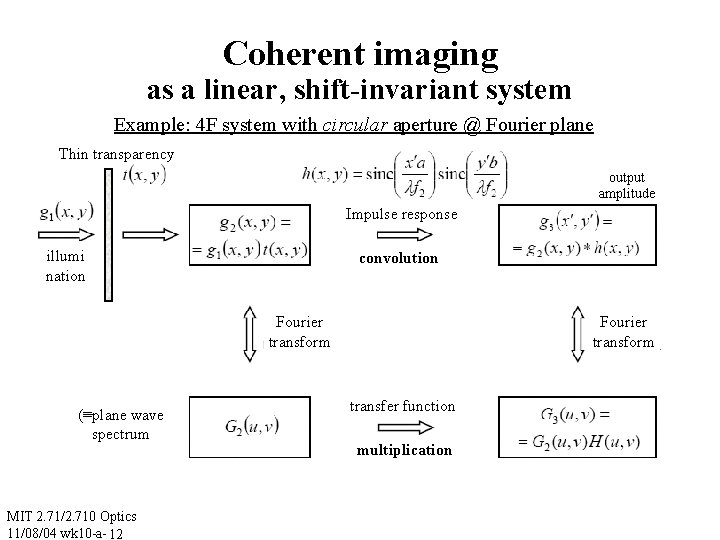
Coherent imaging as a linear, shift-invariant system Example: 4 F system with circular aperture @ Fourier plane Thin transparency output amplitude Impulse response illumi nation convolution Fourier transform (≡plane wave spectrum MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 12 Fourier transform transfer function multiplication

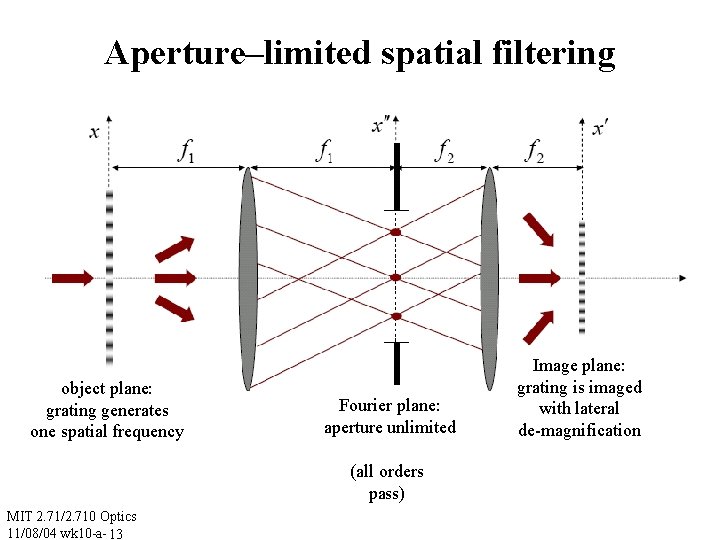
Aperture–limited spatial filtering object plane: grating generates one spatial frequency Fourier plane: aperture unlimited (all orders pass) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 13 Image plane: grating is imaged with lateral de-magnification

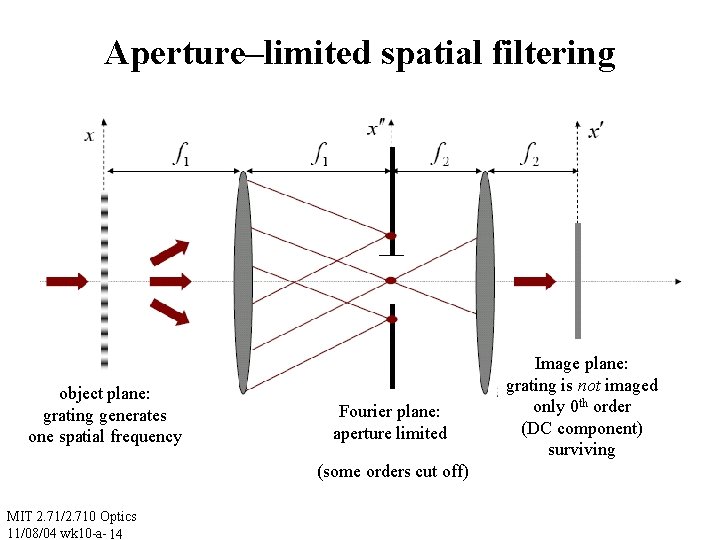
Aperture–limited spatial filtering object plane: grating generates one spatial frequency Fourier plane: aperture limited (some orders cut off) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 14 Image plane: grating is not imaged only 0 th order (DC component) surviving

Spatial frequency clipping field after input transparency field before filter field after filter field at output (image plane) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 15

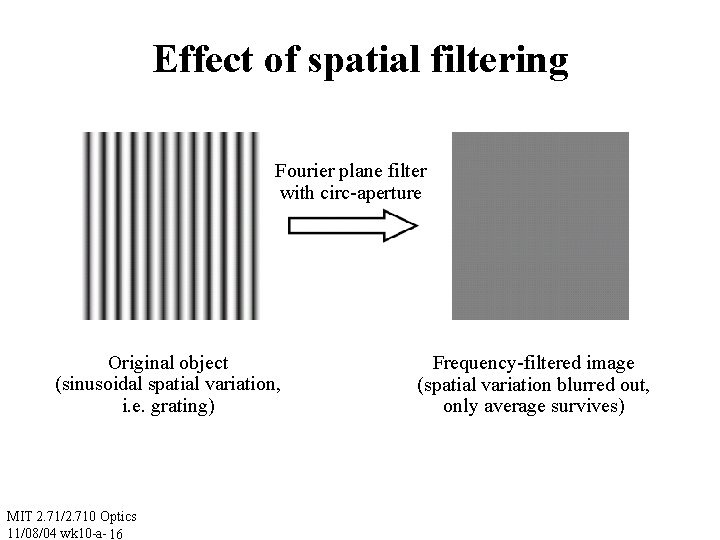
Effect of spatial filtering Fourier plane filter with circ-aperture Original object (sinusoidal spatial variation, i. e. grating) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 16 Frequency-filtered image (spatial variation blurred out, only average survives)

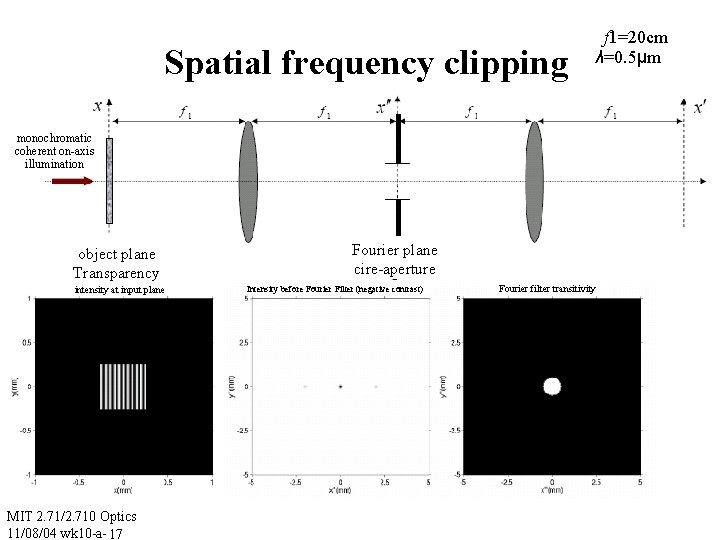
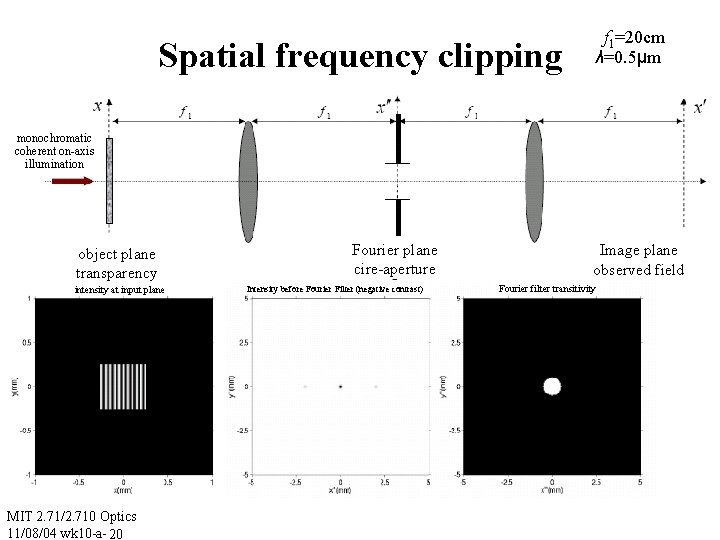
Spatial frequency clipping f 1=20 cm λ=0. 5μm monochromatic coherent on-axis illumination object plane Transparency intensity at input plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 17 Fourier plane cire-aperture Intensity before Fourier Filter (negative contrast) Fourier filter transitivity

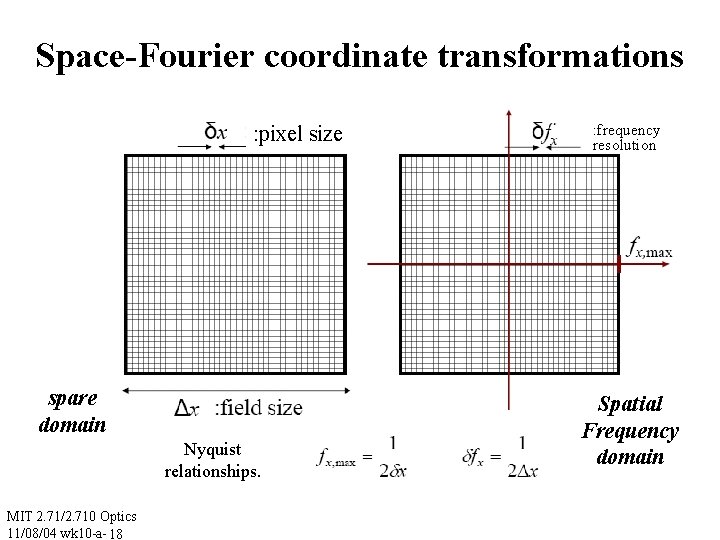
Space-Fourier coordinate transformations : pixel size spare domain Nyquist relationships. MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 18 : frequency resolution Spatial Frequency domain

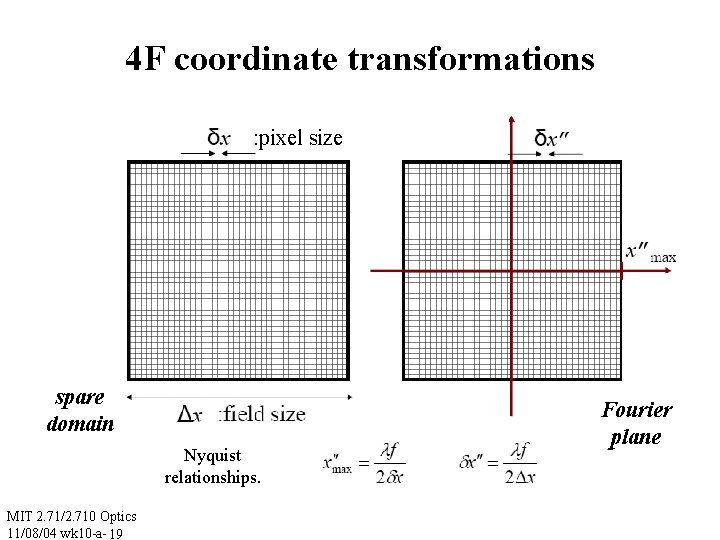
4 F coordinate transformations : pixel size spare domain Nyquist relationships. MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 19 Fourier plane

Spatial frequency clipping f 1=20 cm λ=0. 5μm monochromatic coherent on-axis illumination object plane transparency intensity at input plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 20 Fourier plane cire-aperture Intensity before Fourier Filter (negative contrast) Image plane observed field Fourier filter transitivity

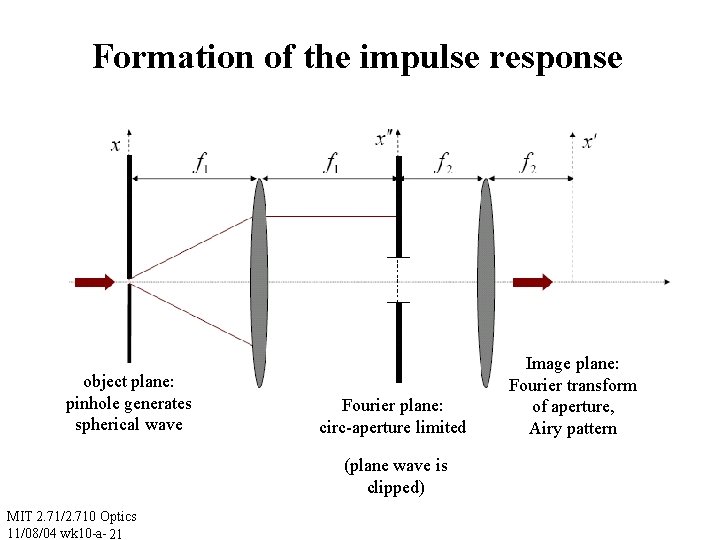
Formation of the impulse response object plane: pinhole generates spherical wave Fourier plane: circ-aperture limited (plane wave is clipped) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 21 Image plane: Fourier transform of aperture, Airy pattern

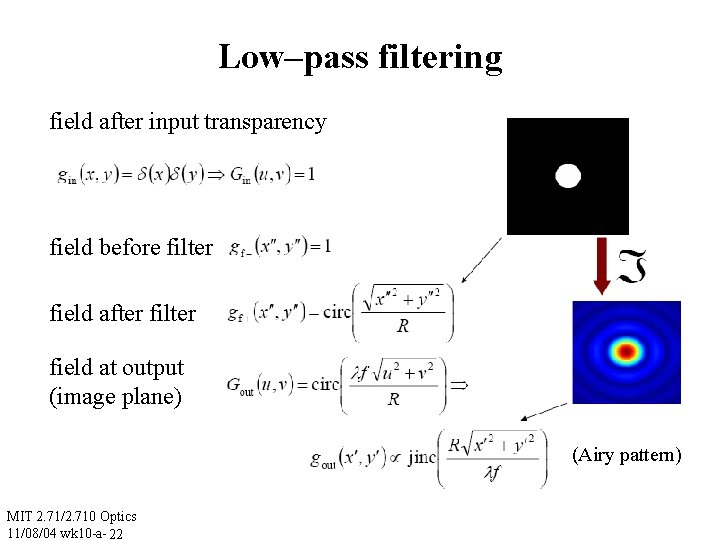
Low–pass filtering field after input transparency field before filter field after filter field at output (image plane) (Airy pattern) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 22

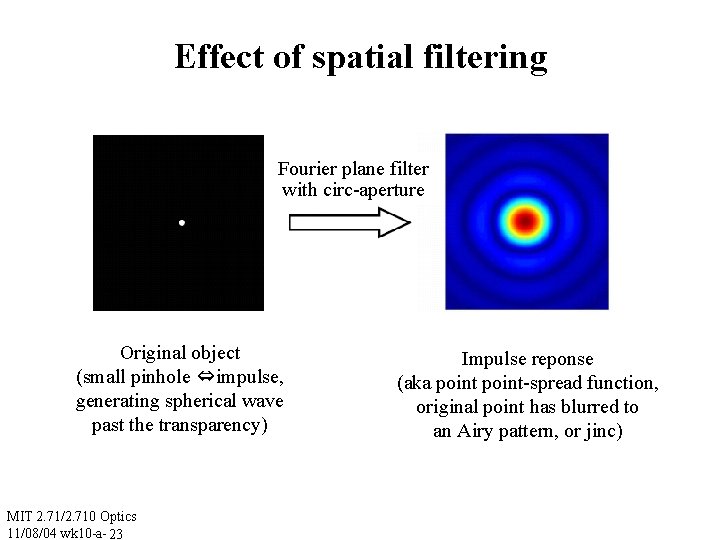
Effect of spatial filtering Fourier plane filter with circ-aperture Original object (small pinhole ⇔impulse, generating spherical wave past the transparency) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 23 Impulse reponse (aka point-spread function, original point has blurred to an Airy pattern, or jinc)

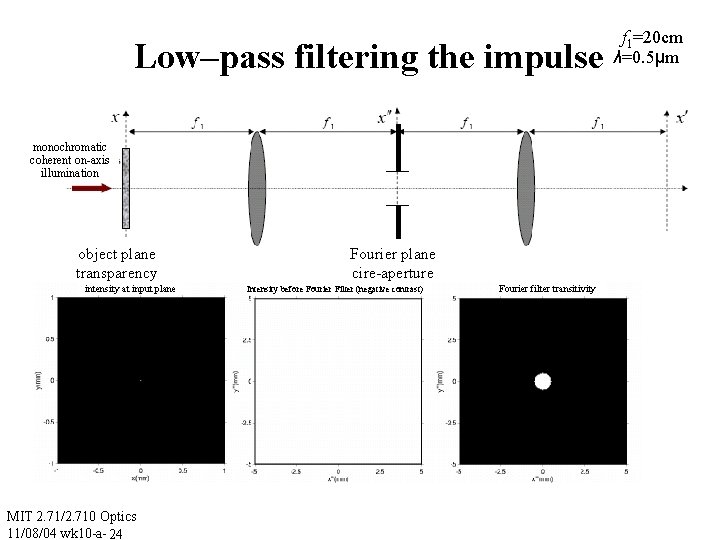
Low–pass filtering the impulse monochromatic coherent on-axis illumination object plane transparency intensity at input plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 24 Fourier plane cire-aperture Intensity before Fourier Filter (negative contrast) Fourier filter transitivity f 1=20 cm λ=0. 5μm

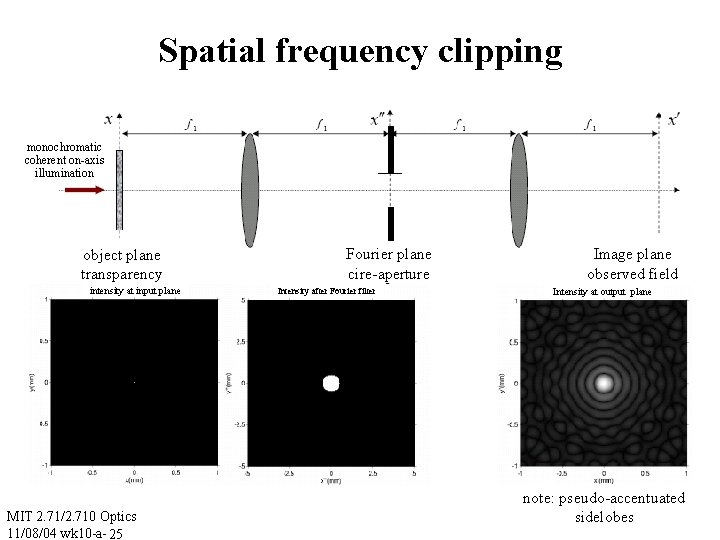
Spatial frequency clipping monochromatic coherent on-axis illumination object plane transparency intensity at input plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 25 Fourier plane cire-aperture Intensity after Fourier filter Image plane observed field Intensity at output plane note: pseudo-accentuated sidelobes

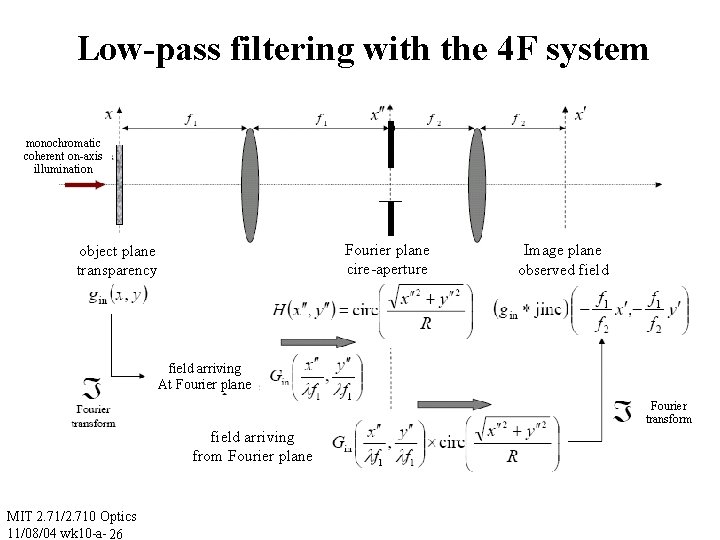
Low-pass filtering with the 4 F system monochromatic coherent on-axis illumination Fourier plane cire-aperture object plane transparency Image plane observed field arriving At Fourier plane Fourier transform field arriving from Fourier plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 26

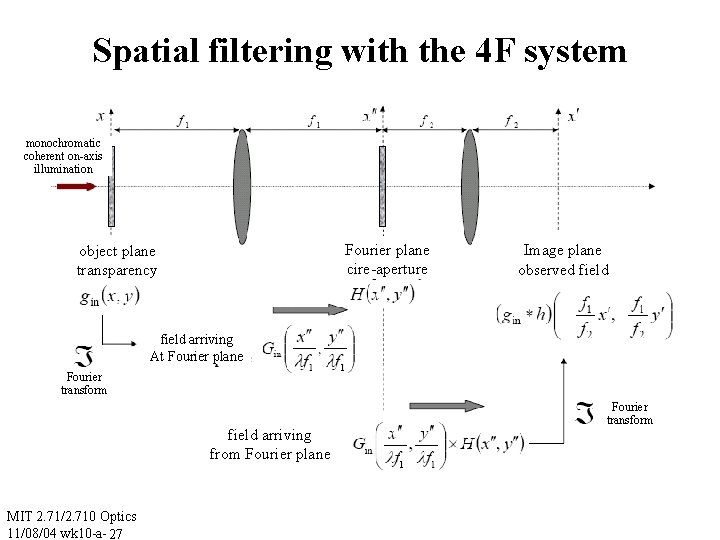
Spatial filtering with the 4 F system monochromatic coherent on-axis illumination Fourier plane cire-aperture object plane transparency Image plane observed field arriving At Fourier plane Fourier transform field arriving from Fourier plane MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 27 Fourier transform

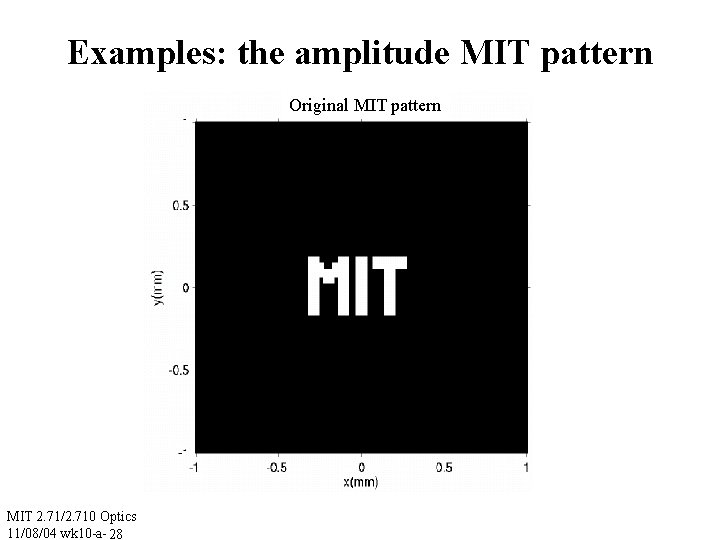
Examples: the amplitude MIT pattern Original MIT pattern MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 28

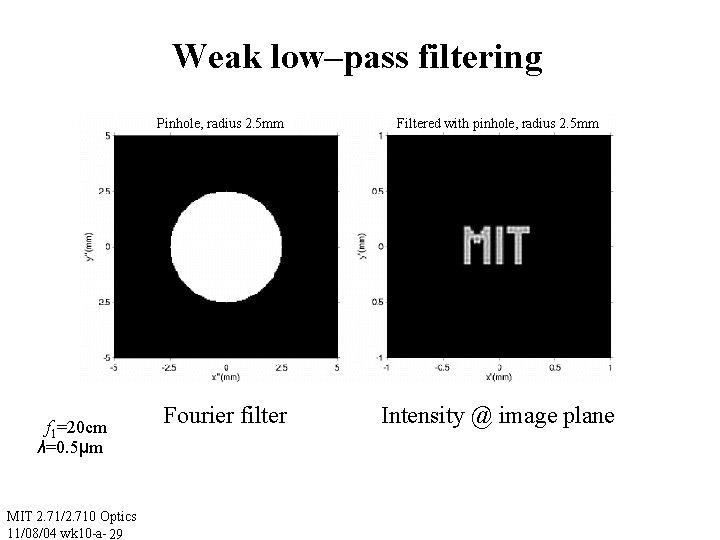
Weak low–pass filtering Pinhole, radius 2. 5 mm f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 29 Fourier filter Filtered with pinhole, radius 2. 5 mm Intensity @ image plane

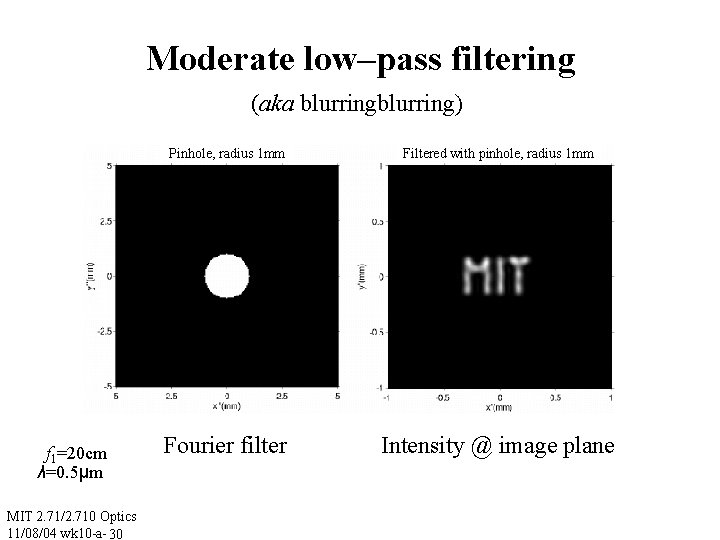
Moderate low–pass filtering (aka blurring) f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 30 Pinhole, radius 1 mm Filtered with pinhole, radius 1 mm Fourier filter Intensity @ image plane

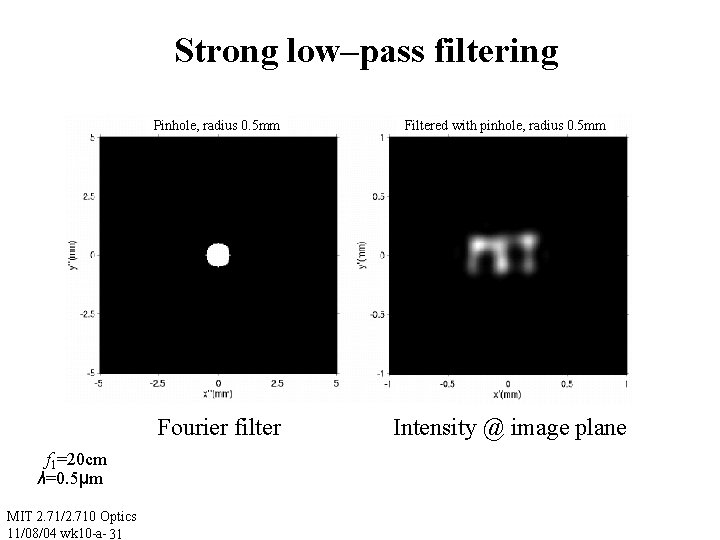
Strong low–pass filtering Pinhole, radius 0. 5 mm Fourier filter f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 31 Filtered with pinhole, radius 0. 5 mm Intensity @ image plane

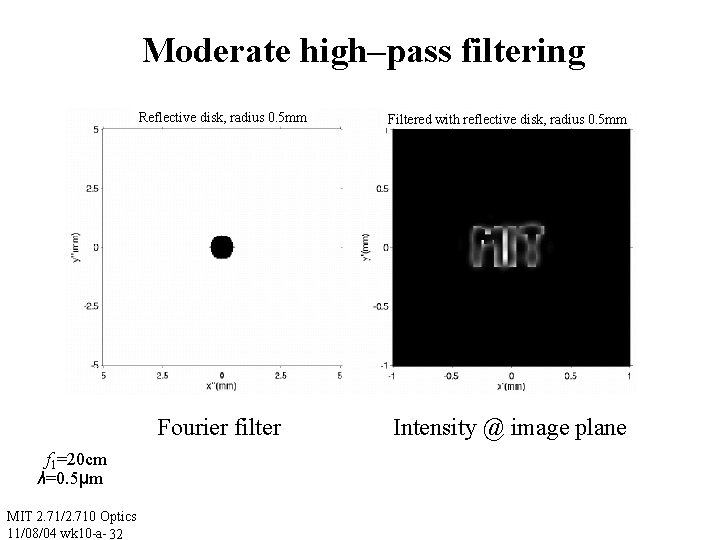
Moderate high–pass filtering f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 32 Reflective disk, radius 0. 5 mm Filtered with reflective disk, radius 0. 5 mm Fourier filter Intensity @ image plane

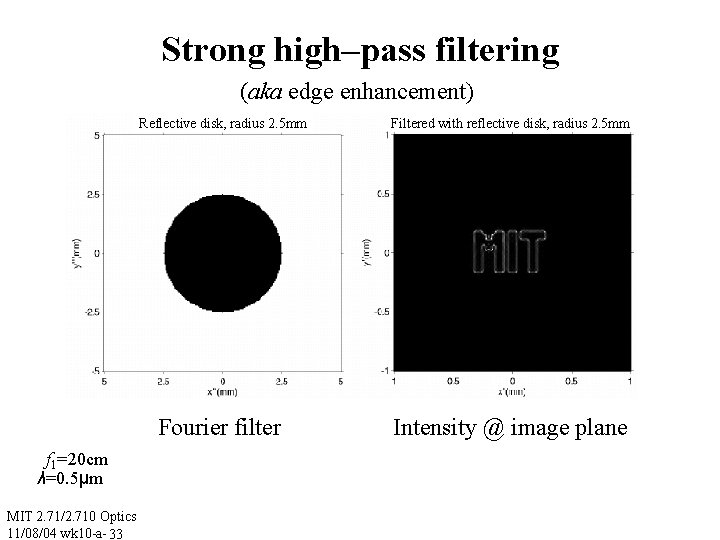
Strong high–pass filtering (aka edge enhancement) f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 33 Reflective disk, radius 2. 5 mm Filtered with reflective disk, radius 2. 5 mm Fourier filter Intensity @ image plane

1 -dimensional blurring f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 34 Horizontal slit, width 2 mm Filtered with horizontal slit, width 2 mm Fourier filter Intensity @ image plane

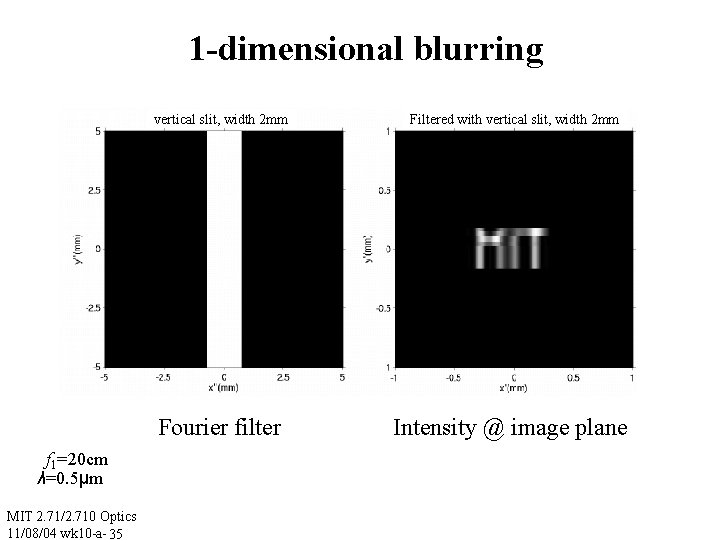
1 -dimensional blurring vertical slit, width 2 mm Fourier filter f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 35 Filtered with vertical slit, width 2 mm Intensity @ image plane

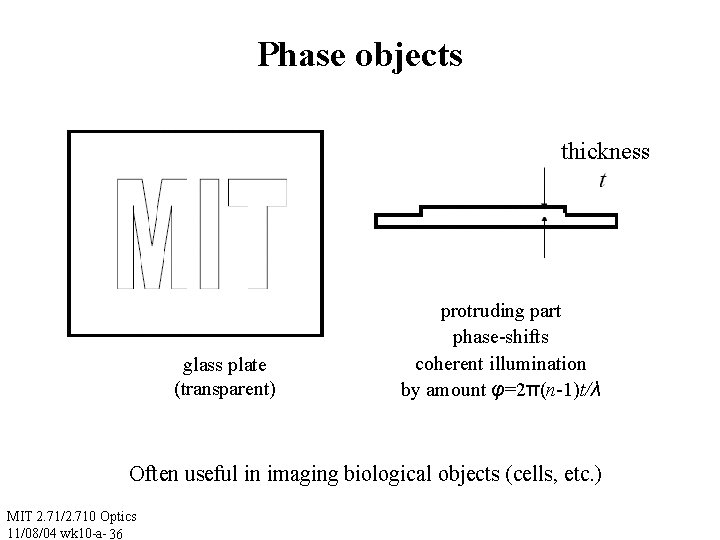
Phase objects thickness glass plate (transparent) protruding part phase-shifts coherent illumination by amount φ=2π(n-1)t/λ Often useful in imaging biological objects (cells, etc. ) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 36

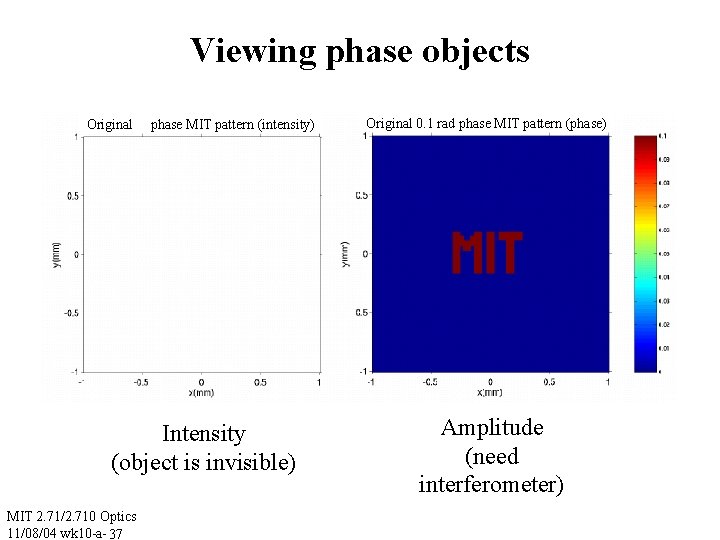
Viewing phase objects Original phase MIT pattern (intensity) Intensity (object is invisible) MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 37 Original 0. 1 rad phase MIT pattern (phase) Amplitude (need interferometer)

Zernicke phase-shift mask (magnitude), radii 5 mm & 1 mm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 38 phase-shift mask (phase), radii 5 mm & 1 mm (phase)

Imaging with Zernicke mask phase-shift mask (phase), radii 5 mm & 1 mm (phase) Fourier filter f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 39 Filtered with, phase-shift mask, radii 5 mm & 1 mm Intensity @ image plane

Imaging with Zernicke mask phase-shift mask (phase), radii 5 mm & 0. 1 mm (phase) Fourier filter f 1=20 cm λ=0. 5μm MIT 2. 71/2. 710 Optics 11/08/04 wk 10 -a- 40 Filtered with, phase-shift mask, radii 5 mm & 0. 1 mm Intensity @ image plane