Today Applications of suffix trees Substring problem Exact


Today �Applications of suffix trees �Substring problem (暖身) �“Exact string matching” revisited �Linearization of circular string (挪移乾坤) �Longest common substring (異中求同) 2

Application One Substring Problem (recap as a warm-up)

Substring Problem �Input: two strings P and S, �where S is allowed to be preprocessed in O(|S|) time. �Output: an occurrence of P in S. �Objective: done in O(|P|) time. 4
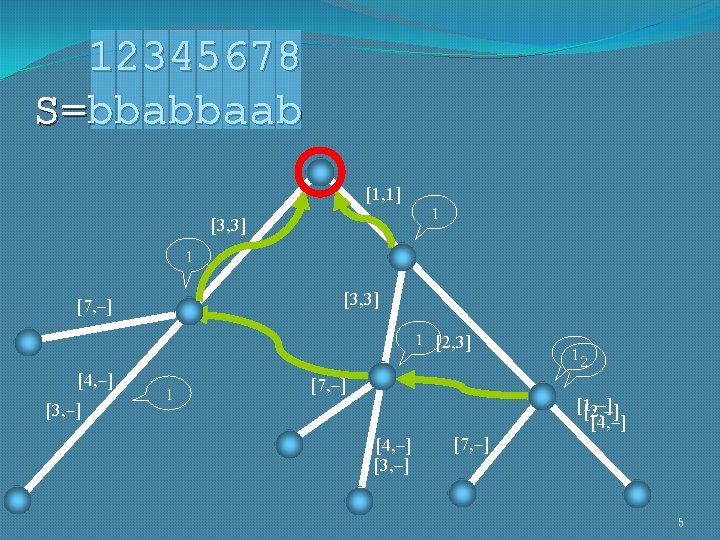
![12345678 S=bbabbaab Q: Where abba, baa, bb? [1, 1] [3, 3] [7, –] [3, 12345678 S=bbabbaab Q: Where abba, baa, bb? [1, 1] [3, 3] [7, –] [3,](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-6.jpg)
12345678 S=bbabbaab Q: Where abba, baa, bb? [1, 1] [3, 3] [7, –] [3, 3] [2, 3] [4, –] [7, –] 6
![12345678 S=bbabbaab Q: Where abba, baa, bb? [1, 1] [3, 3] 1 [3, 3] 12345678 S=bbabbaab Q: Where abba, baa, bb? [1, 1] [3, 3] 1 [3, 3]](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-7.jpg)
12345678 S=bbabbaab Q: Where abba, baa, bb? [1, 1] [3, 3] 1 [3, 3] [7, –] 3 6 [2, 3] [4, –] 1 [7, –] 2 [4, –] 5 3 [4, –] 2 [7, –] 4 1 7

Application Two Exact String Matching

Exact String Matching �Input: two strings P and S, �where S is allowed to be preprocessed in O(|S|) time. �Output: all occurrences of P in S. �Challenge: solving this in O(|P| + k) time, �where k is the number of occurrences of P in S. 9

Idea Each internal node keeps the labels of all its descendant leaves.
![12345678 S=bbabbaab Q: Something’s missing? [1, 1] [3, 3] 5, 2, 4, 1 [3, 12345678 S=bbabbaab Q: Something’s missing? [1, 1] [3, 3] 5, 2, 4, 1 [3,](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-11.jpg)
12345678 S=bbabbaab Q: Something’s missing? [1, 1] [3, 3] 5, 2, 4, 1 [3, 3] [7, –] 6, 3 6 Q: How do we fix this problem? [2, 3] [4, –] 4, 1 [7, –] 5, 2 [4, –] 5 3 [4, –] 2 [7, –] 4 1 11
![123456789 S=bbabbaab$ Q: Obtainable in O(|S|) time? [9, –] 9 [1, 1] [3, 3] 123456789 S=bbabbaab$ Q: Obtainable in O(|S|) time? [9, –] 9 [1, 1] [3, 3]](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-12.jpg)
123456789 S=bbabbaab$ Q: Obtainable in O(|S|) time? [9, –] 9 [1, 1] [3, 3] 6, 3, 7 6 3, 7 [4, –] [5, –] [9, –] [3, 3] [7, –] 3 5, 2, 4, 1, 8 [2, 3] [4, 4] 7 4, 1 [7, –] 1 [9, –] 8 5, 2 [4, –] 5 [4, –] 2 [7, –] 4 1 12

Perhaps not… �S = a a a $ 1, 2, 3, 4, 5 6 1, 2, 3, 4 5 1, 2, 3 4 1, 2 1 3 2 13

An observation �Consider the sequence L of leaves from left to right. The descendant leaves of each internal node has to be consecutive in L. 14
![123456789 S=bbabbaab$ L=637524189 [9, –] 9 [7, –] 5, 2, 4, 1, 8 [2, 123456789 S=bbabbaab$ L=637524189 [9, –] 9 [7, –] 5, 2, 4, 1, 8 [2,](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-15.jpg)
123456789 S=bbabbaab$ L=637524189 [9, –] 9 [7, –] 5, 2, 4, 1, 8 [2, 3] [4, 4] 2, 3 [5, –] 7 4, 5 [7, –] 3, 7 [9, –] [3, 3] 1, 3 6, 3, 7 6 3 4, 8 [1, 1] [3, 3] 8 6, 7 4, 1 5, 2 [4, –] 5 [4, –] 2 [7, –] 4 1 15


Application Three Circular String Linearization (挪移乾坤)
![Notation �Let 挪(S, i) denote the string S[i…|S|] S[1…i – 1]. i S 挪(S, Notation �Let 挪(S, i) denote the string S[i…|S|] S[1…i – 1]. i S 挪(S,](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-18.jpg)
Notation �Let 挪(S, i) denote the string S[i…|S|] S[1…i – 1]. i S 挪(S, i) 18

b b a a The problem �Input �a string S. �Output �an index i that maximizes the alphabetical order of 挪 (S, i). b a 挪(S, 1) 挪(S, 2) 挪(S, 3) 挪(S, 4) 挪(S, 5) 挪(S, 6) 挪(S, 7) 挪(S, 8) = = = = b b 12345678 bbabbaabb abbaabbba baabbbabb abbbabbaa 19

Naïve algorithm Time complexity? let j = 1; for i = 2 to |S| do { if (挪(S, i) > 挪(S, j)) { let j = i; } } output j; 20

Q: Can we beat O(|S|2)? b b b a a a b b 12345678 挪(S, 1) = b b a a b 挪(S, 2) = b a b b a a b b 挪(S, 3) = a b b a a b b b 挪(S, 4) = b b a a b b b a 挪(S, 5) = b a a b b b a b 挪(S, 6) = a a b b b a b b 挪(S, 7) = a b b b a 挪(S, 8) = b b b a a 21

Linear-Time Algorithm via Suffix Tree
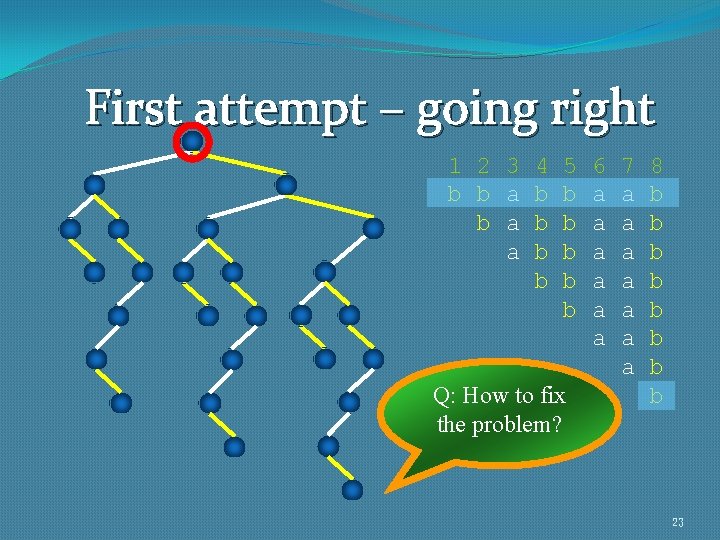
First attempt – going right 1 2 3 b b a a 4 b b 5 b b b Q: How to fix the problem? 6 a a a 7 a a a a 8 b b b b 23

Second Attempt Suffix tree for SS

Key observation �Each length-|S| substring of SS is a 挪(S, j) for some index j with 1≤ j ≤ |S|. �Each 挪(S, j) with 1≤ j ≤ |S| is a length-|S| substring of SS. 25
![1234567890123456 SS=bbabbaab [1, 1] 1 [3, 3] 1 [2, 2] [3, 3] [7, –] 1234567890123456 SS=bbabbaab [1, 1] 1 [3, 3] 1 [2, 2] [3, 3] [7, –]](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-26.jpg)
1234567890123456 SS=bbabbaab [1, 1] 1 [3, 3] 1 [2, 2] [3, 3] [7, –] [4, 5] [4, –] [3, –] [6, –] 1 [10, –] 1 [2, 3] 1 2 [10, –] 12 [3, 3] [7, –] [1, –] [2, –] [4, –] [3, –] [7, –] 12 345 26
![1234567890123456 SS=bbabbaab Q: How to use this suffix tree? [1, 1] [3, 3] [2, 1234567890123456 SS=bbabbaab Q: How to use this suffix tree? [1, 1] [3, 3] [2,](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-27.jpg)
1234567890123456 SS=bbabbaab Q: How to use this suffix tree? [1, 1] [3, 3] [2, 2] [3, 3] [7, –] [4, 5] [10, –] [3, 3] [7, –] [4, –] [6, –] [10, –] [4, –] [7, –] 27
![Equivalently, … �Output the index i such that SS[i…|SS|] corresponds to the rightmost leaf Equivalently, … �Output the index i such that SS[i…|SS|] corresponds to the rightmost leaf](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-28.jpg)
Equivalently, … �Output the index i such that SS[i…|SS|] corresponds to the rightmost leaf of the suffix tree for SS. �Clearly, this takes O(|S|) time. 28

Application Four Longest common substring (異中求同)

The problem �Input: two strings A and B. �Output: a longest string C that occurs in both A and B. �A �B �C �C = = = bbbabbaabbabbab bb baab abba bbabba 30

Naïve algorithm Time complexity? build suffix tree for B; for L = |A| downto 1 do for i = 1 to |A|-L+1 do { if A[i…i+L-1] occurs in B { output A[i…i+L-1] and halt; } } } output “no common substring”; 31
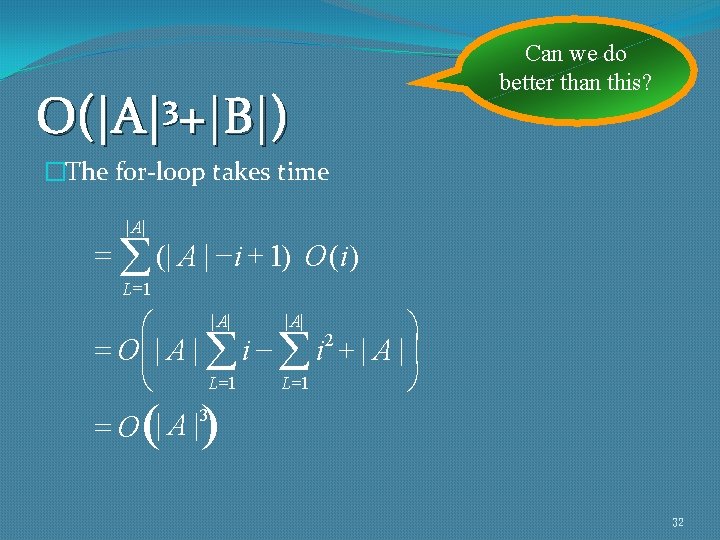
3 O(|A| +|B|) Can we do better than this? �The for-loop takes time | A| = å (| A | -i + 1) O (i ) L =1 | A| æ ö 2 = Oçç | A | å i - å i + | A | ç è ø L =1 = O | A |3 ( ) 32

A faster algorithm Time complexity? build suffix tree for B; for i = 1 to |A| do { find the largest integer L(i) such that A[i…i+L(i)-1] occurs in B by binary search; } output A[i…L(i)] for the i with the largest L(i); 33

2 O(|A| log|A|+|B|) �The for-loop takes O(|A|2 log|A|) time. �Each binary search takes time O(|A| log |A|). �There are overall O(|A|) binary searches. Can we do better than this? 34

Donald E. Knuth conjectured in 1970 that … it is impossible to solve this longest common substring problem in O(|A|+|B|) time.

Longest Common Substring in O(|A|+|B|) time via suffix tree

A-suffix A Idea # B $ B-suffix �Construct a suffix tree T for A#B$, where # and $ are two characters not in A and B. �There are exactly |A|+|B|+2 leaves in T, each leaf corresponds to a suffix of A#B$. �A-leaf: with label in {1, 2, …, |A|} � corresponds to an A-suffix. �B-leaf: with label in {|A|+2, …, |A|+|B|+1} � corresponds to a B-suffix. 37
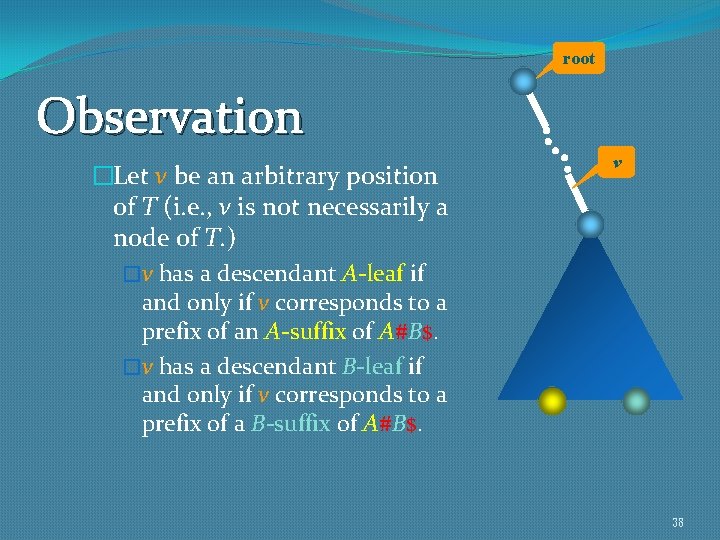
root Observation �Let v be an arbitrary position of T (i. e. , v is not necessarily a node of T. ) �v has a descendant A-leaf if and only if v corresponds to a prefix of an A-suffix of A#B$. �v has a descendant B-leaf if and only if v corresponds to a prefix of a B-suffix of A#B$. v 38

root Lemma �Let v be a position of T. �v has descendant A-leaf and B -suffix if and only if v corresponds to a common substring of A and B. v A-suffix A # B $ B-suffix 39

root Question v �Do we really need ‘#’ to separate A and B in the concatenated string A#B$? A-suffix A B $ B-suffix 40

The algorithm �Construct the suffix tree T of A#B$. �Output the string corresponding to a deepest internal node v such that the subtree of T rooted at v contains both A-leaf and B-leaf. �Q: why not checking leaves? �Q: why not checking positions of T that are not internal nodes of T? 41
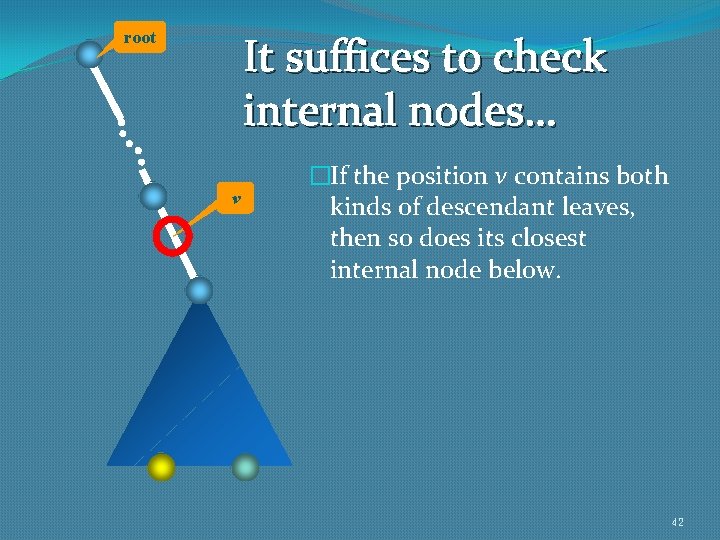
root It suffices to check internal nodes… v �If the position v contains both kinds of descendant leaves, then so does its closest internal node below. 42

Time = O(|A|+|B|) �O(|A|+|B|) time for constructing T. �O(|A|+|B|) time for marking the colors of each node, including each leaf and each internal nodes �O(|A|+|B|) time for computing the depths of all nodes �O(|A|+|B|) time to find a deepest internal node with both colors. 43

Space Complexity is also O(|A|+|B|). �Q: Can we further improve the time and space complexity? �“No” for the time complexity. �“Yes” for the space complexity. 44

Reducing the space to O(|A|)

Longest Common Substring �Input: two strings A and B. �Output: a longest string C that occurs in both A and B. �Objective: �O(|A|+|B|) time �O(|A|) space �Idea: �Construct the suffix tree of A only. 46

The algorithm �Construct the suffix tree T of A, keeping all the suffix links. �For i = 1 to |B| do �Find the largest integer 深(i) such that B[i…i+ 深(i)– 1] occurs in A. �Output B[i…i+深(i)– 1] where i is the index with maximum 深(i). 47

Naïvely, … �Finding 深(i) for each i takes O(深(i) +1) time by traversing T from the root. �But, all these |B| iterations may require Θ(|A||B|) time in total. depth = 深(i) 48
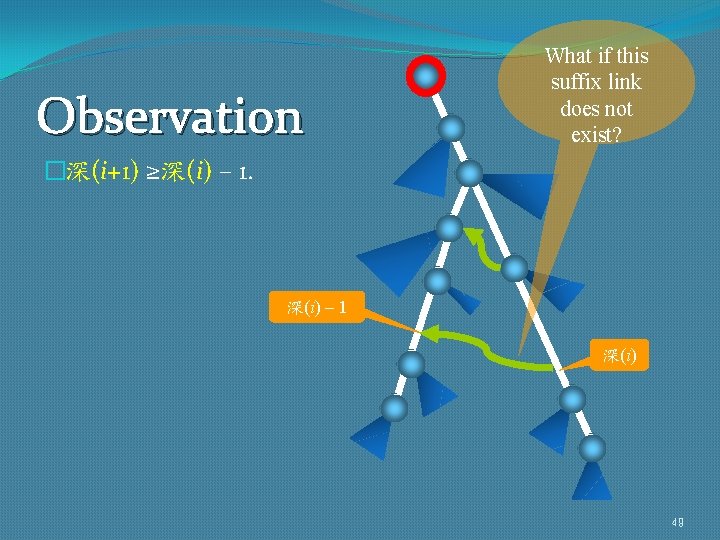
Observation What if this suffix link does not exist? �深(i+1) ≥深(i) – 1. 深(i) – 1 深(i) 49
![12345678 A=bbabbaab 12345678901 B=babaaba [1, 1] Record: 深(1) = 3 [3, 3] Record: 深(3) 12345678 A=bbabbaab 12345678901 B=babaaba [1, 1] Record: 深(1) = 3 [3, 3] Record: 深(3)](http://slidetodoc.com/presentation_image_h2/6099442f057d312e61c329b8efde78a1/image-50.jpg)
12345678 A=bbabbaab 12345678901 B=babaaba [1, 1] Record: 深(1) = 3 [3, 3] Record: 深(3) = 4 [2, 3] Record: 深(5) = 6 [3, 3] [7, 8] 6 1 [7, 8] [4, 8] 3 5 [4, 8] 1 2 [7, 8] 4 [4, 8] 1 50

Time and space �Clearly, the space complexity is O(|A|). �The time complexity still O(|A|+|B|). �We first show that the time is O(|A|+|B|) without considering that of suffix link traversal. � We then show that the time for suffix link traversal is also O(|A|+|B|). 51

Without considering suffix link traversal �The for-loop has exactly |B| iterations. �Suppose the i-th iteration moves the ↑arrow to the right by d(i) units. �d(1)+d(2)+…+d(|B|)=|B|, �because the ↑ arrow never goes left. �The i-th iteration takes time O(d(i)+1). �So, the overall time complexity is O(|B|). 52
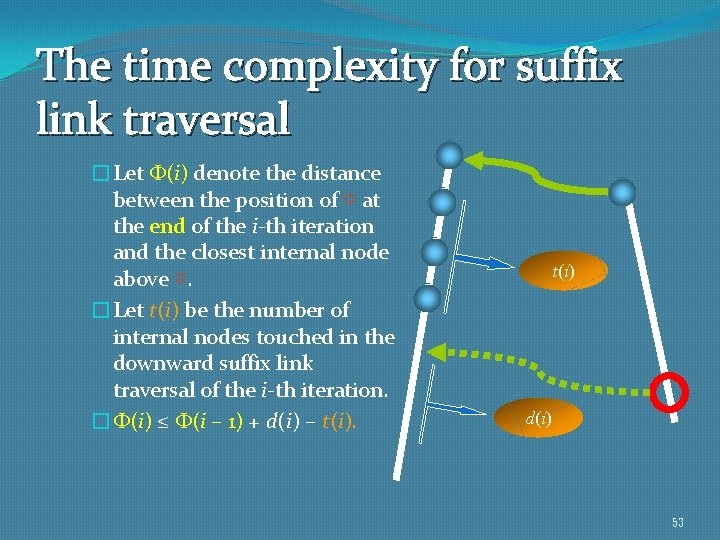
The time complexity for suffix link traversal �Let (i) denote the distance between the position of ○ at the end of the i-th iteration and the closest internal node above ○. �Let t(i) be the number of internal nodes touched in the downward suffix link traversal of the i-th iteration. � (i) ≤ (i – 1) + d(i) – t(i) d(i) 53

(i) ≤ (i – 1) + d(i) – t(i) �t(i) ≤ (i – 1) + d(i) – (i) �Therefore, t(1)+t(2)+…+t(|B|) is at most d(1)+d(2)+…+d(|B|) + (0) – (|B|), which is clearly O(|B|+|A|). � (0) ≤ |A|, and �d(1)+d(2)+…+d(|B|) = |B|. 54
- Slides: 54