To start A meter rule pivoted at its
- Slides: 13
To start A meter rule, pivoted at its centre of mass, supports a 3. 0 N weight at its 5. 0 cm mark, a 2. 0 N weight at its 25 cm mark and a weight W at its 80 cm mark. a) Sketch a diagram of the situation b) calculate the weight W
A LEVEL PHYSICS Year 1 Advanced Moments A* A B C • I can calculate the support force when a single support is in operation (Grade d) • I can calculate force on either support when two supports are in place (Grade b) • I can describe what is meant by a couple (Grade c)
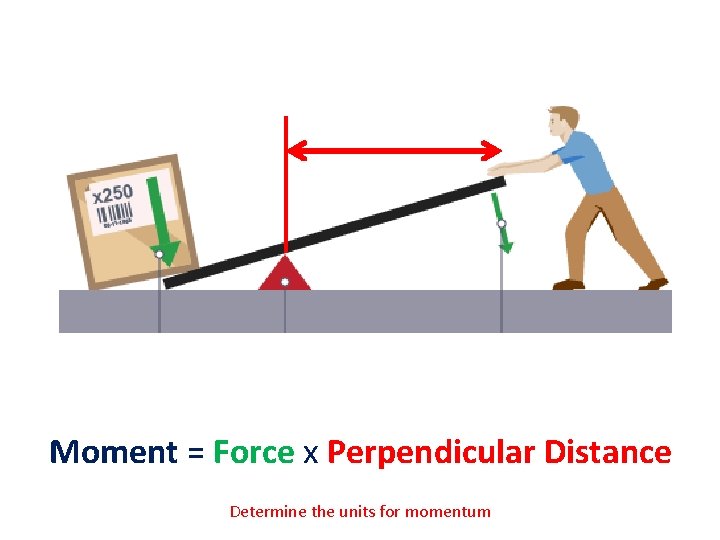
Moment = Force x Perpendicular Distance Determine the units for momentum
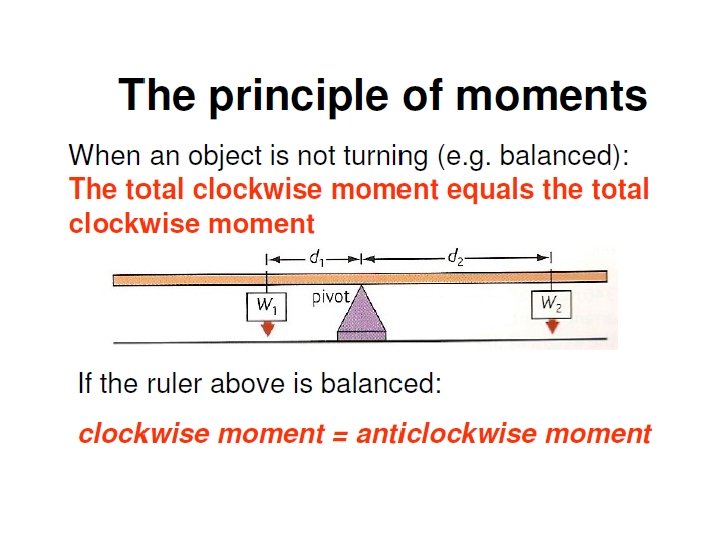
Support force is equal to the weight of the object (i. e. ruler) plus the weight of any object place upon it. S = W 1 + W 2 + Wo It is the reaction force of the object on the pivot.
A 30 cm ruler of 10 N is balanced on a knife edge with a 0. 5 kg mass on the 5 cm mark and a 0. 75 kg mass on the 27 cm mark. a) Draw a diagram b) Calculate the support (reaction) force
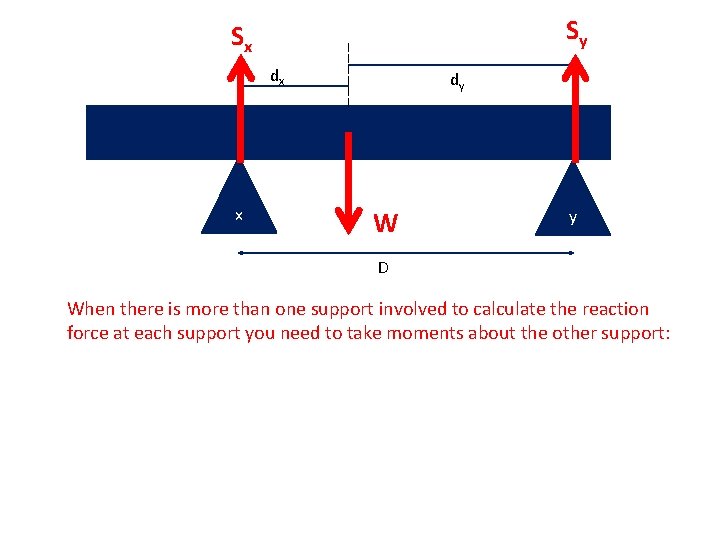
Sy Sx dx x dy W y D When there is more than one support involved to calculate the reaction force at each support you need to take moments about the other support:
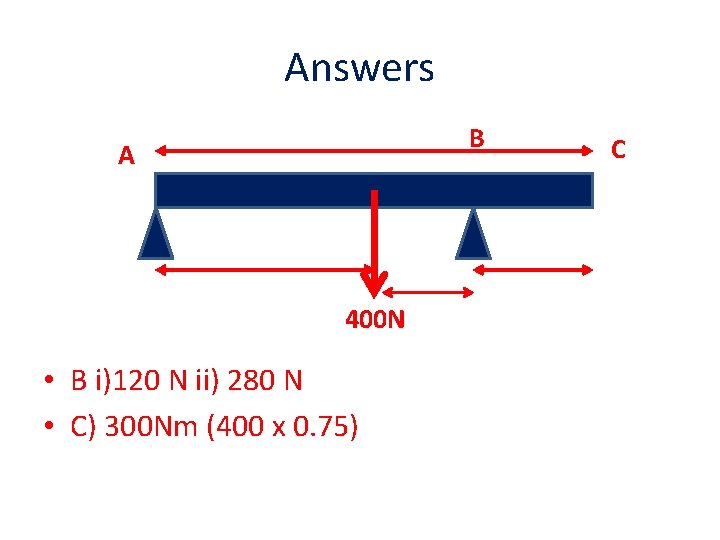
A uniform ladder of weight 400 N and length 3. 5 m is held horizontally by two people. One person supports the ladder at end A and the other supports it at point B, a distance of 1. 0 m from C (the opposite end to A). a) Draw the set up and the three forces b) Calculate the supporting force provided by the person at i) A ii) B c) The person at A releases the ladder. Calculate the moment which the person at B must provide to keep the ladder horizontal
Answers B A 400 N • B i)120 N ii) 280 N • C) 300 Nm (400 x 0. 75) C
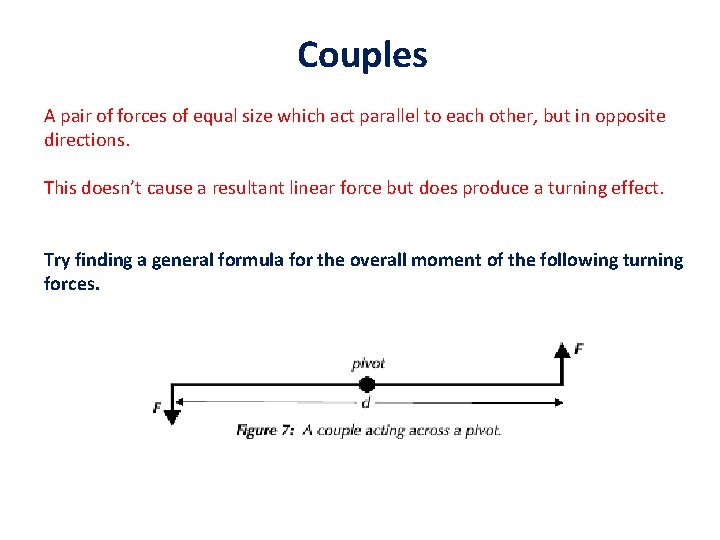
Couples A pair of forces of equal size which act parallel to each other, but in opposite directions. This doesn’t cause a resultant linear force but does produce a turning effect. Try finding a general formula for the overall moment of the following turning forces.
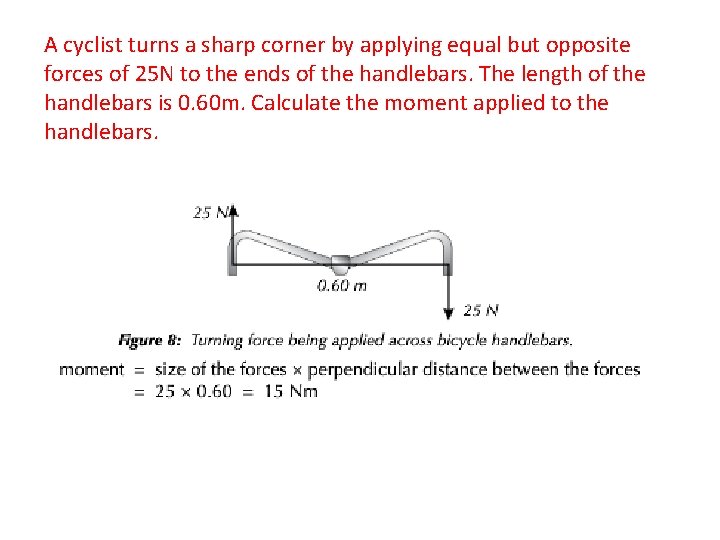
A cyclist turns a sharp corner by applying equal but opposite forces of 25 N to the ends of the handlebars. The length of the handlebars is 0. 60 m. Calculate the moment applied to the handlebars.
Exam questions worksheet
Next Lesson: Motion along a straight line Lesson after that: Motion along a straight line
Five hoops are each pivoted at a point on the rim
Five hoops are each pivoted at a point on the rim
Pivoted cradle balancing machine
Band and block brake
Pengertian tekanan zat padat
But we gotta start somewhere
Disaster triage
Its time to start running
The earliest start time rule
I comb its hair and love its shining eyes
When a train increases its velocity its momentum
Sunny windy cloudy rainy
If its square its a sonnet
Its halloween its halloween the moon is full and bright
