To solve complex problems involving Roman numerals Year

To solve complex problems involving Roman numerals. Year 5 - Number (GDS) Lesson 3

LI: To solve complex problems involving the Roman numerals. I can convert Roman numerals in to numbers I can use a written method to solve questions involving the four operations. I can give my answer as a Roman numeral. Recap from the last lesson… Look at the skills and then quickly check your understanding. Previously, we covered reading Roman numerals up to 1000 and recognising years written in Roman numerals. Vocabulary Numeral Value Digit I=1 V=5 X = 10 L = 50 C = 100 D = 500 M = 1000 Learning check: You do…. Let’s quickly recap how we can calculate equations with the four operations: Let’s take the following equation as an example: XXVII + LXXIV = The first thing we need to do is convert the Roman numerals into normal numbers so that we can use column method. So your equations should be rewritten like this: 27 + 74 = Secondly, we can add these numbers up in our heads or using column method: 27 + 54 = 81 Finally, we need to convert or 81 into Roman numerals. Remember we can always use our key vocabulary if we get stuck. So our final answer should look like this: XXVII + LXXIV = LXXXI QUESTIONS: Now Try to solve the following equations: a) DLXVIII + DXXIX b) MMCCV MCD c) XXII X XI

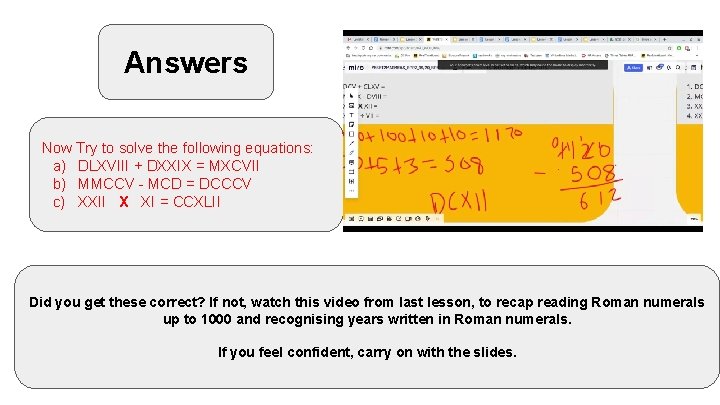
Answers Now Try to solve the following equations: a) DLXVIII + DXXIX = MXCVII b) MMCCV - MCD = DCCCV c) XXII X XI = CCXLII Did you get these correct? If not, watch this video from last lesson, to recap reading Roman numerals up to 1000 and recognising years written in Roman numerals. If you feel confident, carry on with the slides.

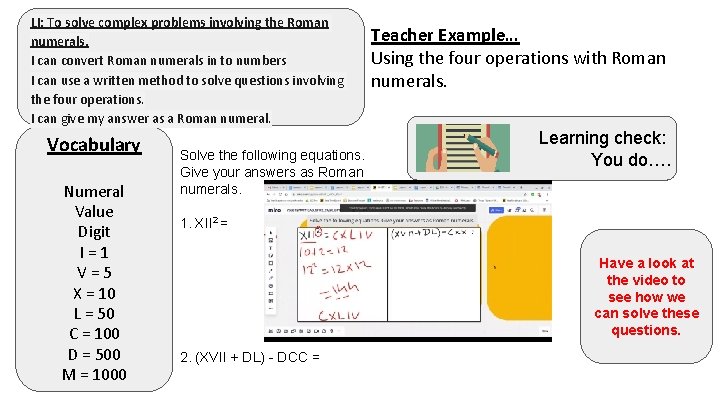
LI: To solve complex problems involving the Roman numerals. I can convert Roman numerals in to numbers I can use a written method to solve questions involving the four operations. I can give my answer as a Roman numeral. Vocabulary Numeral Value Digit I=1 V=5 X = 10 L = 50 C = 100 D = 500 M = 1000 Solve the following equations. Give your answers as Roman numerals. Teacher Example… Using the four operations with Roman numerals. Learning check: You do…. 1. XII 2 = Have a look at the video to see how we can solve these questions. 2. (XVII + DL) - DCC =

LI: To solve complex problems involving the Roman numerals. I can convert Roman numerals in to numbers I can use a written method to solve questions involving the four operations. I can give my answer as a Roman numeral. Vocabulary Numeral Value Digit I=1 V=5 X = 10 L = 50 C = 100 D = 500 M = 1000 Learning check: You do… Solve the following equations: Give your answers as Roman numerals. 1. XI 2 + LVI = 2. (MCM + CC) - D = 3. (ML ÷ X) + (CCLV - XXVII) = 4. IX 2 + CCCVI = Answers: 1. a) CLXXVII b) MDC c) CCCLXXVIII d) CCCLXXXVII

LI: To solve complex problems involving the Roman numerals. I can convert Roman numerals in to numbers I can use a written method to solve questions involving the four operations. I can give my answer as a Roman numeral. Vocabulary Numeral Value Digit I=1 V=5 X = 10 L = 50 C = 100 D = 500 M = 1000 Application question: Ken is playing a game. He has DCLX points. Then he scores another CCCLV points. Ken’s target is MD points. How many more points does Ken need to reach his target? Reasoning question: Amir has written down an equation below. Do you agree with his equation? Explain your reasoning. DCCLV + CCXLV = CCL X IV Teacher Example… Application and reasoning questions. . . Watch the video to see how we can solve this problem.

roundcomplex numbersproblems up to 10, 000 the. Roman nearest LI: To solve involvingtothe 10, 100 and 1000 numerals. I can identify nearest multiple a number convert the Roman numerals in totonumbers decide whether to round up orquestions round down I can use a written method to solve involving I canfour identify possibilities when rounding the operations. I can give my answer as a Roman numeral. Vocabulary Numeral Value Digit I=1 V=5 X = 10 L = 50 C = 100 D = 500 M = 1000 Learning check: You do…. Q 1 In a Rainforest, at the start of summer, there were MMCCLVI trees. After three weeks, DCXI trees were cut down. By the end of summer, DCCC trees were planted. How many trees were there by the end of summer? Q 2 A square kitchen has a perimeter of CXX metres. Alice argues that the area of the square kitchen must be CM metres squared. Is she correct?

LI: To solve complex problems involving the Roman numerals. I can convert Roman numerals in to numbers I can use a written method to solve questions involving the four operations. I can give my answer as a Roman numeral. Vocabulary Numeral Value Digit I=1 V=5 X = 10 L = 50 C = 100 D = 500 M = 1000 Learning check: Answers: Q 1 In a Rainforest, at the start of summer, there were MMCCLVI trees. After three weeks, DCXI trees were cut down. By the end of summer, DCCC trees were planted. How many trees were there by the end of summer? 2445 or MMCDXLV Q 2 A square kitchen has a perimeter of CXX metres. Alice argues that the area of the square kitchen must be CM metres squared. Is she correct? Yes she is correct. This is because 120 divided by 4 (because a square has four equal sides) equal 30. In order to the find the area we must multiply 30 by 30 (because area = length X width) which gives an answer of 900 metres squared.

Well done! Now complete the worksheet below on the google doc. You can either write the answers on the google doc, or write it out on paper and send a picture of your work to your teacher. https: //docs. google. com/document/d/13 cn 3 Juls. V-Okpj 3 U 6 k. UPLGnfk_41 je. Je. Dvnm. EVQKl 5 k/edit Remember to log onto maths whizz as well this week!