Titration of Mixtures of Acids Using a Strong

Titration of Mixtures of Acids Using a Strong Base For two acids to titrate separately, the ka of the stronger one should be at least 104 times greater than the other. If this condition is not satisfied, an end point will be observed. Always, the stronger acid will be titrated first since it suppresses the dissociation of the weaker one. 1

Example Find the p. H of a 50 m. L solution containing 0. 10 M HCl and 0. 10 M HOAc (ka = 1. 75 x 10 -5) after addition of 0, 25, 50, 75, 100, and 150 m. L of 0. 10 M Na. OH. Solution 1. After addition of 0 m. L Na. OH The solution contains a mixture of HCl and HOAc. We have seen earlier that HOAc dissociation will be suppressed in presence HCl and the p. H can be calculated as follows: HOAc D H+ + OAc 2

Ka = (0. 10 + x) x/(0. 10 – x) Assume 0. 10 >> x since ka is small 1. 75 x 10 -5 = 0. 10 x/0. 10 x = 1. 75 x 10 -5 Relative error = (1. 75 x 10 -5/0. 10) x 100 = 1. 8 x 10 -2% Therefore [H+] = 0. 10 + 1. 8 x 10 -5 = 0. 1 p. H = 1. 0 It is clear that all H+ comes from the strong acid. 3

2. After addition of 25 m. L Na. OH initial mmol HCl = 0. 10 x 50 = 5. 0 mmol Na. OH added = 0. 10 x 25= 2. 5 mmol HCl left = 5. 0 – 2. 5 = 2. 5 [H+]HCl = 2. 5/75 [HOAc] = 0. 10 x 50 / 75 = 5. 0/75 HOAc D H+ + OAc- 4

Ka = (2. 5/75 + x) x/((5. 0/75) – x) Assume 2. 5/75 >> x since ka is small 1. 75 x 10 -5 = 2. 5/75 x/(5. 0/75) x = 3. 5 x 10 -5 Relative error = (3. 5 x 10 -5/(2. 5/75)) x 100 = 0. 11% Therefore [H+] = 2. 5/75 + 5. 4 x 10 -5 = 2. 5/75 p. H = 1. 48 It is clear that all H+ still comes from the strong acid since dissociation of the weak acid is limited and in presence of strong acid the dissociation of the weak acid is further suppressed. 5

3. After addition of 50 m. L Na. OH Initial mmol HCl = 0. 10 x 50 = 5. 0 mmol Na. OH added = 0. 10 x 50 = 5. 0 mmol HCl left = 5. 0 – 5. 0 = ? ? This is the first equivalence point. At this point the HCl is over and the solution contains HOAc only and we should calculate the p. H of the solution from the h+ produced from dissociation of the HOAc. [HOAc] = 5. 0/100 = 0. 05 M HOAc D H+ + OAc 6

Ka = [H+][OAc-]/[HOAc] Ka = x * x / (0. 05 – x) Ka is very small. Assume 0. 05 >> x 1. 75*10 -5 = x 2/0. 05 x = 9. 4 x 10 -4 Relative error = (9. 4 x 10 -4/0. 05) x 100 = 1. 9% The assumption is valid and the [H+] = 9. 4 x 10 -4 M p. H = 3. 03 p. OH = 14 – 3. 03 = 10. 97 7

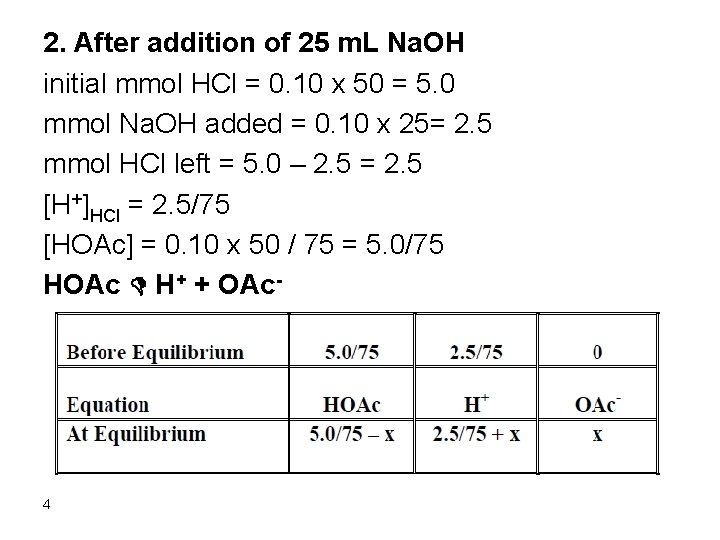
4. After addition of 75 m. L Na. OH Remember that 50 m. L of Na. OH were consumed in the reaction with HCl and thus only 25 m. L Na. OH will actually react with HOAc. Initial mmol HOAc = 0. 10 x 50 = 5. 0 Mmol Na. OH added = 0. 10 x 25 = 2. 5 m. L Mmpl HOAC left = 5. 0 – 2. 5 = 2. 5 [HOAc] = 2. 5/125 mmol OAc- formed = 2. 5 [OAc-] = 2. 5/125 Therefore, a buffer is formed and the p. H can be calculated as follows: HOAc D H+ + OAc 8

Ka = x (2. 5/125 – x)/ (2. 5/125 – x) Assume 2. 5/125 >> x 1. 75 x 10 -5 = x (2. 5/125)/2. 5/125 x = 1. 75 x 10 -5 Relative error = {1. 75 x 10 -5/(2. 5/125)} x 100 = 0. 088% The assumption is valid [H+] = 1. 75 x 10 -5 p. H = 4. 76 9

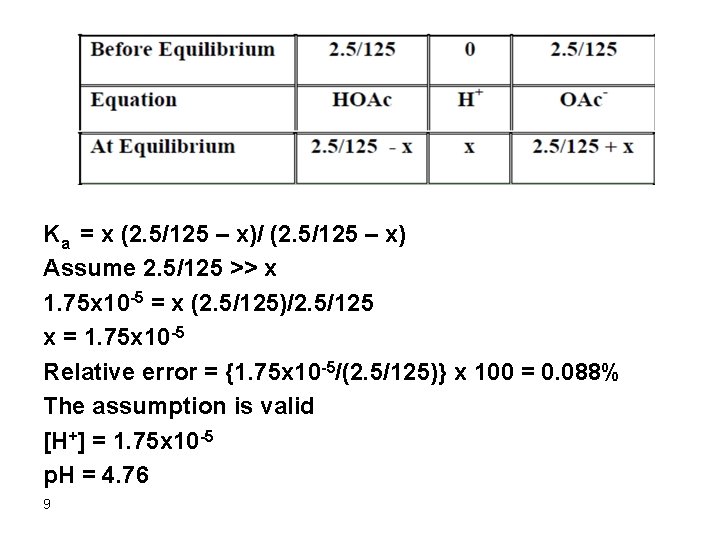
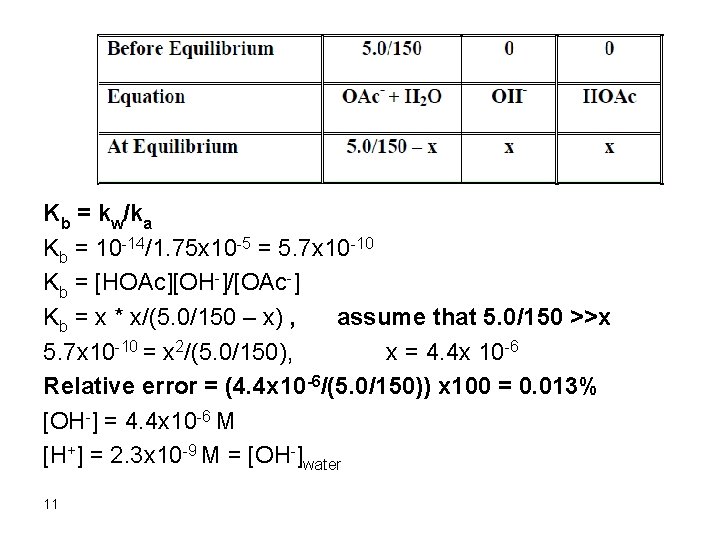
5. After addition of 100 m. L Na. OH Remember that 50 m. L of Na. OH were consumed in the reaction with HCl and thus only 50 m. L Na. OH will actually react with HOAc. Initial mmol HOAc = 0. 10 x 50 = 5. 0 Mmol Na. OH added = 0. 10 x 50 = 5. 0 m. L Mmol HOAC left = 5. 0 – 5. 0 = ? ? This is the second equivalence point mmol OAc- formed = 5. 0 [OAc-] = 5. 0/150 Therefore, we only have the salt where the p. H can be calculated as follows: OAc- + H 2 O D HOAc + OH 10

Kb = kw/ka Kb = 10 -14/1. 75 x 10 -5 = 5. 7 x 10 -10 Kb = [HOAc][OH-]/[OAc-] Kb = x * x/(5. 0/150 – x) , assume that 5. 0/150 >>x 5. 7 x 10 -10 = x 2/(5. 0/150), x = 4. 4 x 10 -6 Relative error = (4. 4 x 10 -6/(5. 0/150)) x 100 = 0. 013% [OH-] = 4. 4 x 10 -6 M [H+] = 2. 3 x 10 -9 M = [OH-]water 11

Therefore, the [OH-]acetate >> [OH-]water p. OH = 5. 36 p. H = 14 – 5. 36= 8. 64 6. After addition of 150 m. L Na. OH Remember that 50 m. L Na. OH were consumed in reaction with HCl and 50 m. L were consumed in reaction with HOAc. Therefore, we have added 50 m. L Na. OH in excess: mmol Na. OH excess = 0. 10 x 50 = 5. 0 [OH-] = 5. 0/200 = 0. 025 p. OH = 1. 6 p. H = 12. 4 12

Titration of a Mixture of Bases Using a Strong Acid The stronger base will be titrated first since most hydroxide comes from it. In a later stage, the weaker base will be titrated. Example Find the p. H of a 50 m. L solution containing 0. 10 M Na. OH and 0. 10 M Na 2 CO 3 (ka 1 = 4. 3 x 10 -7, ka 2 = 4. 8 x 10 -11) after addition of 0, 25, 50, 75, 100, 150, and 200 m. L of 0. 10 M HCl. 13

1. After addition of 0 m. L HCl The presence of Na. OH with carbonate suppresses the association of the carbonate with water and the OH- in solution will be mainly due to Na. OH. We can be sure of that by the following calculation: CO 32 - + H 2 O D HCO 3 - + OH- 14

Kb = 10 -14/4. 8 x 10 -11 = 2. 1 x 10 -4 Kb = (0. 10 + x) x/(0. 10 – x) Assume 0. 10>>x since kb is small 2. 1*10 -4= x x = 2. 1 x 10 -4 Relative error = (2. 1 x 10 -4/0. 10) x 100 = 0. 21% The assumption is valid. [OH-]CO 32 - = 2. 1 x 10 -4 M [OH-] = 0. 10 + 2. 1 x 10 -4 = 0. 1 p. OH = 1. 0 p. H = 14 -1. 0 = 13. 0 15

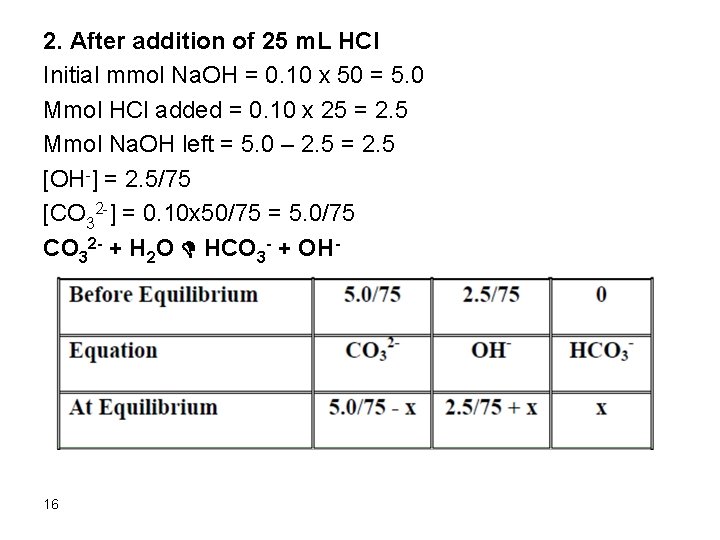
2. After addition of 25 m. L HCl Initial mmol Na. OH = 0. 10 x 50 = 5. 0 Mmol HCl added = 0. 10 x 25 = 2. 5 Mmol Na. OH left = 5. 0 – 2. 5 = 2. 5 [OH-] = 2. 5/75 [CO 32 -] = 0. 10 x 50/75 = 5. 0/75 CO 32 - + H 2 O D HCO 3 - + OH- 16

Kb = 10 -14/4. 8 x 10 -11 = 2. 1 x 10 -4 Kb = (2. 5/75 + x) x/((5. 0/75) – x) Assume 2. 5/75>>x since kb is small 2. 1*10 -4= (2. 5/75) x/(5. 0/75) x = 4. 2 x 10 -4 Relative error = (4. 2 x 10 -4/(2. 5/75)) x 100 = 1. 26% The assumption is valid. [OH-]CO 32 - = 4. 2 x 10 -4 M [OH-] = 2. 5/75 + 4. 2 x 10 -4 = 2. 5/75 Relative error = (4. 2 x 10 -4/(2. 5/75)) x 100 = 1. 26% [OH-] = 2. 5/75 p. OH = 1. 48 p. H = 14 -1. 48 = 12. 52 17

3. After addition of 50 m. L HCl Initial mmol Na. OH = 0. 10 x 50 = 5. 0 mmol HCl added = 0. 10 x 50 = 5. 0 mmol Na. OH left = 5. 0 – 5. 0 = 0 This is the first equivalence point where all the hydroxide is consumed and we have a solution of carbonate only. The p. H is calculated for that solution as follows: mmol CO 32 - = 0. 10 x 50 = 5. 0 [CO 32 -] = 5. 0/100 = 0. 05 CO 32 - + H 2 O D HCO 3 - + OH 18

Kb = 10 -14/4. 8 x 10 -11 = 2. 1 x 10 -4 Kb = x 2 /(0. 05 – x) Assume 0. 05 >> x since kb is small , x = 3. 2 x 10 -3 Relative error = (3. 2 x 10 -3/0. 05) x 100 = 6. 4% The assumption is invalid but I'll accept it and the [OH-] = 3. 2 x 10 -3 M p. OH = 2. 49 p. H = 14 -2. 49 = 11. 51 19

4. After addition of 75 m. L HCl The first 50 m. L were consumed in the reaction with Na. OH and only 25 m. L will react with the carbonate Initial mmol CO 32 - = 0. 10 x 50 = 5. 0 mmol HCl added = 0. 10 x 25 = 2. 5 mmol CO 32 - left = 5. 0 – 2. 5 = 2. 5 [CO 32 -] = 2. 5/125 mmol HCO 3 - formed = 2. 5 [HCO 3 -] = 2. 5/125 This is a buffer and the p. H of the solution could be calculated as follows: CO 32 - + H 2 O D HCO 3 - + OH 20

Kb = 10 -14/4. 8 x 10 -11 = 2. 1 x 10 -4 Kb = (2. 5/125 + x) x/(2. 5/125 – x) Assume 2. 5/125 >> x since kb is small , X = 2. 1 x 10 -4 Relative error = (2. 1 x 10 -4/(2. 5/125)) x 100 = 1. 1% The assumption is valid and [OH-] = 2. 1 x 10 -4 M p. OH = 3. 68 p. H = 14 – 3. 68 = 10. 32 21

5. After addition of 100 m. L HCl Remember that 50 m. L of HCl were consumed in the reaction with Na. OH. Therefore, only 50 m. L of added HCl will react with carbonate. mmol CO 32 - left = 0. 10 x 50 – 0. 10 x 50 = 0 This is a second equivalence point where all CO 32 - is converted to HCO 3 mmol HCO 3 - formed = 5. 0 [HCO 3 -] = 5. 0/150 M [H+] = {(ka 1 kw + ka 1 ka 2[HCO 3 -])/(ka 1 + [HCO 3‑]}1/2 [H+] = {(4. 3 x 10 -7 * 10 -14 + 4. 3 x 10 -7 * 4. 8 x 10 -11 *(5. 0/150))/(4. 3 x 10 -7 + (5. 0/150))}1/2 [H+] = 4. 5 x 10 -9 M p. H = 8. 34 22

6. After addition of 150 m. L HCl Remember that the first 50 m. L of HCl are needed to react with Na. OH, the second 50 m. L are required to convert CO 32 - into HCO 3 -. Therefore, only 50 m. L are available to react with the HCO 3 -. Initial mmol HCO 3 - = 5. 0 mmol HCl added = 0. 10 x 50 = 5. 0 mmol HCO 3 - left = 5. 0 – 5. 0 = 0 This is a third equivalence point where all HCO 3 - is converted to H 2 CO 3. The p. H can be calculated as follows mmol H 2 CO 3 formed = 5. 0 [H 2 CO 3] = 5/200 = 0. 025 23

H 2 CO 3 D H+ + HCO 3 ka 1 = 4. 3 x 10 -7 HCO 3 - D H+ + CO 32 ka 2 = 4. 8 x 10 -11 Since ka 1 is much greater than ka 2 Ka 1 = x * x/(0. 025 – x) Assume 0. 025>>x since ka 1 is small 4. 3*10 -7= x 2/0. 025, x = 1. 04 x 10 -4 Relative error = (1. 04 x 10 -4/0. 025) x 100 = 0. 41% The assumption is valid and [H+] = 1. 0 x 10 -4 M p. H = 4. 00 24

7. After addition of 200 m. L HCl Remember that 50 m. L of the added HCl will react with Na. OH, another 50 m. L of HCl will be consumed in converting the carbonate to bicarbonate. A third 50 m. L portion of HCl will be consumed in converting the bicarbonate to carbonic acid. We then have 50 m. L of excess HCl only mmol HCl = 0. 10 x 50 = 5. 0 [H+] = 5/250 = 0. 02 p. H = 1. 7 You should be able to calculate [H+]H 2 CO 3 25

Kjeldahl Analysis An application of acid-base titrations that finds an important use in analytical chemistry is what is called Kjeldahl nitrogen analysis. This analysis is used for the determination of nitrogen in proteins and other nitrogen containing compounds. Usually, the quantity of proteins can be estimated from the amount of nitrogen they contain. The Kjeldahl analysis involves the following steps: 26

1. Digestion of the nitrogen containing compound and converting the nitrogen to ammonium hydrogen sulfate. This process is accomplished by decomposing the nitrogen containing compound with sulfuric acid. 2. The solution in step 1 is made alkaline by addition of concentrated Na. OH which coverts ammonium to gaseous ammonia , and the solution is distilled to drive the ammonia out. 3. The ammonia produced in step 2 is collected in a specific volume of a standard acid solution (dilute) where neutralization occurs. 4. The solution in step 3 is back-titrated against a standard Na. OH solution to determine excess acid. 5. mmoles of ammonia are then calculated and related to mmol nitrogen. 27

Example A 0. 200 g of a urea (FW = 60, (NH 2)2 CO) sample is analyzed by the Kjeldahl method. The ammonia is collected in a 50 m. L of 0. 05 M H 2 SO 4. The excess acid required 3. 4 m. L of 0. 05 M Na. OH. Find the percentage of the compound in the sample. Solution 2 NH 3 + H 2 SO 4 = (NH 4)2 SO 4 mmol H 2 SO 4 reacted = mmol H 2 SO 4 taken – mmol H 2 SO 4 back-titrated 28

mmol H 2 SO 4 reacted = mmol H 2 SO 4 taken – mmol H 2 SO 4 back-titrated = 1/2 mmol Na. OH ½ mmol ammonia = mmol H 2 SO 4 reacted 1/2 mmol ammonia = 0. 05 x 50 – 1/2 x 0. 05 x 3. 4 mmol ammonia = 2(0. 05 x 50 – 1/2 x 0. 05 x 3. 4) mmol urea = 1/2 mmol ammonia mmol urea = 0. 05 x 50 – 1/2 x 0. 05 x 3. 4 = 2. 415 mg urea = 2. 415 x 60 = 144. 9 % urea = (144. 9/200)x 100 = 72. 5% 29

Modified Kjeldahl Analysis In conventional Kjeldahl method we need two standard solutions, an acid for collecting evolved ammonia and a base for back-titrating the acid. In a modified procedure, only a standard acid is required. In this procedure, ammonia is collected in a solution of dilute boric acid, the concentration of which need not be known accurately. The result of the reaction is the borate which is equivalent to ammonia. NH 3 + H 3 BO 3 g NH 4+ + H 2 BO 3 Boric acid is a very weak acid which is not titratable while borate is a strong base which can be titrated with a standard HCl solution. 30

Example A 0. 300 g feed sample is analyzed for its protein content by the modified Kjeldahl method. If 25 m. L of 0. 10 M HCl is required for the titration what is the percent protein content of the sample (mg protein = 6. 25 mg N). Solution mmol N = mmol HCl mmol N = 0. 10 x 25 = 2. 5 mmol N = 2. 5 mg N = 2. 5 x 14 = 35 mg protein = 35 x 6. 25 = 218. 8 % protein = (218. 8/300) x 100 = 72. 9% 31