Titration of amino acids The isoelectric point p

Titration of amino acids

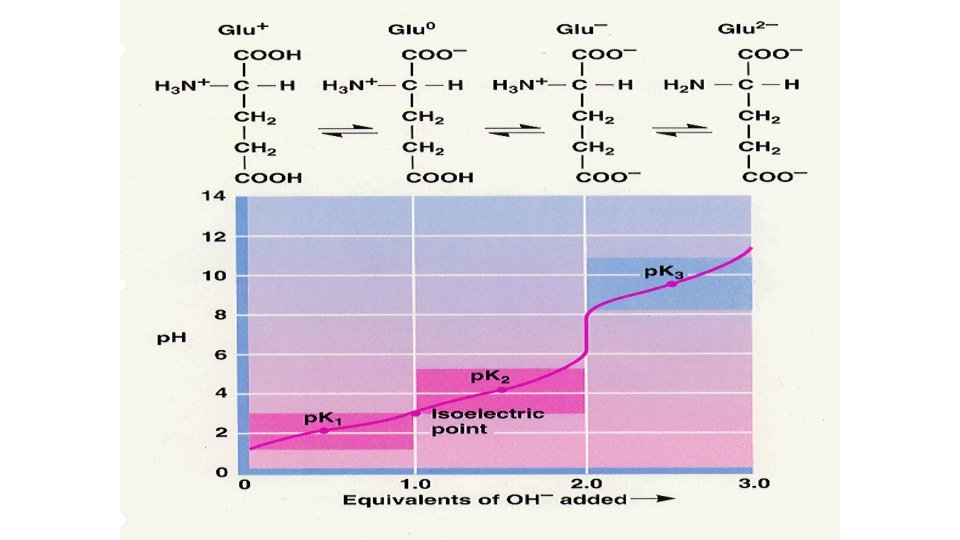
The isoelectric point (p. I) • the isoelectric point, p. I, is the p. H of an aqueous solution of an amino acid at which the molecules have no net charge. In other words, the positively charged groups are exactly balanced by the negatively charged groups. • For simple amino acids such as alanine, the p. I is an average of the p. Ka's of the carboxyl (2. 34) and ammonium (9. 69) groups. Thus, the p. I for alanine is calculated to be: (2. 34 + 9. 69)/2 = 6. 02. • If additional acidic or basic groups are present as side-chain functions, the p. I is the average of the p. Ka's of the two most similar acids. • The net charge on an amino acid—the algebraic sum of all the positively and negatively charged groups present—depends upon the p. Ka values of its functional groups and on the p. H of the surrounding medium.

Titration • Titration curves are produced by monitoring the p. H of given volume of a sample solution after successive addition of acid or alkali • The curves are usually plots of p. H against the volume of titrant added or more correctly against the number of equivalents added per mole of the sample • When an amino acid is dissolved in water it exists predominantly in the isoelectric form. • Upon titration with acid, it acts as a base, and upon titration with base, it acts as an acid( a compound that can act as either an acid or a base is known as an amphoteric compound).

+H +H - + HCl +H N-CH -COOH + Cl. N-CH -COO 3 2 (base) (acid) (1) - + Na. OH H N-CH -COO- + Na+ +H O N-CH -COO 3 2 2 (acid) (base) (2) These ionizations follow the Henderson-Hasselbalch equation: p. H= p. Ka+log [unprotonated form(base)] [protonated form (acid) ] When the conc of the unprotonated form equals that of the protonated form, the ratio of their concentrations equals 1, and log 1=0. • Hence, p. Ka can be defined as the p. H at which the concentrations of the protonated and unprotonated forms of a particular ionizable species are equal.

Acid–base properties • All of the amino acids have an acidic group (COOH) and a basic group (NH 2) attached to the α carbon. • Two of the amino acids have acidic side chains: aspartate and glutamate. • Three of the amino acids have basic side chains: arginine, histidine , and lysine. • All amino acids contain ionizable groups that act as weak acids or bases, giving off or taking on protons when the p. H is altered.

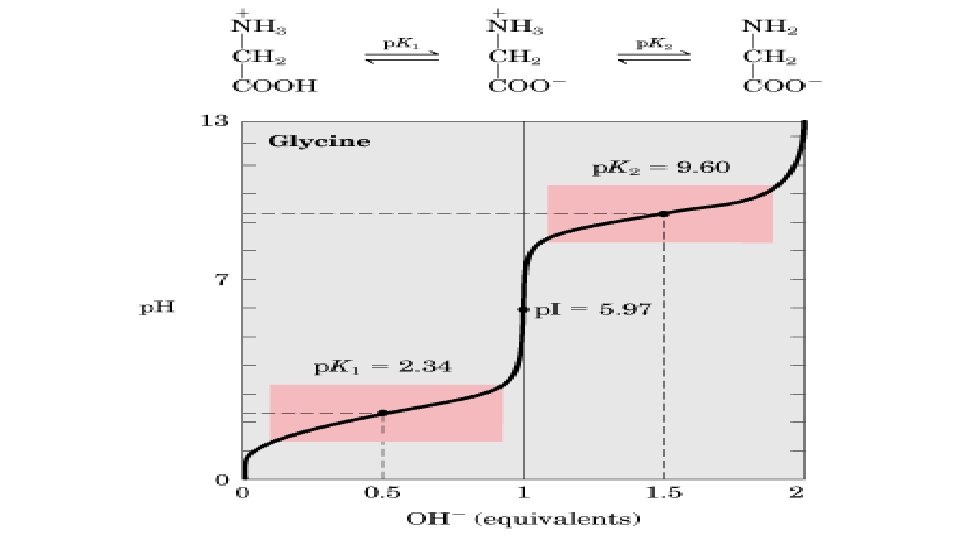
• Consider applying the Henderson-Hasselbalch equation to the titration of glycine with acid and base. • Glycine has two ionizable groups: a corboxyl group and an amino group, with p. Ka values of 2. 4 and 9. 6 respectively. • In water at p. H 6, glycine exists as a dipolar ion, or zwitterion, in which the carboxyl group is unprotonated(-COO- ) and the amino group is protonated to give the substituted ammonium ion(-NH 3+). • Addition of acid to the solution lowers the p. H rapidly at first and then more slowly. At p. H 2. 4 the p. Ka is reached, one-half the acid has been consumed, and the carboxyl group is half ionized and is most effective as a buffer. • Titration of the amino group with base follows a similar curve into the alkaline region. • The intersection between the titration of the carboxyl group and the titration of the amino group describes in this case the point at which glycine has no net charge, and is called the isoelectric point (p. I). •

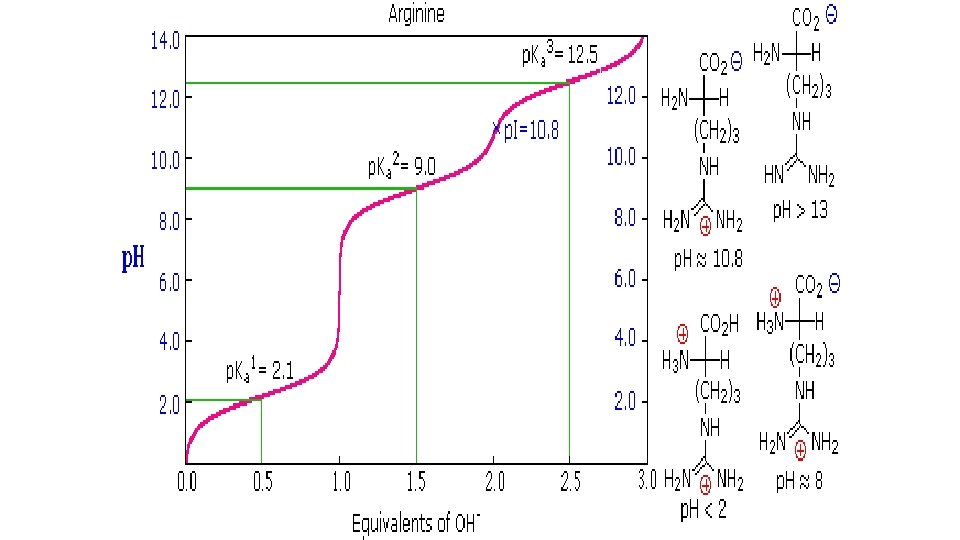
Cont. . (p. I) • In the case of aspartic acid, the similar acids are the alphacarboxyl function (p. Ka = 2. 1) and the side-chain carboxyl function (p. Ka = 3. 9), so p. I = (2. 1 + 3. 9)/2 = 3. 0. • For arginine, the similar acids are the guanidinium species on the side-chain (p. Ka = 12. 5) and the alpha-ammonium function (p. Ka = 9. 0), so the calculated p. I = (12. 5 + 9. 0)/2 = 10. 75.