Tirgul 11 Data Structures part 1 Stacks Queues

Tirgul 11 Data Structures part 1 (Stacks & Queues)

But first let’s do an exam question (OOP) 2

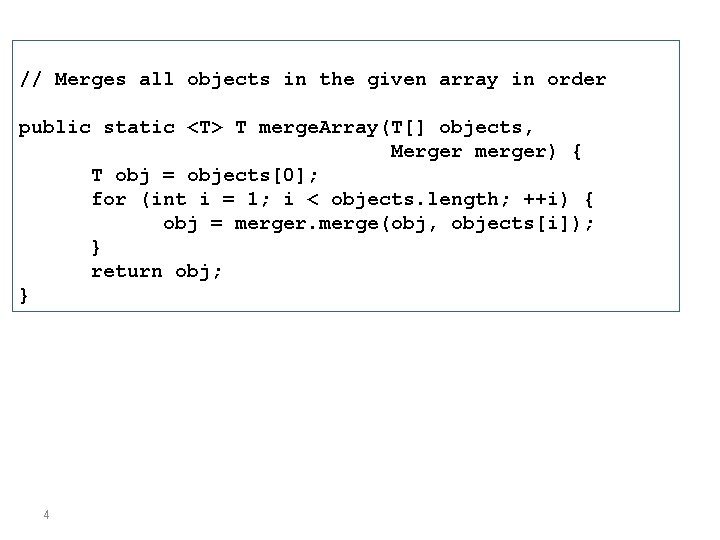
// Merges all objects in the given array in order public static <T> T merge. Array(T[] objects, Merger merger) { T obj = objects[0]; for (int i = 1; i < objects. length; ++i) { obj = merger. merge(obj, objects[i]); } return obj; } 4

(' נק 4). ב ומייצגת Resistor הממשק ( את implements) המממשת Simple. Resistor מחלקה כתבו : להיות צריכה ( המחלקה constructor) בנאי חתימת. כלשהי התנגדות בעל יחיד חשמלי נגד public Simple. Resistor(double resistance) /** * A simple resistor. */ public class Simple. Resistor implements Resistor { private double resistance; public Simple. Resistor(double resistance) { this. resistance = resistance; } public double resistance() { return resistance; } 5 }

/** * A resistor composed of two resistors. */ public abstract class Compound. Resistor implements Resistor{ protected Resistor resistor 1, resistor 2; public Compound. Resistor(Resistor resistor 1, Resistor resistor 2){ this. resistor 1 = resistor 1; this. resistor 2 = resistor 2; } } 7

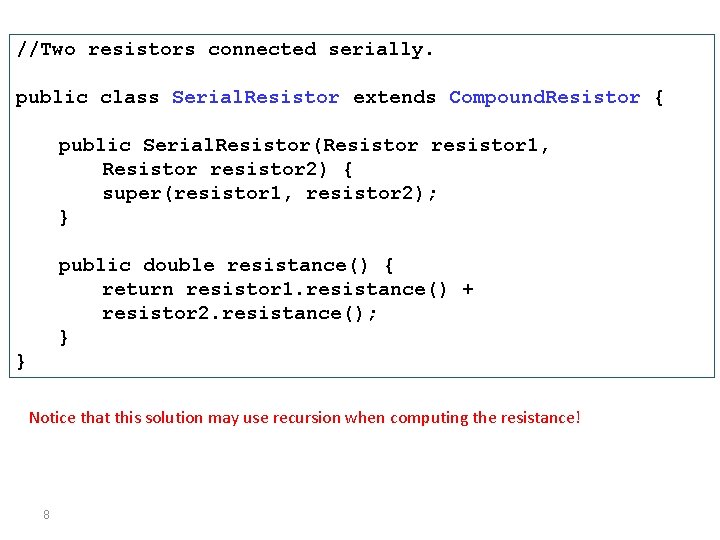
//Two resistors connected serially. public class Serial. Resistor extends Compound. Resistor { public Serial. Resistor(Resistor resistor 1, Resistor resistor 2) { super(resistor 1, resistor 2); } public double resistance() { return resistor 1. resistance() + resistor 2. resistance(); } } Notice that this solution may use recursion when computing the resistance! 8

//Two resistors connected in parallel. public class Parallel. Resistor extends Compound. Resistor { public Parallel. Resistor(Resistor resistor 1, Resistor resistor 2) { super(resistor 1, resistor 2); } public double resistance() { double r 1 = resistor 1. resistance(); double r 2 = esistor 2. resistance(); return (r 1 * r 2) / (r 1 + r 2); } } 9

(' נק 6). ה המממשות Serial. Resistor. Merger, Parallel. Resistor. Merger מחלקות שתי כתבו . בהתאמה , במקביל או בטור חיבורם ע"י התנגדות בעלי רכיבים שני וממזגות Merger הממשק את המממשים אובייקטים כפרמטרים מועברים הנ"ל במחלקות merge לשיטה קריאה שבכל להניח מותר . Resistor הממשק את public class Serial. Resistor. Merger implements Merger<Resistor> { public Resistor merge(Resistor obj 1, Resistor obj 2) { return new Serial. Resistor(obj 1, obj 2); } } public class Parallel. Resistor. Merger implements Merger<Resistor> { public Resistor merge(Resistor obj 1, Resistor obj 2) { return new Parallel. Resistor(obj 1, obj 2); } } 10

(' נק 6). ו : במקביל או בטור התנגדות בעלי רכיבים של מערך המחברות סטטיות שיטות שתי כתבו public static Resistor connect. Series(Resistor[] resistors) public static Resistor connect. Parallel(Resistor[] resistors) . ' א בסעיף שכתבתם בשיטה להשתמש הנ"ל השיטות על public static Resistor connect. Series( Resistor[] resistors) { return merge. Array(resistors, new Serial. Resistor. Merger()); } public static Resistor connect. Parallel( Resistor[] resistors) { return merge. Array(resistors, new Parallel. Resistor. Merger()); } 11

: הנ"ל בשיטות המשתמש תוכנית לקטע דוגמה להלן Simple. Resistor[] r 1 = {new Simple. Resistor(2. 0), new Simple. Resistor(6. 0)}; Simple. Resistor[] r 2 = {new Simple. Resistor(3. 0), new Simple. Resistor(1. 0), new Simple. Resistor(2. 0)}; System. out. println(connect. Parallel(r 1). resistance()); System. out. println(connect. Series(r 2). resistance()); : הוא זה קטע של הפלט 1. 5 6. 0 12

Agenda • Stack – http: //docs. oracle. com/javase/6/docs/api/java/util/Stack. html • Queue – http: //docs. oracle. com/javase/6/docs/api/java/util/Queue. html (Interface) • Sources: – nlryan. com/du/cisp 237/ch 17. ppt – http: //www. cis. upenn. edu/~matuszek/cit 594 -2012/Lectures/04 -stacks-queues-deques. ppt – And many others

Stacks and Queues • A stack is a last in, first out (LIFO) data structure – Items are removed from a stack in the reverse order from the way they were inserted • A queue is a first in, first out (FIFO) data structure – Items are removed from a queue in the same order as they were inserted

Array implementation of stacks • To implement a stack, items are inserted and removed at the same end (called the top) • To use an array to implement a stack, you need both the array itself and an integer – The integer tells you either: • Which location is currently the top of the stack, or • How many elements are in the stack 15

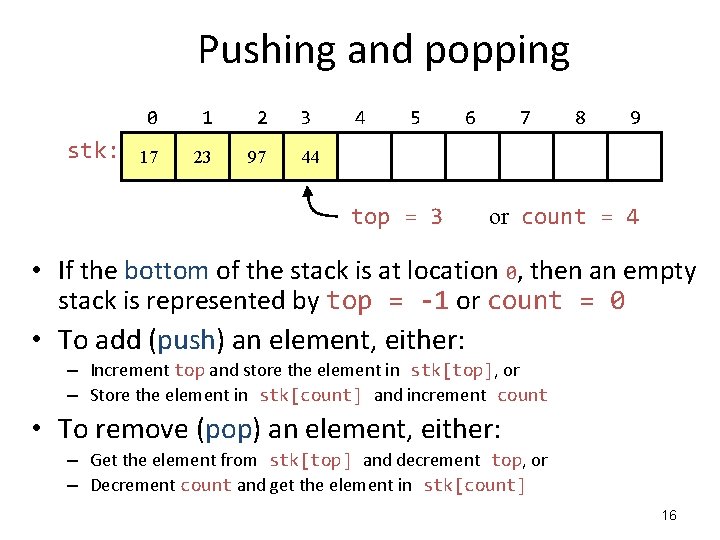
Pushing and popping stk: 0 1 2 17 23 97 3 4 5 6 7 8 9 44 top = 3 or count = 4 • If the bottom of the stack is at location 0, then an empty stack is represented by top = -1 or count = 0 • To add (push) an element, either: – Increment top and store the element in stk[top], or – Store the element in stk[count] and increment count • To remove (pop) an element, either: – Get the element from stk[top] and decrement top, or – Decrement count and get the element in stk[count] 16

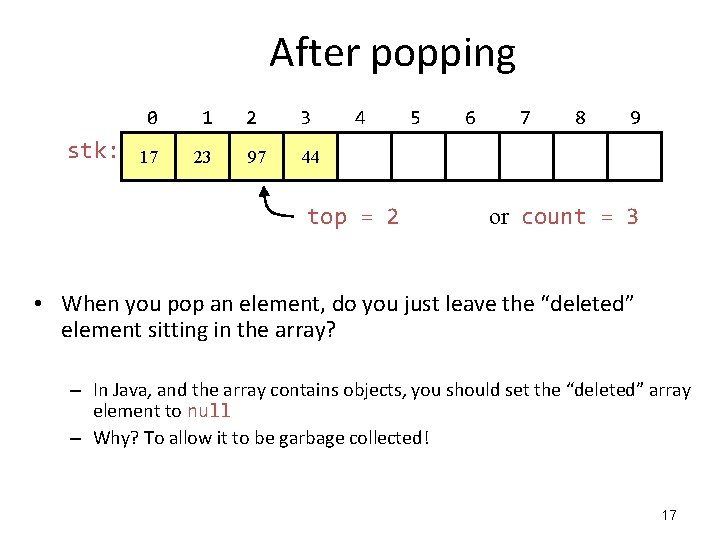
After popping stk: 0 1 17 23 2 3 97 44 4 top = 2 5 6 7 8 9 or count = 3 • When you pop an element, do you just leave the “deleted” element sitting in the array? – In Java, and the array contains objects, you should set the “deleted” array element to null – Why? To allow it to be garbage collected! 17

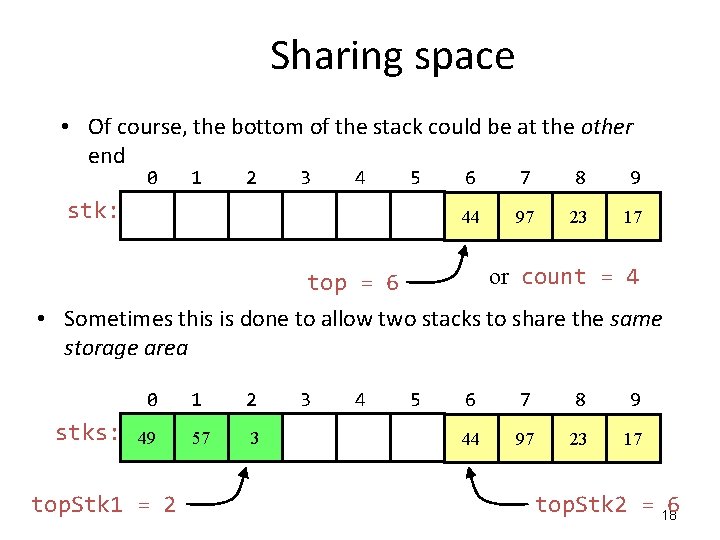
Sharing space • Of course, the bottom of the stack could be at the other end 0 1 2 3 4 5 stk: 6 7 8 9 44 97 23 17 or count = 4 top = 6 • Sometimes this is done to allow two stacks to share the same storage area stks: 0 1 2 49 57 3 top. Stk 1 = 2 3 4 5 6 7 8 9 44 97 23 17 top. Stk 2 = 186

Error checking • There are two stack errors that can occur: – Underflow: trying to pop an empty stack – Overflow: trying to push onto an already full stack • For underflow, you should throw an exception – If you don’t catch it yourself, Java will throw an Array. Index. Out. Of. Bounds exception – You could create your own, more informative exception – We will learn exceptions in week 13 • For overflow, you could do the same things – Or, you could check for the problem, and copy everything into a new, larger array 19

Array implementation of stacks • This implementation is an array of reference variables • Each element of the stack can be assigned to an array slot • The top of the stack is the index of the last element added to the stack • To keep track of the top position, declare a variable called stack. Top 20

Data members private int max. Stack. Size; private int stack. Top; private T[] list; public static final int DEFAULT_SIZE = 100;

Constructors public Stack. Class(int size) { max. Stack. Size = size; stack. Top = 0; list = (T[]) new Object[max. Stack. Size]; } //Default Constructor public Stack. Class() { super(DEFAULT_SIZE); } 22

Push & Pop public void push(T new. Item) { if (is. Full. Stack()) return; list[stack. Top] = new. Item; //add new. Item at the //top of the stack. Top++; //increment stack. Top } public T pop() { if (is. Empty. Stack()) return null; T tmp = (T) list[stack. Top - 1]; //the top item stack. Top--; //decrement stack. Top list[stack. Top] = null; //removing the top item return tmp; //returning the top item 23 }

Other Methods public boolean is. Empty. Stack() { return (stack. Top == 0); } public boolean is. Full. Stack() { return (stack. Top == max. Stack. Size); } 24

Queues s Data structure in which the elements are added at one end, called the rear, and deleted from the other end, called the front s A queue is a First In First Out data structure s As in a stack, the middle elements of the queue are inaccessible 25

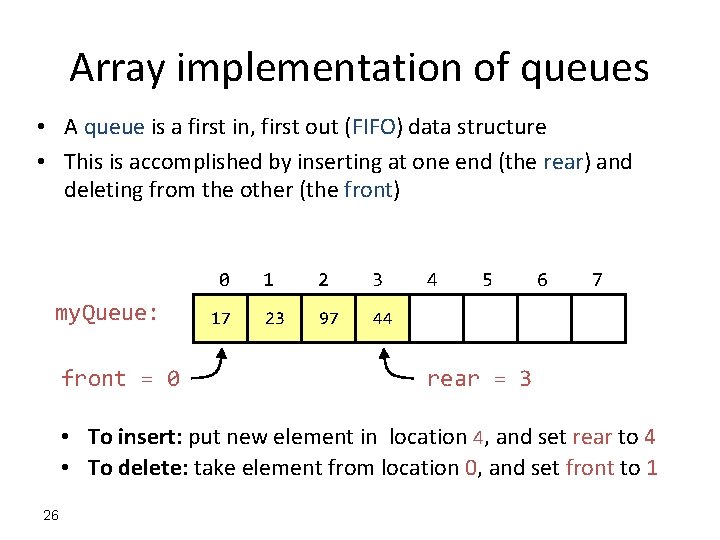
Array implementation of queues • A queue is a first in, first out (FIFO) data structure • This is accomplished by inserting at one end (the rear) and deleting from the other (the front) 0 my. Queue: front = 0 17 1 2 3 23 97 44 4 5 6 7 rear = 3 • To insert: put new element in location 4, and set rear to 4 • To delete: take element from location 0, and set front to 1 26

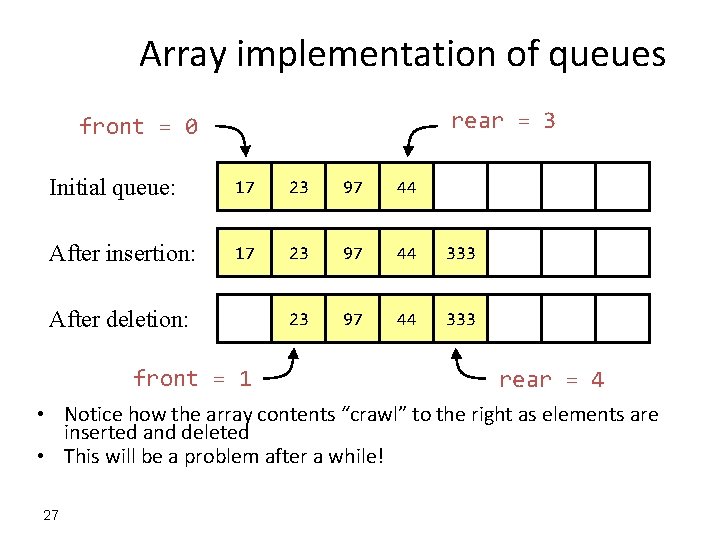
Array implementation of queues rear = 3 front = 0 Initial queue: 17 23 97 44 After insertion: 17 23 97 44 333 After deletion: front = 1 rear = 4 • Notice how the array contents “crawl” to the right as elements are inserted and deleted • This will be a problem after a while! 27

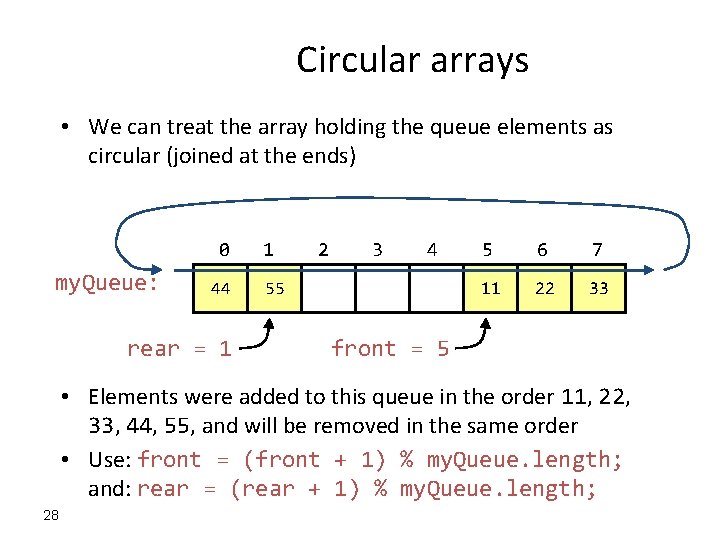
Circular arrays • We can treat the array holding the queue elements as circular (joined at the ends) 0 my. Queue: 44 rear = 1 1 2 3 4 55 5 6 7 11 22 33 front = 5 • Elements were added to this queue in the order 11, 22, 33, 44, 55, and will be removed in the same order • Use: front = (front + 1) % my. Queue. length; and: rear = (rear + 1) % my. Queue. length; 28

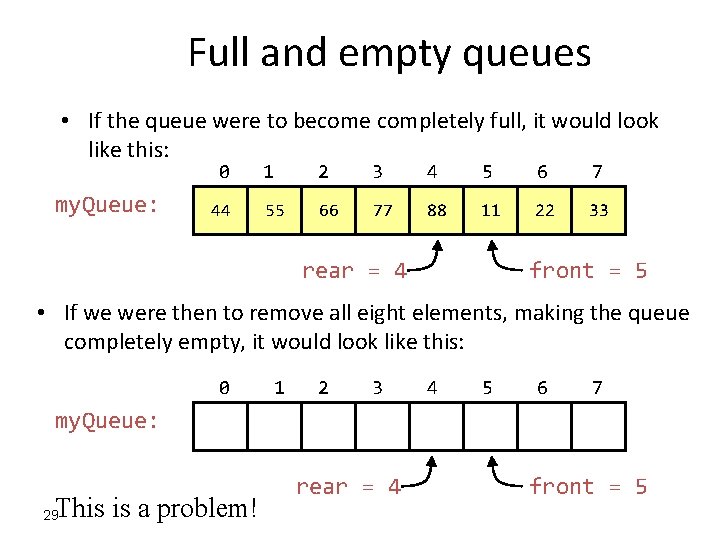
Full and empty queues • If the queue were to become completely full, it would look like this: 0 my. Queue: 44 1 2 3 4 5 6 7 55 66 77 88 11 22 33 rear = 4 front = 5 • If we were then to remove all eight elements, making the queue completely empty, it would look like this: 0 1 2 3 4 5 6 7 my. Queue: This is a problem! 29 rear = 4 front = 5

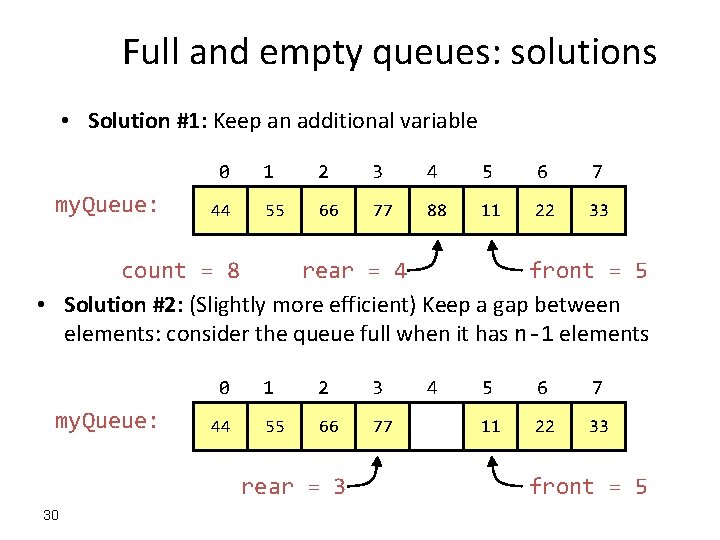
Full and empty queues: solutions • Solution #1: Keep an additional variable 0 my. Queue: 44 1 2 3 4 5 6 7 55 66 77 88 11 22 33 rear = 4 count = 8 front = 5 • Solution #2: (Slightly more efficient) Keep a gap between elements: consider the queue full when it has n-1 elements 0 my. Queue: 44 1 2 3 55 66 77 rear = 3 30 4 5 6 7 11 22 33 front = 5

Implementation of Queues as Arrays s Instance variables s s An array to store the queue elements queue. Front: keeps track of the first element queue. Rear: keeps track of the last element max. Queue. Size: specifies the maximum size of the queues 31

Implementation of Queues as Arrays (continued) s Problems with this implementation s Arrays have fixed sizes s After various insertion and deletion operations, queue. Rear will point to the last array position s Giving the impression that the queue is full s Solutions s Slide all of the queue elements toward the first array position s Use a circular array 32

Data members private int max. Queue. Size; private int queue. Front; private int queue. Rear; private int count; private T[] list; public static final int DEFAULT_SIZE = 100;

Constructors public Queue. Class(int size) { max. Queue. Size = size; queue. Front = 0; //initialize queue. Front queue. Rear = max. Queue. Size - 1; //initialize queue. Rear count = 0; list = (T[]) new Object[max. Queue. Size]; //create the //array to implement the queue } //Default constructor public Queue. Class() { this(DEFAULT_SIZE); } 34

Add & Delete public void add (T queue. Element) { if (is. Full. Queue()) return; //use the mod operator to advance queue. Rear because the array is circular queue. Rear = (queue. Rear + 1) % max. Queue. Size; count++; list[queue. Rear] = queue. Element; } public T remove() { if (is. Empty. Queue()) return null; count--; T tmp = list[queue. Front]; list[queue. Front] = null; //use the mod operator to advance queue. Front because the array is circular queue. Front = (queue. Front + 1) % max. Queue. Size; return tmp; 35 }

Other Methods public boolean is. Empty. Queue() { return (count == 0); } public boolean is. Full. Queue() { return (count == max. Queue. Size); } public T front() { if (is. Empty. Queue()) return null; return list[queue. Front]; } public T back() { if (is. Empty. Queue()) return null; return (T) list[queue. Rear]; } 36

public static boolean check. Palindrom 2(Stack s 1, int num. Of. Elements) int i; int temp. Val=0; Queue q 2=new Queue(); // move all items to q 2 and for (i=1; i<=num. Of. Elements; i++){ temp. Val=s 1. pop (); q 2. enqueue(temp. Val); } // return half of the item to the original stack for (i=1; i<=num. Of. Items/2; i++){ temp. Val=q 2. dequeue(); s 1. push(temp. Val); } //if the number of items is odd: ignore middle item. if ((num. Of. Items % 2) != 0) temp. Val=q 2. dequeue(); // now the q 2 holds half of the items in a reversed //order, and s 1 holds half of the item in their original //order. Compare the items for (i=1; i<=num. Of. Items/2; i++){ { if (s 1. pop()!=q 2. dequeue()) return false; } return true; } {

Finding the smallest difference The naïve way: public static int minimal. Dif(int[] numbers){ int diff = Integer. MAX_VALUE; for(int i=0; i<numbers. length; i++){ for(int j=i+1; j<numbers. length; j++){ int current. Diff = Math. abs(numbers[i]-numbers[j]); if(current. Diff<diff){ diff = current. Diff; } } } return diff; }

Complexity of the naïve case • The internal loop runs n-1 times, then n-2 times, then n-3 times, … • As we’ve seen before , this also gives O(n 2) running time. • A faster idea: Use a sorting algorithm that works in O(n·log(n)), then go over consecutive pairs only. • What is the total running time this way?

Finding the smallest difference The better way: Assumes numbers is ordered in nondecreasing order. public static int minimal. Dif(int[] numbers){ int diff = Integer. MAX_VALUE; for(int i=0; i<numbers. length-1; i++){ int current. Diff = Math. abs(numbers[i]-numbers[i+1]); if(current. Diff<diff){ diff = current. Diff; } } return diff; }

Find Sum x+y=z static boolean Find. Sum(int []data, int z){ for (int i=0; i < data. length; i++){ for (int j=i+1; j<data. length; j++){ if (data[i]+data[j] == z){ System. out. println("x=" + data[i] + " and y=" + data[j]); return true; } } } return false; } How do we show the complexity? 45

Complexity • Remember the analysis for Bubble Sort: – First loop has n iterates. – Inner loop:

Find Sum in sorted array x+y=z static boolean Find. Sum. Sorted(int []data, int z){ int lower=0, upper=data. length-1; while ((data[lower]+data[upper] != z) && (lower < upper)) { if (data[lower]+data[upper] > z) upper--; else if (data[lower]+data[upper] < z) lower++; } if (lower >= upper) { return false; } else { System. out. println("x=" + data[lower] + " and y=" + data[upper]); } return true; } 47 Complexity?

Sample Exam Question • You are given an unsorted array of “Flat” objects, which have a method get. Num( ) that returns a value between 1 and 4 • Sort the array of objects in time O(n), calling get. Num( ) no more than once on each object • Do not create new heap objects 3 1 4 4 2 3 1 1 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9]

Exam Question • This was a moed bet question; many students did a “count-sort”, which they had learned in the second semester • “Run through the array, count how many times each object appears, shift objects around” • This did not satisfy the requirement to call get. Num( ) no more than once on each object • A correct answer is a simple extension of the Dutch Flag problem solution

public static void sort. Flats (Flat[] flats) { int border 1 = -1; int border 2 = 0; int border 3 = flats. length-1; int border 4 = flats. length; do { switch ( flats[border 2]. get. Num( ) ) { case 1: border 1++; swap(flats, border 1, border 2); border 2++; break; case 2: border 2++; break; case 3: swap(flats, border 2, border 3); border 3 --; break; case 4: border 4 --; swap(flats, border 2, border 4); if (border 3 < border 4) swap(flats, border 2, border 3); border 3 --; break; } } while border 2 <= border 3; and write swap( ). . . }

Sample Question 2 • Assume that you have an array, u, of n integers, where no integer appears more than once. u is said to be unimodal if there is some index i (where 0 ≤ i ≤ n-1) such that u[0], …, u[i] is a strictly increasing sequence and u[i], …, u[n-1] is a strictly decreasing sequence. • For example, u = 2, 4, 8, 7, 6, 5, 4, 1, 0, -1 is unimodal, and u = 5, 3, 2, 1 is unimodal, but u = 2, 3, 1, 4 is not.

Sample Question 2 a • Write a non-recursive method that receives an array of integers, returns the value of i if the array is unimodal, and returns -1 if the array is not unimodal. Make this method as efficient as you can. • What are the big-O best-case and worst -case complexities of your method? Explain.

/******************************* * Once a unimodal array starts decreasing, it doesn’t increase * @param data * Possibly unimodal array data[ ] * @return * The location of the array’s single peak, or -1 if the array is not unimodal * Best case: O(1) --- it can discover the first two values are equal * Worst case: O(n) --- it has to run through whole array to check if it's unimodal *******************************/ public static int unimodal. Check (int[ ] data) { int last = data. length - 1, max. Loc = 0; // location of peak boolean falling = false; for (int i = 0; i < last; i++) { if (data[i+1] == data[i]) return -1; if (data[i+1] > data[i]) { if (falling == true) return -1; else max. Loc = i+1; } else falling = true; // data[i] > data[i+1] } return max. Loc; // we get here, it's a unimodal array }

Sample Question 2 b • Now write a non-recursive method that is guaranteed to receive a unimodal array of integers, and returns the value of i. Make this method as efficient as you can. • What are the big-O best-case and worst -case complexities of your method? Explain.

/******************************* * A unimodal binary search, checking for a complete peak at each jump. * There are no duplicated contiguous entries in the array, by the definition of * unimodal arrays --- and the array is guaranteed unimodal, we're just * looking for the peak * @param data * Guaranteed unimodal array data[ ] * @return * The location of the array’s single peak * Best case: O(1) --- might find peak after first calculation of middle * Worst case: O(log n) --- it might have to collapse the unknown region to a * single array location, before it finds the peak; but the collapsing is done * like binary search, so it cuts the unknown region in half each time *******************************/

public static int unimodal (int[ ] data) { int middle, lower = 0, upper = (data. length - 1); do { middle = ((lower + upper) / 2); if (middle == 0) { if (upper == 0) return 0; // array of one element else if (data[middle] > data[middle+1]) return middle; else return (middle+1); } else { if (data[middle] > data[middle+1]) { if (data[middle] > data[middle-1]) return middle; else upper = middle-1; } else lower = middle+1; } } while (lower < upper); // we stop if lower and upper meet // if we get here, data[lower] is the array’s peak return lower; } // unimodal