TimingDriven Routing for FPGAs Based on Lagrangian Relaxation

Timing-Driven Routing for FPGAs Based on Lagrangian Relaxation Seokjin Lee*, D. F. Wong+ *Dept. of Electrical and Computer Engineering +Dept. of Computer Sciences The University of Texas at Austin 1

Outline n n Overview Introduction n Problem Formulation n n Routing graphs and Timing graphs Algorithm Description n n FPGA Architecture, Routing resources FPGA routing problem Lagrangian Relaxation LR_ROUTE, NET_ROUTE Experimental Results Conclusion 2

Overview n n A new timing-driven routing algorithm for FPGAs Find a routing with minimum critical path delay for a given placed circuit. Handling of the timing constraints in a mathematical programming framework. Routing results are compared with those of VPR router. 3

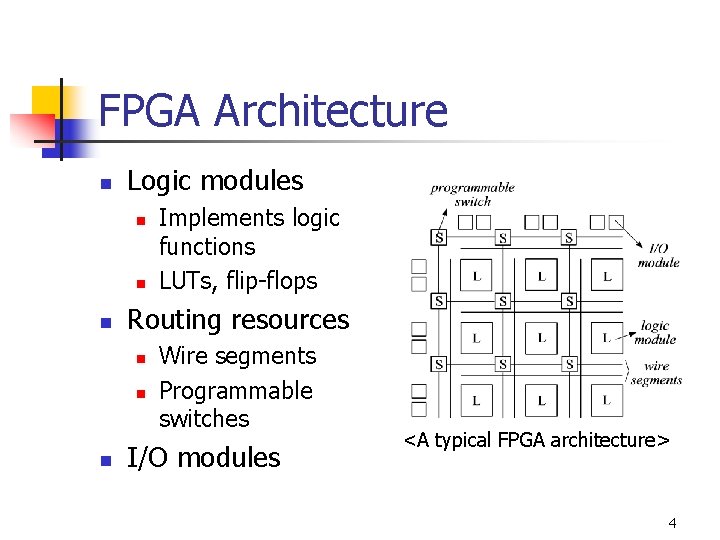
FPGA Architecture n Logic modules n n n Routing resources n n n Implements logic functions LUTs, flip-flops Wire segments Programmable switches I/O modules <A typical FPGA architecture> 4

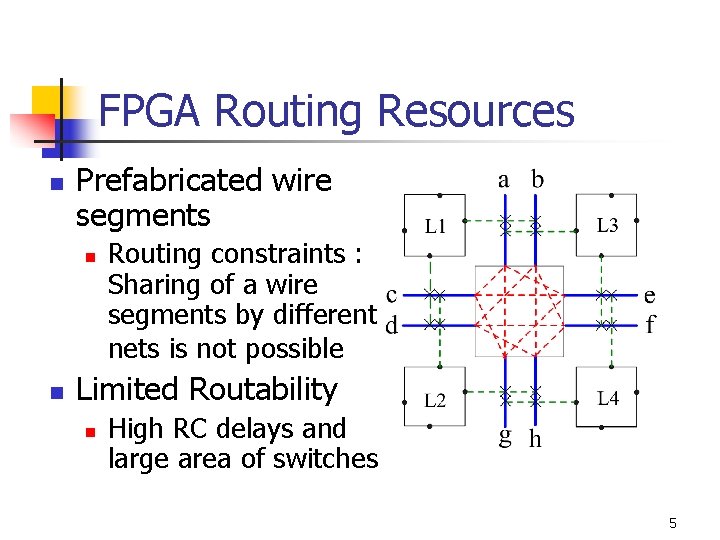
FPGA Routing Resources n Prefabricated wire segments n n Routing constraints : Sharing of a wire segments by different nets is not possible Limited Routability n High RC delays and large area of switches 5

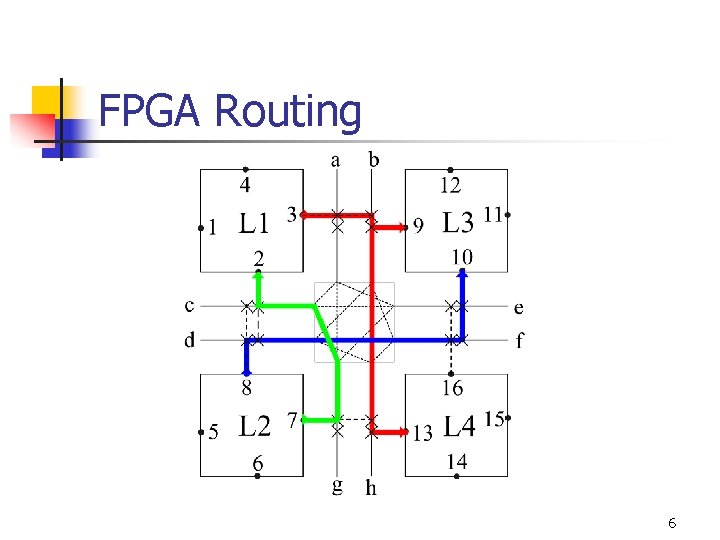
FPGA Routing 6

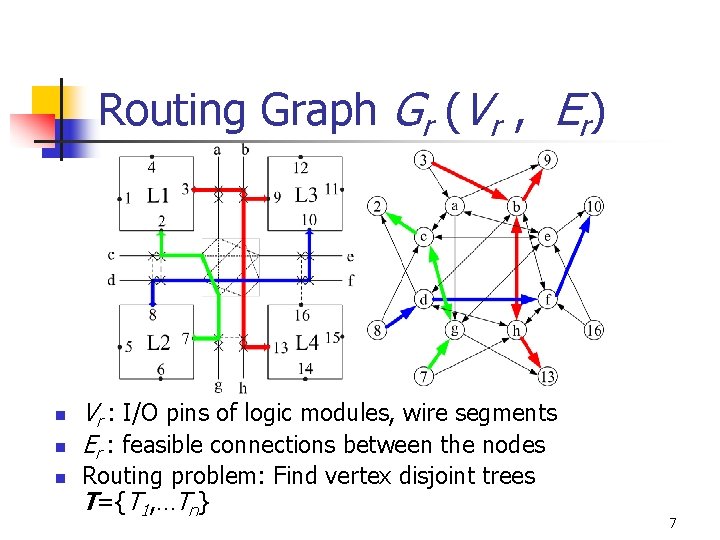
Routing Graph Gr (Vr , Er) n n n Vr : I/O pins of logic modules, wire segments Er : feasible connections between the nodes Routing problem: Find vertex disjoint trees T={T 1, …Tn} 7

Timing Constraints n Source-to-sink delays of nets n n n Delay of wire-switch chains Calculated from architecture specific RC values based on Elmore delay model Timing constraints n Specified by arrival times at primary inputs (outputs of storage elements) or required times at primary outputs (inputs of storage elements) 8

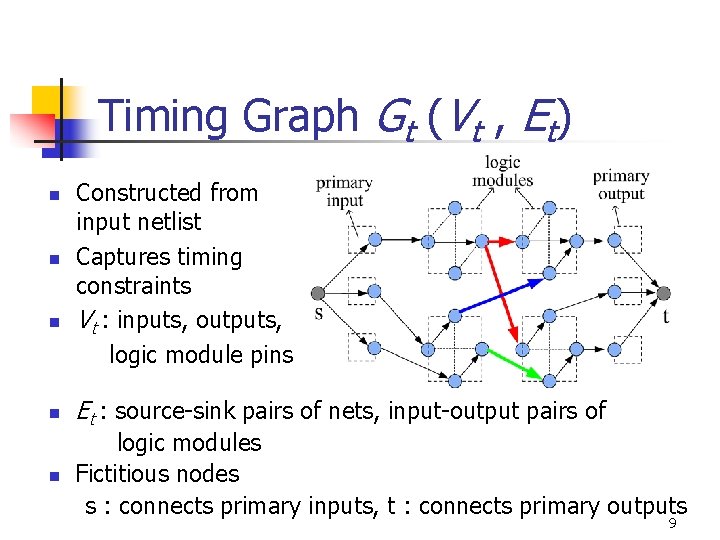
Timing Graph Gt (Vt , Et) n n n Constructed from input netlist Captures timing constraints Vt : inputs, outputs, logic module pins Et : source-sink pairs of nets, input-output pairs of logic modules Fictitious nodes s : connects primary inputs, t : connects primary outputs 9

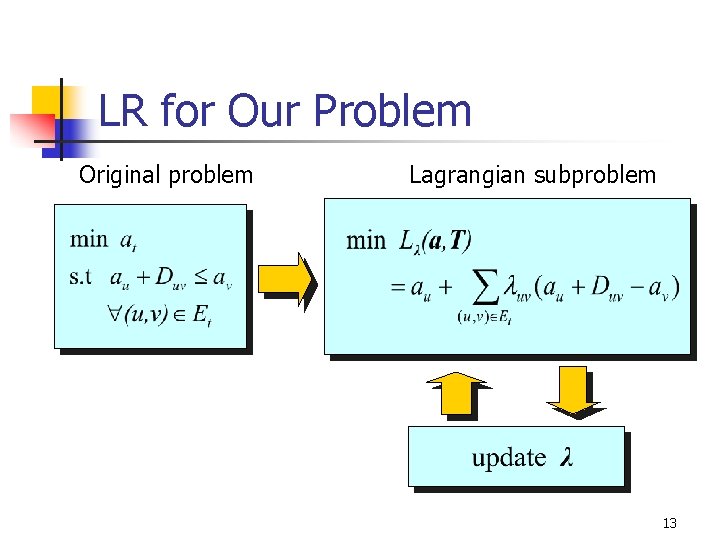
Timing-Driven FPGA Routing n n Minimization of critical path delay under timing and routing constraints Find vertex disjoint routing trees T = {T 1, …, Tn} for all the nets such that Minimize subject to 10

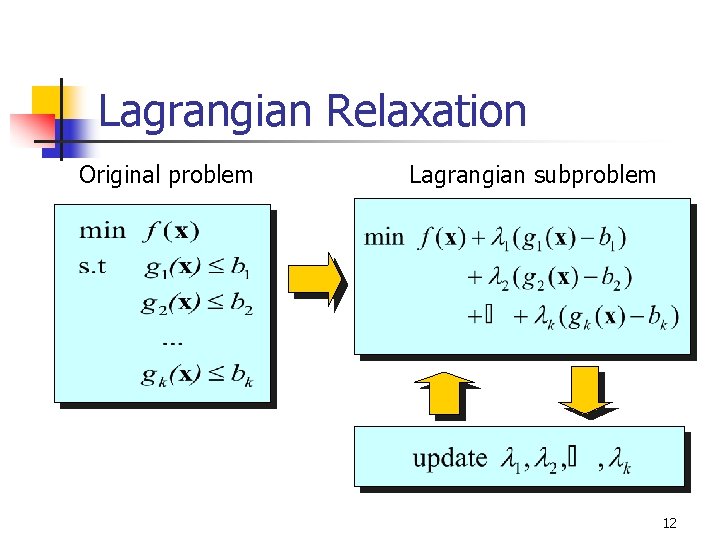
Lagrangian Relaxation n n General technique for solving optimization problems with difficult constraints Lagrangian subproblems n n New objective function: adding constraints to the original objective function after multiplied by constants (Lagrangian multipliers) Iteratively update Lagrangian multipliers and solve Lagrangian subproblems 11

Lagrangian Relaxation Original problem Lagrangian subproblem 12

LR for Our Problem Original problem Lagrangian subproblem 13

Optimality Conditions n n Optimality conditions on By rearranging terms, 14

Simplified Lagrangian Subproblem Optimality conditions on Lagrangian subproblem becomes 15

Updating Lagrangian Multipliers Subgradient Method : stepsize 16

LR_ROUTE 1. 2. 3. 4. 5. Initialize Call NET_ROUTE to solve LS( ) Compute for each Update for each Repeat Steps 2 -4 until no shared resource exists. 17

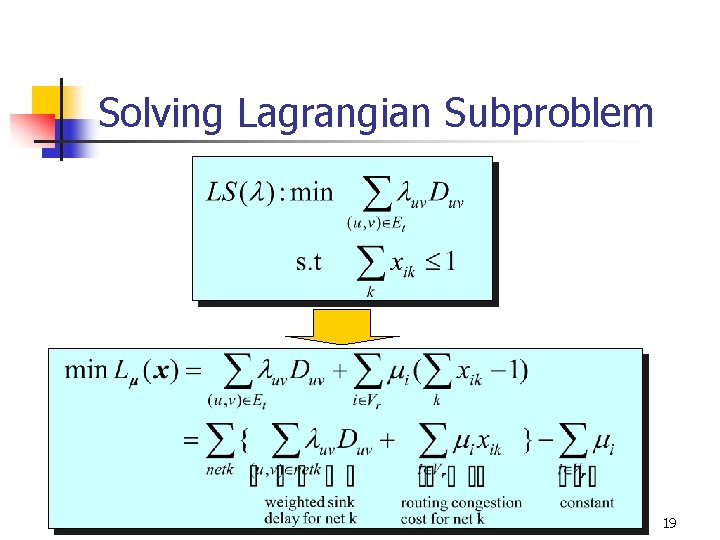
Solving Lagrangian Subproblem n n NET_ROUTE Find routing trees T for a set of given multipliers such that Minimize subject to where 18

Solving Lagrangian Subproblem 19

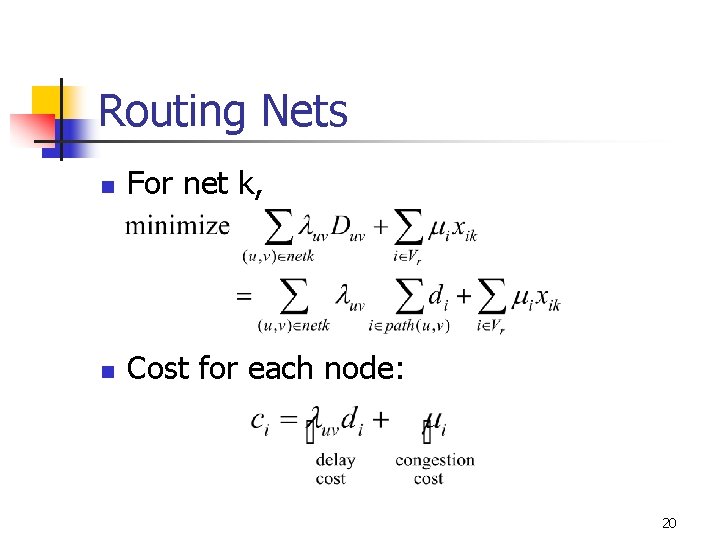
Routing Nets n For net k, n Cost for each node: 20

NET_ROUTE 1. 2. 3. 4. 5. For each net k Rip up routing for net k for each sink v of net k Maze route from source to sink with cost Update for all nodes in 21

Experimental Results n FPGA model used n n n Symmetrical-array-based FPGA Each logic block contains four 4 -input LUTs and flipflops Switch connections: Fs = 3, Fc = W Fs: number of connections per wire entering the switch box Fc : number of tracks to which each logic block pin can connect W : number of tracks in a channel 22

Experimental Results n n Tested on large circuits from MCNC benchmark Routing with fixed channel width n n n Minimum channel width obtained by running VPR in timing-driven mode Better results for 13 circuits (out of 17) Critical path delay improved up to 33% with comparable runtime 23

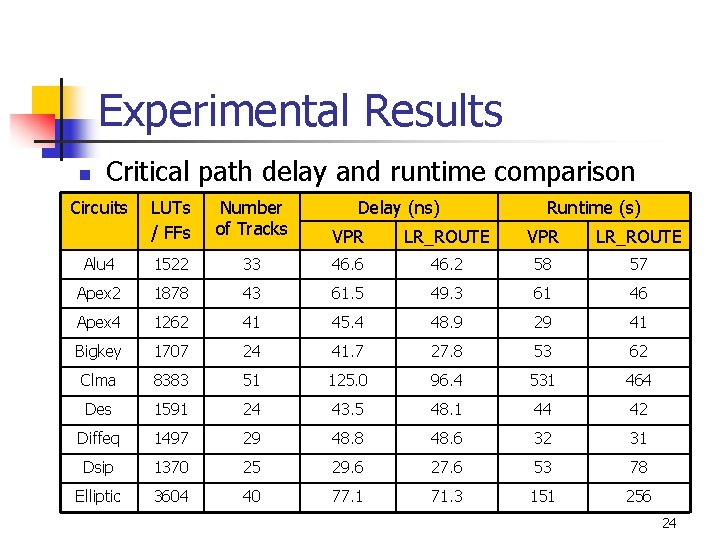
Experimental Results n Critical path delay and runtime comparison Circuits LUTs / FFs Number of Tracks Delay (ns) Runtime (s) VPR LR_ROUTE Alu 4 1522 33 46. 6 46. 2 58 57 Apex 2 1878 43 61. 5 49. 3 61 46 Apex 4 1262 41 45. 4 48. 9 29 41 Bigkey 1707 24 41. 7 27. 8 53 62 Clma 8383 51 125. 0 96. 4 531 464 Des 1591 24 43. 5 48. 1 44 42 Diffeq 1497 29 48. 8 48. 6 32 31 Dsip 1370 25 29. 6 27. 6 53 78 Elliptic 3604 40 77. 1 71. 3 151 256 24

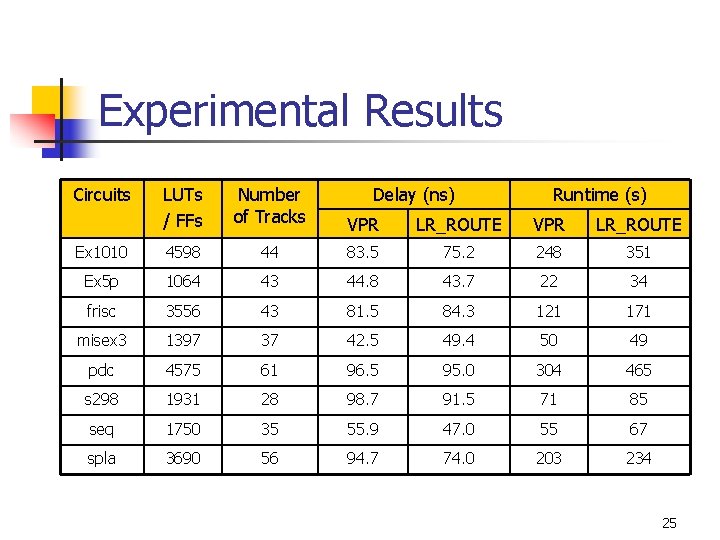
Experimental Results Circuits LUTs / FFs Number of Tracks Delay (ns) Runtime (s) VPR LR_ROUTE Ex 1010 4598 44 83. 5 75. 2 248 351 Ex 5 p 1064 43 44. 8 43. 7 22 34 frisc 3556 43 81. 5 84. 3 121 171 misex 3 1397 37 42. 5 49. 4 50 49 pdc 4575 61 96. 5 95. 0 304 465 s 298 1931 28 98. 7 91. 5 71 85 seq 1750 35 55. 9 47. 0 55 67 spla 3690 56 94. 7 74. 0 203 234 25

Conclusion n n A new timing-driven routing algorithm for FPGAs Find a routing with minimum critical path delay for a given placed circuit. Handling of the timing constraints by Lagrangian relaxation. Routing results are better than those of VPR router. 26