Timing Analysis Section 2 4 2 Delay Time

Timing Analysis Section 2. 4. 2

Delay Time Def: Time required for output signal Y to change due to change in input signal X t=0 Up to now, we have assumed this delay time has been 0 seconds.

Delay Time In a “real” circuit, it will take tp seconds for Y to change due to X t=0 t=tp tp is known as the propagation delay time

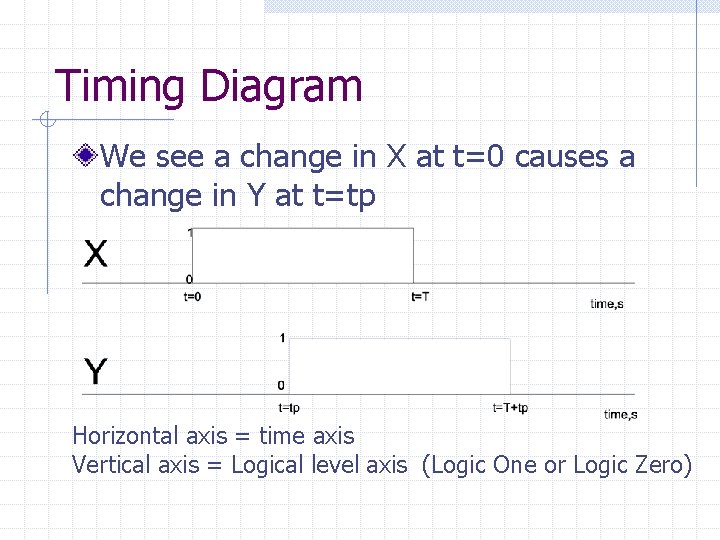
Timing Diagram We use a timing diagram to graphically represent this delay Horizontal axis = time axis Vertical axis = Logical level axis (Logic One or Logic Zero)

Timing Diagram We see a change in X at t=0 causes a change in Y at t=tp Horizontal axis = time axis Vertical axis = Logical level axis (Logic One or Logic Zero)

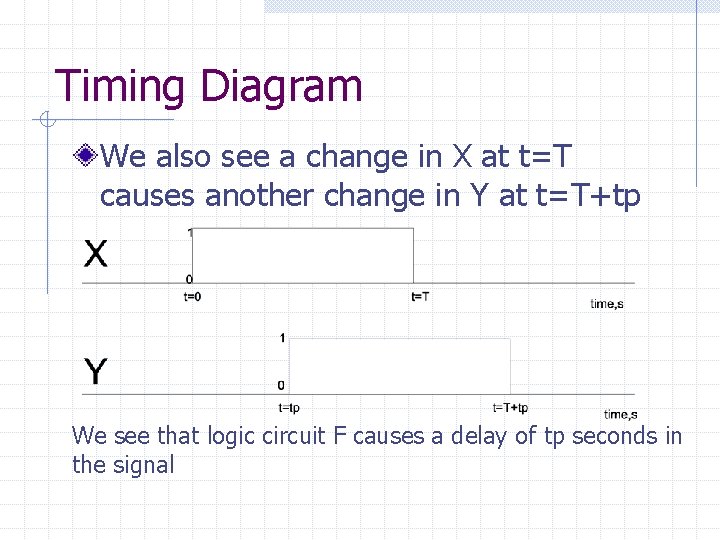
Timing Diagram We also see a change in X at t=T causes another change in Y at t=T+tp We see that logic circuit F causes a delay of tp seconds in the signal

Simple Example – Not Gate Let tp=2 ns Where ns = nanosecond = 1 x 10 -9 seconds 2 ns

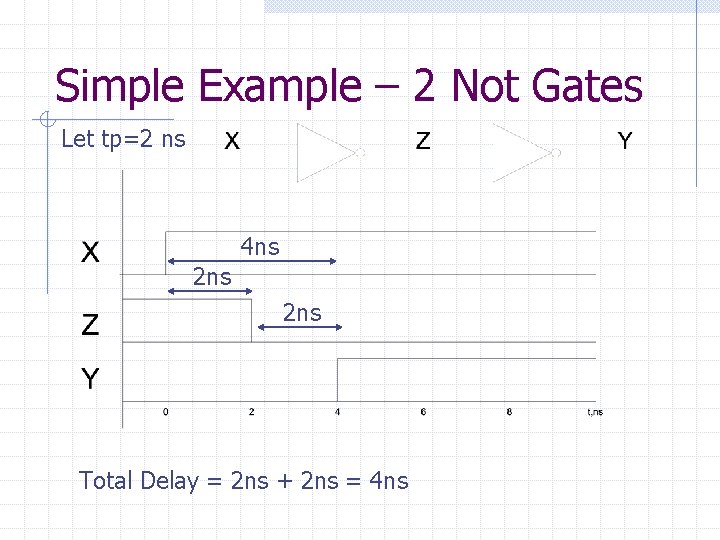
Simple Example – 2 Not Gates Let tp=2 ns 4 ns 2 ns Total Delay = 2 ns + 2 ns = 4 ns

Simple Example – 2 Not Gates Notes: Time axis is shared among signals Logic levels (1 or 0) are implied, not shown

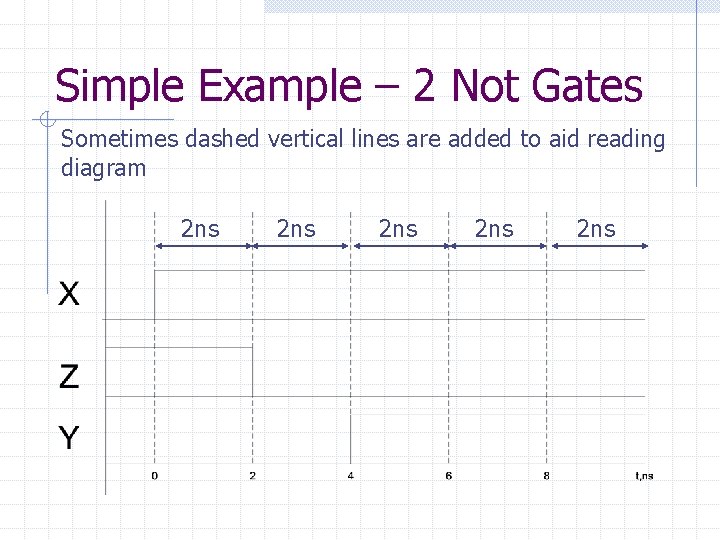
Simple Example – 2 Not Gates Sometimes dashed vertical lines are added to aid reading diagram 2 ns 2 ns 2 ns

Where does this delay come from? Circuit Delay

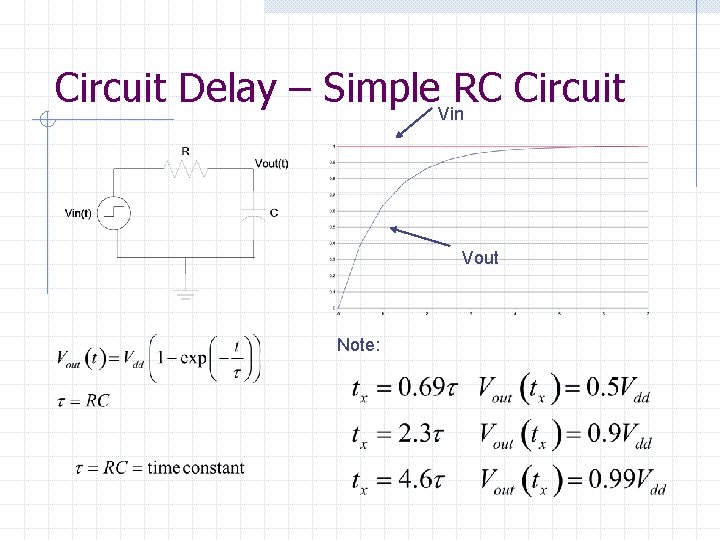
Circuit Delay All electrical circuits have intrinsic resistance (R) and capacitance (C). Let’s analyze a simple RC circuit

Circuit Delay – Simple. Vin. RC Circuit Vout Note:

Circuit Delay – Example Vin Vout Let R=1 ohm, C=1 F, so that RC=1 second Time Delay is 0. 7 s or 700 ms for 0. 5 Vdd Time Delay is 2. 3 s for 0. 9 Vdd Time Delay is 4. 6 s for 0. 99 Vdd

How do we relate this to logic diagrams?

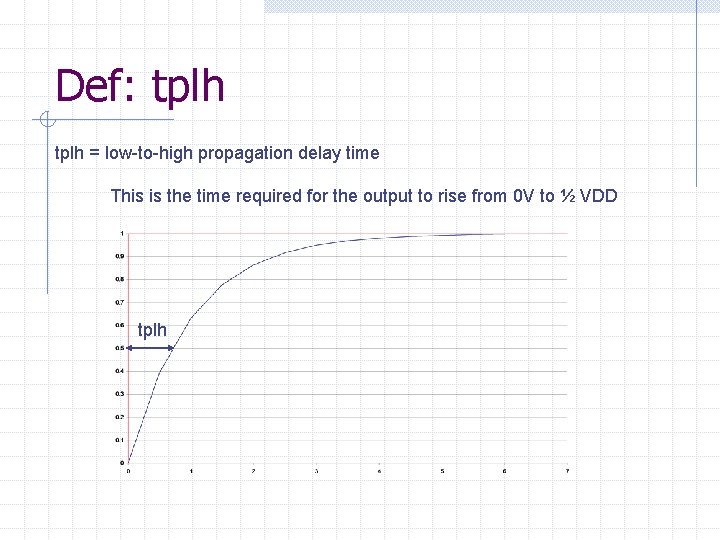
Def: tplh = low-to-high propagation delay time This is the time required for the output to rise from 0 V to ½ VDD tplh

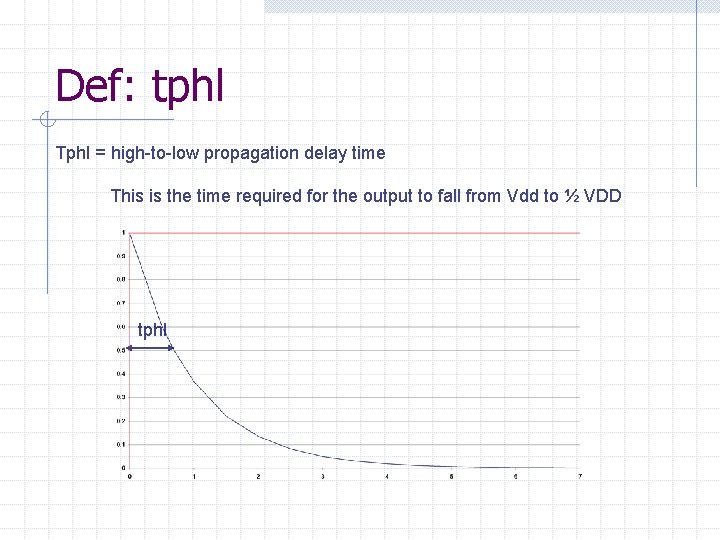
Def: tphl Tphl = high-to-low propagation delay time This is the time required for the output to fall from Vdd to ½ VDD tphl

Def: tp (propagation delay time) Let’s define tp = propagation delay time as This will be the “average” delay through the circuit

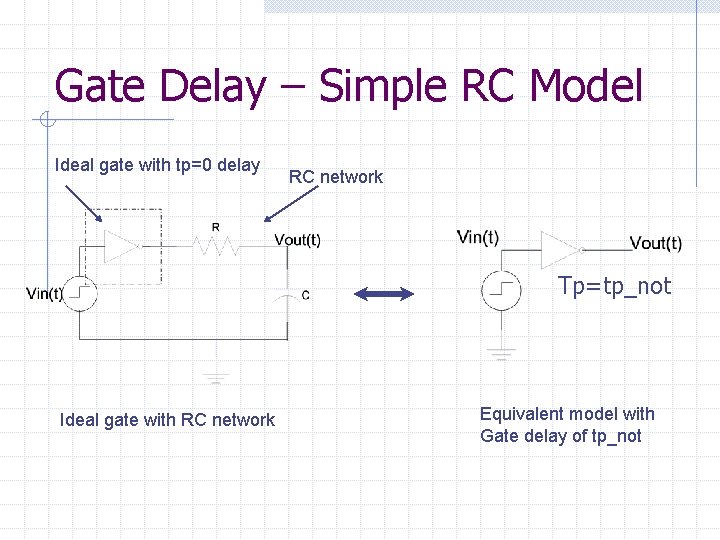
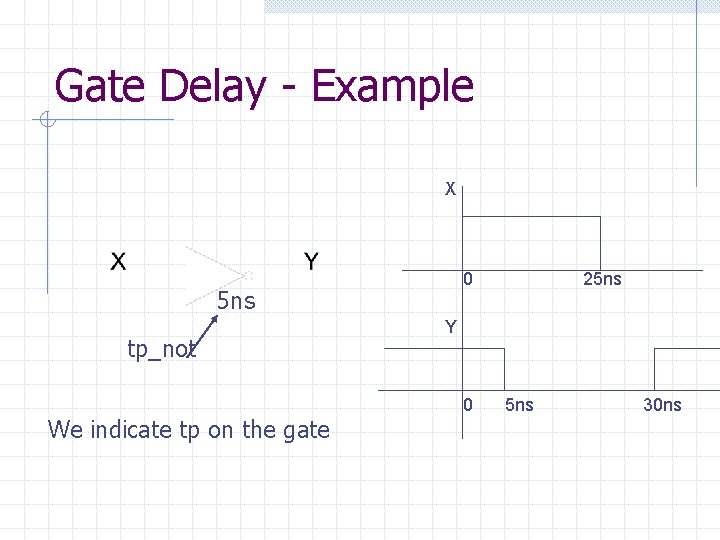
Gate Delay – Simple RC Model Ideal gate with tp=0 delay RC network Tp=tp_not Ideal gate with RC network Equivalent model with Gate delay of tp_not

Gate Delay - Example X 0 5 ns tp_not We indicate tp on the gate 25 ns Y 0 5 ns 30 ns

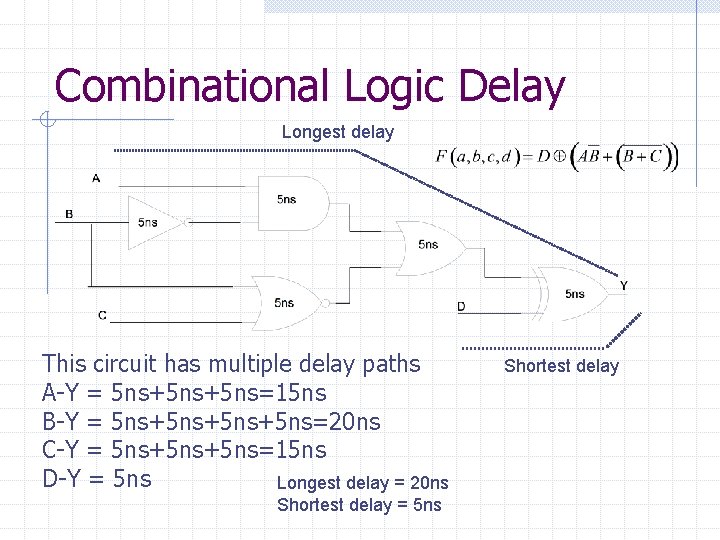
Combinational Logic Delay Longest delay This circuit has multiple delay paths A-Y = 5 ns+5 ns=15 ns B-Y = 5 ns+5 ns+5 ns=20 ns C-Y = 5 ns+5 ns=15 ns D-Y = 5 ns Longest delay = 20 ns Shortest delay = 5 ns Shortest delay

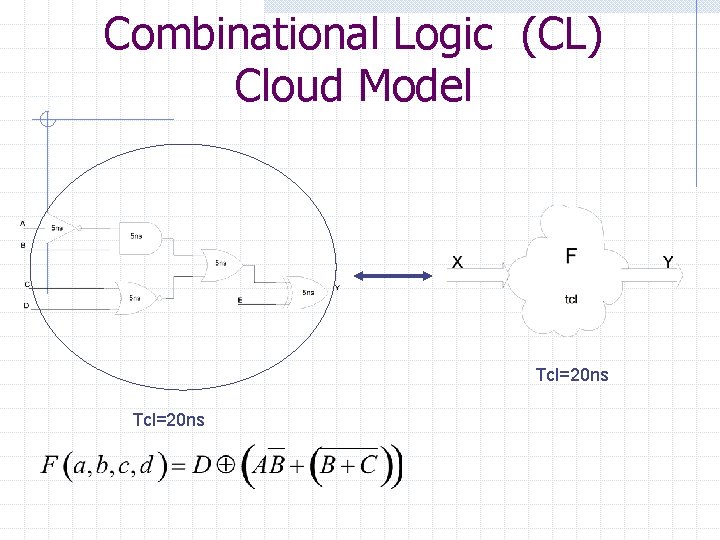
Combinational Logic Delay Longest delay We’ll use the longest delay to represent the logic function F. Let’s call it Tcl for time, combinational logic Longest delay = 20 ns Shortest delay

Combinational Logic (CL) Cloud Model Tcl=20 ns

Logic Simulators Used to simulate the output response of a logic circuit.

Logic Simulations Three primary types n Circuit simulator (e. g. PSPICE) w “Exact” delay for each gate w Most accurate timing analysis w Very slow compared to other types n Functional Simulation (e. g. Quartus ) w Assumes one unit delay for each gate w Very fast compared to other types w Most inaccurate timing analysis n Timing Simulation (e. g. Quartus) w Assumes “average” tp delay for each gate w Not the fastest or slowest timing analysis w Provides “pretty good” timing analysis

TPS Quizzes

Timing Quiz 1

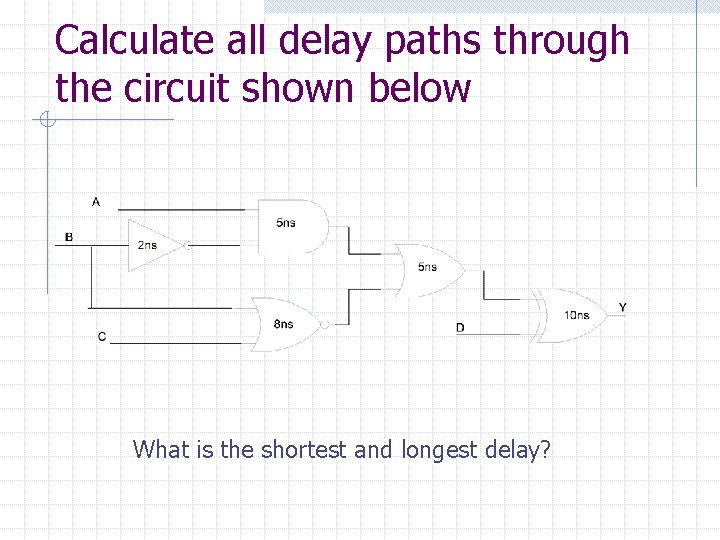
Calculate all delay paths through the circuit shown below What is the shortest and longest delay?

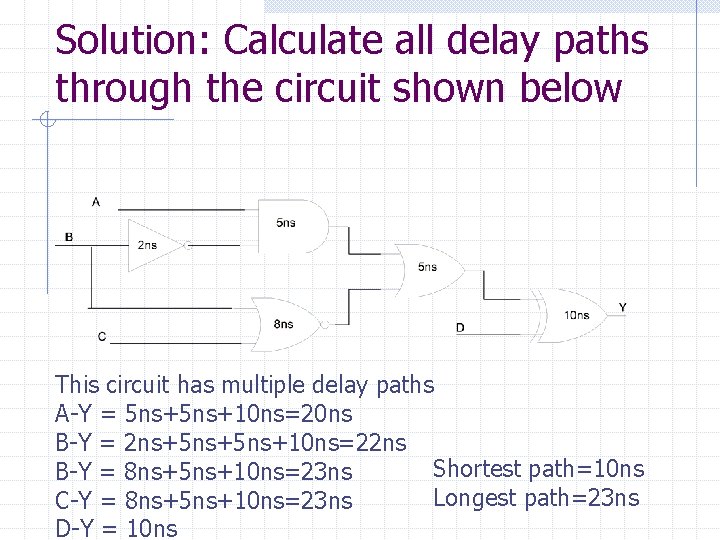
Solution: Calculate all delay paths through the circuit shown below This circuit has multiple delay paths A-Y = 5 ns+10 ns=20 ns B-Y = 2 ns+5 ns+10 ns=22 ns Shortest path=10 ns B-Y = 8 ns+5 ns+10 ns=23 ns Longest path=23 ns C-Y = 8 ns+5 ns+10 ns=23 ns D-Y = 10 ns

Timing Quiz 2

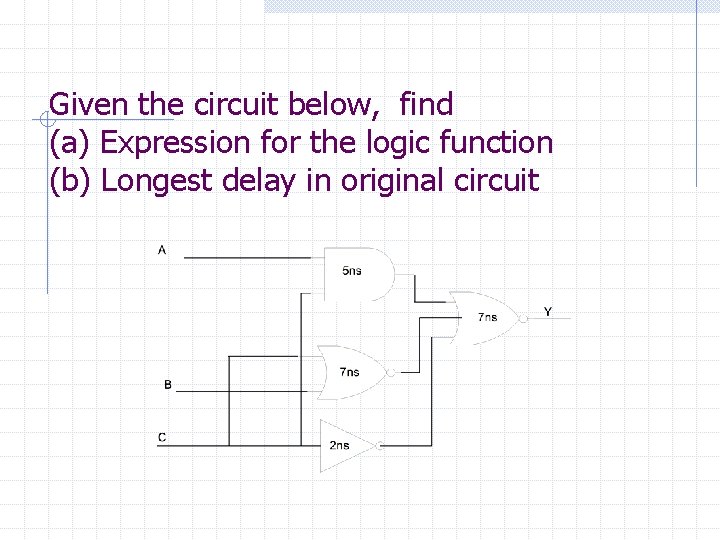
Given the circuit below, find (a) Expression for the logic function (b) Longest delay in original circuit

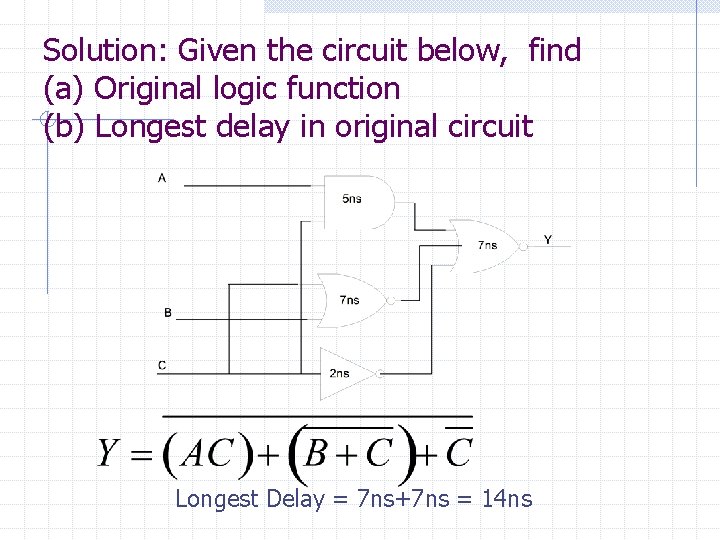
Solution: Given the circuit below, find (a) Original logic function (b) Longest delay in original circuit Longest Delay = 7 ns+7 ns = 14 ns

Timing Quiz 3

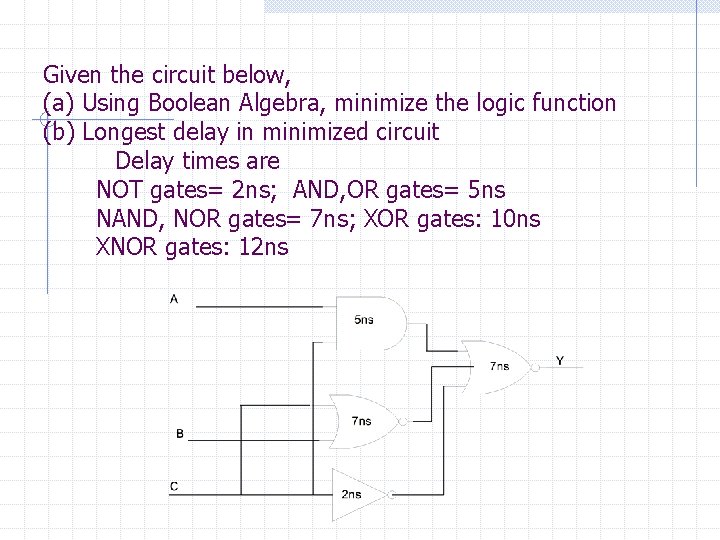
Given the circuit below, (a) Using Boolean Algebra, minimize the logic function (b) Longest delay in minimized circuit Delay times are NOT gates= 2 ns; AND, OR gates= 5 ns NAND, NOR gates= 7 ns; XOR gates: 10 ns XNOR gates: 12 ns

Solution: Given the circuit below, find (a) Minimized logic function (b) Longest delay in minimized circuit Delay times are NOT gates= 2 ns; AND, OR gates= 5 ns NAND, NOR gates= 7 ns; XOR gates: 10 ns XNOR gates: 12 ns You can show

Solution: Given the circuit below, find (a) Minimized logic function (b) Longest delay in minimized circuit Delay times are NOT gates= 2 ns; AND, OR gates= 5 ns NAND, NOR gates= 7 ns; XOR gates: 10 ns XNOR gates: 12 ns Longest delay is 7 ns

Solution Expanded

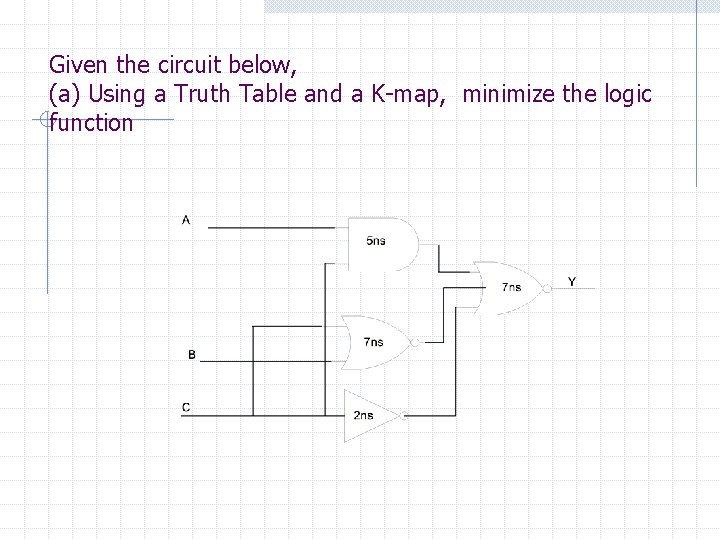
Given the circuit below, (a) Using a Truth Table and a K-map, minimize the logic function

Solution Do yourself!