Timing Analysis of Cyclic Combinational Circuits Marc D

Timing Analysis of Cyclic Combinational Circuits Marc D. Riedel and Jehoshua Bruck California Institute of Technology Marrella splendens Cyclic circuit IWLS, Temecula Creek, CA, June 4, 2004

Combinational Circuits The current outputs depend only on the current inputs outputs combinational logic

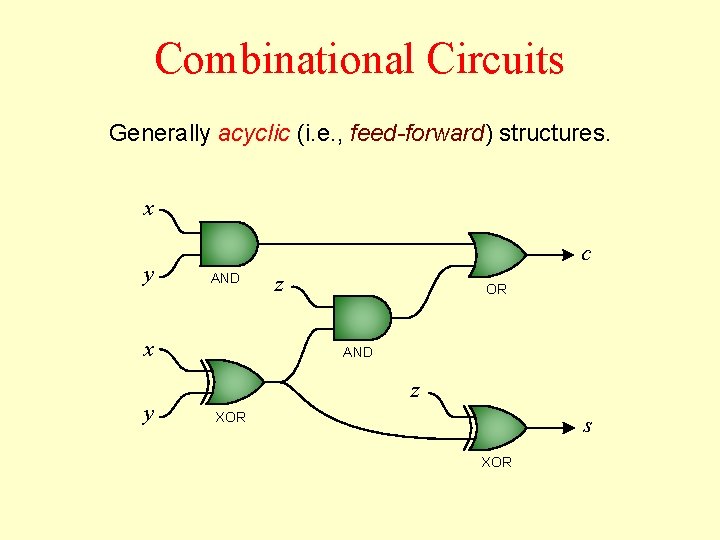
Combinational Circuits Generally acyclic (i. e. , feed-forward) structures. x y c AND x y z OR AND z XOR s XOR

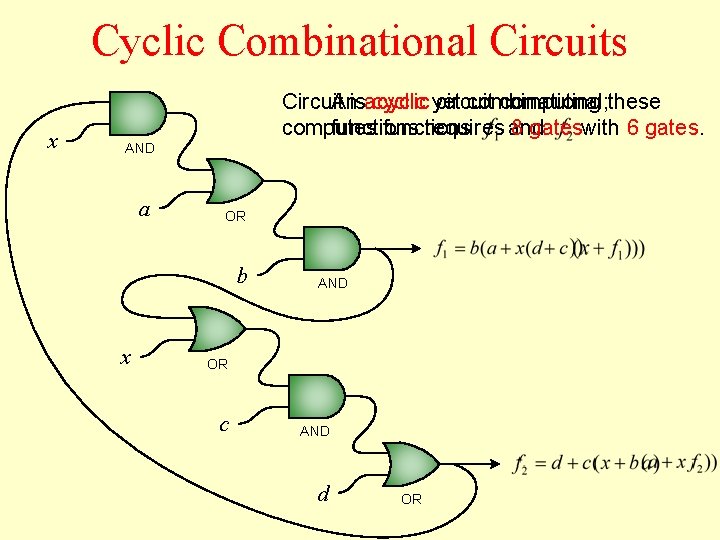
Cyclic Combinational Circuits x Circuit cyclic yet combinational; Anisacyclic circuit computing these computes functions requires and 8 gates. with 6 gates. AND a OR b x AND OR c AND d OR

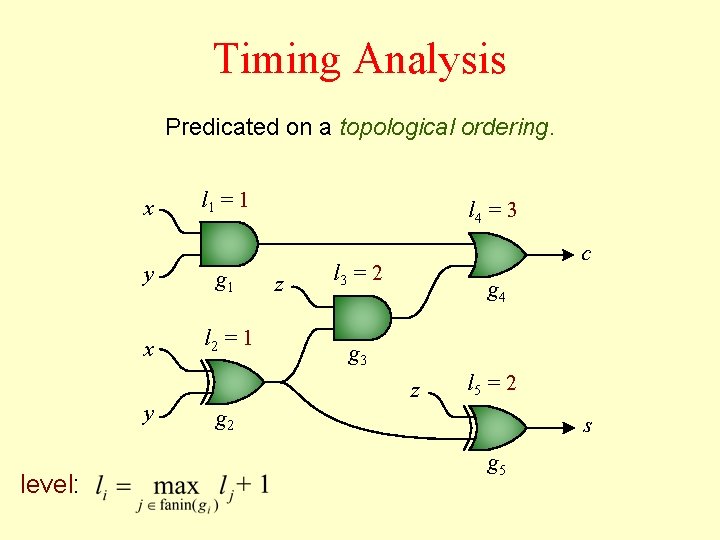
Timing Analysis Predicated on a topological ordering. x y g 1 x l 2 = 1 y level: l 1 = 1 l 4 = 3 z c l 3 = 2 g 4 g 3 z l 5 = 2 g 2 s g 5

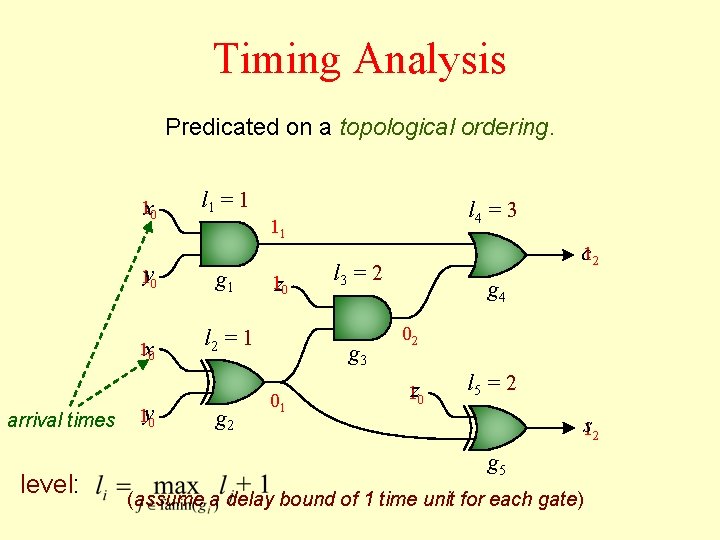
Timing Analysis Predicated on a topological ordering. 1 x 0 1 y 0 1 x 0 arrival times level: 1 y 0 l 1 = 1 l 4 = 3 11 g 1 1 z 0 l 2 = 1 g 2 l 3 = 2 g 3 01 c 12 g 4 02 1 z 0 l 5 = 2 s 12 g 5 (assume a delay bound of 1 time unit for each gate)

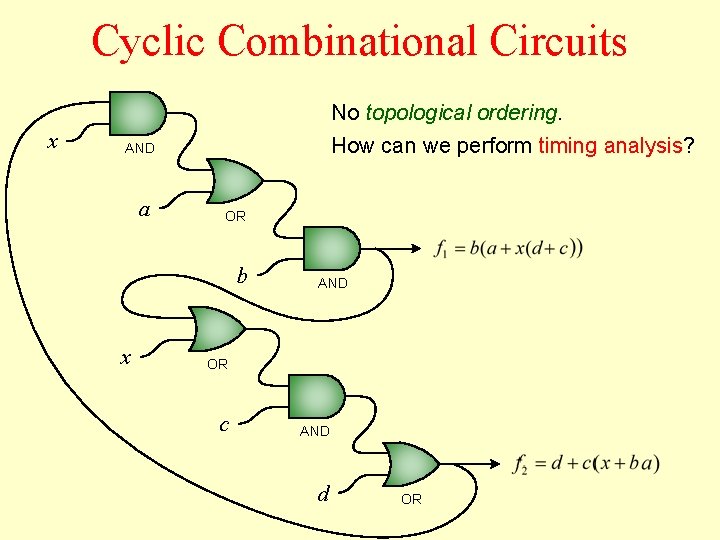
Cyclic Combinational Circuits No topological ordering. x How can we perform timing analysis? AND a OR b x AND OR c AND d OR

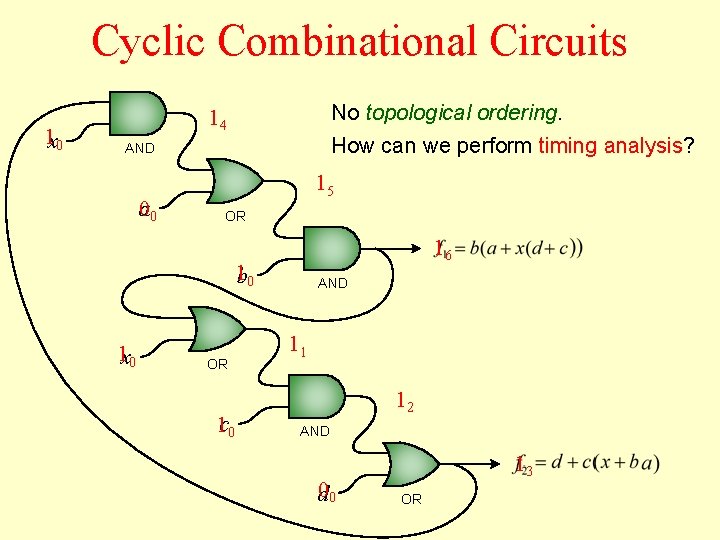
Cyclic Combinational Circuits 1 x 0 No topological ordering. 14 How can we perform timing analysis? AND a 00 15 OR 16 1 b 0 1 x 0 OR 1 c 0 AND 11 12 AND 0 d 0 13 OR

Prior Work In previous papers, we presented: • Algorithms for functional analysis (IWLS’ 03); • Strategies for synthesis (DAC’ 03). In trials on benchmark circuits, cyclic optimizations reduced the area of by as much as 30%

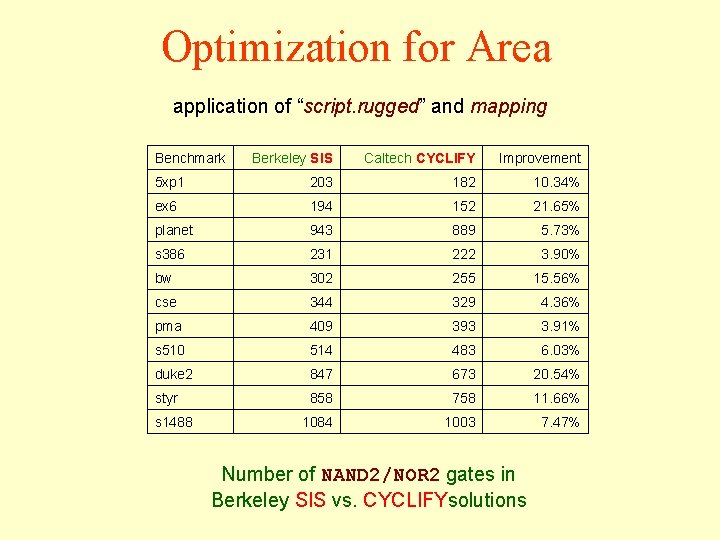
Optimization for Area application of “script. rugged” and mapping Benchmark Berkeley SIS Caltech CYCLIFY Improvement 5 xp 1 203 182 10. 34% ex 6 194 152 21. 65% planet 943 889 5. 73% s 386 231 222 3. 90% bw 302 255 15. 56% cse 344 329 4. 36% pma 409 393 3. 91% s 510 514 483 6. 03% duke 2 847 673 20. 54% styr 858 758 11. 66% 1084 1003 7. 47% s 1488 Number of NAND 2/NOR 2 gates in Berkeley SIS vs. CYCLIFYsolutions

Contributions In this paper, we discuss: • An algorithm for timing analysis. • Synthesis results, with optimization jointly targeting area and delay. In trials on benchmarks circuits, cyclic optimizations simultaneously reduced the area by up to 10% and the delay by up to 25%.

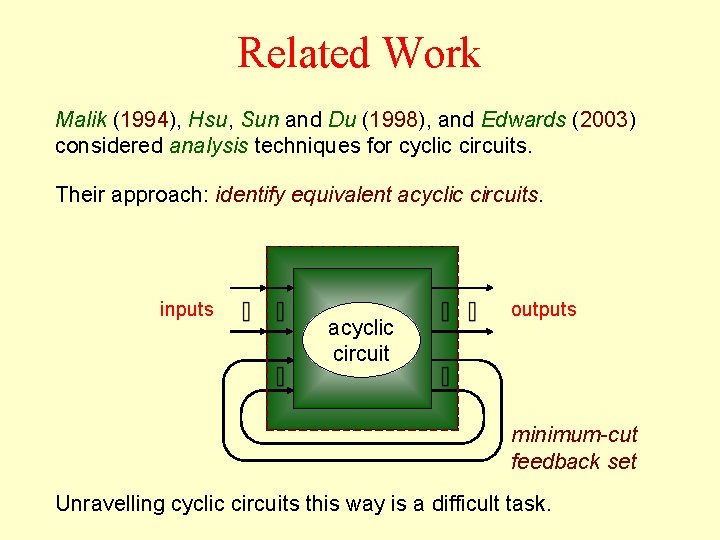
Related Work Malik (1994), Hsu, Sun and Du (1998), and Edwards (2003) considered analysis techniques for cyclic circuits. Their approach: identify equivalent acyclic circuits. inputs acyclic circuit outputs minimum-cut feedback set Unravelling cyclic circuits this way is a difficult task.

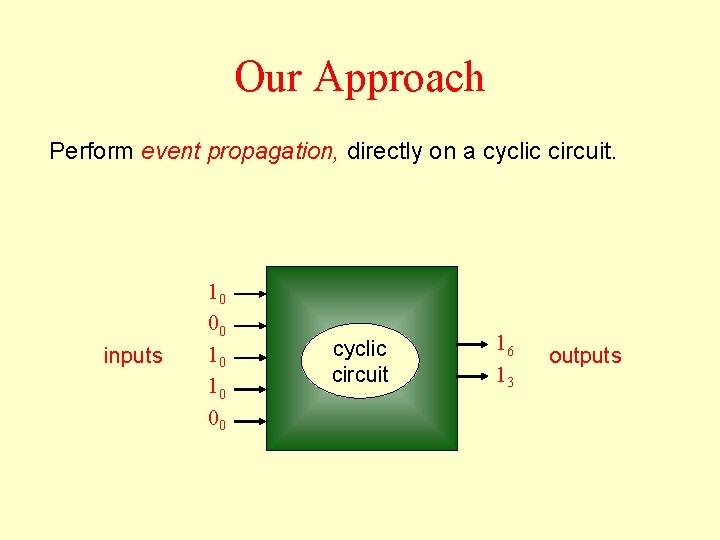
Our Approach Perform event propagation, directly on a cyclic circuit. inputs 10 00 10 10 00 cyclic circuit 16 13 outputs

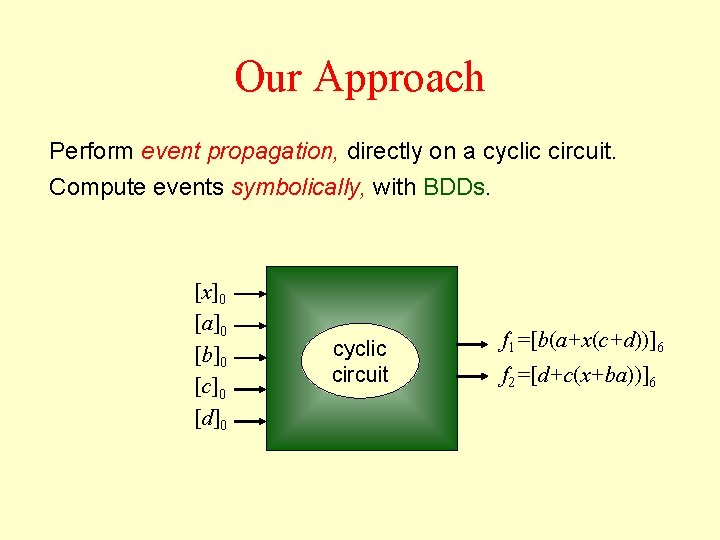
Our Approach Perform event propagation, directly on a cyclic circuit. Compute events symbolically, with BDDs. [x]0 [a]0 [b]0 [c]0 [d]0 cyclic circuit f 1=[b(a+x(c+d))]6 f 2=[d+c(x+ba))]6

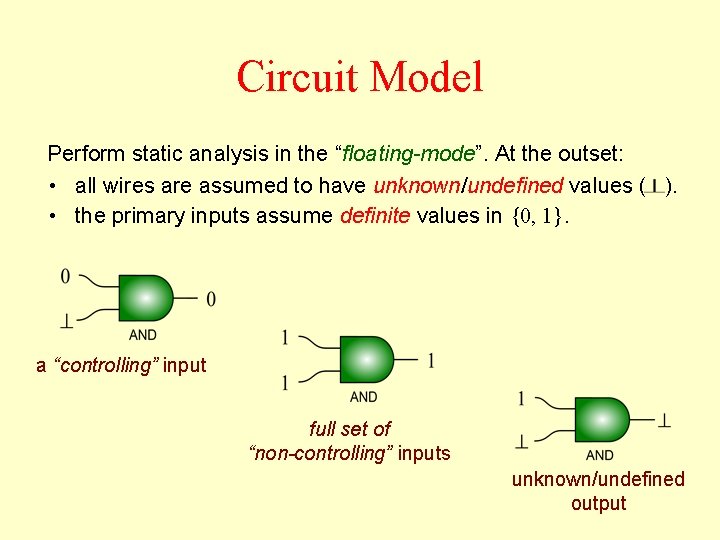
Circuit Model Perform static analysis in the “floating-mode”. At the outset: • all wires are assumed to have unknown/undefined values ( ). • the primary inputs assume definite values in {0, 1}. a “controlling” input full set of “non-controlling” inputs unknown/undefined output

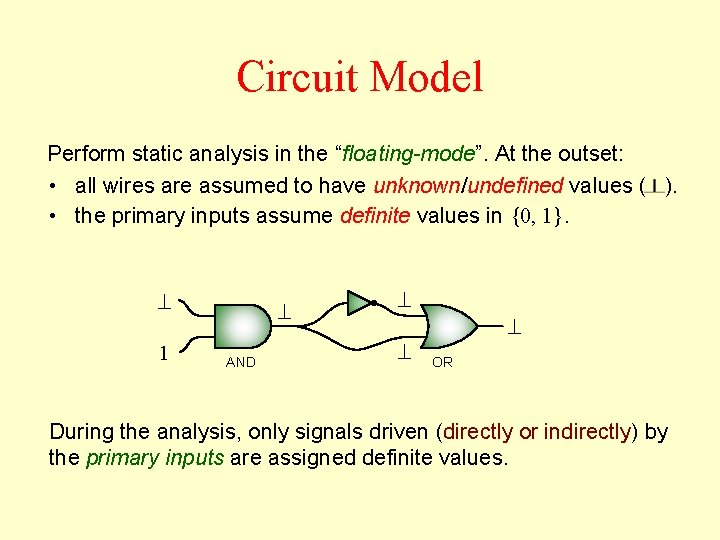
Circuit Model Perform static analysis in the “floating-mode”. At the outset: • all wires are assumed to have unknown/undefined values ( ). • the primary inputs assume definite values in {0, 1}. ^ 1 ^ AND ^ ^ ^ OR During the analysis, only signals driven (directly or indirectly) by the primary inputs are assigned definite values.

Circuit Model Up-bounded inertial delay model. Ensures monotone speed-up property. AND each gate has delay in [0, td]

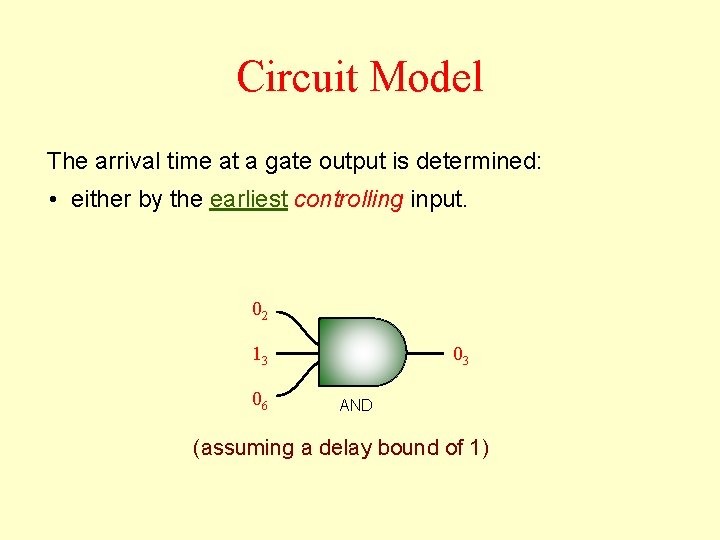
Circuit Model The arrival time at a gate output is determined: • either by the earliest controlling input. 02 13 06 03 AND (assuming a delay bound of 1)

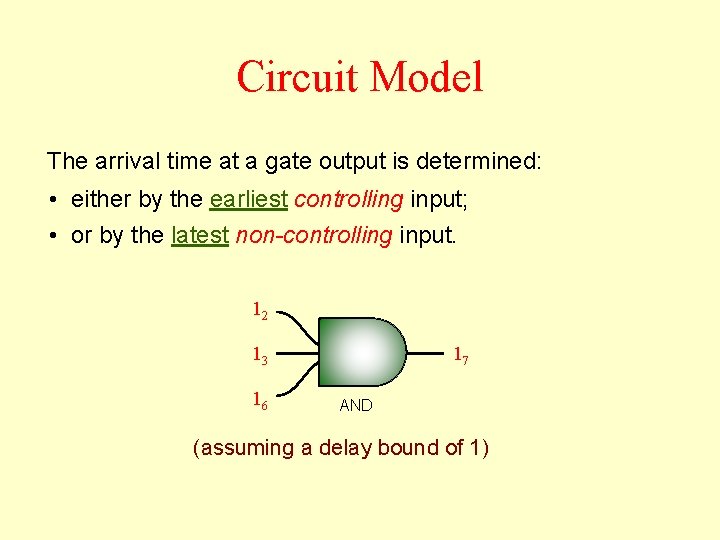
Circuit Model The arrival time at a gate output is determined: • either by the earliest controlling input; • or by the latest non-controlling input. 12 13 16 17 AND (assuming a delay bound of 1)

Timing Analysis Characterize arrival times symbolically (with BDDs): : set of input assignments that produce 0 : set of input assignments that produce 1 Implicitly: set of input assignments for which output is

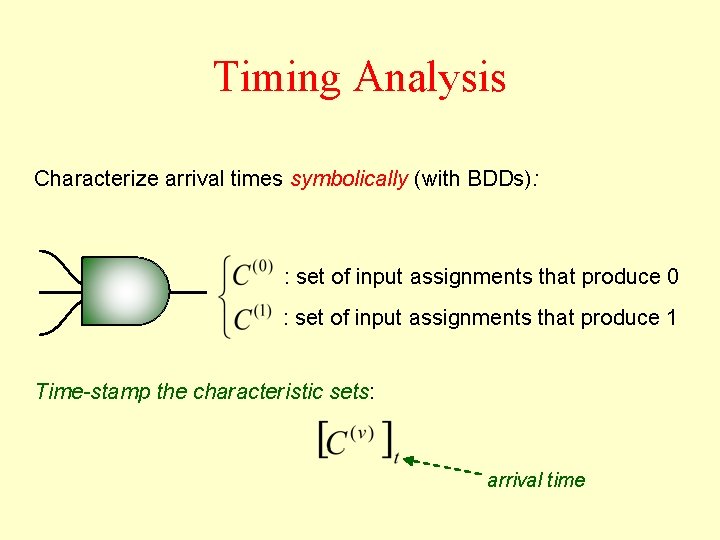
Timing Analysis Characterize arrival times symbolically (with BDDs): : set of input assignments that produce 0 : set of input assignments that produce 1 Time-stamp the characteristic sets: arrival time

Initialization internal signals: primary inputs: x

Propagation If there is a change in the characteristic set of a gate’s fan-in: For a controlling input value v, producing an output value w,

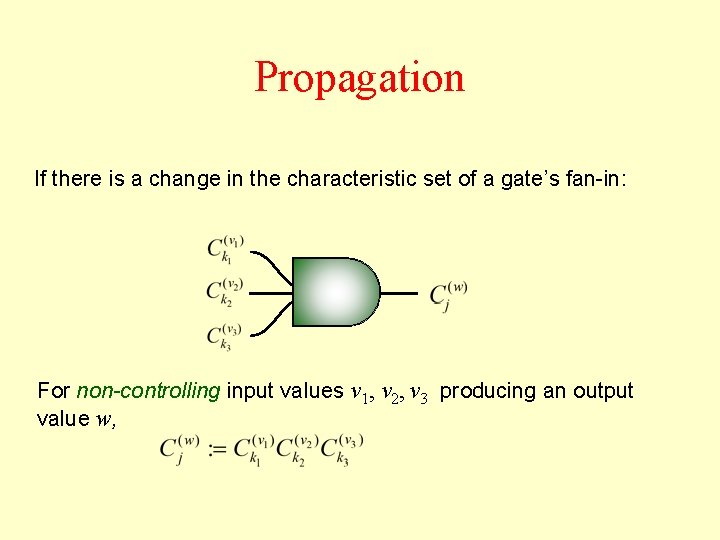
Propagation If there is a change in the characteristic set of a gate’s fan-in: For non-controlling input values v 1, v 2, v 3 producing an output value w,

Propagation If there is a change in the characteristic set of a gate’s fan-in: delay in [0, td] If changes as a result, update its time-stamp:

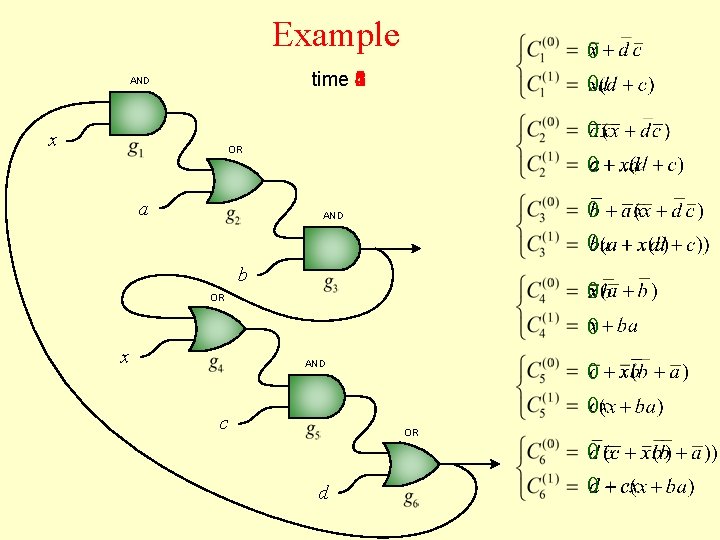
Example 0 0 time 6 1 2 3 4 5 AND x 0 0 OR a 0 0 AND b 0 0 OR x 0 0 AND c OR d 0 0

Timing Analysis • The algorithm terminates since the cardinality of each set increases over time; at most. • The circuit is combinational iff the “care” set of input assignments is contained within for each output gate gi. • The delay bounds on the arrival times for the output gates give a bound on the circuit delay.

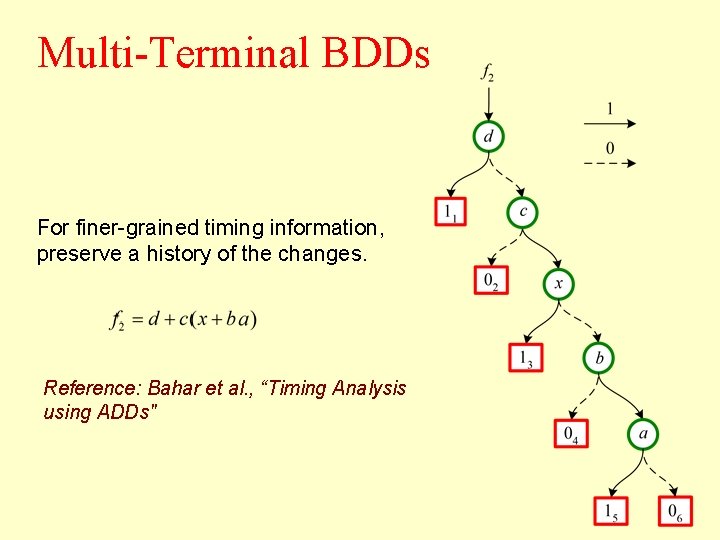
Multi-Terminal BDDs For finer-grained timing information, preserve a history of the changes. Reference: Bahar et al. , “Timing Analysis using ADDs"

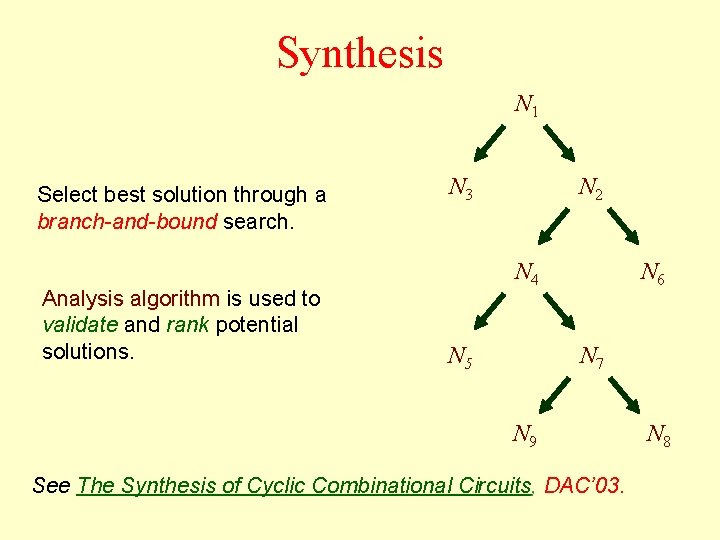
Synthesis N 1 Select best solution through a branch-and-bound search. Analysis algorithm is used to validate and rank potential solutions. N 3 N 2 N 4 N 5 N 6 N 7 N 9 See The Synthesis of Cyclic Combinational Circuits, DAC’ 03. N 8

Implementation: CYCLIFY Program • Incorporated synthesis methodology in a general logic synthesis environment (Berkeley SIS package). • Trials on wide range of circuits – randomly generated – benchmarks – industrial designs. • Conclusion: nearly all circuits of practical interest can be optimized with feedback.

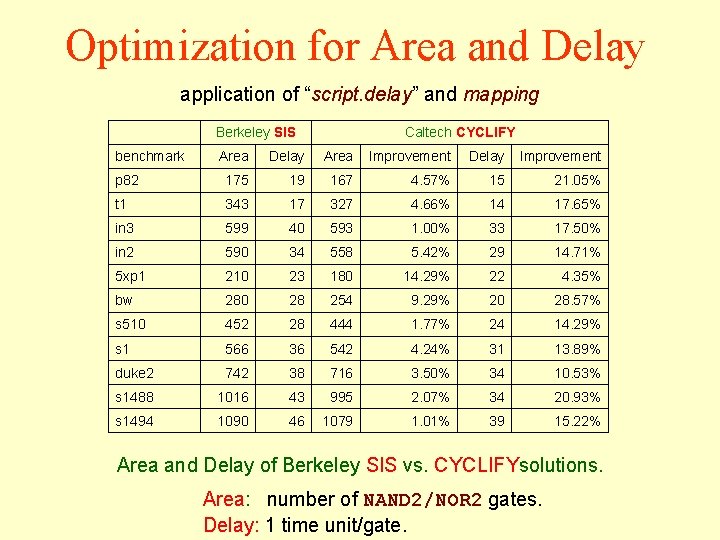
Optimization for Area and Delay application of “script. delay” and mapping Berkeley SIS benchmark Caltech CYCLIFY Area Delay Area Improvement Delay Improvement p 82 175 19 167 4. 57% 15 21. 05% t 1 343 17 327 4. 66% 14 17. 65% in 3 599 40 593 1. 00% 33 17. 50% in 2 590 34 558 5. 42% 29 14. 71% 5 xp 1 210 23 180 14. 29% 22 4. 35% bw 280 28 254 9. 29% 20 28. 57% s 510 452 28 444 1. 77% 24 14. 29% s 1 566 36 542 4. 24% 31 13. 89% duke 2 742 38 716 3. 50% 34 10. 53% s 1488 1016 43 995 2. 07% 34 20. 93% s 1494 1090 46 1079 1. 01% 39 15. 22% Area and Delay of Berkeley SIS vs. CYCLIFYsolutions. Area: number of NAND 2/NOR 2 gates. Delay: 1 time unit/gate.

Discussion Analysis through symbolic event propagation: • • Existing methods can be applied to cyclic circuits. Complexity is comparable for cyclic and acyclic circuits. Synthesis strategies targeting area and delay: • Nearly all circuits can be optimized with cycles. • Optimizations are significant.

Future Directions • Apply more realistic timing models for analysis. • Use more efficient symbolic techniques (e. g. , use boolean satisfiability (SAT)-based techniques). • Incorporate more sophisticated search heuristics into synthesis.