TimeSeries Data Management Yonsei University 2 nd Semester

Time-Series Data Management Yonsei University 2 nd Semester, 2014 Sanghyun Park * The slides were extracted from the material presented at ICDM’ 01 by Eamonn Keogh

Contents ± ± Introduction, motivation Utility of similarity measurements Indexing time series Summary, conclusions

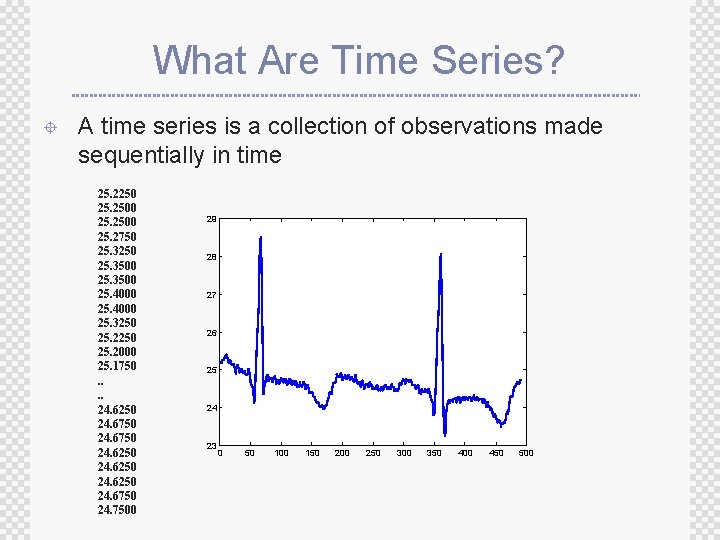
What Are Time Series? ± A time series is a collection of observations made sequentially in time 25. 2250 25. 2500 25. 2750 25. 3250 25. 3500 25. 4000 25. 3250 25. 2000 25. 1750. . 24. 6250 24. 6750 24. 7500 29 28 27 26 25 24 23 0 50 100 150 200 250 300 350 400 450 500

Time Series Are Ubiquitous (1/2) ± People measure things … ® The presidents approval rating ® Their blood pressure ® The annual rainfall in Riverside ® The value of their Yahoo stock ® The number of web hits per second ± And things change over time and thus time series occur in virtually every medical, scientific and business domain

Time Series Are Ubiquitous (2/2) ± A random sample of 4, 000 graphics from 15 of the world’s newspapers published from 1974 to 1989 found that more than 75% of all graphics were time series

Time Series Similarity ± Defining the similarity between two time series is at the heart of most time series data mining applications/tasks ± Thus time series similarity will be the primary focus of this lecture

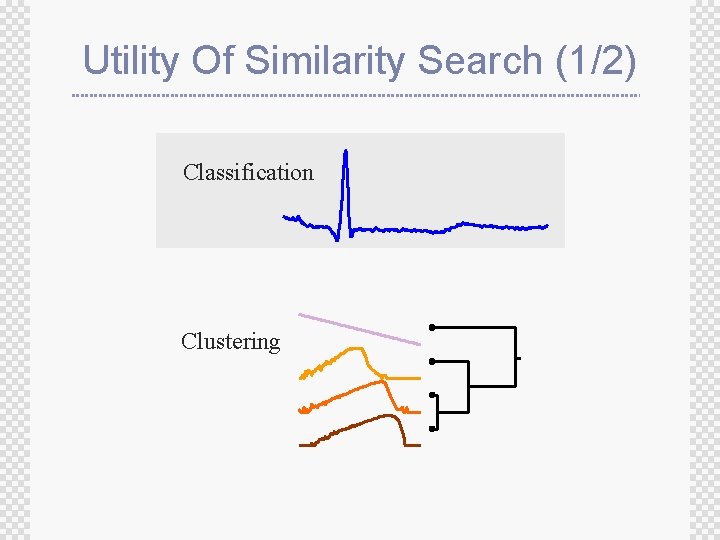
Utility Of Similarity Search (1/2) Classification Clustering

Utility Of Similarity Search (2/2) Rule Discovery s = 0. 5 10 c = 0. 3 Query by Content Query Q (template)

Challenges Of Research On Time Series (1/3) ± How do we work with very large databases? ® 1 hour of ECG data: 1 gigabyte ® Typical web log: 5 gigabytes per week ® Space shuttle database: 158 gigabytes and growing ® Macho database: 2 terabytes, updated with 3 gigabytes per day ± Since most of the data lives on disk (or tape), we need a representation of the data we can efficiently manipulate

Challenges Of Research On Time Series (2/3) ± We are dealing with subjective notions of similarity ± The definition of similarity depends on the user, the domain, and the task at hand. We need to handle this subjectivity

Challenges Of Research On Time Series (3/3) ± Miscellaneous data handling problems ® Differing data formats ® Differing sampling rates ® Noise, missing values, etc

Whole Matching vs. Subsequence Matching (1/2) ± Whole matching Given a query Q, a reference database C, and a distance measure, find the Ci that best matches Q Query Q (template) 1 6 2 7 3 8 4 9 5 10 Database C C 6 is the best match

Whole Matching vs. Subsequence Matching (2/2) ± Subsequence matching Given a query Q, a reference database C, and a distance measure, find the location that best matches Q Query Q (template) Database C The best matching subsection

Motivation Of Similarity Search ± You go to the doctor because of chest pains. Your ECG looks strange … ± Your doctor wants to search a database to find similar ECGs, in the hope that they will offer clues about your condition … ± Two questions ® How do we define similar? ® How do we search quickly?

Defining Distance Measures ± Definition: Let O 1 and O 2 be two objects from the universe of possible objects. Their distance is denoted as D(O 1, O 2) ± What properties should a distance measure have? ® D(A, B) = D(B, A) ® D(A, A) = 0 ® D(A, B) = 0 IIf A=B ® D(A, B) ≤ D(A, C) + D(B, C) Symmetry Constancy of self-similarity Positivity Triangluar inequality

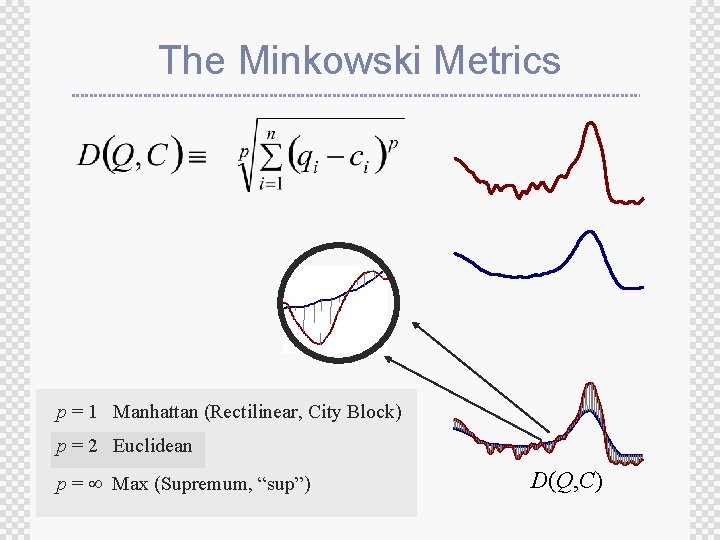
The Minkowski Metrics p = 1 Manhattan (Rectilinear, City Block) p = 2 Euclidean p = Max (Supremum, “sup”) D(Q, C)

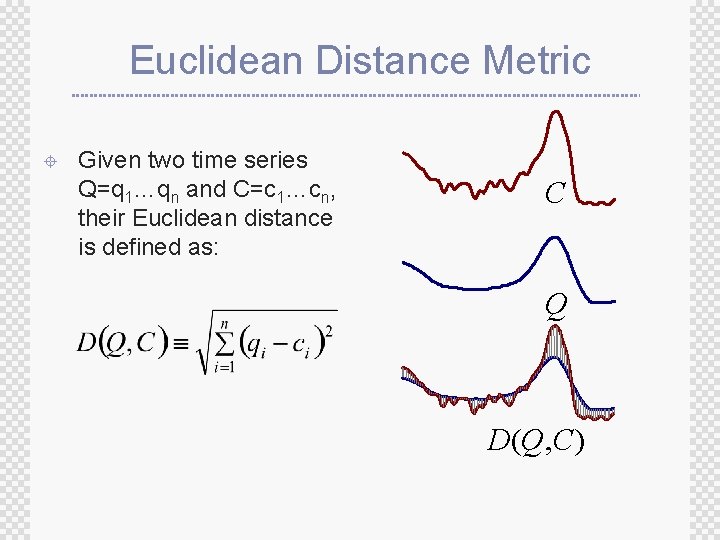
Euclidean Distance Metric ± Given two time series Q=q 1…qn and C=c 1…cn, their Euclidean distance is defined as: C Q D(Q, C)

Processing The Data Before Distance Calculation ± If we naively try to measure the distance between two “raw” time series, we may get very unintuitive results ± This is because Euclidean distance is very sensitive to some distortions in the data ± For most problems these distortions are not meaningful, and thus we can and should remove them ± Four most common distortions ® ® Offset translation Amplitude scaling Linear trend Noise

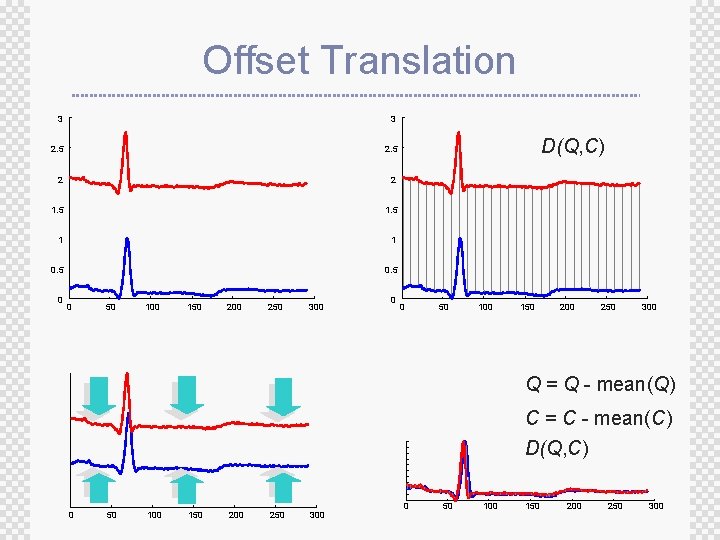
Offset Translation 3 3 2. 5 2 2 1. 5 1 1 0. 5 0 0 50 100 150 200 250 300 0 D(Q, C) 0 50 100 150 200 250 300 Q = Q - mean(Q) C = C - mean(C) D(Q, C) 0 50 100 150 200 250 300

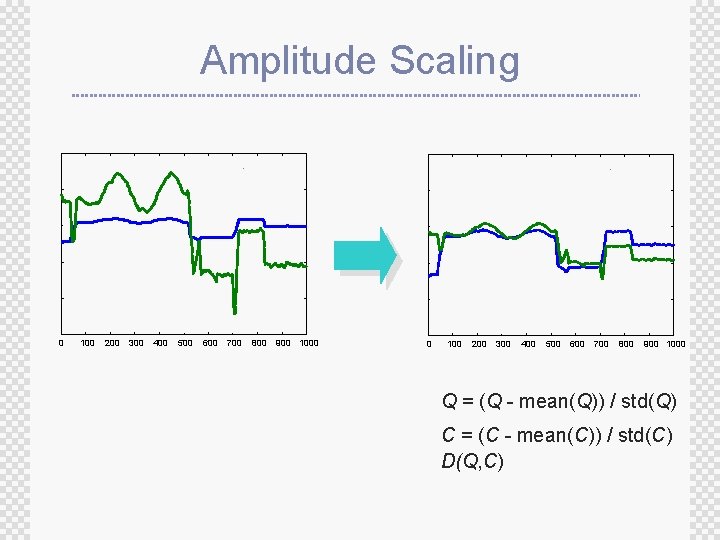
Amplitude Scaling 0 100 200 300 400 500 600 700 800 900 1000 Q = (Q - mean(Q)) / std(Q) C = (C - mean(C)) / std(C) D(Q, C)

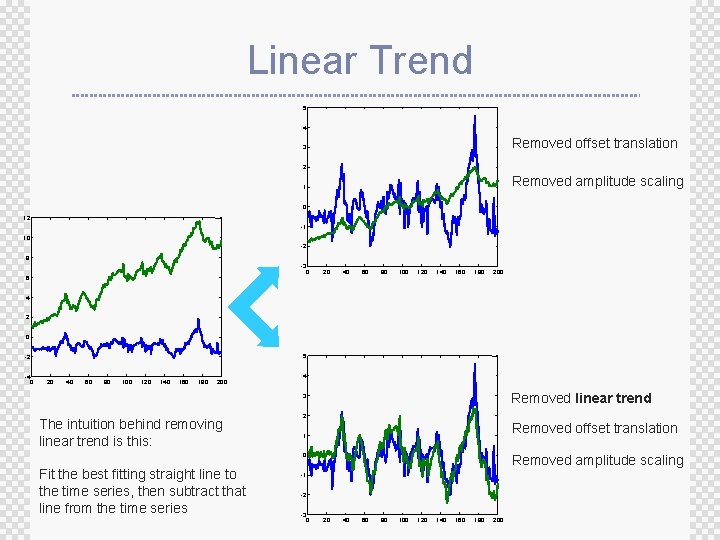
Linear Trend 5 4 Removed offset translation 3 2 Removed amplitude scaling 1 0 12 -1 10 -2 8 -3 0 6 20 40 60 80 100 120 140 160 180 200 4 2 0 5 -2 -4 0 20 40 60 80 100 120 140 160 180 200 4 Removed linear trend 3 The intuition behind removing linear trend is this: 2 Removed offset translation 1 0 Fit the best fitting straight line to the time series, then subtract that line from the time series Removed amplitude scaling -1 -2 -3 0 20 40 60 80 100 120 140 160 180 200

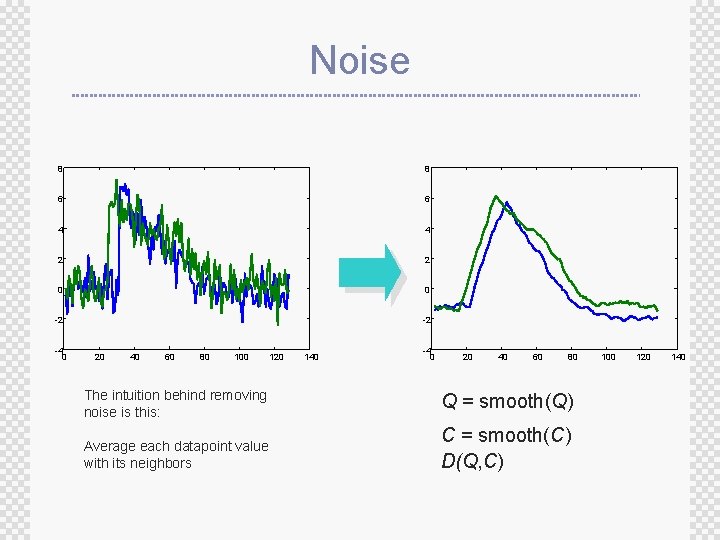
Noise 8 8 6 6 4 4 2 2 0 0 -2 -2 -4 0 20 40 60 80 100 120 140 -4 0 20 40 60 80 The intuition behind removing noise is this: Q = smooth(Q) Average each datapoint value with its neighbors C = smooth(C) D(Q, C) 100 120 140

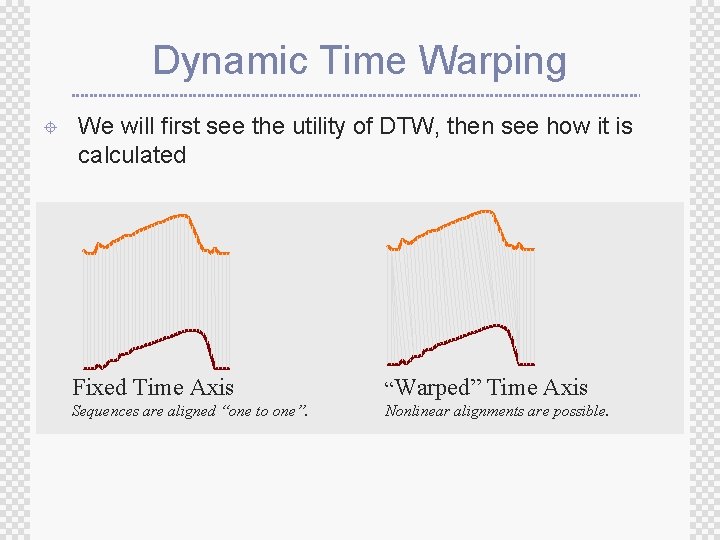
Dynamic Time Warping ± We will first see the utility of DTW, then see how it is calculated Fixed Time Axis “Warped” Time Axis Sequences are aligned “one to one”. Nonlinear alignments are possible.

Utility of DTW: Example I, Machine Learning Cylinder-Bell-Funnel Cylinder Funnel Bell ± This dataset has been studied in a machine learning context by many researchers ± Recall that, by definition, the instances of Cylinder-Bell. Funnel are warped in the time axis

Classification Experiment on C-B-F Dataset (1/2) ± Experimental settings ® Training data consists of 10 exemplars from each class ® (One) Nearest neighbor algorithm ® “Leaving-one-out” evaluation, averaged over 100 runs ± Results ® Error rate using Euclidean Distance: 26. 10% ® Error rate using Dynamic Time Warping: 2. 87% ® Time to classify one instance using Euclidean Distance: 1 sec ® Time to classify one instance using Dynamic Time Warping: 4, 320 sec

Classification Experiment on C-B-F Dataset (2/2) ± Dynamic time warping can reduce the error rate by an order of magnitude ± Its classification accuracy is competitive with sophisticated approaches like decision tree, boosting, neural networks, and Bayesian techniques ± But, it is slow …

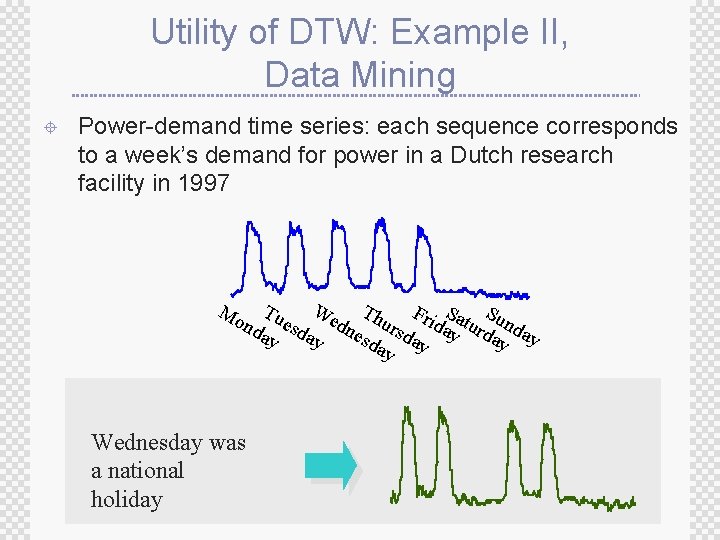
Utility of DTW: Example II, Data Mining ± Power-demand time series: each sequence corresponds to a week’s demand for power in a Dutch research facility in 1997 We Th Tu F S S e dn urs ridayaturd unda nd sd esd da ay ay ay y Mo Wednesday was a national holiday

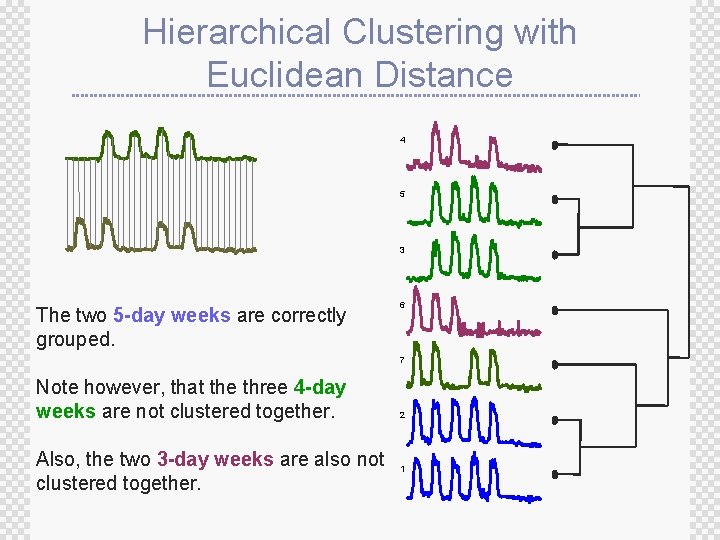
Hierarchical Clustering with Euclidean Distance 4 5 3 The two 5 -day weeks are correctly grouped. 6 7 Note however, that the three 4 -day weeks are not clustered together. Also, the two 3 -day weeks are also not clustered together. 2 1

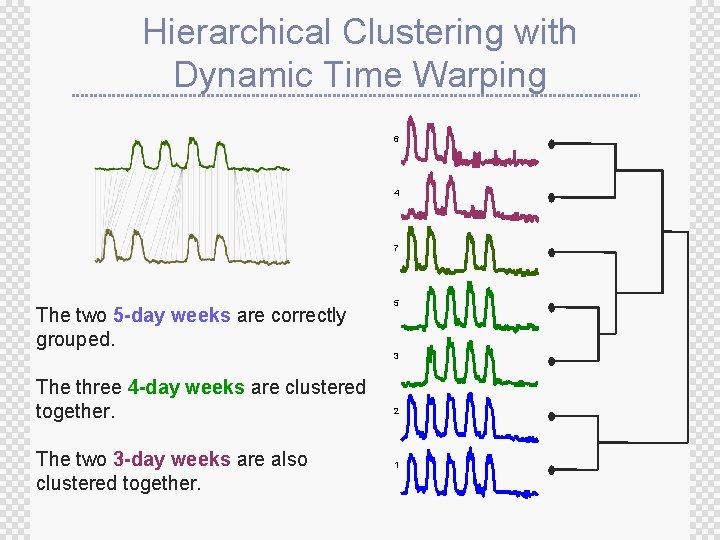
Hierarchical Clustering with Dynamic Time Warping 6 4 7 The two 5 -day weeks are correctly grouped. 5 3 The three 4 -day weeks are clustered together. The two 3 -day weeks are also clustered together. 2 1

Time Taken to Create Hierarchical Clustering of Power-Demand Time Series ± Time to create dendrogram using Euclidean Distance: 1. 2 seconds ± Time to create dendrogram using Dynamic Time Warping: 3. 40 hours

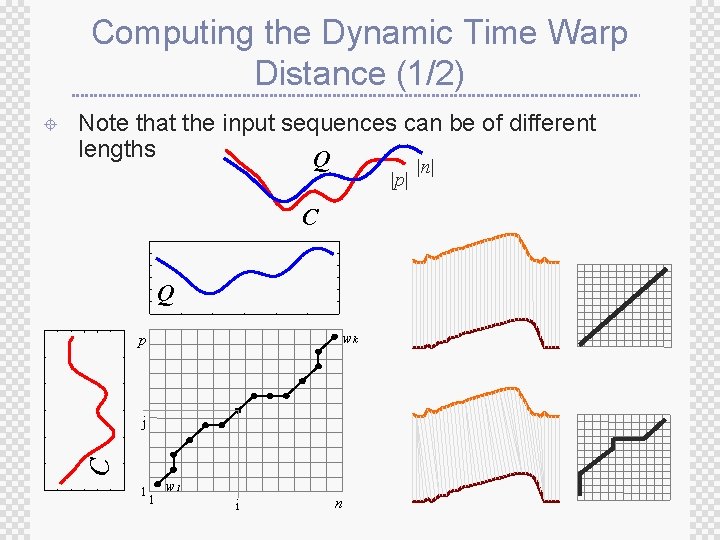
Computing the Dynamic Time Warp Distance (1/2) Note that the input sequences can be of different lengths Q |p| C Q wk p j C ± 1 1 w 1 i n |n|

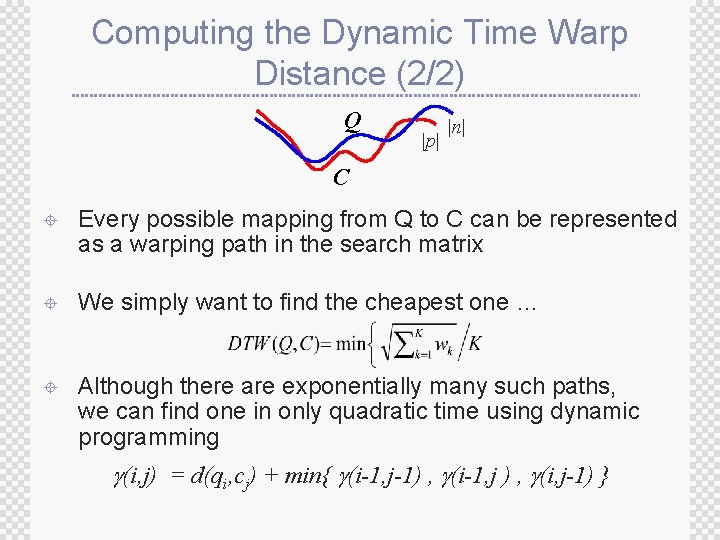
Computing the Dynamic Time Warp Distance (2/2) Q |p| |n| C ± Every possible mapping from Q to C can be represented as a warping path in the search matrix ± We simply want to find the cheapest one … ± Although there are exponentially many such paths, we can find one in only quadratic time using dynamic programming (i, j) = d(qi, cj) + min{ (i-1, j-1) , (i-1, j ) , (i, j-1) }

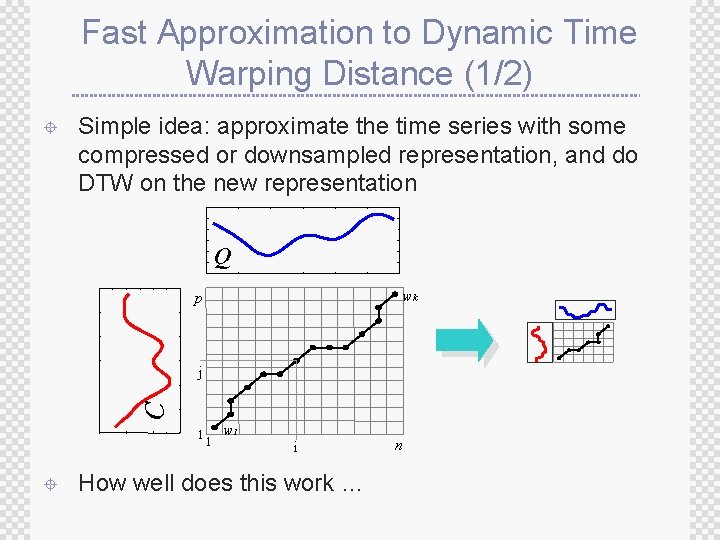
Fast Approximation to Dynamic Time Warping Distance (1/2) ± Simple idea: approximate the time series with some compressed or downsampled representation, and do DTW on the new representation Q wk p C j 1 ± 1 w 1 i How well does this work … n

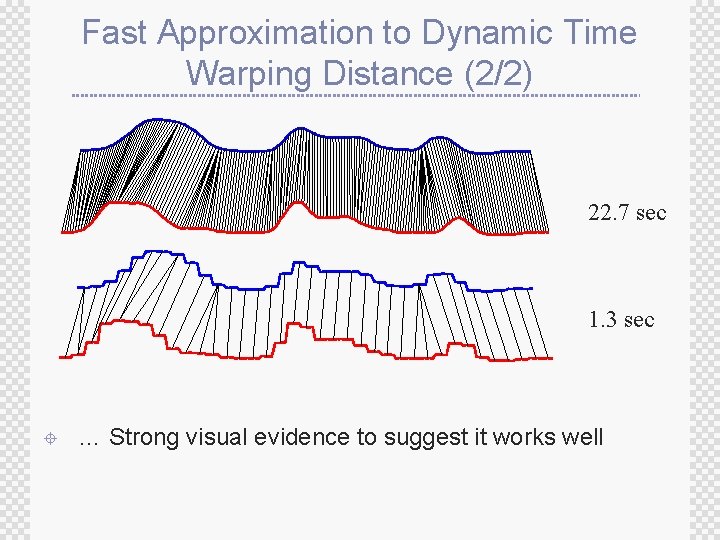
Fast Approximation to Dynamic Time Warping Distance (2/2) 22. 7 sec 1. 3 sec ± … Strong visual evidence to suggest it works well

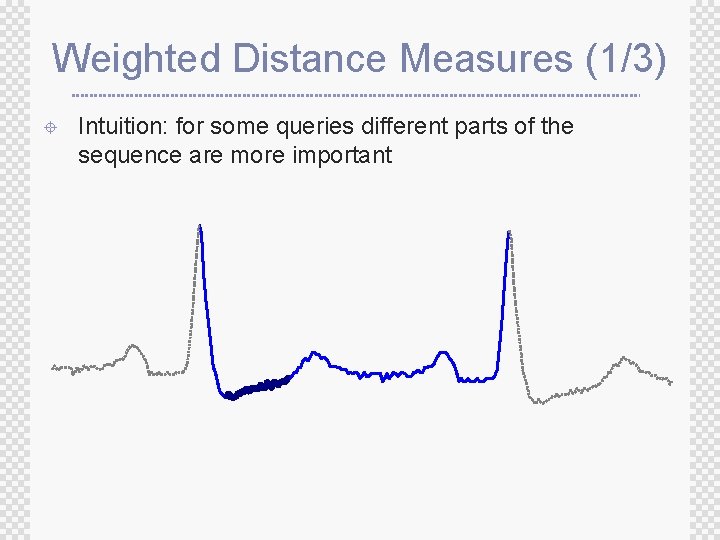
Weighted Distance Measures (1/3) ± Intuition: for some queries different parts of the sequence are more important

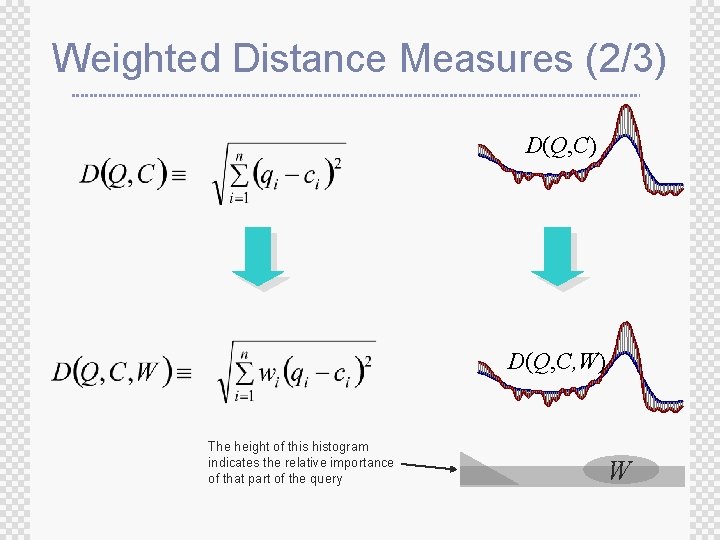
Weighted Distance Measures (2/3) D(Q, C, W) The height of this histogram indicates the relative importance of that part of the query W

Weighted Distance Measures (3/3) ± How do we set the weights? ± One possibility: relevance feedback which is the reformulation of a query in response to feedback provided by the user for the results of previous query Term Vector Term Weights [Jordan , Cow, Bull, River] [ 1 , 1 , 1 ] Search Display Results Gather Feedback Term Vector Term Weights [Jordan , Cow, Bull, River] [ 1. 1 , 1. 7 , 0. 3 , 0. 9 ] Update Weights

Indexing Time Series (1/6) ± We have seen techniques for assessing the similarity of two time series ± However we have not addressed the problem of finding the best match to a query in a large database … ± The obvious solution, to retrieve and examine every item (sequential scanning), simply does not scale to large datasets ± We need some way to index the data

Indexing Time Series (2/6) ± We can project time series of length n into n-dimension space ± The first value in C is the X-axis, the second value in C is the Y-axis, etc. ± One advantage of doing this is that we have abstracted away the details of “time series”, now all query processing can be imagined as finding points in space …

Indexing Time Series (3/6) ± We can project the query time series Q into the same ndimension space and simply look for the nearest points Q ± The problem is that we have to look at every point to find the nearest neighbor

Indexing Time Series (4/6) ± The Minkowski metrics have simple geometric interpolations Euclidean Weighted Euclidean Manhattan Max

Indexing Time Series (5/6) ± We can group clusters of datapoints with “boxes” called Minimum Bounding Rectangles (MBR) R 1 R 2 R 4 R 5 R 3 R 6 R 9 R 7 R 8 ± We can further recursively group MBRs into larger MBRs

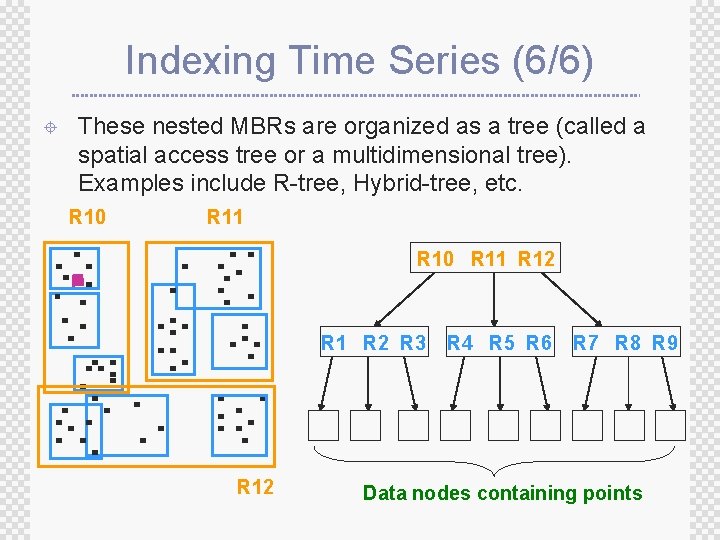
Indexing Time Series (6/6) ± These nested MBRs are organized as a tree (called a spatial access tree or a multidimensional tree). Examples include R-tree, Hybrid-tree, etc. R 10 R 11 R 12 R 1 R 2 R 3 R 12 R 4 R 5 R 6 R 7 R 8 R 9 Data nodes containing points

Dimensionality Curse (1/4) ± If we project a query into n-dimensional space, how many additional MBRs must we examine before we are guaranteed to find the best match? ± For the one dimensional space, the answer is clearly 2

Dimensionality Curse (2/4) ± If we project a query into n-dimensional space, how many additional MBRs must we examine before we are guaranteed to find the best match? ± For the two dimensional case, the answer is 8

Dimensionality Curse (3/4) ± If we project a query into n-dimensional space, how many additional MBRs must we examine before we are guaranteed to find the best match? ± For the three dimensional case, the answer is 26

Dimensionality Curse (4/4) ± If we project a query into n-dimensional space, how many additional MBRs must we examine before we are guaranteed to find the best match? ± More generally, in n-dimensional space we must examine 3 n-1 MBRs; n = 21 → 10, 460, 353, 201 MBRs ± This is known as the curse of dimensionality

Spatial Access Methods ± We can use Spatial Access Methods like the R-tree to index our data, but … ± The performance of R-trees degrades exponentially with the number of dimensions. Somewhere above 6 -20 dimensions the R-tree degrades to linear scanning ± Often we want to index time series with hundreds, perhaps even thousands of features

GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (1/8) ± Establish a distance metric from a domain expert ± Produce a dimensionality reduction technique that reduces the dimensionality of the data from n to N, where N can be efficiently handled by your favorite SAM ± Produce a distance measure defined on N dimensional representation of the data, and prove that it obeys Dindexspace(A, B) ≤ Dtrue(A, B) (lower bounding lemma) ± Plug into an off-the-shelve SAM

GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (2/8) ± We have 6 objects in 3 -D space. We issue a query to find all objects within 1 unit of the point (-3, 0, -2) A 3 2. 5 2 1. 5 C 1 B 0. 5 F 0 -0. 5 -1 3 2 D 1 0 -1 E -2 -3 -4 -3 -2 -1 0 1 2 3

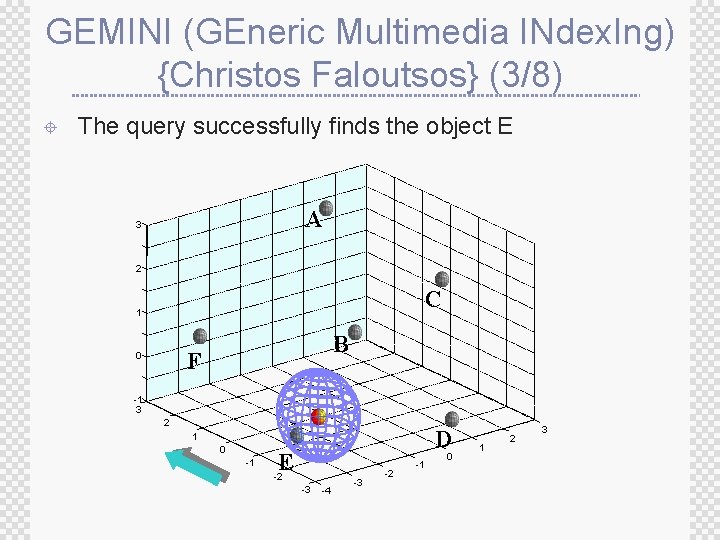
GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (3/8) ± The query successfully finds the object E A 3 2 C 1 B F 0 -1 3 2 D 1 0 -1 E -2 -3 -4 -3 -2 -1 0 1 2 3

GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (4/8) ± Consider what would happen if we issued the same query after reducing the dimensionality to 2, assuming the dimensionality technique obeys the lower bounding lemma ± Informally, it’s OK if objects appear “closer” in the dimensionality reduced space, than in the true space

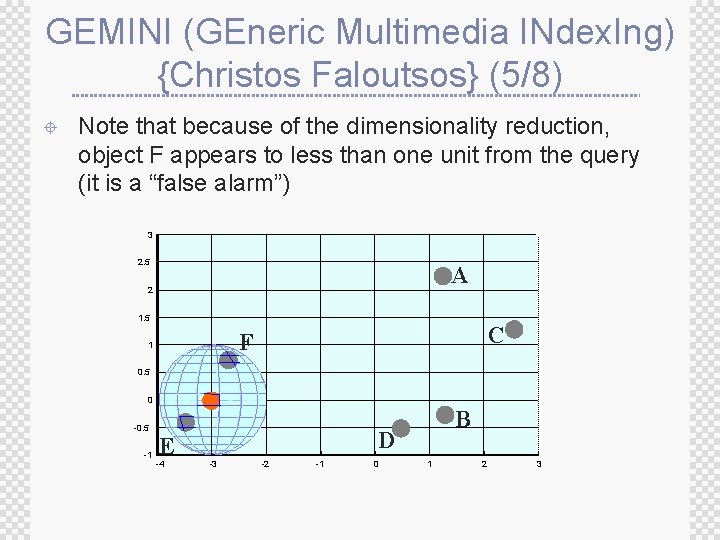
GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (5/8) ± Note that because of the dimensionality reduction, object F appears to less than one unit from the query (it is a “false alarm”) 3 2. 5 A 2 1. 5 C F 1 0. 5 0 -0. 5 -1 E -4 B D -3 -2 -1 0 1 2 3

GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (6/8) ± This is OK so long as it does not happen too much, since we can always retrieve it, then test it in the true, 3 -dimensional space ± This would leave us with just E, the correct answer

GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (7/8) ± Now, let’s consider a dimensionality reduction technique in which the lower bounding lemma is not satisfied ± Informally, some objects appear further apart in the dimensionality reduced space, than in the true space 3 2. 5 A 2 E 1. 5 1 C 0. 5 0 F -0. 5 -1 -4 -3 -2 -1 B D 0 1 2 3

GEMINI (GEneric Multimedia INdex. Ing) {Christos Faloutsos} (8/8) ± Note that because of the dimensionality reduction, object E appears to be more than one unit from the query (it is a “false dismissal”) ± This is unacceptable because we have failed to find the true answer set to our query ± These examples illustrate why the lower bounding lemma is so important ± Now all we have to do is to find a dimensionality reduction technique that obeys the lower bounding lemma, and we can index our time series

Notation for Dimensionality Reduction ± For the future discussion of dimensionality reduction we will assume that: ± M is the number of time series in our database ± n is the original dimensionality of the data ± N is the reduced dimensionality of the data ± Cratio = N/n is the compression ratio

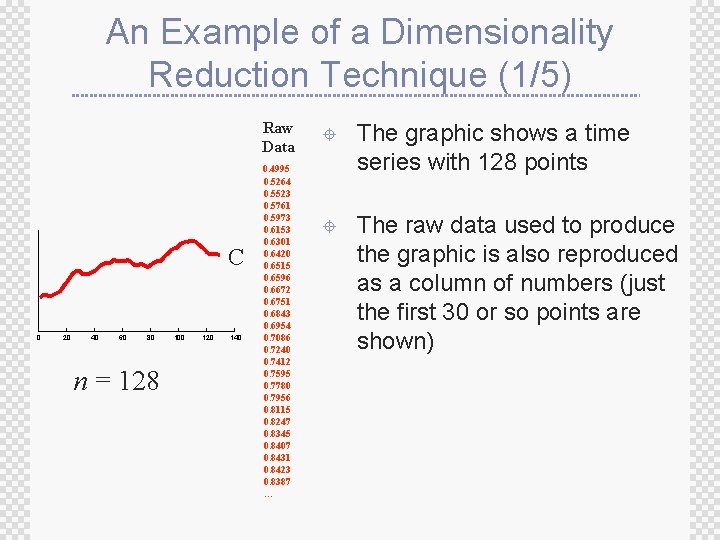
An Example of a Dimensionality Reduction Technique (1/5) Raw Data C 0 20 40 60 80 n = 128 100 120 140 0. 4995 0. 5264 0. 5523 0. 5761 0. 5973 0. 6153 0. 6301 0. 6420 0. 6515 0. 6596 0. 6672 0. 6751 0. 6843 0. 6954 0. 7086 0. 7240 0. 7412 0. 7595 0. 7780 0. 7956 0. 8115 0. 8247 0. 8345 0. 8407 0. 8431 0. 8423 0. 8387 … ± The graphic shows a time series with 128 points ± The raw data used to produce the graphic is also reproduced as a column of numbers (just the first 30 or so points are shown)

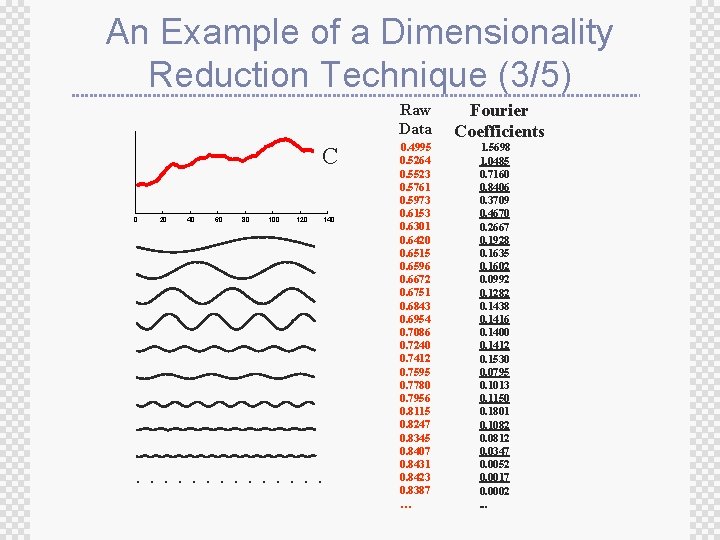
An Example of a Dimensionality Reduction Technique (2/5) ± We can decompose the data into 64 pure sine waves using the Discrete Fourier Transform (just the first few sine waves are shown in the next slide) ± The Fourier Coefficients are reproduced as a column of numbers (just the first 30 or so coefficients are shown) ± Note that at this stage we have not done dimensionality reduction; we have merely changed the representation

An Example of a Dimensionality Reduction Technique (3/5) Raw Data C 0 20 40 60 80 100 120 140 . . . 0. 4995 0. 5264 0. 5523 0. 5761 0. 5973 0. 6153 0. 6301 0. 6420 0. 6515 0. 6596 0. 6672 0. 6751 0. 6843 0. 6954 0. 7086 0. 7240 0. 7412 0. 7595 0. 7780 0. 7956 0. 8115 0. 8247 0. 8345 0. 8407 0. 8431 0. 8423 0. 8387 … Fourier Coefficients 1. 5698 1. 0485 0. 7160 0. 8406 0. 3709 0. 4670 0. 2667 0. 1928 0. 1635 0. 1602 0. 0992 0. 1282 0. 1438 0. 1416 0. 1400 0. 1412 0. 1530 0. 0795 0. 1013 0. 1150 0. 1801 0. 1082 0. 0812 0. 0347 0. 0052 0. 0017 0. 0002. . .

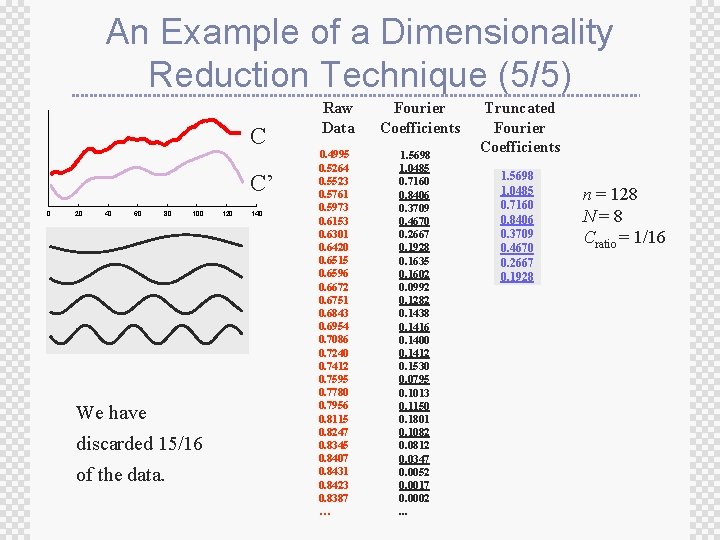
An Example of a Dimensionality Reduction Technique (4/5) ± Note that the first few sine waves tend to be the largest (equivalently, the magnitude of the Fourier coefficients tends to decrease as you move down the column) ± We can therefore truncate most of the small coefficients with little effect ± Instead of taking the first few coefficients, we could take the “best” coefficients ± This can help greatly in terms of approximation quality, but make indexing hard

An Example of a Dimensionality Reduction Technique (5/5) C C’ 0 20 40 60 80 100 We have discarded 15/16 of the data. 120 140 Raw Data 0. 4995 0. 5264 0. 5523 0. 5761 0. 5973 0. 6153 0. 6301 0. 6420 0. 6515 0. 6596 0. 6672 0. 6751 0. 6843 0. 6954 0. 7086 0. 7240 0. 7412 0. 7595 0. 7780 0. 7956 0. 8115 0. 8247 0. 8345 0. 8407 0. 8431 0. 8423 0. 8387 … Fourier Coefficients 1. 5698 1. 0485 0. 7160 0. 8406 0. 3709 0. 4670 0. 2667 0. 1928 0. 1635 0. 1602 0. 0992 0. 1282 0. 1438 0. 1416 0. 1400 0. 1412 0. 1530 0. 0795 0. 1013 0. 1150 0. 1801 0. 1082 0. 0812 0. 0347 0. 0052 0. 0017 0. 0002. . . Truncated Fourier Coefficients 1. 5698 1. 0485 0. 7160 0. 8406 0. 3709 0. 4670 0. 2667 0. 1928 n = 128 N=8 Cratio = 1/16

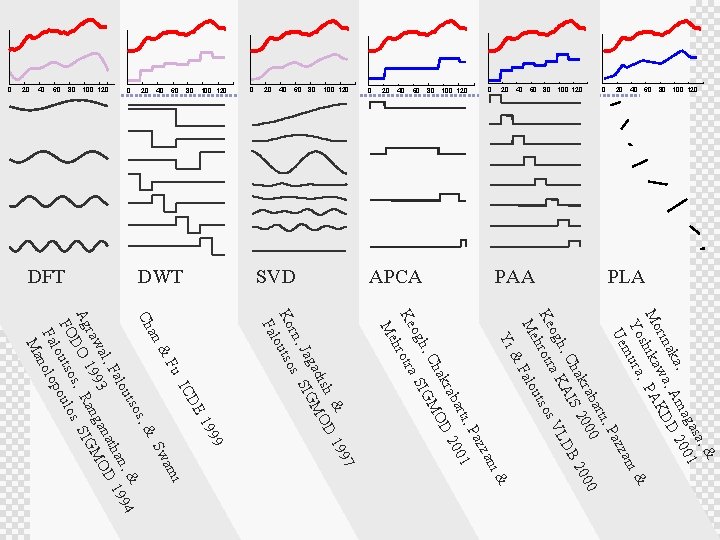
PLA PAA APCA SVD DWT DFT 20 40 60 80 100 120 40 20 0 80 100 120 60 40 20 0 a, & gas 1 , ma 200 aka , A D rin wa KD A Mo ika P h s , i& Yo mura zan Ue Paz rti, 0 aba 00 00 akr S 20 B 2 I Ch h, a KA LD og s. V Ke hrotr tso ou Me Fal & Yi i& zan Paz rti, 01 aba D 20 akr Ch GMO h, og tra SI hro Ke Me 7 99 & D 1 sh adi MO Jag. SIG s rn, Ko outso Fal 99 19 DE. . IC mi Fu & wa. S an Ch s, & tso & ou n, 1994 Fal tha al, 3 ana MOD raw 99 ang Ag DO 1 s, R s. SIG FO outso oulo p Fal nolo Ma

Directions for Future Research ± ± ± Time series in 2, 3, K dimensions Transforming other problems into time series problems Weighted distance measures Relevance feedback Approximation to SVD