TimeFrequency Characterization of Loudspeaker Responses Using Wavelet Analysis






























- Slides: 66

Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis D. Ponteggia 1 M. Di Cola 2 1 Audiomatica, Firenze, ITALY 2 Audio Labs Systems, Milano, ITALY 123 rd AES Convention, 2007 October 5 -8 New York, NY

Outline • Introduction • Loudspeaker Characterization • The Continuous Wavelet Transform • Practical Examples • Conclusions 2 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Motivation • This work is a direct spin-off of a previous work presented at AES 121 th in San Francisco last year: M. Di Cola, M. T. Hadelich, D. Ponteggia, D. Saronni, “Linear Phase Crossover Filters Advantages in Concert Sound Reinforcement Systems: a practical approach” • While trying to show the temporal effects of different crossover strategies, we found out that the available analysis tool were not easy to manage. • Phase-time relationship is well documented in literature but still not well understood by loudspeaker system designers. 3 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Motivation • We need simpler tools to visualize the loudspeaker system response. • This led us to research new tools to investigate the joint time-frequency characterization of loudspeaker systems. • After a brief literature research, we turned our attention to the Wavelet theory. • Even though Wavelet is a relatively recent topic, we found out that was yet used for loudspeaker impulse response analysis. 4 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Loudspeaker As Linear System • A loudspeaker (at least its linear model) can be fully described by means of its Impulse Response IR. • The IR is usually collected using computer based measuring instruments. Thanks to the fact that the IR is stored in a computer, post-processing is easily feasible. 5 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Fourier Transform Pair • By means of the Fourier transform pair (in its radial form) is it possible to switch back and forth from time domain to frequency domain: 6 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

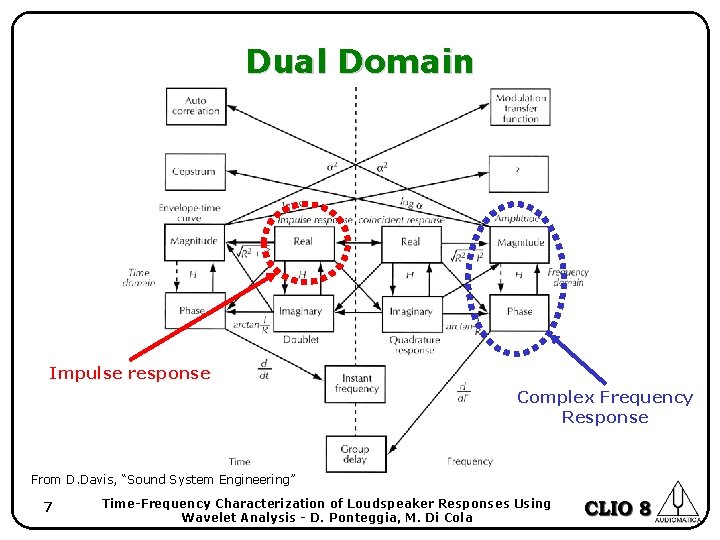
Dual Domain Impulse response Complex Frequency Response From D. Davis, “Sound System Engineering” 7 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

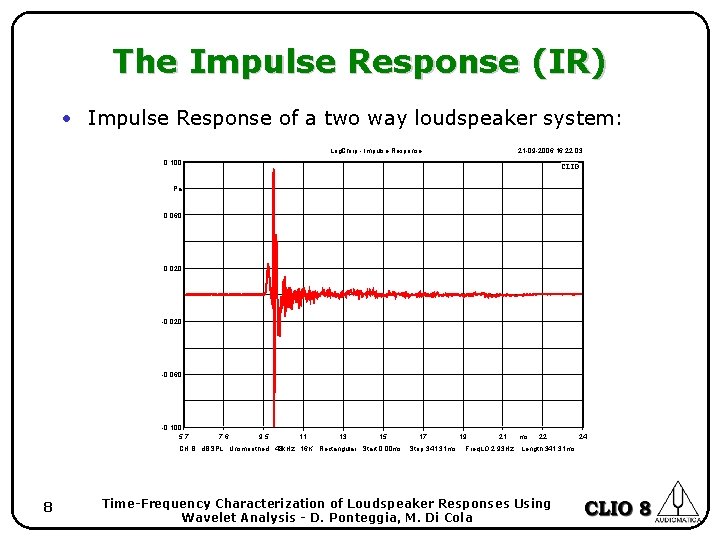
The Impulse Response (IR) • Impulse Response of a two way loudspeaker system: Log. Chirp - Impulse Response 21 -09 -2006 16. 22. 03 0. 100 CLIO Pa 0. 060 0. 020 -0. 060 -0. 100 5. 7 7. 6 9. 5 11 13 15 CH B d. BSPL Unsmoothed 48 k. Hz 16 K Rectangular Start 0. 00 ms 8 17 Stop 341. 31 ms 19 21 Freq. LO 2. 93 Hz ms 22 Length 341. 31 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola 24

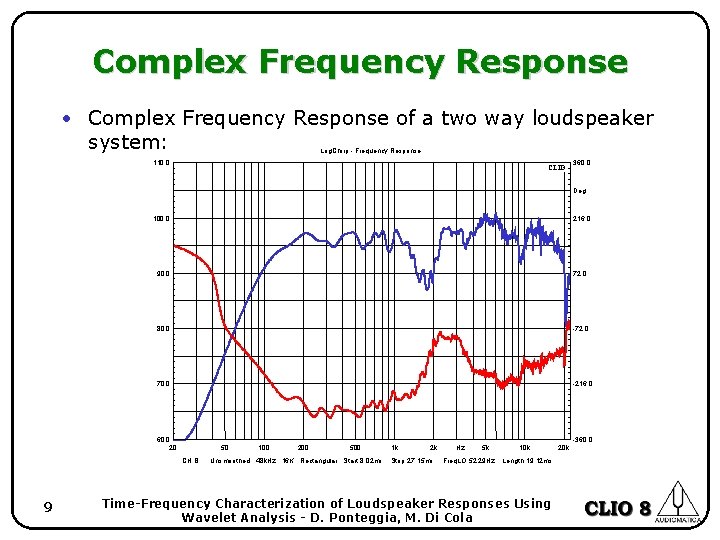
Complex Frequency Response • Complex Frequency Response of a two way loudspeaker system: Log. Chirp - Frequency Response 110. 0 CLIO 360. 0 Deg 100. 0 216. 0 90. 0 72. 0 80. 0 -72. 0 70. 0 -216. 0 60. 0 20 -360. 0 50 CH B 9 100 200 500 Unsmoothed 48 k. Hz 16 K Rectangular Start 8. 02 ms 1 k 2 k Stop 27. 15 ms Hz 5 k Freq. LO 52. 29 Hz 10 k Length 19. 12 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola 20 k

IR vs Complex Freq. Response • Impulse Response: – display very little information on the frequency domain – post-processing, as the ETC, can help to get more informations • Complex Frequency Response: – The phase part of the response is useful to understand the temporal behavior of the system (example crossover alignment) – unfortunately phase is buried into the propagation term – phase/time relationship is not simple as may appear 10 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Time Views • We have already showed that from the IR is not easy to infer the frequency components involved into the time distortion • Another time views has been developed to better understand the temporal behaviour of the system, but without gaining much more info on the spectral aspect. • Between them we have: – Step Response – ETC 11 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

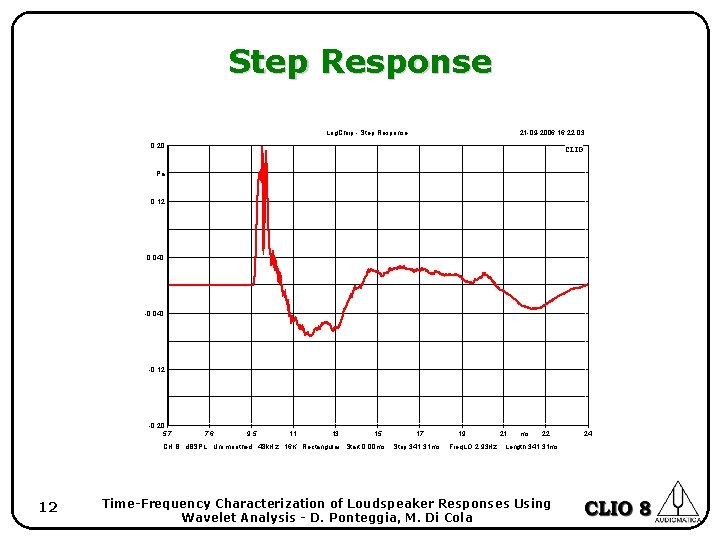
Step Response Log. Chirp - Step Response 21 -09 -2006 16. 22. 03 0. 20 CLIO Pa 0. 12 0. 040 -0. 12 -0. 20 5. 7 7. 6 9. 5 11 13 15 CH B d. BSPL Unsmoothed 48 k. Hz 16 K Rectangular Start 0. 00 ms 12 17 Stop 341. 31 ms 19 Freq. LO 2. 93 Hz 21 ms 22 Length 341. 31 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola 24

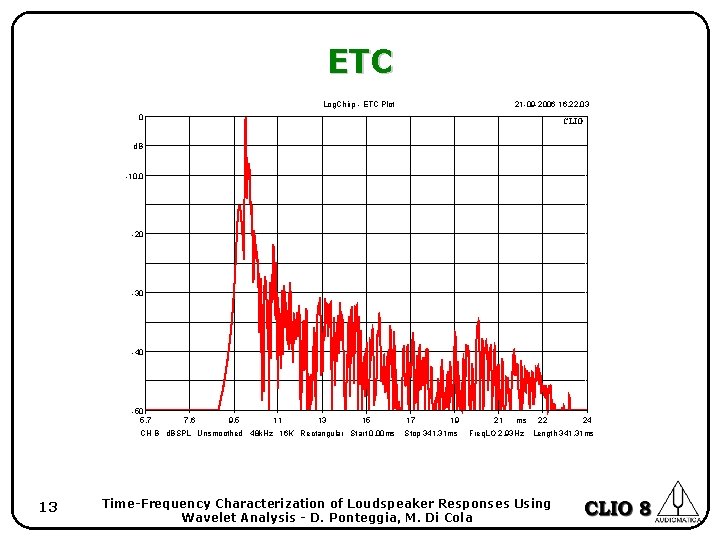
ETC Log. Chirp - ETC Plot 21 -09 -2006 16. 22. 03 0 CLIO d. B -10. 0 -20 -30 -40 -50 5. 7 7. 6 9. 5 11 13 15 CH B d. BSPL Unsmoothed 48 k. Hz 16 K Rectangular Start 0. 00 ms 13 17 19 Stop 341. 31 ms 21 ms Freq. LO 2. 93 Hz 22 24 Length 341. 31 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Spectral Views • The complex frequency response can be showed as magnitude and phase response. • It is common practice to check the time alignment of a loudspeaker system by looking at its phase response. • A direct relationship between phase and time delay is possible only for all-pass LTI systems: 14 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

A Closer Look To The Measurement Environment • A closer look to the measurement environment shows that the measured response is the sum of the loudspeaker system under test plus the sound propagation term: • The sound propagation can be modeled as a simple delay (in case of short distances). To recover the loudspeaker system phase response we need to remove the propagation delay: 15 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

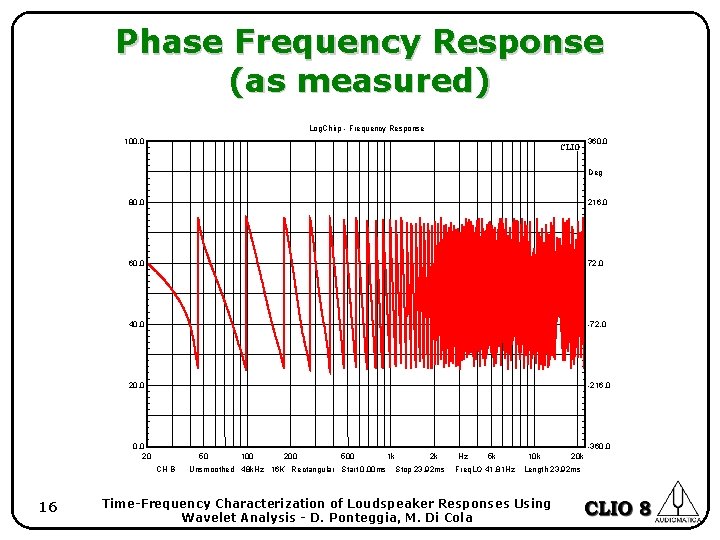
Phase Frequency Response (as measured) Log. Chirp - Frequency Response 100. 0 CLIO 360. 0 Deg 80. 0 216. 0 60. 0 72. 0 40. 0 -72. 0 20. 0 -216. 0 0. 0 20 -360. 0 50 CH B 16 100 200 500 Unsmoothed 48 k. Hz 16 K Rectangular Start 0. 00 ms 1 k 2 k Stop 23. 92 ms Hz 5 k Freq. LO 41. 81 Hz 10 k 20 k Length 23. 92 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Delay Removal Techniques • To remove the propagation delay we need to make some a priori assumption on the measurement model. • In the paper we have analyzed three commonly used techniques: – Impulse Time Maximum – Excess Phase Group Delay – Geometrical • We do not want to go into the details during this presentation, here we can state that choosing a “correct” value for the propagation delay is not straightforward! 17 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

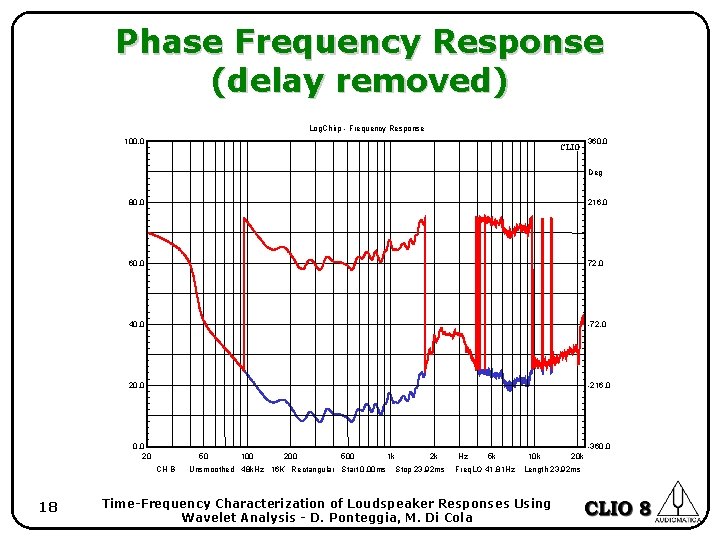
Phase Frequency Response (delay removed) Log. Chirp - Frequency Response 100. 0 CLIO 360. 0 Deg 80. 0 216. 0 60. 0 72. 0 40. 0 -72. 0 20. 0 -216. 0 0. 0 20 -360. 0 50 CH B 18 100 200 500 Unsmoothed 48 k. Hz 16 K Rectangular Start 0. 00 ms 1 k 2 k Stop 23. 92 ms Hz 5 k Freq. LO 41. 81 Hz 10 k 20 k Length 23. 92 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

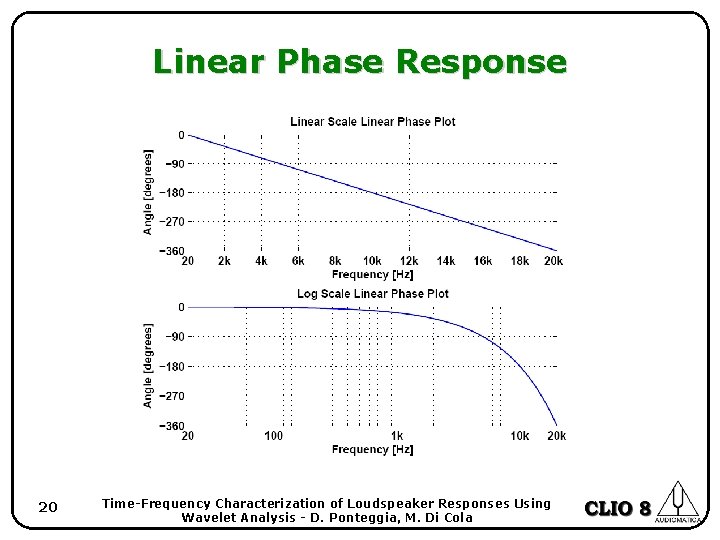
Linear Phase Response • An ideal perfect system will exhibit a flat magnitude response and a linear phase response (in a linear frequency axis graph) • It is engineering practice to look at frequency response graphs with frequency log scale • In case of complete removal of delay the phase plot must be flat, a deviation from linearity is easily seen and magnified by the log freq axis • In case of not complete removal of delay, the phase plot is a curve with negative slope, it could be more difficult to check deviations from linearity 19 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Linear Phase Response 20 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Joint Time-Frequency Views • Since we are not completely satisfied by the two previous views of the system response, there is a need to get some joint time-frequency descriptions: – Cumulative Spectral Decay CSD – Short Time Fourier Transform STFT – Wigner Distribution – Wavelet Analysis • While the CSD and STFT are well known and accepted, the Wigner and the Wavelet transform have not yet gained popularity. 21 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

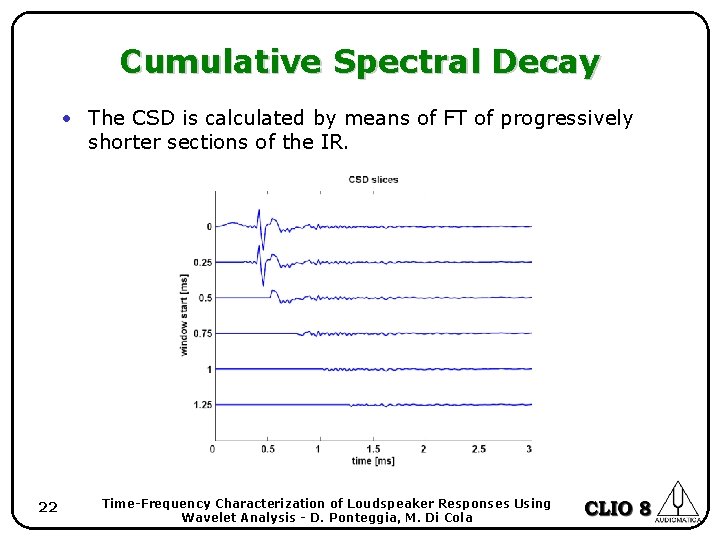
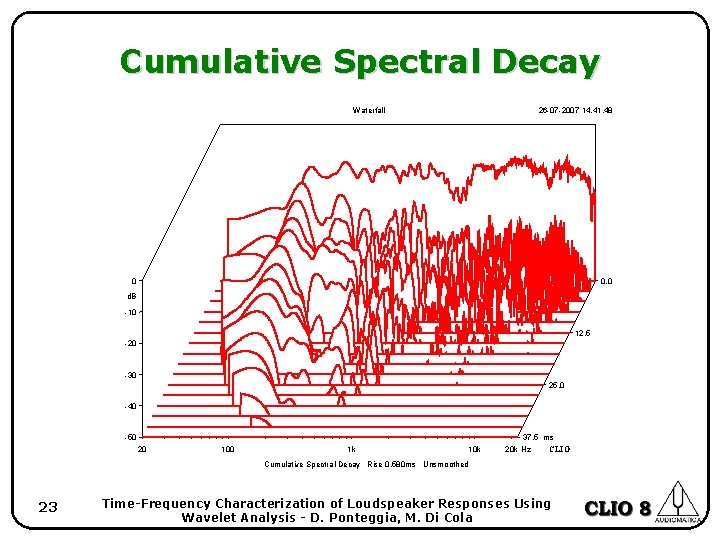
Cumulative Spectral Decay • The CSD is calculated by means of FT of progressively shorter sections of the IR. 22 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Cumulative Spectral Decay Waterfall 26 -07 -2007 14. 41. 48 0 0. 0 d. B -10 12. 5 -20 -30 25. 0 -40 -50 20 100 1 k 10 k 37. 5 ms 20 k Hz CLIO Cumulative Spectral Decay Rise 0. 580 ms Unsmoothed 23 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

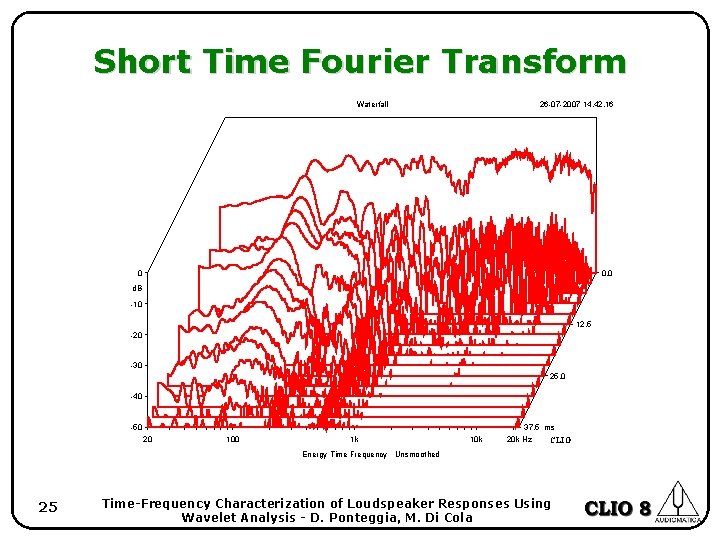
Short Time Fourier Transform • The idea of the STFT is to follow the temporal evolution of the IR and to apply FT to each section: • The main drawback of the STFT is its fixed resolution over the time-frequency plane. The choice of the FFT size is linked to the section length. • STFT is of little help to the analysis of wide-band longduration signals as the IR of a loudspeaker system. 24 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Short Time Fourier Transform Waterfall 26 -07 -2007 14. 42. 16 0 0. 0 d. B -10 12. 5 -20 -30 25. 0 -40 -50 20 100 1 k 10 k 37. 5 ms 20 k Hz CLIO Energy Time Frequency Unsmoothed 25 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

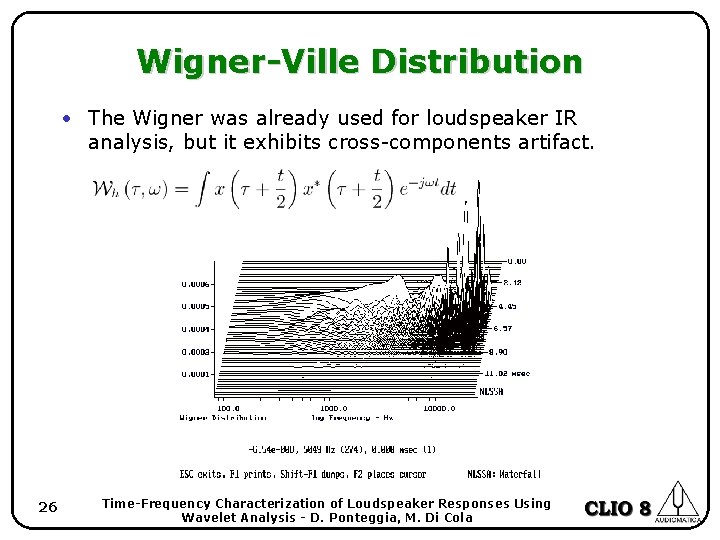
Wigner-Ville Distribution • The Wigner was already used for loudspeaker IR analysis, but it exhibits cross-components artifact. 26 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Continuous Wavelet Transform • The Continuous Wavelet Transform is defined as the inner product between the IR and a scaled and translated version of a function called “mother wavelet”: • The CWT can be wrote as: The factor 1/sqrt(a) is added to normalize the energy of the scaled wavelets. 27 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Continuous Wavelet Transform • The Wavelet Transform can be loosely interpreted as a correlation function between the IR and the scaled and translated wavelets. – low scale (high frequency) wavelets are short duration functions and they are good for the analysis of high frequency-short duration events – high scale (low frequency) wavelets are long duration functions and they are good for the analysis of low frequency-long duration events • The Wavelet Analysis can be understood as a constant. Q analysis – it is a good tool to investigate long duration wide-band signals 28 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Continuous Wavelet Transform • The uncertainty principle states that the temporal and bandwidth resolutions product: • It can be shown that the function with minimum product is the Gaussian pulse. • Therefore a good candidate as a mother wavelet is a modulated Gaussian pulse: 29 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

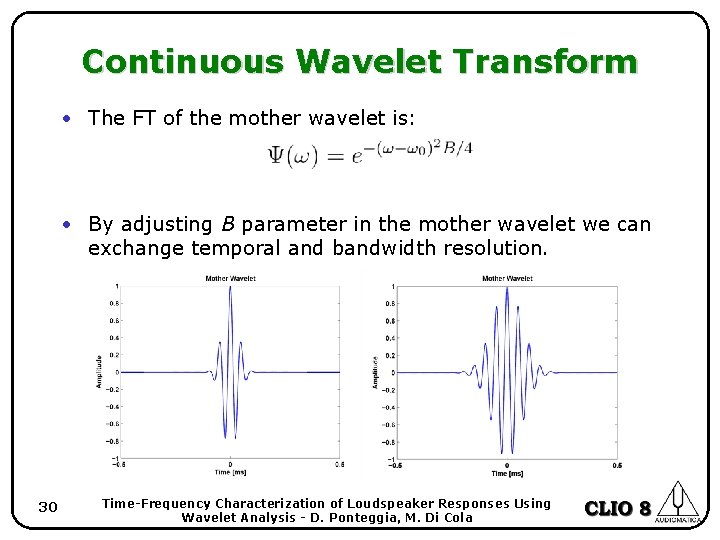
Continuous Wavelet Transform • The FT of the mother wavelet is: • By adjusting B parameter in the mother wavelet we can exchange temporal and bandwidth resolution. 30 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Continuous Wavelet Transform • The computation of the coefficients directly from the equation: is very expensive. • An alternative approach based on conventional FT can be used. For every scale a it is possible to calculate CWT coefficients: 31 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

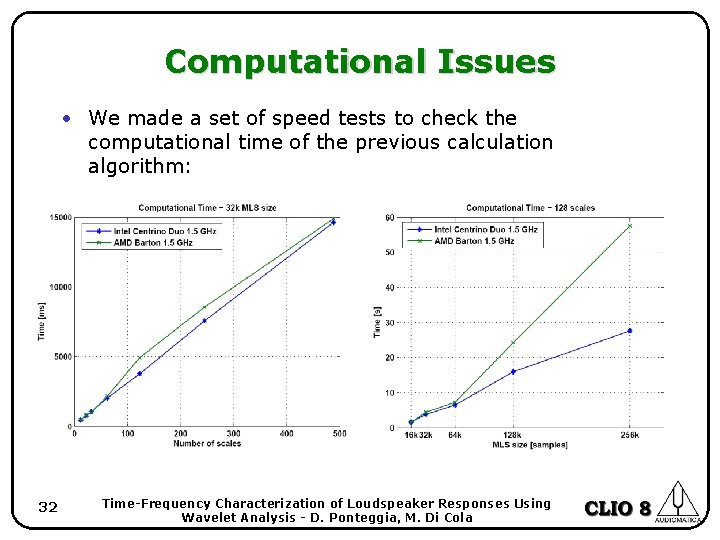
Computational Issues • We made a set of speed tests to check the computational time of the previous calculation algorithm: 32 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Scalogram Plot • Once the coefficient matrix is calculated we need to graphically represent the results. • The Spectrogram is a well known tool to show the energy of a signal in the time-frequency plane, it is defined as the squared modulus of the STFT. • The Scalogram is defined in a similar way as the squared modulus of the CWT. The energy of the signal is mapped in a time-scale plane: • It is possible to apply a transformation to get the usual timefrequency plane. 33 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

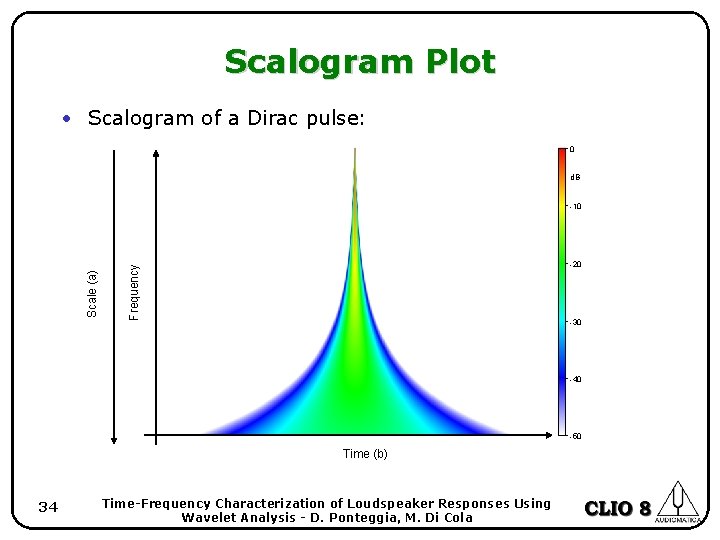
Scalogram Plot • Scalogram of a Dirac pulse: 0 d. B -20 Frequency Scale (a) -10 -30 -40 -50 Time (b) 34 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

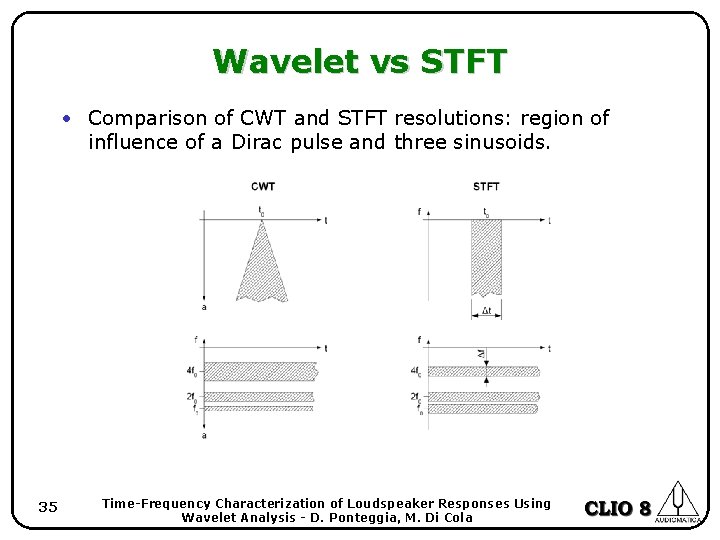
Wavelet vs STFT • Comparison of CWT and STFT resolutions: region of influence of a Dirac pulse and three sinusoids. 35 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Wavelet, STFT and Wigner • There is a strong link between Wigner-Ville distribution, spectrograms and scalograms. The latter two can be seen as “smoothed” versions of the first. 36 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

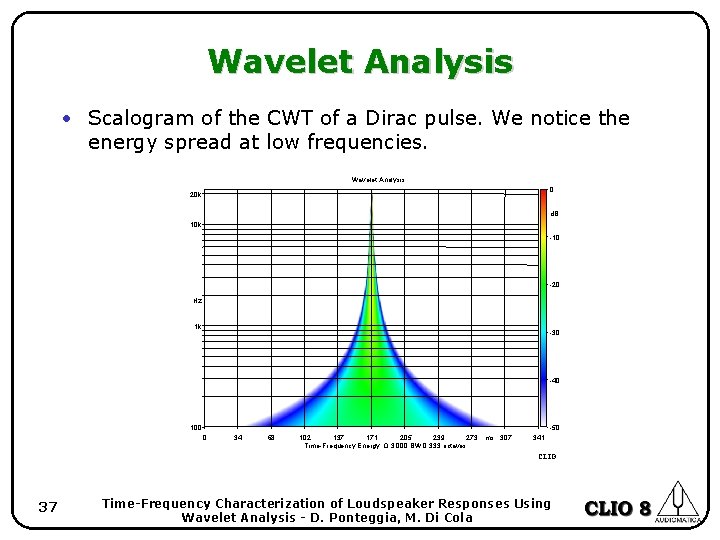
Wavelet Analysis • Scalogram of the CWT of a Dirac pulse. We notice the energy spread at low frequencies. Wavelet Analysis 0 20 k d. B 10 k -10 -20 Hz 1 k -30 -40 100 -50 0 34 68 102 137 171 205 239 273 ms 307 Time-Frequency Energy Q 3. 000 BW 0. 333 octaves 341 CLIO 37 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

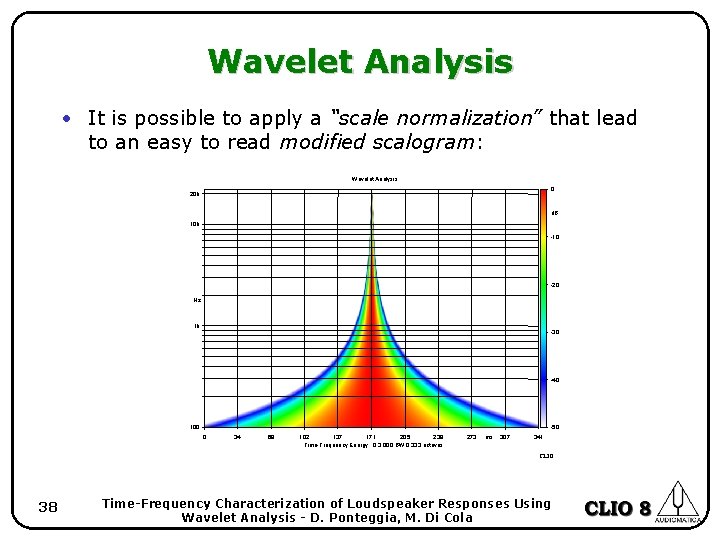
Wavelet Analysis • It is possible to apply a “scale normalization” that lead to an easy to read modified scalogram: Wavelet Analysis 0 20 k d. B 10 k -10 -20 Hz 1 k -30 -40 100 -50 0 34 68 102 137 171 205 239 Time-Frequency Energy Q 3. 000 BW 0. 333 octaves 273 ms 307 341 CLIO 38 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Wavelet Analysis • Wavelet Analysis of two way loudspeaker system 39 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

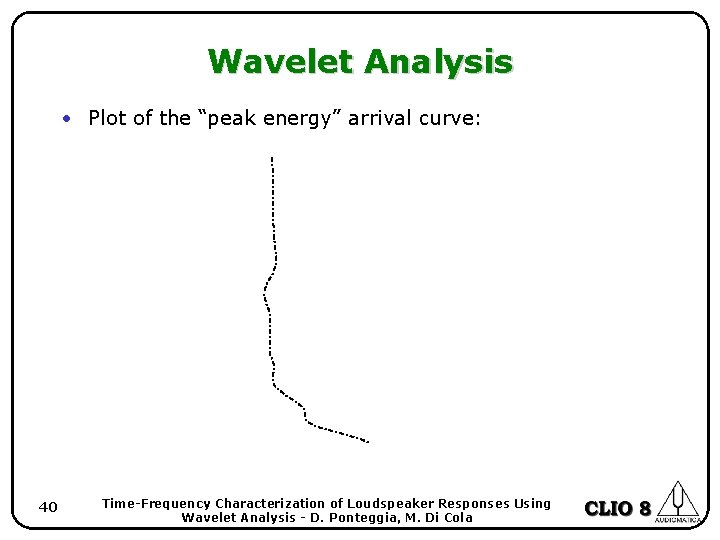
Wavelet Analysis • Plot of the “peak energy” arrival curve: 40 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

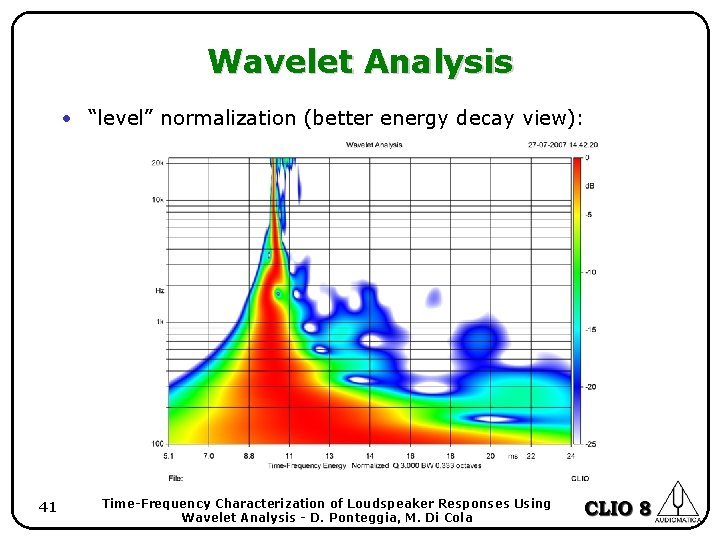
Wavelet Analysis • “level” normalization (better energy decay view): 41 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

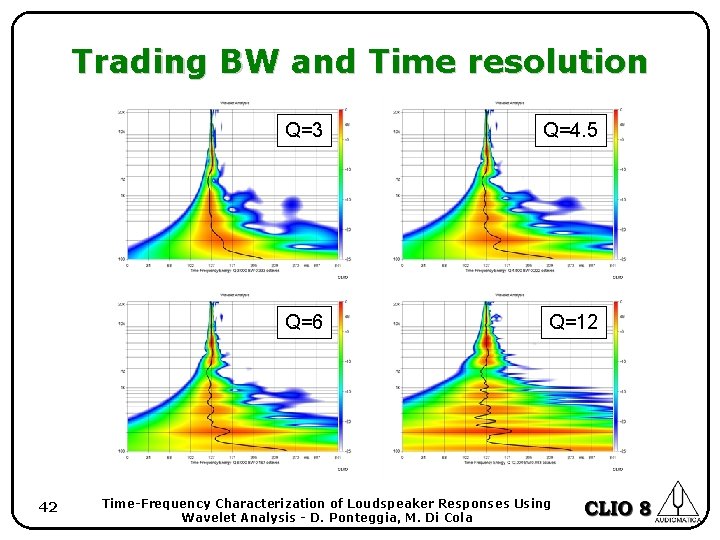
Trading BW and Time resolution 42 Q=3 Q=4. 5 Q=6 Q=12 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Real World Examples • We will show some examples of wavelet analysis on real world loudspeaker systems – – – 43 2 way professional 8” loudspeaker box 3 way vertical array element compression driver on CD horn Hi-Fi electrostatic loudspeaker Hi-Fi loudspeaker box with passive radiator Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

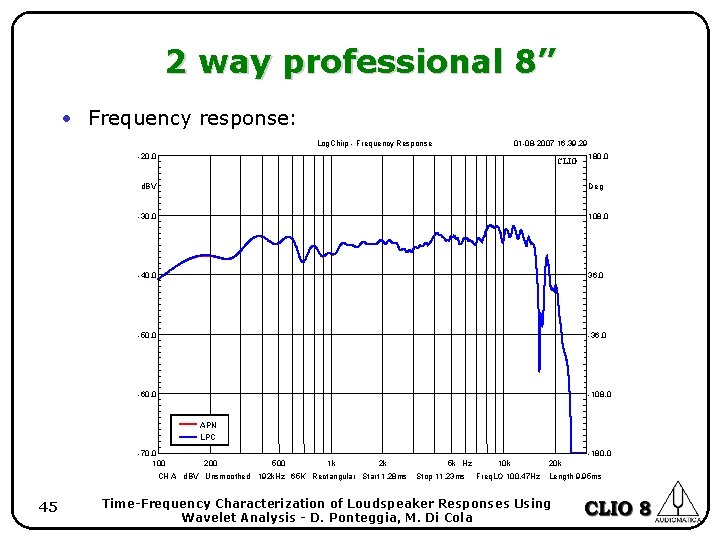
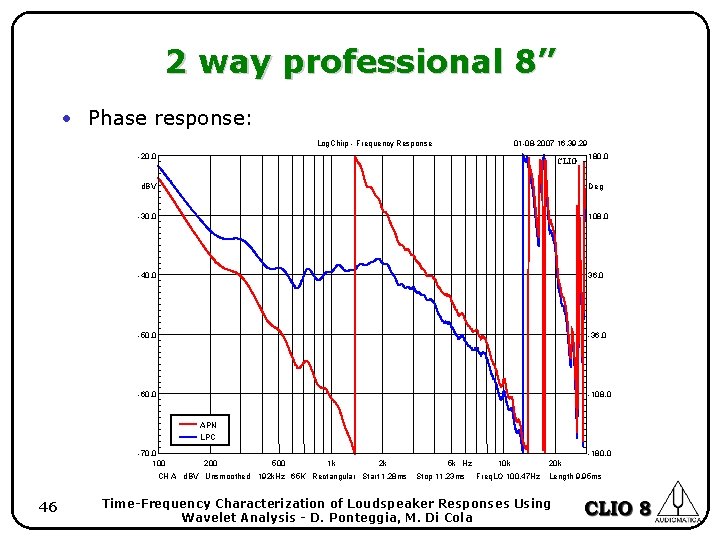
2 way professional 8” • This is a simple two way system equipped with a 8’’ cone woofer and 1’’ compression driver. • We analyze how two different crossover strategies affect the time alignment between drivers and which of the two perform better in term of time coherence. 44 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

2 way professional 8” • Frequency response: Log. Chirp - Frequency Response 01 -08 -2007 16. 39. 29 -20. 0 CLIO d. BV 180. 0 Deg -30. 0 108. 0 -40. 0 36. 0 -50. 0 -36. 0 -60. 0 -108. 0 APN LPC -70. 0 100 -180. 0 200 500 1 k 2 k CH A d. BV Unsmoothed 192 k. Hz 65 K Rectangular Start 1. 28 ms 45 5 k Hz Stop 11. 23 ms 10 k Freq. LO 100. 47 Hz 20 k Length 9. 95 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

2 way professional 8” • Phase response: Log. Chirp - Frequency Response 01 -08 -2007 16. 39. 29 -20. 0 CLIO d. BV 180. 0 Deg -30. 0 108. 0 -40. 0 36. 0 -50. 0 -36. 0 -60. 0 -108. 0 APN LPC -70. 0 100 -180. 0 200 500 1 k 2 k CH A d. BV Unsmoothed 192 k. Hz 65 K Rectangular Start 1. 28 ms 46 5 k Hz Stop 11. 23 ms 10 k Freq. LO 100. 47 Hz 20 k Length 9. 95 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

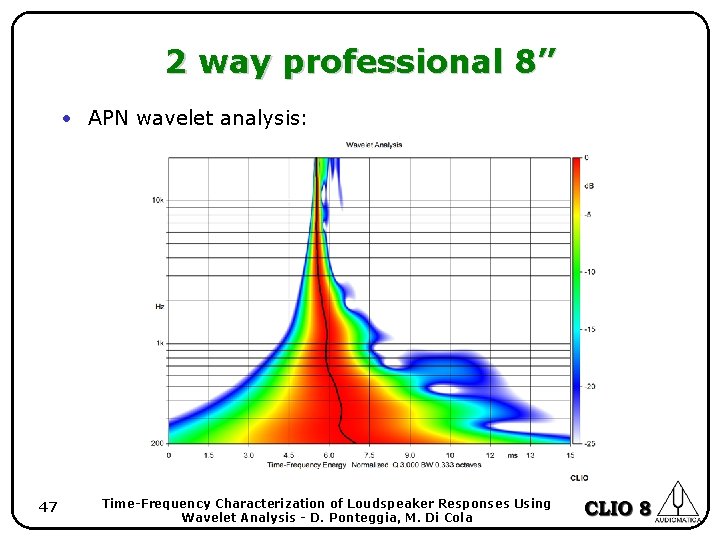
2 way professional 8” • APN wavelet analysis: 47 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

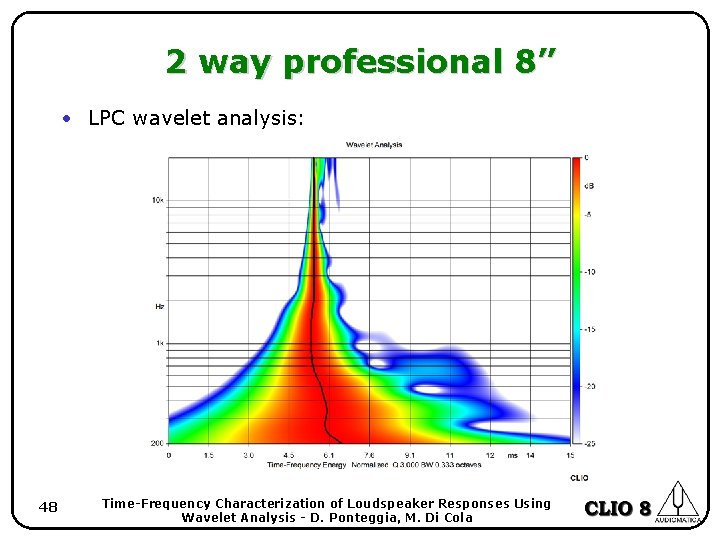
2 way professional 8” • LPC wavelet analysis: 48 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

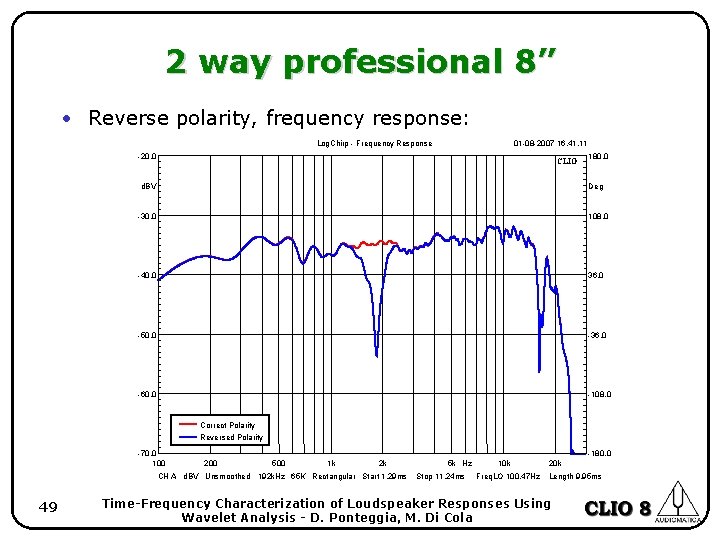
2 way professional 8” • Reverse polarity, frequency response: Log. Chirp - Frequency Response 01 -08 -2007 16. 41. 11 -20. 0 CLIO d. BV 180. 0 Deg -30. 0 108. 0 -40. 0 36. 0 -50. 0 -36. 0 -60. 0 -108. 0 Correct Polarity Reversed Polarity -70. 0 100 -180. 0 200 500 1 k 2 k CH A d. BV Unsmoothed 192 k. Hz 65 K Rectangular Start 1. 29 ms 49 5 k Hz Stop 11. 24 ms 10 k Freq. LO 100. 47 Hz 20 k Length 9. 95 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

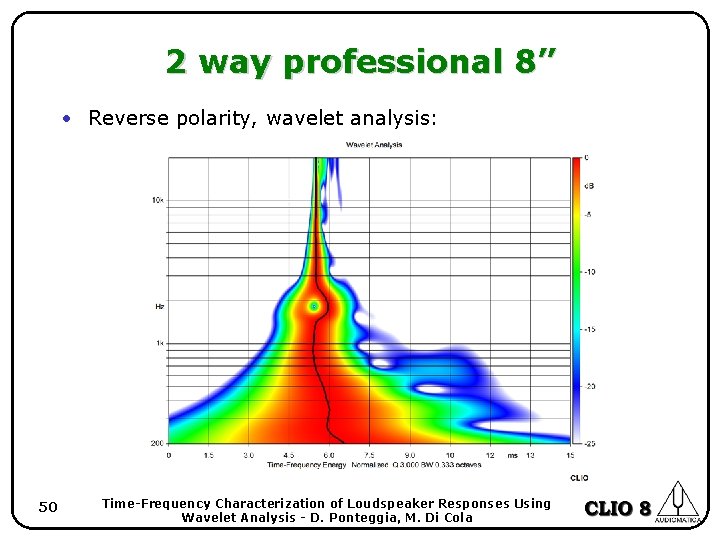
2 way professional 8” • Reverse polarity, wavelet analysis: 50 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

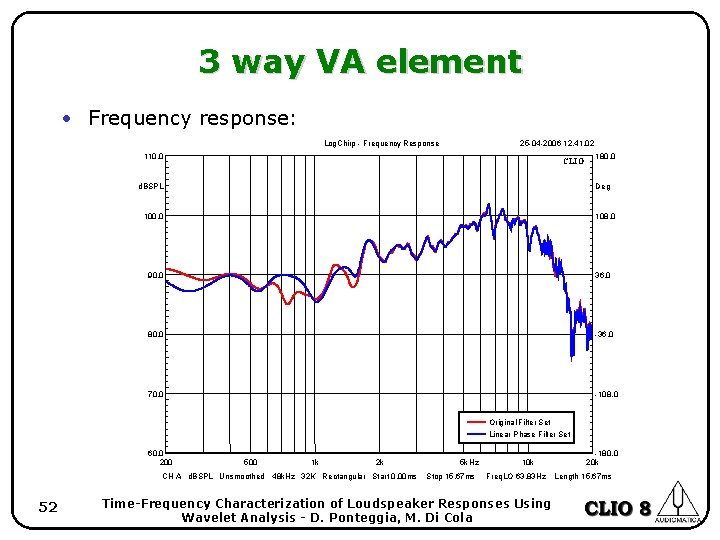
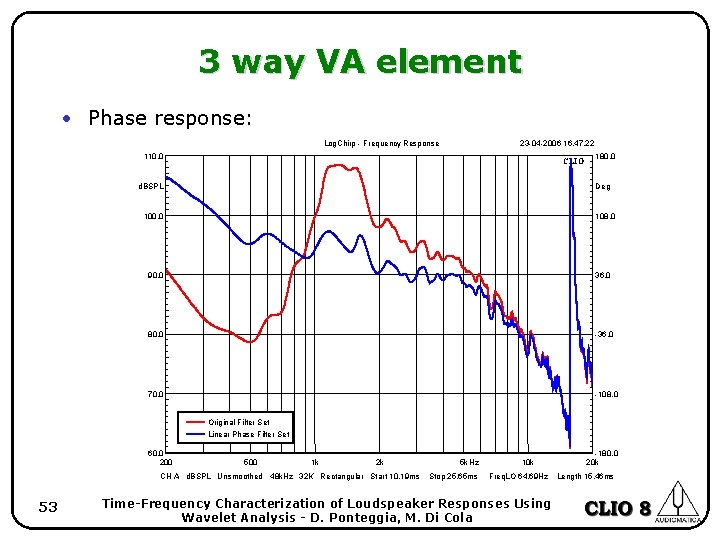
3 way VA element • Big format vertical array element. • Comparison between APN and LPC crossover strategies. • Frequency response almost identical (small differences), while phase response shows remarkably different responses. 51 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

3 way VA element • Frequency response: Log. Chirp - Frequency Response 25 -04 -2006 12. 41. 02 110. 0 CLIO d. BSPL 180. 0 Deg 100. 0 108. 0 90. 0 36. 0 80. 0 -36. 0 70. 0 -108. 0 Original Filter Set Linear Phase Filter Set 60. 0 200 500 1 k 2 k CH A d. BSPL Unsmoothed 48 k. Hz 32 K Rectangular Start 0. 00 ms 52 5 k Hz Stop 15. 67 ms 10 k Freq. LO 63. 83 Hz Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola -180. 0 20 k Length 15. 67 ms

3 way VA element • Phase response: Log. Chirp - Frequency Response 23 -04 -2006 16. 47. 22 110. 0 CLIO d. BSPL 180. 0 Deg 100. 0 108. 0 90. 0 36. 0 80. 0 -36. 0 70. 0 -108. 0 Original Filter Set Linear Phase Filter Set 60. 0 200 500 1 k 2 k CH A d. BSPL Unsmoothed 48 k. Hz 32 K Rectangular Start 10. 19 ms 53 5 k Hz Stop 25. 65 ms 10 k Freq. LO 64. 69 Hz Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola -180. 0 20 k Length 15. 46 ms

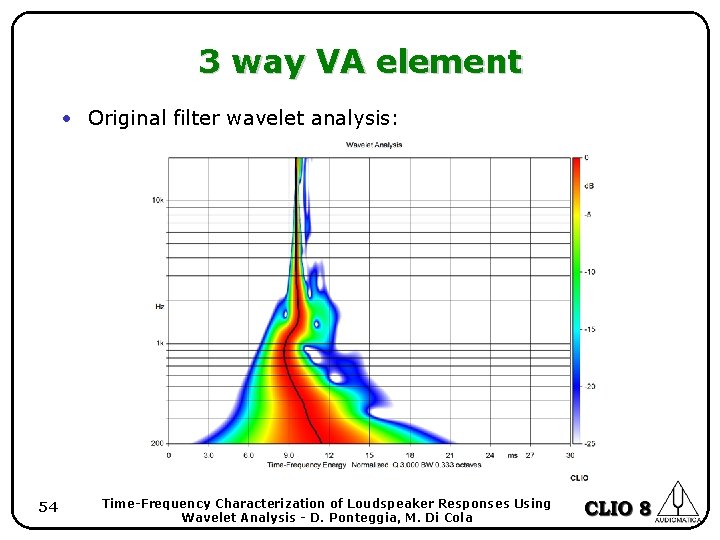
3 way VA element • Original filter wavelet analysis: 54 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

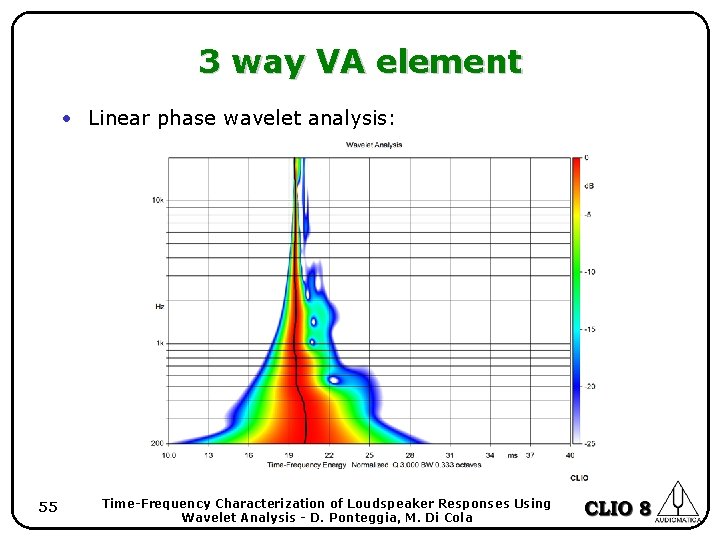
3 way VA element • Linear phase wavelet analysis: 55 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

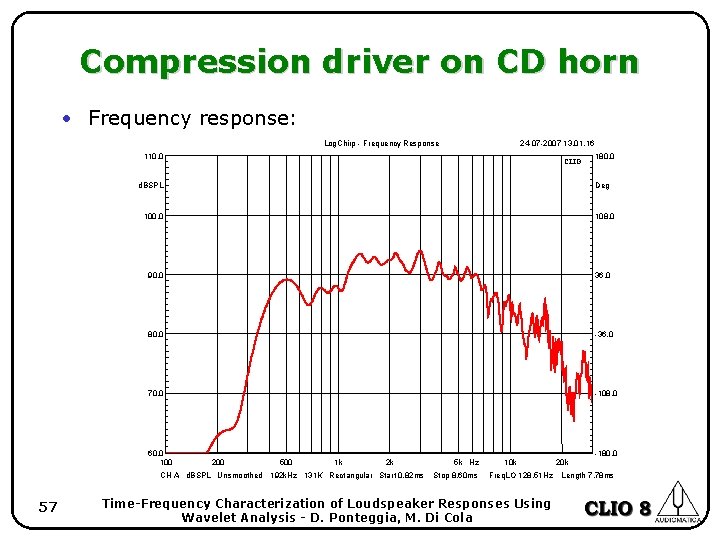
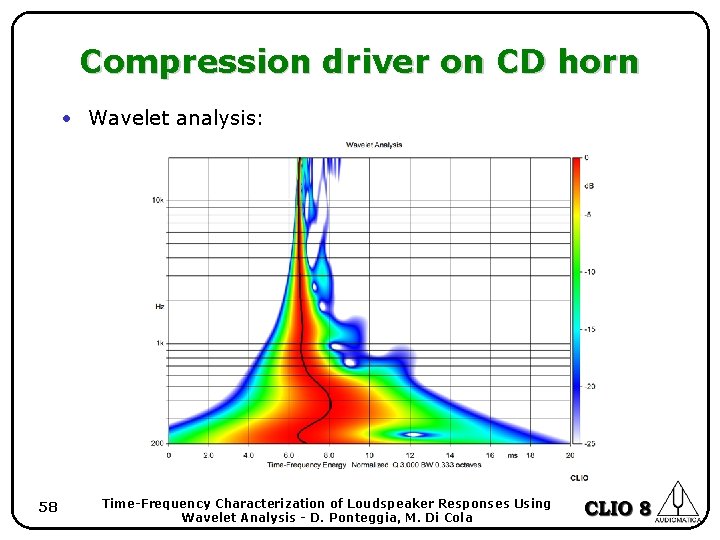
Compression driver on CD horn • A common feature of a constant directivity horn is the diffraction slot used at the horn throat. • In large format horns it is common practice to couple the drivers to an exponential portion of the horn that ends up in a very narrow slot that is forced to diffract in a subsequent section of the horn. This generates reflected waves. • The wavelet analysis can show much energy is reflected back and forward inside the horn, and which frequency bands are affected. 56 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Compression driver on CD horn • Frequency response: Log. Chirp - Frequency Response 24 -07 -2007 13. 01. 16 110. 0 CLIO d. BSPL Deg 100. 0 108. 0 90. 0 36. 0 80. 0 -36. 0 70. 0 -108. 0 60. 0 100 -180. 0 200 500 1 k 2 k CH A d. BSPL Unsmoothed 192 k. Hz 131 K Rectangular Start 0. 82 ms 57 180. 0 5 k Hz Stop 8. 60 ms 10 k Freq. LO 128. 51 Hz Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola 20 k Length 7. 78 ms

Compression driver on CD horn • Wavelet analysis: 58 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

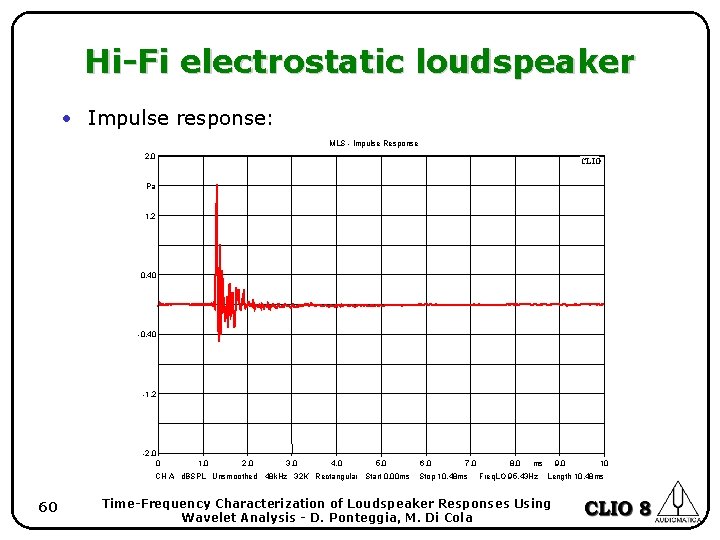
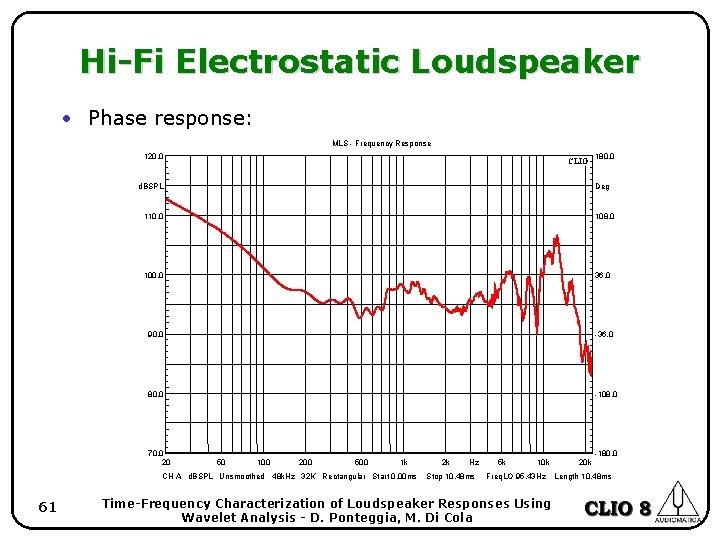
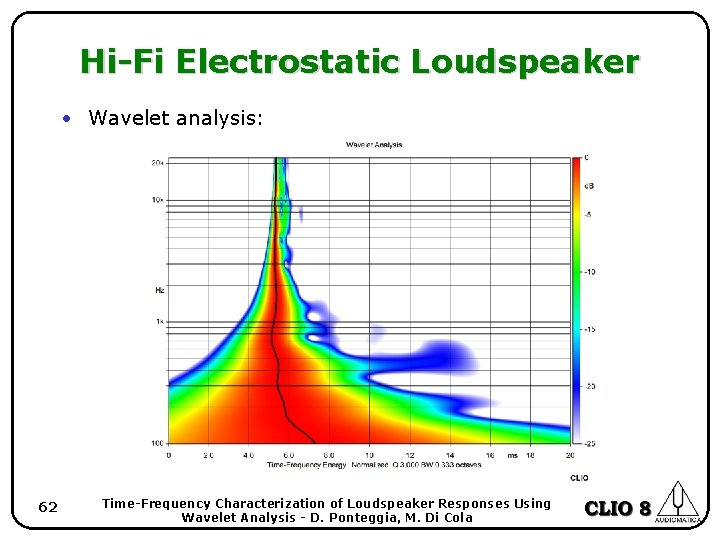
Hi-Fi electrostatic loudspeaker • We measured an HI-FI electrostatic loudspeaker that is “time aligned” by its principle of operation. • This is confirmed by the almost flat phase response. • The wavelet analysis confirm the result. 59 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Hi-Fi electrostatic loudspeaker • Impulse response: MLS - Impulse Response 2. 0 CLIO Pa 1. 2 0. 40 -1. 2 -2. 0 0 1. 0 2. 0 3. 0 4. 0 5. 0 CH A d. BSPL Unsmoothed 48 k. Hz 32 K Rectangular Start 0. 00 ms 60 6. 0 7. 0 Stop 10. 48 ms 8. 0 ms Freq. LO 95. 43 Hz 9. 0 10 Length 10. 48 ms Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Hi-Fi Electrostatic Loudspeaker • Phase response: MLS - Frequency Response 120. 0 CLIO d. BSPL Deg 110. 0 108. 0 100. 0 36. 0 90. 0 -36. 0 80. 0 -108. 0 70. 0 20 -180. 0 50 100 200 500 1 k CH A d. BSPL Unsmoothed 48 k. Hz 32 K Rectangular Start 0. 00 ms 61 180. 0 2 k Hz Stop 10. 48 ms 5 k 10 k Freq. LO 95. 43 Hz Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola 20 k Length 10. 48 ms

Hi-Fi Electrostatic Loudspeaker • Wavelet analysis: 62 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Conclusions The Wavelet Analysis: • is a useful tool to inspect loudspeaker impulse responses. • gives a system time-frequency energy footprint that is easily readable. • It could be used into the daily work of the loudspeaker or transducer designer side by side with other well-known tools. 63 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Further Developments • Enhance computational speed by using a different calculation algorithm. In the future we can move towards a “real time” wavelet analysis. • Explore alternative mappings, such as Wavelet Coefficient Phase color-maps or 3 D time-frequency-angle plots. 64 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Available Literature • O. Rioul, M. Vetterli, “Wavelets and Signal Processing” IEEE SP magazine, vol. 4, no. 4, pp. 12 -38, Oct. 1991 • D. B. Keele, “Time Frequency Display of Electroacustic Data Using Cycle-Octave Wavelet Transforms” AES 99 th, New York, NY, USA, 1995 • S. J. Loutridis, “Decomposition of Impulse Responses Using Complex Wavelets” JAES, vol. 53, No. 9, pp. 796– 811 (2005 September) • D. W. Gunness, W. R. Hoy, “A Spectrogram Display for Loudspeaker Transient Response” AES 119 th, New York, NY, USA, 2006 65 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola

Thank you for your attention! 66 Time-Frequency Characterization of Loudspeaker Responses Using Wavelet Analysis - D. Ponteggia, M. Di Cola